Le cadre de partitionnement du graphique KAHIP - Karlsruhe High Quality Partioning.
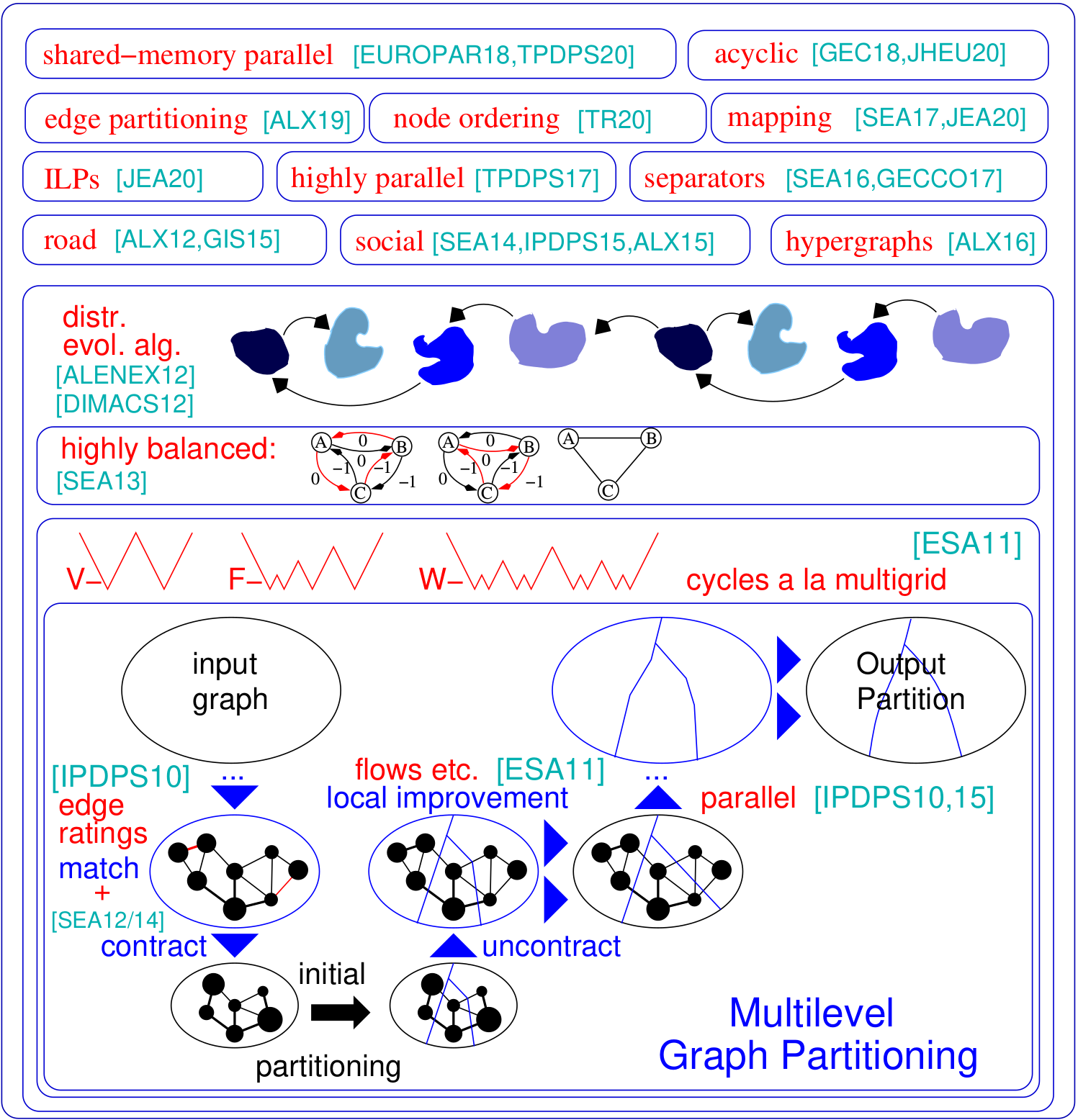
Le problème de partitionnement du graphique demande une division du nœud d'un graphique réglé dans k blocs de taille égale de telle sorte que le nombre de bords qui s'exécute entre les blocs soit minimisé. Kahip est une famille de programmes de partitionnement de graphiques. Il comprend KAFFPA (Karlsruhe Fast Flow Partioner), qui est un algorithme de partitionnement de graphiques à plusieurs niveaux, dans ses variantes fortes, Eco et Fast, Kaffpae (Kaffpaevolutionary), qui est un algorithme évolutif parallèle qui utilise KAFFPA pour associer des combinaisons et des mutations, ainsi que Kabape qui s'étend sur l'algorithme évolutionnaire. De plus, des techniques spécialisées sont incluses dans les réseaux routiers de partition (Buffoon) pour produire un séparateur de sommet d'une partition donnée ainsi que des techniques axées sur la cloison efficace des réseaux sociaux. Voici un aperçu de notre cadre:
Prise en charge de Python : Kahip peut désormais également être utilisé dans Python. Voir ci-dessous comment faire cela.
Partions hiérarchiques : Kahip peut calculer les partitions hiérarchies. Tout ce que vous avez à faire est de spécifier la hiérarchie et Kahip est prêt à partir et fait la multisection comme vous le spécifiez.
Algorithmes de commande de nœuds : de nombreuses applications reposent sur des opérations de matrice à forte intensité de temps, telles que la factorisation, qui peuvent être considérablement accélérées pour de grandes matrices clairsemées en interprétant la matrice comme un graphique clairsemé et en calculant une commande de nœud qui minimise le remplissage dite. Ici, nous avons ajouté de nouveaux algorithmes pour calculer le remplissage des commandes réduites dans les graphiques.
Les ILP pour une qualité encore de meilleure qualité : les ILP ne sont généralement pas évolutifs à de grandes cas. Nous les adaptons à améliorer heuristiquement une partition donnée. Nous le faisons en définissant un modèle beaucoup plus petit qui nous permet d'utiliser la rupture de symétrie et d'autres techniques qui rendent l'approche évolutive. Nous incluons les ILP qui peuvent être utilisés comme étape de post-traitement pour améliorer encore plus les partitions de haute qualité. Les codes sont désormais inclus dans Kahip.
TCMALLOC: Nous avons ajouté la possibilité de lier à TCMalloc. Selon votre système, cela peut produire un algorithme global plus rapide car il fournit des opérations Malloc plus rapides.
IO plus rapide : nous avons ajouté une option à KAFFPA (option - mmap_io) qui accélère considérablement l'EI des fichiers texte - parfois par ordre de grandeur.
Ajout du support pour les poids de vertex et de bord en paroissine : nous avons étendu la fonctionnalité IO de la parhars pour lire les graphiques pondérés au format Métis.
Mappage mondial multisection : nous avons ajouté des algorithmes globaux de mappage de processus N à 1 multisection. Cela calcule une meilleure cartographie de processus pour les applications parallèles si des informations sur la hiérarchie / architecture du système sont connues.
Déterminisme en parhars : nous avons ajouté une option pour exécuter de manière déterministe, c'est-à-dire que deux séries de parhars en utilisant la même graine rendront toujours le même résultat.
Flag de version : nous avons ajouté une option pour publier la version que vous utilisez actuellement, utilisez l'option - Version des programmes.
Parhip (partitionnement parallèle de haute qualité): Nos techniques de partitionnement parallèle de mémoire distribuée sont conçues pour partitionner des réseaux structurés hiérarchiquement tels que les graphiques Web ou les réseaux sociaux.
Algorithmes de cartographie: nos nouveaux algorithmes pour cartographier les blocs sur les processeurs pour minimiser le temps de communication global en fonction des partitions hiérarchiques du graphique de la tâche et des algorithmes de recherche locaux rapides.
Algorithmes de partitionnement des bords: nos nouveaux algorithmes pour calculer les partitions de bords des graphiques.
https://kahip.github.io
Vous pouvez télécharger Kahip avec la ligne de commande suivante:
git clone https://github.com/KaHIP/KaHIP Avant de pouvoir commencer, vous devez installer les packages logiciels suivants:
Une fois que vous avez installé les packages, tapez simplement
./compile_withcmake.sh Dans ce cas, tous les binaires, bibliothèques et en-têtes sont dans le dossier ./deploy/
Notez que ce script détecte la quantité de cœurs disponibles sur votre machine et les utilise tous pour le processus de compilation. Si vous ne voulez pas cela, définissez les NCORES variables sur le nombre de cœurs que vous souhaitez utiliser pour la compilation.
Alternativement, utilisez le processus de construction CMake standard:
mkdir build
cd build
cmake ../ -DCMAKE_BUILD_TYPE=Release
make
cd ..Dans ce cas, les binaires, les bibliothèques et les en-têtes se trouvent dans le dossier ./build ainsi que ./build/parallel/parallel_src/
Nous fournissons également la possibilité de lier à TCMalloc. Si vous l'avez installé, exécutez CMake avec l'option supplémentaire -Duse_tcmalloc = ON.
Par défaut, les programmes de commande de nœuds sont également compilés. Si vous avez installé METIS, le script de construction compile également un programme de commande de nœud plus rapide qui utilise des réductions avant d'appeler Metis ND. Notez que les Métis nécessitent GKLIB (https://github.com/karypislab/gklib).
Si vous utilisez l'option -DUSE_ILP = ON et que Gurobi a installé, le script de construction compile les programmes ILP pour améliorer une partition donnée ILP_IMPROVE et un solveur exact ILP_EXACT . Alternativement, vous pouvez également transmettre ces options à ./compile_withmake.sh par exemple:
./compile_withcmake -DUSE_ILP=OnNous offrons également une option pour prendre en charge les bords 64 bits. Pour l'utiliser, compilez Kahip avec l'option -d64bitMode = on.
Enfin, nous offrons une option pour le déterminisme en parhars, par exemple, deux courses avec la même graine vous donnera le même résultat. Notez cependant que cette option peut réduire la qualité des partitions, car les algorithmes de partitionnement initiaux n'utilisent pas d'algorithmes mémétiques sophistiqués, mais uniquement des algorithmes à plusieurs niveaux pour calculer les partitions initiales. N'utilisez cette option que si vous utilisez la parhars comme un outil. N'utilisez pas cette option si vous souhaitez faire des comparaisons de qualité avec la parhariat. Pour utiliser cette option, exécutez
./compile_withcmake -DDETERMINISTIC_PARHIP=OnPour une description du format de graphique (et une description étendue de tous les autres programmes), veuillez consulter le manuel. Nous donnons de courts exemples ici.
Ces programmes et configurations prennent un graphique et le partitionnent plus ou moins séquentiellement. Nous énumérons ici Kaffpa et Kaffpae (le cadre évolutif) et leurs configurations. En général, les configurations sont telles que vous pouvez investir beaucoup de temps dans la qualité de la solution à l'aide de l'algorithme Memetic. L'algorithme mémétique peut également être exécuté en parallèle en utilisant MPI. En général, plus vous investissez de temps et de ressources, mieux sera la qualité de votre partition. Nous avons beaucoup de compromis, contactez-nous si vous ne savez pas ce qui fonctionne le mieux pour votre application. Pour une description de l'algorithme, jetez un œil aux références que nous énumérons dans le manuel.
| Cas d'utilisation | Saisir | Programmes |
|---|---|---|
| Format de graphique | graphique | |
| Évaluer les partitions | évaluateur | |
| Partitionnement rapide | Maillot | Kaffpa Preconfiguration définie sur |
| Bon partitionnement | Maillot | Kaffpa Preconfiguration définie sur Eco |
| Très bon partitionnement | Maillot | Kaffpa Preconfiguration définie sur Strong |
| La plus élevée | Maillot | kaffpae, utilisez Mpirun, grand délai limite |
| Partitionnement rapide | Sociale | Kaffpa Preconfiguration définie sur fsocial |
| Bon partitionnement | Sociale | KAFFPA Preconfiguration définie sur Esocial |
| Très bon partitionnement | Sociale | KAFFPA Preconfiguration définie sur SSOCIAL |
| La plus élevée | Sociale | kaffpae, utiliser mpirun, grand délai, préconfiguration ssociale |
| Une qualité encore de meilleure qualité | kaffpae, utilisez mpirun, grand délai limite, utilisez les options --mh_enable_tabu_search, --mh_enable_kabape |
./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=strong mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4 --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE Une grande partie du projet est des algorithmes parallèles de mémoire distribués conçus pour les réseaux ayant une structure de cluster hiérarchique telle que les graphiques Web ou les réseaux sociaux. Malheureusement, les partitions de graphes parallèles précédents développées à l'origine pour des réseaux de type maillage plus réguliers ne fonctionnent pas bien pour les réseaux complexes. Ici, nous abordons ce problème en parallélisation et en adaptant la technique de propagation de l'étiquette développée à l'origine pour le regroupement de graphiques. En introduisant des contraintes de taille, la propagation de l'étiquette devient applicable à la fois pour le grossissement et la phase de raffinement du partitionnement de graphiques à plusieurs niveaux. De cette façon, nous exploitons la structure de cluster hiérarchique présente dans de nombreux réseaux complexes. Nous obtenons une qualité de très haute qualité en appliquant un algorithme évolutif très parallèle au graphique le plus grossier. Le système résultant est à la fois plus évolutif et atteint une qualité supérieure que les systèmes de pointe comme Parmetis ou Pt-Scotch.
Notre algorithme parallèle à mémoire distribuée peut lire des fichiers binaires ainsi que des fichiers de format graphique METIS standard. Les fichiers binaires sont, en général, beaucoup plus évolutifs que la lecture de fichiers texte dans des applications parallèles. La voie à suivre ici est de convertir d'abord le fichier Metis en un fichier binaire (terminant .bgf), puis de charger celui-ci.
| Cas d'utilisation | Programmes |
|---|---|
| Partitionnement parallèle | Parhip, graph2binary, graph2binary_external, boîte à outils |
| Mémoire distribuée parallèle, maillage | Parhip avec préconfigs Ecomesh, FastMesh, UltrafastMesh |
| Mémoire distribuée parallèle, social | parhioir avec des préconfigrés écosociaux, rapides, ultrafastociaux |
| Convertir les Métis en binaire | graph2binary, graph2binary_external |
| Évaluer et convertir les partitions | boîte à outils |
./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmeshLe problème du séparateur de nœud demande à partitionner l'ensemble de nœuds d'un graphique en trois ensembles A, B et S tels que la suppression de S déconnecte A et B. Nous utilisons des algorithmes de recherche locaux basés sur le flux et localisés dans un cadre à plusieurs niveaux pour calculer les séparateurs de nœuds. Kahip peut également calculer les séparateurs de nœuds. Il peut le faire avec un séparateur de nœuds standard (2 voies), mais il peut également calculer les séparateurs de nœuds K-Way.
| Cas d'utilisation | Programmes |
|---|---|
| Séparateurs à 2 voies | Node_separator |
| Séparateurs kway | Utilisez KAFFPA pour créer une partition K, puis partition_to_vertex_separator pour créer un séparateur |
./deploy/node_separator examples/rgg_n_2_15_s0.graphDes applications telles que la factorisation peuvent être considérablement accélérées pour les grandes matrices clairsemées en interprétant la matrice comme un graphique clairsemé et en calculant une commande de nœud qui minimise le soi-disant remplissage. En appliquant des règles de réduction des données nouvelles et existantes de manière exhaustive avant la dissection imbriquée, nous obtenons une qualité améliorée et en même temps, de grandes améliorations du temps d'exécution dans divers cas. Si les métis sont installés, le script de construction compile également le programme Fast_Node_Orderring, qui exécute des réductions avant d'exécuter les Metis pour calculer une commande. Les programmes sont également disponibles via la bibliothèque.
| Cas d'utilisation | Programmes |
|---|---|
| Commande de nœud | Node_orderring (avec différentes préconfigurations) |
| Commande de nœud rapide | fast_node_orderring |
./deploy/node_ordering examples/rgg_n_2_15_s0.graph ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graphLes calculs distribués centrés sur les bords sont apparus comme une technique récente pour améliorer les lacunes des algorithmes de réflexion sur le vertex sur les réseaux sans échelle. Afin d'augmenter le parallélisme sur ce modèle, le partitionnement des bords - les bords de partitionnement en blocs à peu près également de taille - est devenu une alternative au partitionnement de graphiques traditionnel (basé sur des nœuds). Nous incluons un algorithme de construction de graphes séparés parallèle et séquentiel rapide qui fournit des partitions de bord de haute qualité de haute qualité. Notre technique évolue vers les réseaux avec des milliards d'arêtes et fonctionne efficacement sur des milliers de PE.
| Cas d'utilisation | Programmes |
|---|---|
| Partitionnement de bord | Edge_Partioning, distribué_edge_parting |
./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial La cartographie des processus de communication et de topologie est une approche puissante pour réduire le temps de communication dans les applications parallèles avec des modèles de communication connus sur de grands systèmes de mémoire distribués. Nous abordons le problème en tant que problème d'attribution quadratique (QAP) et incluons des algorithmes pour construire des mappages initiaux de processus vers les processeurs ainsi que des algorithmes de recherche locaux rapides pour améliorer encore les mappages. En exploitant des hypothèses qui conservent généralement des applications et des systèmes de superordinateurs modernes tels que des modèles de communication clairsemés et des systèmes de communication organisés hiérarchiquement, nous arrivons à des algorithmes beaucoup plus puissants pour ces QAP spéciaux. Nos algorithmes de construction à plusieurs niveaux utilisent des techniques de partitionnement de graphiques parfaitement équilibrées et exploitent excessivement la hiérarchie du système de communication donné. Depuis la V3.0, nous avons inclus des algorithmes mondiaux multisection qui partagent directement le réseau d'entrée le long de la hiérarchie spécifiée pour obtenir un mappage N à 1 et ensuite appeler les algorithmes de mappage du 1 à 1 pour améliorer encore plus la cartographie.
| Cas d'utilisation | Programmes |
|---|---|
| Cartographie des réseaux de processeurs | Kaffpa, et utilisez l'option Activer_mapping avec resp. perconfigurations |
| Multisection mondiale | Global_Multisection avec resp. perconfigurations |
./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200Nous fournissons un ILP ainsi qu'un ILP pour améliorer une partition donnée. Nous étendons le voisinage du problème de combinaison pour plusieurs recherches locales en utilisant une programmation linéaire entière. Cela nous permet de trouver des combinaisons encore plus complexes et donc d'améliorer encore les solutions. Cependant, hors de la boîte, ceux des ILP pour le problème ne sont généralement pas étendus aux grandes entrées, en particulier parce que le problème de partitionnement du graphique a une très grande quantité de symétrie - étant donné une partition du graphique, chaque permutation des ID de bloc donne une solution ayant le même objectif et le même équilibre. Nous définissons un graphique beaucoup plus petit, appelé modèle, et résolvons le problème de partitionnement du graphique sur le modèle à l'optimalité par le programme linéaire entier. Outre d'autres choses, ce modèle nous permet d'utiliser la rupture de la symétrie, ce qui nous permet d'évoluer vers des entrées beaucoup plus grandes. Afin de compiler ces programmes, vous devez exécuter CMake dans le processus de construction ci-dessus comme cmake ../ -dcmake_build_type = release -Duse_ilp = on ou exécuter ./compile_withcmake -duse_ilp = on.
| Cas d'utilisation | Programmes |
|---|---|
| Solveur exact | ilp_exact |
| Amélioration via ILP | ilp_improve |
./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4 ./deploy/ilp_exact ./examples/example_weighted.graph --k 3Kahip propose également des bibliothèques et des interfaces pour relier directement les algorithmes à votre code. Nous expliquons les détails de l'interface dans le manuel. Ci-dessous, nous énumérons un exemple de programme qui relie la bibliothèque Kahip. Cet exemple peut également être trouvé dans Misc / Example_Library_Call /.
# include < iostream >
# include < sstream >
# include " kaHIP_interface.h "
int main ( int argn, char **argv) {
std::cout << " partitioning graph from the manual " << std::endl;
int n = 5 ;
int * xadj = new int [ 6 ];
xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;
int * adjncy = new int [ 12 ];
adjncy[ 0 ] = 1 ; adjncy[ 1 ] = 4 ; adjncy[ 2 ] = 0 ; adjncy[ 3 ] = 2 ; adjncy[ 4 ] = 4 ; adjncy[ 5 ] = 1 ;
adjncy[ 6 ] = 3 ; adjncy[ 7 ] = 2 ; adjncy[ 8 ] = 4 ; adjncy[ 9 ] = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ;
double imbalance = 0.03 ;
int * part = new int [n];
int edge_cut = 0 ;
int nparts = 2 ;
int * vwgt = NULL ;
int * adjcwgt = NULL ;
kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);
std::cout << " edge cut " << edge_cut << std::endl;
}Kahip peut également être utilisé dans Python. Si vous souhaitez l'utiliser dans Python First Run
python3 -m pip install pybind11
Puis courez
./compile_withcmake.sh BUILDPYTHONMODULEPour construire le modèle Python. Cela créera le module Python et mettra également un exemple CallKahipFrompython.py dans le dossier Déployer. Vous pouvez l'exécuter en tapant ce qui suit dans le dossier de déploiement:
python3 callkahipfrompython.py Notez que nous fournissons uniquement un support préliminaire, c'est-à-dire que vous devrez peut-être modifier certains chemins en python dans le fichier compile_withcmake. Un exemple peut également être trouvé ci-dessous:
import kahip ;
#build adjacency array representation of the graph
xadj = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance = 0.03
nblocks = 2
seed = 0
# set mode
#const int FAST = 0;
#const int ECO = 1;
#const int STRONG = 2;
#const int FASTSOCIAL = 3;
#const int ECOSOCIAL = 4;
#const int STRONGSOCIAL = 5;
mode = 0
edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt ,
adjncy , nblocks , imbalance ,
supress_output , seed , mode )
print ( edgecut )
print ( blocks )Le programme est autorisé sous licence MIT. Si vous publiez des résultats à l'aide de nos algorithmes, veuillez reconnaître notre travail en citant l'article suivant:
@inproceedings{sandersschulz2013,
AUTHOR = {Sanders, Peter and Schulz, Christian},
TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
SERIES = {LNCS},
PUBLISHER = {Springer},
YEAR = {2013},
VOLUME = {7933},
PAGES = {164--175}
}
Si vous utilisez notre parasage parallèle de partitionnaire, veuillez également citer l'article suivant:
@inproceedings{meyerhenkesandersschulz2017,
AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
TITLE = {{Parallel Graph Partitioning for Complex Networks}},
JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
VOLUME = {28},
NUMBER = {9},
PAGES = {2625--2638},
YEAR = {2017}
}
Si vous utilisez un algorithme de mappage, veuillez également citer l'article suivant:
@inproceedings{schulztraeff2017,
AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
VOLUME = {75},
SERIES = {LIPIcs},
PAGES = {4:1--4:15},
YEAR = {2017}
}
Si vous utilisez des algorithmes de partitionnement Edge, veuillez également citer l'article suivant:
@inproceedings{edgepartitioning2019,
AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
TITLE = {{Scalable Edge Partitioning}},
BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
PUBLISHER = {SIAM},
PAGES = {211--225},
YEAR = {2019}
}
Si vous utilisez des algorithmes de commande de nœud, veuillez également citer l'article suivant:
@article{DBLP:journals/corr/abs-2004-11315,
author = {Wolfgang Ost and
Christian Schulz and
Darren Strash},
title = {Engineering Data Reduction for Nested Dissection},
journal = {CoRR},
volume = {abs/2004.11315},
year = {2020},
url = {https://arxiv.org/abs/2004.11315},
archivePrefix = {arXiv},
eprint = {2004.11315},
timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
biburl = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
Si vous utilisez des algorithmes ILP pour améliorer une partition, veuillez également citer l'article suivant:
@inproceedings{DBLP:conf/wea/HenzingerN018,
author = {Alexandra Henzinger and
Alexander Noe and
Christian Schulz},
title = {ILP-based Local Search for Graph Partitioning},
booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
pages = {4:1--4:15},
year = {2018},
url = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
doi = {10.4230/LIPIcs.SEA.2018.4},
series = {LIPIcs},
volume = {103},
publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}
Yaroslav akhremtsev
Adil Chhabra
Marcelo Fonseca Faraj
Roland Glantz
Alexandra Henzinger
Dennis Luxen
Henning Meyerhenke
Alexander Noe
Mark Olesen
Lara OST
Ilya Safro
Peter Sanders
Hayk Sargsyan
Sebastian Schlag
Christian Schulz (mainteneur)
Daniel Seemaier
Darren Strash
Jesper Larsson Träff