Descarga de KaHIP - Descarga del código fuente KaHIP

KaHIP

C/C++

v3.17

Descargar

Kahip v3.17

El marco de partición de gráficos Kahip - Karlsruhe Partitioning de alta calidad.

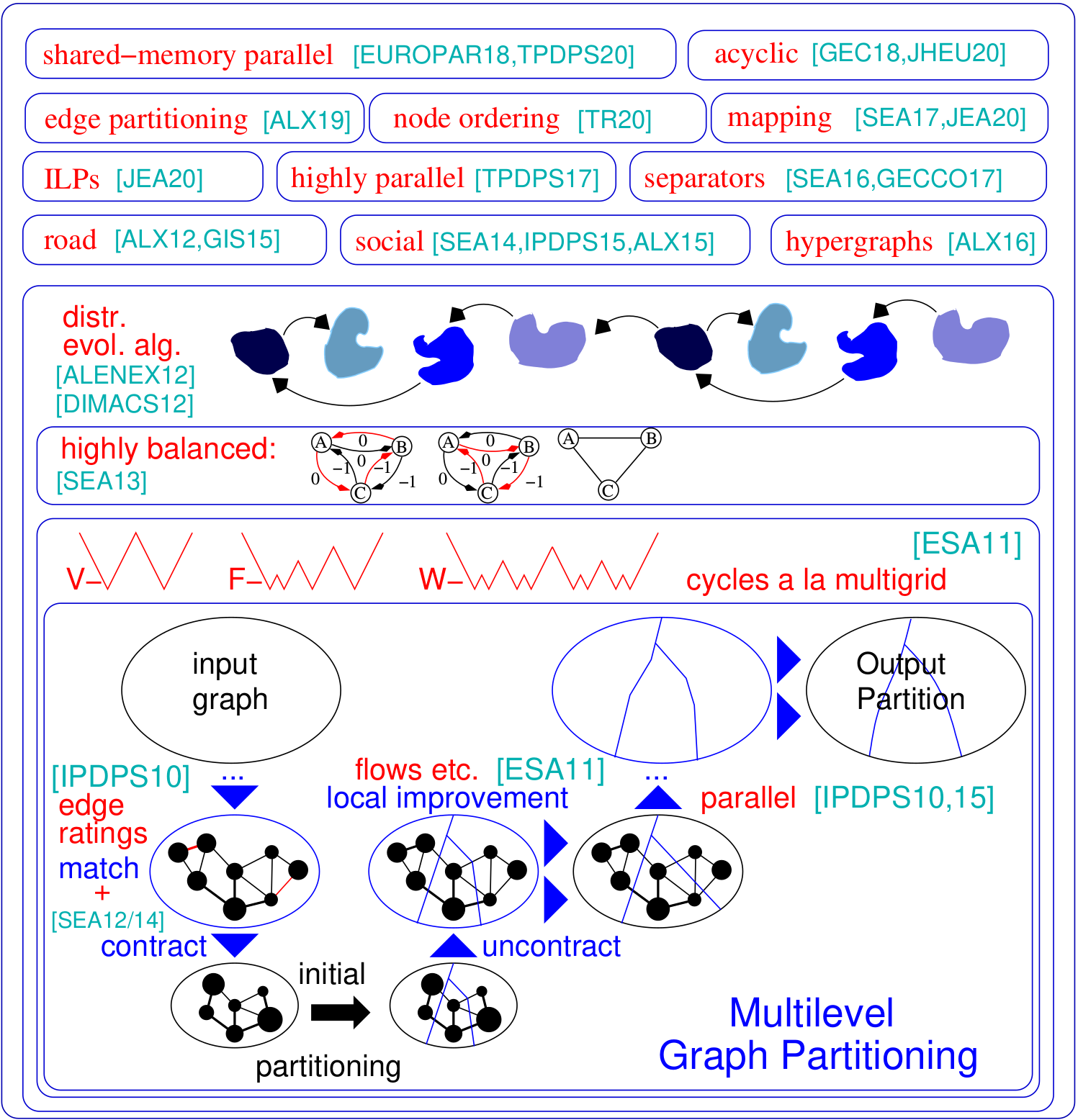
El problema de partición de gráficos solicita una división del nodo de un gráfico establecido en k bloques de tamaño igualmente de modo que se minimice el número de bordes que se ejecutan entre los bloques. Kahip es una familia de programas de partición gráfica. Incluye Kaffpa (Karlsruhe Flow Flow Particioner), que es un algoritmo de partición de gráficos multinivel, en sus variantes fuertes, ecológicas y rápidas, kaffpae (kaffpaevolutionería), que es un algoritmo evolutivo paralelo de algoritmo evolutivo para proporcionar operaciones combinadas y de mutación, así como Kabapeape, que extiende la evolutivo de la evolutiva. Además, se incluyen técnicas especializadas para dividir las redes de carreteras (bufón), para generar un separador de vértices de una partición dada, así como técnicas orientadas a la división eficiente de las redes sociales. Aquí hay una descripción general de nuestro marco:

Descripción general del marco

Nuevo en v3.14:

Soporte para Python : Kahip ahora también se puede usar en Python. Vea a continuación cómo hacer eso.

Partitaciones jerárquicas : Kahip puede calcular particiones jerárquicas. Todo lo que tiene que hacer es especificar la jerarquía y Kahip está listo para comenzar y hace la multisección como lo especificó.

Algoritmos de pedido de nodos : muchas aplicaciones se basan en operaciones de matriz intensiva en tiempo, como la factorización, que se pueden acelerar significativamente para grandes matrices dispersas al interpretar la matriz como un gráfico disperso y calcular un orden de nodo que minimiza el llamado relleno. Aquí, agregamos nuevos algoritmos para calcular los pedidos reducidos de relleno en gráficos.

Los ILP para una calidad aún más alta : los ILP generalmente no se escalan a grandes instancias. Los adaptamos a mejorar heurísticamente una partición dada. Lo hacemos definiendo un modelo mucho más pequeño que nos permite usar la ruptura de simetría y otras técnicas que hacen que el enfoque sea escalable. Incluimos ILP que pueden usarse como un paso posterior al procesamiento para mejorar aún más las particiones de alta calidad. Los códigos ahora están incluidos en Kahip.

TCMALLOC: Agregamos la posibilidad de vincular contra TCMALLOC. Dependiendo de su sistema, esto puede producir un algoritmo general más rápido, ya que proporciona operaciones de malloc más rápidas.

IO más rápido : agregamos una opción a KAFFPA (opción - -MMAP_IO) que acelera el IO de los archivos de texto significativamente, a veces por un orden de magnitud.

Se agregó soporte para el vértice y los pesos de borde en parhing : extendimos la funcionalidad IO de Parhip para leer gráficos ponderados en el formato METI.

Mapeo multisección global : agregamos algoritmos globales de mapeo de procesos N-To-1 Multisection N-To-1. Esto calcula una mejor asignación de procesos para aplicaciones paralelas si se conoce información sobre la jerarquía/arquitectura del sistema.

Determinismo en Parhip : Agregamos una opción para ejecutar parhip determinista, es decir, dos carreras de parhip usando la misma semilla siempre devolverán el mismo resultado.

Bandera de la versión : agregamos una opción para generar la versión que está utilizando actualmente, use la opción -Versión de los programas.

Nuevo en v2.10:

Parhip (partición paralela de alta calidad): nuestras técnicas de partición paralela de memoria distribuida están diseñadas para dividir redes estructuradas jerárquicamente como gráficos web o redes sociales.

Algoritmos de mapeo: nuestros nuevos algoritmos para asignar los bloques en procesadores para minimizar el tiempo general de comunicación en función de las particiones jerárquicas del gráfico de tareas y los algoritmos de búsqueda locales rápidos.

Algoritmos de partición de borde: nuestros nuevos algoritmos para calcular las particiones de gráficos de borde.

Sitio del proyecto principal:

https://kahip.github.io

Notas de instalación

Descargando kahip:

Puede descargar kahip con la siguiente línea de comando:

 git clone https://github.com/KaHIP/KaHIP

Compilando Kahip:

Antes de que pueda comenzar, debe instalar los siguientes paquetes de software:

Si desea usar algoritmos paralelos contenidos dentro del marco (por ejemplo, Parhip), necesita OpenMPI (https://www.open-mpi.org/). Si no desea ejecutar Parhip, puede deshacerse fácilmente de esta dependencia.

Una vez que haya instalado los paquetes, simplemente escriba

 ./compile_withcmake.sh

En este caso, todos los binarios, bibliotecas y encabezados están en la carpeta ./deploy/

Tenga en cuenta que este script detecta la cantidad de núcleos disponibles en su máquina y los utiliza para el proceso de compilación. Si no desea eso, establezca los NCORE variables en la cantidad de núcleos que desea usar para la compilación.

Alternativamente, use el proceso estándar de compilación de CMake:

 mkdir build
cd build 
cmake ../ -DCMAKE_BUILD_TYPE=Release     
make 
cd ..

En este caso, los binarios, bibliotecas y encabezados están en la carpeta ./build y ./build/parallel/parallel_src/

También proporcionamos la opción de vincular contra TCMALLOC. Si lo tiene instalado, ejecute cmake con la opción adicional -duse_tcmalloc = on.

Por defecto, los programas de pedido de nodos también se compilan. Si tiene instalado METI, el script de compilación también compila un programa de pedido de nodos más rápido que utiliza reducciones antes de llamar a Metis ND. Tenga en cuenta que Metis requiere GKLIB (https://github.com/karypislab/gklib).

Si usa la opción -duse_ilp = on y tiene instalado GUROBI, el script de compilación compila los programas ILP para mejorar una partición dada ILP_IMProve y un solucionador exacto ILP_EXACT . Alternativamente, también puede pasar estas opciones a ./compile_withmake.sh, por ejemplo:

 ./compile_withcmake -DUSE_ILP=On

También proporcionamos una opción para admitir los bordes de 64 bits. Para usar esto, compile kahip con la opción -d64bitmode = on.

Por último, proporcionamos una opción para el determinismo en el parhip, por ejemplo, dos corridas con la misma semilla le darán el mismo resultado. Sin embargo, tenga en cuenta que esta opción puede reducir la calidad de las particiones, ya que los algoritmos de partición iniciales no utilizan algoritmos meméticos sofisticados, sino solo algoritmos multinivel para calcular las particiones iniciales. Solo use esta opción si usa Parhip como herramienta. No use esta opción si desea hacer comparaciones de calidad contra el parhip. Para utilizar esta opción, ejecute

 ./compile_withcmake -DDETERMINISTIC_PARHIP=On

Ejecución de programas

Para obtener una descripción del formato de gráfico (y una descripción extensa de todos los demás programas), eche un vistazo al manual. Damos ejemplos cortos aquí.

Descripción general de los programas y useCase

Problema de partición predeterminado

Estos programas y configuraciones toman un gráfico y lo dividen más o menos secuencialmente. Enumeramos aquí Kaffpa y Kaffpae (el marco evolutivo) y sus configuraciones. En general, las configuraciones son tales que puede invertir mucho tiempo en la calidad de la solución utilizando el algoritmo Memetic. El algoritmo memético también se puede ejecutar en paralelo usando MPI. En general, cuanto más tiempo y recursos inviertan, mejor será la calidad de su partición. Tenemos muchas compensaciones, contáctenos si no está seguro de qué funciona mejor para su aplicación. Para obtener una descripción del algoritmo, eche un vistazo a las referencias que enumeramos en el manual.

Caso de uso	Aporte	Programas
Formato gráfico		Graph_checker
Evaluar particiones		evaluador
División rápida	Malla	Kaffpa Preconfiguration establecida para ayunar
Buena partición	Malla	Kaffpa Preconfiguration establecida en ECO
Muy buena partición	Malla	Kaffpa Preconfiguración establecida en Fuerte
La más alta calidad	Malla	kaffpae, use mpirun, límite de tiempo grande
División rápida	Social	KAFFPA Preconfiguración establecida en fsocial
Buena partición	Social	KAFFPA Preconfiguración establecida en Esocial
Muy buena partición	Social	Preconfiguración de KAFFPA establecida en SSOCIAL
La más alta calidad	Social	kaffpae, use mpirun, límite de tiempo grande, preconfiguración ssocial
Calidad aún mayor		kaffpae, use mpirun, límite de tiempo grande, use las opciones - -mh_enable_tabu_search, --mh_enable_kabape

Ejemplo de ejecución

 ./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph

 ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4  --preconfiguration=strong

 mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4  --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE

Partición paralela de memoria distribuida

Una gran parte del proyecto son los algoritmos paralelos de memoria distribuida diseñados para redes que tienen una estructura jerárquica de clúster, como gráficos web o redes sociales. Desafortunadamente, los partitores de gráficos paralelos anteriores desarrollados originalmente para redes más regulares similares a la malla no funcionan bien para redes complejas. Aquí abordamos este problema paralelizando y adaptando la técnica de propagación de etiquetas desarrollada originalmente para la agrupación de gráficos. Al introducir restricciones de tamaño, la propagación de la etiqueta se vuelve aplicable tanto para el engrosamiento como para la fase de refinamiento de la partición de gráficos multinivel. De esta manera, explotamos la estructura del clúster jerárquico presente en muchas redes complejas. Obtuvimos muy alta calidad aplicando un algoritmo evolutivo altamente paralelo al gráfico más grueso. El sistema resultante es más escalable y logra una calidad más alta que los sistemas de última generación como Parmetis o PT-scotch.

Nuestro algoritmo paralelo de memoria distribuida puede leer archivos binarios, así como archivos de formato de gráfico Metis estándar. Los archivos binarios son, en general, mucho más escalables que leer archivos de texto en aplicaciones paralelas. El camino a seguir aquí es convertir el archivo Metis en un archivo binario primero (finalización .bgf) y luego cargar este.

Caso de uso	Programas
División paralela	Parhip, Graph2Binary, Graph2Binary_External, Toolbox
Memoria distribuida paralela, malla	Parhip con preconfigs Ecomesh, FastMesh, UltrafastMesh
Memoria distribuida paralela, social	Parhip con preconfigs ecosocial, fastsocial, ultrafastsocial
Convertir metis a binario	Graph2Binary, Graph2Binary_External
Evaluar y convertir particiones	caja de instrumento

Ejemplo de ejecución

 ./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmesh

Separadores de nodos

El problema del separador del nodo solicita dividir el conjunto de nodos de un gráfico en tres conjuntos A, B y S de modo que la eliminación de S se desconexine A y B. Utilizamos algoritmos de búsqueda locales basados en flujo y localizados dentro de un marco multinivel para calcular los separadores de nodos. Kahip también puede calcular los separadores de nodos. Puede hacerlo con un separador de nodo estándar (2 vías), pero también puede calcular los separadores de nodo K-Way.

Caso de uso	Programas
Separadores de 2 vías	nodo_separador
Separadores de kway	Use kaffpa para crear K-partition, luego partition_to_vertex_separator para crear un separador

Ejemplo de ejecución

 ./deploy/node_separator examples/rgg_n_2_15_s0.graph

Orden de nodo

Las aplicaciones como la factorización se pueden acelerar significativamente para grandes matrices dispersas interpretando la matriz como un gráfico disperso y calculando un orden de nodo que minimiza el llamado relleno. Al aplicar las reglas de reducción de datos nuevas y existentes exhaustivamente antes de la disección anidada, obtenemos una calidad mejorada y al mismo tiempo grandes mejoras en el tiempo de ejecución en una variedad de instancias. Si se instala METI, el script de compilación también compila el programa Fast_Node_ordering, que ejecuta reducciones antes de ejecutar METI para calcular un pedido. Los programas también están disponibles a través de la biblioteca.

Caso de uso	Programas
Orden de nodo	node_ordering (con diferentes preconfiguraciones)
Pedido de nodo rápido	Fast_node_ordering

Ejemplo de ejecución

 ./deploy/node_ordering examples/rgg_n_2_15_s0.graph

 ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graph

División de borde

Los cálculos distribuidos centrados en el borde han aparecido como una técnica reciente para mejorar las deficiencias de los algoritmos pensados-como-a-vertex en redes sin escala a gran escala. Para aumentar el paralelismo en este modelo, la partición de borde, los bordes de partición en bloques de aproximadamente el tamaño igualmente, se ha convertido en una alternativa a la partición de gráficos tradicional (basado en nodos). Incluimos un algoritmo de construcción de gráficos divididos y de conexión rápidos paralelos y secuenciales que produce particiones de borde de alta calidad de manera escalable. Nuestra técnica escala a las redes con miles de millones de bordes, y se ejecuta de manera eficiente en miles de PE.

Caso de uso	Programas
División de borde	Edge_Partitioning, Distributed_Edge_Partitioning

Ejemplo de ejecución

 ./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast

 mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial

Mapeo de procesos

La mapeo de procesos consciente de la comunicación y la topología es un enfoque poderoso para reducir el tiempo de comunicación en aplicaciones paralelas con patrones de comunicación conocidos en grandes sistemas de memoria distribuida. Abordamos el problema como un problema de asignación cuadrática (QAP) e incluimos algoritmos para construir asignaciones iniciales de procesos a procesadores, así como algoritmos de búsqueda locales rápidos para mejorar aún más las asignaciones. Al explotar suposiciones que generalmente se mantienen para aplicaciones y sistemas de supercomputador modernos, como patrones de comunicación dispersos y sistemas de comunicación organizados jerárquicamente, llegamos a algoritmos significativamente más potentes para estos QAP especiales. Nuestros algoritmos de construcción multinivel emplean técnicas de partición gráfica perfectamente equilibradas y explotan excesivamente la jerarquía del sistema de comunicación dada. Desde V3.0 incluimos algoritmos globales de multisección que dividen directamente la red de entrada a lo largo de la jerarquía especificada para obtener un mapeo N-a-1 y luego llamar a algoritmos de mapeo 1 a 1 para mejorar aún más el mapeo.

Caso de uso	Programas
Mapeo a las redes de procesadores	KAFFPA, y use la opción Habilitar_Mapping con resp. perconfiguraciones
Multisección global	global_multisection con resp. perconfiguraciones

Ejemplo de ejecución

 ./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100

 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco  --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200

Mejoras de ILP (solucionador exacto) e ILP

Proporcionamos un ILP y un ILP para mejorar una partición dada. Extendemos el vecindario del problema de combinación para múltiples búsquedas locales empleando programación lineal entera. Esto nos permite encontrar combinaciones aún más complejas y, por lo tanto, mejorar aún más las soluciones. Sin embargo, fuera de la caja, aquellos que los ILP para el problema generalmente no escalan a grandes entradas, en particular porque el problema de partición de gráficos tiene una gran cantidad de simetría, dada una partición del gráfico, cada permutación de los ID de bloque da una solución que tiene el mismo objetivo y equilibrio. Definimos un gráfico mucho más pequeño, llamado modelo, y resolvemos el problema de partición de gráficos en el modelo a la optimización del programa lineal entero. Además de otras cosas, este modelo nos permite usar la ruptura de simetría, lo que nos permite escalar a entradas mucho más grandes. Para compilar estos programas, debe ejecutar CMake en el proceso de compilación anterior como cmake ../ -dcmake_build_type = libe -duse_ilp = en o ejecutar ./compile_withcmake -duse_ilp = on.

Caso de uso	Programas
Solucionador exacto	ILP_EXACT
Mejora a través de ILP	ILP_improve

Ejemplo de ejecución

 ./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4

 ./deploy/ilp_exact ./examples/example_weighted.graph  --k 3

Vinculando la biblioteca Kahip

Kahip también ofrece bibliotecas e interfaces para vincular los algoritmos directamente a su código. Explicamos los detalles de la interfaz en el manual. A continuación enumeramos un programa de ejemplo que vincula la Biblioteca Kahip. Este ejemplo también se puede encontrar en MISC/Ejemplo_Library_Call/.

# include < iostream >
# include < sstream >

# include " kaHIP_interface.h "


int main ( int argn, char **argv) {

        std::cout <<  " partitioning graph from the manual "  << std::endl;

        int n            = 5 ;
        int * xadj        = new int [ 6 ];
        xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;

        int * adjncy      = new int [ 12 ];
        adjncy[ 0 ]  = 1 ; adjncy[ 1 ]  = 4 ; adjncy[ 2 ]  = 0 ; adjncy[ 3 ]  = 2 ; adjncy[ 4 ]  = 4 ; adjncy[ 5 ]  = 1 ; 
        adjncy[ 6 ]  = 3 ; adjncy[ 7 ]  = 2 ; adjncy[ 8 ]  = 4 ; adjncy[ 9 ]  = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ; 
        
        double imbalance = 0.03 ;
        int * part        = new int [n];
        int edge_cut     = 0 ;
        int nparts       = 2 ;
        int * vwgt        = NULL ;
        int * adjcwgt     = NULL ;

        kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);

        std::cout <<  " edge cut " <<  edge_cut  << std::endl;
}

Usando Kahip en Python

Kahip también se puede usar en Python. Si quieres usarlo en Python First Run

 python3 -m pip install pybind11

Luego corre

 ./compile_withcmake.sh BUILDPYTHONMODULE

Para construir el modelo Python. Esto construirá el módulo Python y también pondrá un ejemplo de Callkahipfrompython.py en la carpeta de implementación. Puede ejecutar esto escribiendo lo siguiente en la carpeta de implementación:

 python3 callkahipfrompython.py

Tenga en cuenta que solo proporcionamos soporte preliminar, es decir, es posible que deba cambiar algunas rutas a Python dentro del archivo compile_withcmake. Un ejemplo también se puede encontrar a continuación:

 import kahip ;

#build adjacency array representation of the graph
xadj           = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy         = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt           = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt        = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance      = 0.03
nblocks        = 2 
seed           = 0

# set mode 
#const int FAST           = 0;
#const int ECO            = 1;
#const int STRONG         = 2;
#const int FASTSOCIAL     = 3;
#const int ECOSOCIAL      = 4;
#const int STRONGSOCIAL   = 5;
mode = 0 

edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt , 
                              adjncy ,  nblocks , imbalance , 
                              supress_output , seed , mode )

print ( edgecut )
print ( blocks )

Licencia

El programa tiene licencia bajo la licencia MIT. Si publica resultados utilizando nuestros algoritmos, reconozca nuestro trabajo citando el siguiente documento:

 @inproceedings{sandersschulz2013,
             AUTHOR = {Sanders, Peter and Schulz, Christian},
             TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
             BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
             SERIES = {LNCS},
             PUBLISHER = {Springer},
             YEAR = {2013},
             VOLUME = {7933},
             PAGES = {164--175}
}

Si usa nuestro Parhip Parallel Parhip, también cita el siguiente documento:

 @inproceedings{meyerhenkesandersschulz2017,
             AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
             TITLE = {{Parallel Graph Partitioning for Complex Networks}},
             JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
             VOLUME = {28},
             NUMBER = {9},
             PAGES = {2625--2638},
             YEAR = {2017}
}

Si usa algoritmo de mapeo, también cita el siguiente documento:

 @inproceedings{schulztraeff2017,
             AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
             TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
             BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
             PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
             VOLUME = {75},
             SERIES = {LIPIcs},
             PAGES = {4:1--4:15},
             YEAR = {2017}
}

Si usa algoritmos de partición de borde, también cita el siguiente documento:

 @inproceedings{edgepartitioning2019,
             AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
             TITLE = {{Scalable Edge Partitioning}},
             BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
             PUBLISHER = {SIAM},
             PAGES = {211--225},
             YEAR = {2019}
}

Si usa algoritmos de pedido de nodos, también cita el siguiente documento:

 @article{DBLP:journals/corr/abs-2004-11315,
  author    = {Wolfgang Ost and
               Christian Schulz and
               Darren Strash},
  title     = {Engineering Data Reduction for Nested Dissection},
  journal   = {CoRR},
  volume    = {abs/2004.11315},
  year      = {2020},
  url       = {https://arxiv.org/abs/2004.11315},
  archivePrefix = {arXiv},
  eprint    = {2004.11315},
  timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
  biburl    = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}

Si usa algoritmos ILP para mejorar una partición, también cita el siguiente documento:

 @inproceedings{DBLP:conf/wea/HenzingerN018,
  author    = {Alexandra Henzinger and
               Alexander Noe and
               Christian Schulz},
  title     = {ILP-based Local Search for Graph Partitioning},
  booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
  pages     = {4:1--4:15},
  year      = {2018},
  url       = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
  doi       = {10.4230/LIPIcs.SEA.2018.4},
  series    = {LIPIcs},
  volume    = {103},
  publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}