图形分区框架Kahip -Karlsruhe高质量分区。
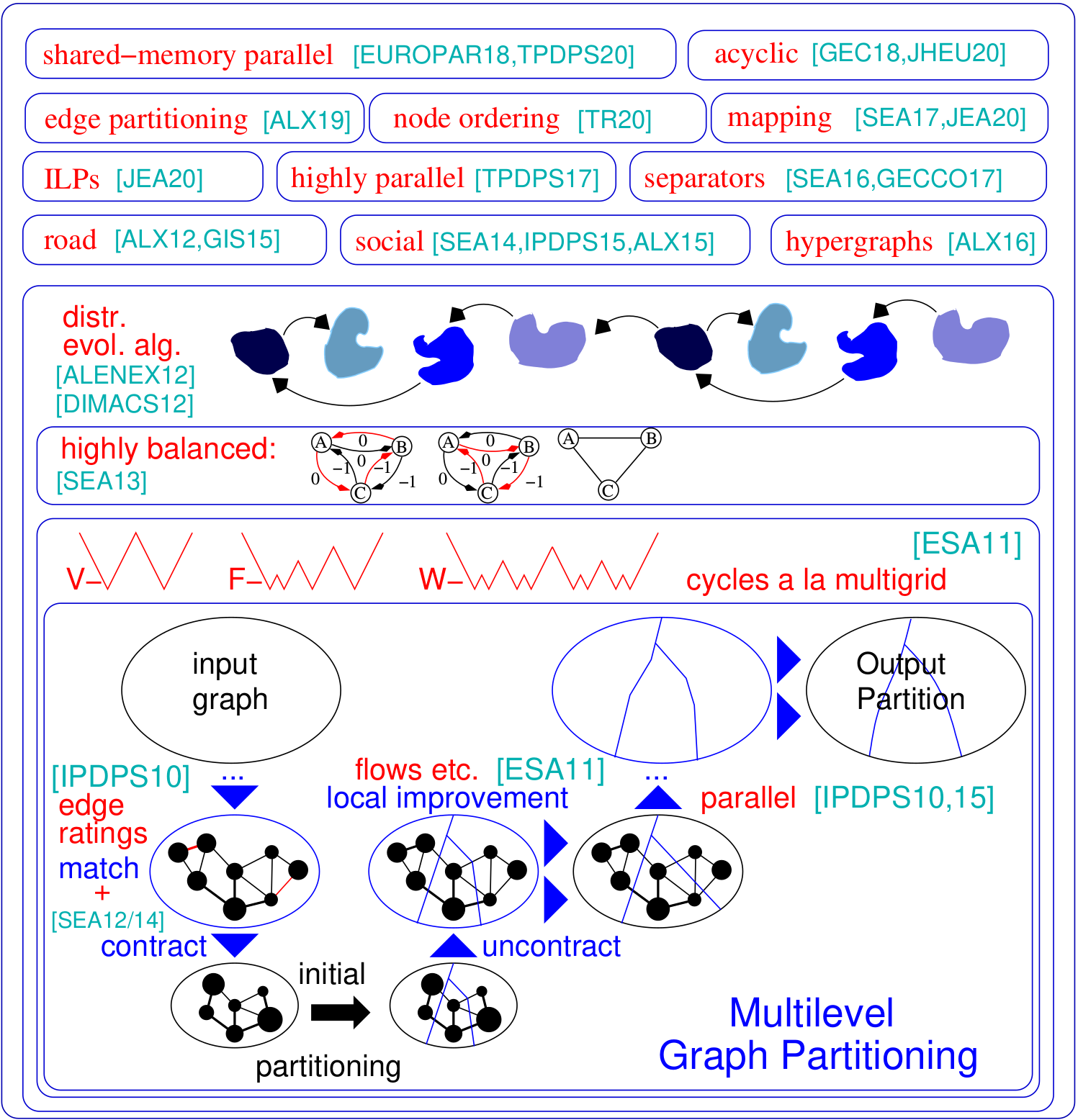
图形分区问题要求将图的节点设置为相等大小的块,以便最小化块之间运行的边数。 Kahip是图形分区程序的家族。 It includes KaFFPa (Karlsruhe Fast Flow Partitioner), which is a multilevel graph partitioning algorithm, in its variants Strong, Eco and Fast, KaFFPaE (KaFFPaEvolutionary), which is a parallel evolutionary algorithm that uses KaFFPa to provide combine and mutation operations, as well as KaBaPE which extends the evolutionary algorithm.此外,分区道路网络(Buffoon)包括专门技术,以从给定分区输出顶点分离器以及针对有效分区社交网络的技术。这是我们框架的概述:
对Python的支持:Kahip现在也可以在Python中使用。请参阅下面的方法。
分层分区:Kahip可以计算层次分区。您所要做的就是指定层次结构,而kahip可以按照指定的方式进行多个。
节点排序算法:许多应用程序依赖于时间密集型矩阵操作(例如分解),可以通过将矩阵解释为稀疏图并计算出最小化所谓的填充的节点订购来显着加速大型稀疏矩阵。在这里,我们添加了新的算法来计算图中填充的减少订单。
ILP的质量更高:ILP通常不会扩展到大型实例。我们适应它们以启发性改进给定的分区。我们通过定义一个较小的模型来做到这一点,该模型允许我们使用对称性破坏和其他使该方法可扩展的技术。我们包括可以用作后处理步骤,以进一步改善高质量分区。这些代码现在包含在Kahip中。
TCMALLOC:我们添加了针对TCMalloc链接的可能性。根据您的系统,这可以产生总体更快的算法,因为它提供了更快的Malloc操作。
更快的IO :我们在KAFFPA(选项-MMAP_IO)中添加了一个选项,该选项会大大加快文本文件的IO - 有时是按数量级的。
对顶端的顶点和边缘权重的添加了支持:我们扩展了Parhip的IO功能,以读取METIS格式的加权图。
全局多映射映射:我们添加了全局的跨度n-to Process映射算法。如果已知有关系统层次结构/体系结构的信息,则该计算并行应用程序的更好的过程映射。
Parhip中的确定性:我们添加了一个选择以确定性运行的选项,即使用相同种子的两次销售将始终返回相同的结果。
版本标志:我们添加了一个选项,以输出您当前使用的版本,请使用程序的 - Version选项。
PARHIP(并行高质量分区):我们的分布式内存并行分区技术旨在分区层次结构化的网络,例如Web图或社交网络。
映射算法:我们的新算法将块映射到处理器上,以根据任务图和快速本地搜索算法的层次分区最小化整体通信时间。
边缘分区算法:我们的新算法来计算图形的边缘分区。
https://kahip.github.io
您可以使用以下命令行下载Kahip:
git clone https://github.com/KaHIP/KaHIP 在开始之前,您需要安装以下软件包:
安装软件包后,只需键入
./compile_withcmake.sh 在这种情况下,所有二进制文件,库和标题都位于文件夹中./deploy/
请注意,此脚本检测到机器上可用的内核数量,并将所有这些内核用于编译过程。如果您不想要它,请将变量ncores设置为要用于编译的内核数。
或者使用标准CMAKE构建过程:
mkdir build
cd build
cmake ../ -DCMAKE_BUILD_TYPE=Release
make
cd ..在这种情况下,二进制文件,库和标题在文件夹中。
我们还提供了针对TCMalloc链接的选项。如果安装了它,请运行其他选项-DUSE_TCMALLOC = ON。
默认情况下,还编制了节点订购程序。如果已安装了METIS,则构建脚本还编译了一个更快的节点订购程序,该程序在调用Metis ND之前使用还原。请注意,Metis需要GKLIB(https://github.com/karypislab/gklib)。
如果您使用选项-duse_ilp = on并且已安装了Gurobi,则构建脚本会编译ILP程序以改进给定的分区ILP_IMPROVE和精确的求解器ILP_EXACT 。另外,您也可以将这些选项传递给./compile_withmake.sh:例如:
./compile_withcmake -DUSE_ILP=On我们还提供了支持64位边缘的选项。为了使用此功能,请与选项-d64bitmode = ON一起编译Kahip。
最后,我们提供了一种决定性决定性的选择,例如,具有相同种子的两次运行将为您带来相同的结果。但是请注意,此选项可以降低分区的质量,因为初始分区算法不使用复杂的模因算法,而仅使用多级算法来计算初始分区。仅在使用Parhip作为工具时才使用此选项。如果您想对Parhip进行质量比较,请勿使用此选项。要使用此选项,请运行
./compile_withcmake -DDETERMINISTIC_PARHIP=On有关图形格式的描述(以及所有其他程序的大量描述),请查看手册。我们在这里举一个简短的例子。
这些程序和配置绘制图形并或多或少地对其进行了划分。我们在这里列出Kaffpa和Kaffpae(进化框架)及其配置。通常,配置使您可以使用模因算法将大量时间投入到解决方案质量上。模因算法也可以使用MPI并行运行。通常,您投资的时间和资源越多,分区的质量就越好。我们有很多权衡,如果您不确定哪种最适合您的应用程序,请与我们联系。有关算法的描述,请查看我们在手册中列出的参考文献。
| 用例 | 输入 | 程序 |
|---|---|---|
| 图格式 | graph_checker | |
| 评估分区 | 评估员 | |
| 快速分区 | 网眼 | KAFFPA预配置设置为快速 |
| 良好的分区 | 网眼 | KAFFPA预配置设置为ECO |
| 很好的分区 | 网眼 | KAFFPA预配置设置为强 |
| 最高质量 | 网眼 | kaffpae,使用Mpirun,较大的时间限制 |
| 快速分区 | 社会的 | KAFFPA预配置设置为Fsocial |
| 良好的分区 | 社会的 | KAFFPA预配置设置为社交 |
| 很好的分区 | 社会的 | KAFFPA预配置设置为社交 |
| 最高质量 | 社会的 | Kaffpae,使用Mpirun,较大的时间限制,预配置SSSOCIAL |
| 甚至更高的质量 | kaffpae,使用Mpirun,较大的时间限制,使用选项-mh_enable_tabu_search,-mh_enable_kabape |
./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=strong mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4 --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE 该项目的很大一部分是为具有层次群集结构(例如Web图或社交网络)的网络设计的分布式内存并行算法。不幸的是,最初针对更常规网络的网络开发的先前的并行图分区器对于复杂的网络无法很好地工作。在这里,我们通过并行化和适应最初用于图形聚类的标签传播技术来解决此问题。通过引入尺寸约束,标签传播适用于多级图分区的粗化和改进阶段。这样,我们利用许多复杂网络中存在的分层群集结构。我们通过将高度平行的进化算法应用于最高图来获得很高的质量。与Parmetis或Pt-Scotch这样的最先进的系统相比,所得系统更可扩展和更高的质量。
我们的分布式存储器并行算法可以读取二进制文件以及标准的METIS图格式文件。通常,二进制文件比在并行应用程序中读取文本文件更具扩展性。到此为止的方法是首先将METIS文件转换为二进制文件(Ending .BGF),然后加载该文件。
| 用例 | 程序 |
|---|---|
| 并行分区 | Parhip,Graph2Binary,Graph2Binary_external,工具箱 |
| 分布式存储器平行于网格 | 与Preponfigs ecomesh,FastMesh,UltrafastMesh的托管 |
| 分布式记忆平行于社交 | 与预感的生态社会,快速社会,超级社会 |
| 将梅蒂斯转换为二进制 | graph2binary,graph2binary_external |
| 评估和转换分区 | 工具箱 |
./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmesh节点分离器问题要求将图的节点集划分为三组A,B和S,以使S离断开A和B。我们使用基于流量的和局部的本地搜索算法在多级别的框架内使用基于流量的本地搜索算法来计算节点分离器。 Kahip还可以计算节点分离器。它可以使用标准节点分离器(2向)进行操作,但也可以计算K-Way节点分离器。
| 用例 | 程序 |
|---|---|
| 2向分离器 | node_separator |
| Kway分离器 | 使用kaffpa创建k部分,然后使用partition_to_vertex_separator创建一个分隔符 |
./deploy/node_separator examples/rgg_n_2_15_s0.graph可以通过将矩阵解释为稀疏图并计算最小化所谓的填充的节点排序来显着加强诸如分解诸如分解之类的应用。通过在嵌套解剖之前详尽地应用新的和现有的数据减少规则,我们可以提高质量,同时在各种实例上的运行时间进行大量改进。如果安装了METIS,则构建脚本还编译了FAST_NODE_ORDERING程序,该程序在运行METIS之前运行还原以计算订购。该程序也可以通过库获得。
| 用例 | 程序 |
|---|---|
| 节点排序 | node_ordering(具有不同的预配置) |
| 快速节点排序 | fast_node_ordering |
./deploy/node_ordering examples/rgg_n_2_15_s0.graph ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graph以边缘为中心的分布式计算是一种最新技术,可以改善大型无规模网络上的Think-A-vertex算法的缺点。为了增加此模型上的并行性,边缘分区(将边缘分配到大小相同的块中)已成为传统(基于节点)图分区的替代方法。我们包括一种快速的平行和顺序分开的图形结构算法,该算法以可扩展的方式产生高质量的边缘分区。我们的技术扩展到具有数十亿个边缘的网络,并在数千个PE上有效地运行。
| 用例 | 程序 |
|---|---|
| 边缘分区 | edge_partixing,distribute_edge_partionting |
./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial 通信和拓扑意识过程映射是一种有力的方法,可以在具有大型分布式内存系统上具有已知通信模式的并行应用中减少通信时间。我们将问题作为二次分配问题(QAP)解决,并包括算法以构建流程对处理器的初始映射以及快速的本地搜索算法,以进一步改善映射。通过利用通常适用于应用程序和现代超级计算机系统(例如稀疏通信模式和层次组织的通信系统)的假设,我们为这些特殊QAPS提供了更强大的算法。我们的多级构造算法采用完美平衡的图形分区技术,并过度利用给定的通信系统层次结构。由于v3.0,我们包括了全局多元算法,这些算法将沿指定层次结构的输入网络直接划分以获取n-to-1映射,然后调用1到1映射算法以进一步改善映射。
| 用例 | 程序 |
|---|---|
| 映射到处理器网络 | kaffpa,并使用resp使用enable_mapping选项。渗透 |
| 全球多剖面 | global_multisection with resp。渗透 |
./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200我们提供ILP和ILP来改善给定分区。我们通过采用整数线性编程来扩展组合问题的附近,以进行多个本地搜索。这使我们能够找到更复杂的组合,因此可以进一步改善解决方案。但是,开箱即用这些问题的ILP通常不会扩展到大输入,尤其是因为图形分配问题具有大量的对称性 - 鉴于图形的分区,块IDS的每个置换率都具有相同目标和平衡的解决方案。我们定义了一个较小的图形,称为模型,并将模型上的图形分区问题求解到整数线性程序的最佳性。除其他事项外,该模型使我们能够使用对称性破坏,这使我们可以扩展到更大的输入。为了编译这些程序,您需要在上面的构建过程中运行cmake。
| 用例 | 程序 |
|---|---|
| 确切的求解器 | ILP_EXACT |
| 通过ILP进行改进 | ILP_IMPROVE |
./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4 ./deploy/ilp_exact ./examples/example_weighted.graph --k 3Kahip还提供了库和接口,可以将算法直接链接到您的代码。我们解释了手册中界面的细节。在下面,我们列出了链接Kahip库的示例程序。此示例也可以在MISC/example_library_call/中找到。
# include < iostream >
# include < sstream >
# include " kaHIP_interface.h "
int main ( int argn, char **argv) {
std::cout << " partitioning graph from the manual " << std::endl;
int n = 5 ;
int * xadj = new int [ 6 ];
xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;
int * adjncy = new int [ 12 ];
adjncy[ 0 ] = 1 ; adjncy[ 1 ] = 4 ; adjncy[ 2 ] = 0 ; adjncy[ 3 ] = 2 ; adjncy[ 4 ] = 4 ; adjncy[ 5 ] = 1 ;
adjncy[ 6 ] = 3 ; adjncy[ 7 ] = 2 ; adjncy[ 8 ] = 4 ; adjncy[ 9 ] = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ;
double imbalance = 0.03 ;
int * part = new int [n];
int edge_cut = 0 ;
int nparts = 2 ;
int * vwgt = NULL ;
int * adjcwgt = NULL ;
kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);
std::cout << " edge cut " << edge_cut << std::endl;
}Kahip也可以在Python中使用。如果您想在Python首次运行中使用它
python3 -m pip install pybind11
然后运行
./compile_withcmake.sh BUILDPYTHONMODULE构建Python模型。这将构建Python模块,还将示例callkahipfrompython.py放入部署文件夹中。您可以通过在部署文件夹中键入以下内容来运行此操作:
python3 callkahipfrompython.py 请注意,我们只提供初步支持,即您可能需要将一些路径更改为compile_withcmake文件中的python。也可以在下面找到一个示例:
import kahip ;
#build adjacency array representation of the graph
xadj = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance = 0.03
nblocks = 2
seed = 0
# set mode
#const int FAST = 0;
#const int ECO = 1;
#const int STRONG = 2;
#const int FASTSOCIAL = 3;
#const int ECOSOCIAL = 4;
#const int STRONGSOCIAL = 5;
mode = 0
edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt ,
adjncy , nblocks , imbalance ,
supress_output , seed , mode )
print ( edgecut )
print ( blocks )该计划已根据MIT许可获得许可。如果您使用我们的算法发布结果,请通过引用以下论文来确认我们的工作:
@inproceedings{sandersschulz2013,
AUTHOR = {Sanders, Peter and Schulz, Christian},
TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
SERIES = {LNCS},
PUBLISHER = {Springer},
YEAR = {2013},
VOLUME = {7933},
PAGES = {164--175}
}
如果您使用我们的并行分区派托,请还引用以下论文:
@inproceedings{meyerhenkesandersschulz2017,
AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
TITLE = {{Parallel Graph Partitioning for Complex Networks}},
JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
VOLUME = {28},
NUMBER = {9},
PAGES = {2625--2638},
YEAR = {2017}
}
如果使用映射算法,请还引用以下论文:
@inproceedings{schulztraeff2017,
AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
VOLUME = {75},
SERIES = {LIPIcs},
PAGES = {4:1--4:15},
YEAR = {2017}
}
如果您使用边缘分区算法,请还引用以下论文:
@inproceedings{edgepartitioning2019,
AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
TITLE = {{Scalable Edge Partitioning}},
BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
PUBLISHER = {SIAM},
PAGES = {211--225},
YEAR = {2019}
}
如果使用节点订购算法,请还引用以下论文:
@article{DBLP:journals/corr/abs-2004-11315,
author = {Wolfgang Ost and
Christian Schulz and
Darren Strash},
title = {Engineering Data Reduction for Nested Dissection},
journal = {CoRR},
volume = {abs/2004.11315},
year = {2020},
url = {https://arxiv.org/abs/2004.11315},
archivePrefix = {arXiv},
eprint = {2004.11315},
timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
biburl = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
如果您使用ILP算法来改进分区,请同时引用以下论文:
@inproceedings{DBLP:conf/wea/HenzingerN018,
author = {Alexandra Henzinger and
Alexander Noe and
Christian Schulz},
title = {ILP-based Local Search for Graph Partitioning},
booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
pages = {4:1--4:15},
year = {2018},
url = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
doi = {10.4230/LIPIcs.SEA.2018.4},
series = {LIPIcs},
volume = {103},
publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}
Yaroslav Akhremtsev
阿迪尔·恰布拉(Adil Chhabra)
Marcelo Fonseca Faraj
罗兰·格兰兹(Roland Glantz)
亚历山德拉·亨辛格(Alexandra Henzinger)
丹尼斯·卢克森(Dennis Luxen)
Henning Meyerhenke
亚历山大·诺
马克·奥尔森
拉拉·奥斯特(Lara Ost)
Ilya Safro
彼得·桑德斯
海克·萨尔格森(Hayk Sargsyan)
塞巴斯蒂安·施拉格(Sebastian Schlag)
克里斯蒂安·舒尔茨(维护者)
丹尼尔·梅西耶(Daniel Seemaier)
达伦·斯特拉什(Darren Strash)
JesperLarssonTräff