KaHIP 다운로드 - KaHIP 소스 코드 다운로드

KaHIP

C/C++

v3.17

다운로드

카하이프 v3.17

그래프 파티셔닝 프레임 워크 Kahip -Karlsruhe 고품질 파티셔닝.

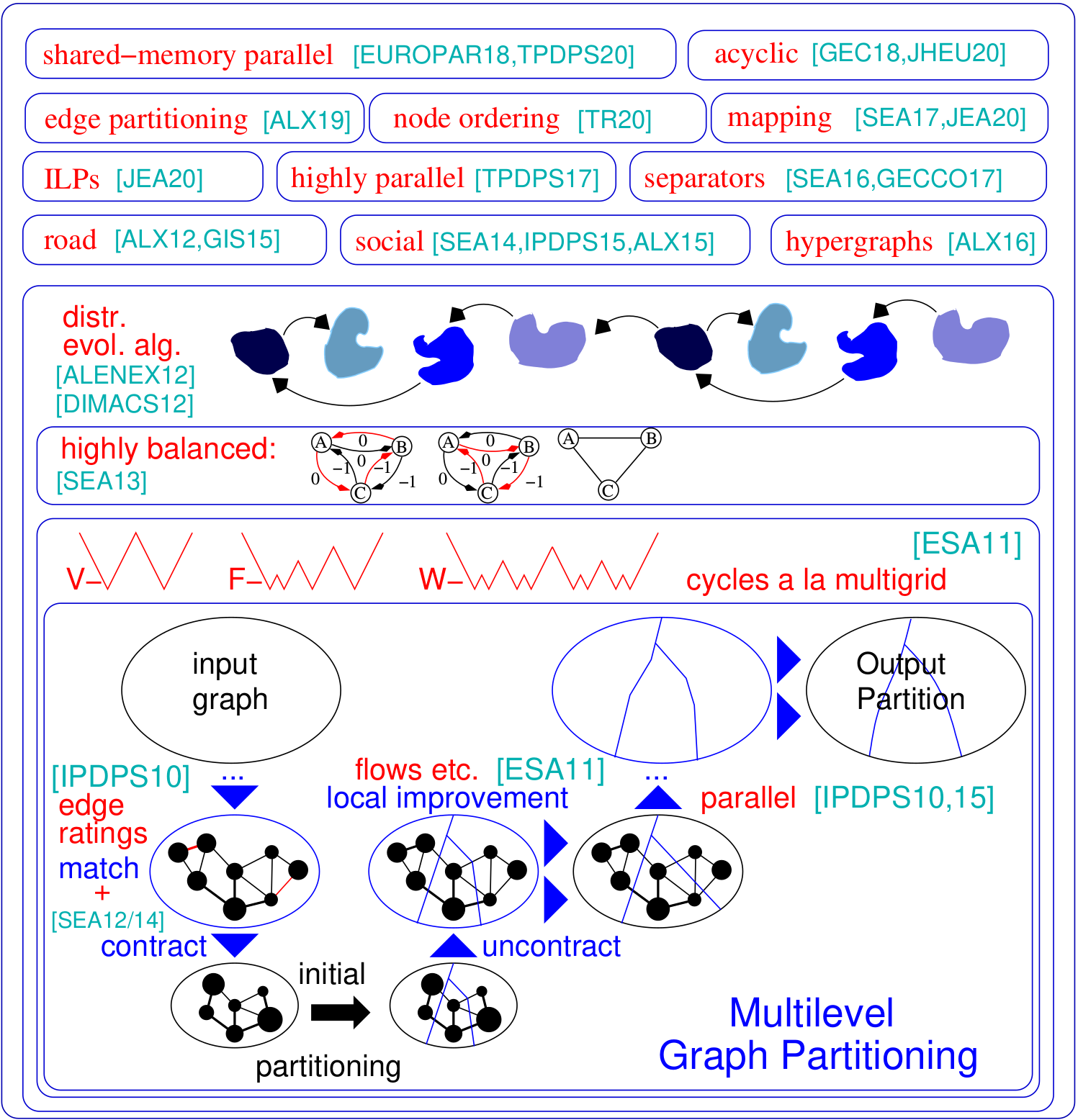
그래프 파티셔닝 문제는 블록 사이에서 실행되는 모서리 수가 최소화되도록 그래프의 노드를 k 동일 크기의 블록으로 분할해야합니다. Kahip은 그래프 파티셔닝 프로그램의 제품군입니다. 여기에는 Kaffpa (Karlsruhe Fast Flow Partitioner)가 포함되어 있으며, 이는 Kaffpa를 사용하여 콤바인 및 돌연변이 작업을 제공하는 평행 진화 알고리즘 인 kafpa를 제공하는 평행 진화 알고리즘 인 kaffa를 제공하는 평행 진화론 알고리즘 인 Kaffpae (Kaffpaevolutionary)의 다단계 그래프 파티셔닝 알고리즘입니다. 또한, 전문 기술은 Road Networks (Buffoon)에 포함되어 주어진 파티션으로부터 정점 분리기를 출력 할뿐만 아니라 소셜 네트워크의 효율적인 분할을위한 기술을 포함합니다. 다음은 프레임 워크에 대한 개요입니다.

프레임 워크 개요

v3.14의 새로운 새로운 :

파이썬에 대한 지원 : 카하이프는 이제 파이썬에서도 사용할 수 있습니다. 아래에서 아래를 참조하십시오.

계층 적 분할 : Kahip은 계층 적 분할을 계산할 수 있습니다. 계층 구조를 지정하기 만하면 Kahip이 갈 준비가되어 있으며 지정된 다중 섹션을 수행하기 만하면됩니다.

노드 순서 알고리즘 : 많은 응용 프로그램은 매트릭스를 희소 그래프로 해석하고 소위 필인을 최소화하는 노드 순서를 계산하여 큰 스파 스 유교대에 대해 크게 스파크 할 수있는 인수 분해와 같은 시간 집약적 인 매트릭스 작업에 의존합니다. 여기서는 그래프의 필인 감소 순서를 계산하기 위해 새로운 알고리즘을 추가했습니다.

더 높은 품질을위한 ILPS : ILPS는 일반적으로 큰 인스턴스로 확장되지 않습니다. 우리는 그들을 주어진 파티션을 휴리스사로 향상시키기 위해 그들을 조정합니다. 우리는 대칭 브레이킹 및 접근 방식을 확장 가능하게 만드는 다른 기술을 사용할 수있는 훨씬 작은 모델을 정의함으로써 그렇게합니다. 우리는 고품질 파티션을 더욱 향상시키기위한 후 처리 단계로 사용할 수있는 ILP를 포함합니다. 코드는 이제 kahip에 포함되어 있습니다.

TCMALLOC : 우리는 TCMALLOC에 연결할 가능성을 추가했습니다. 시스템에 따라 더 빠른 Malloc 작업을 제공하므로 전체적으로 더 빠른 알고리즘을 생성 할 수 있습니다.

더 빠른 IO : 우리는 텍스트 파일의 IO를 크게 속도로, 때로는 크기로 kaffpa (옵션 -mmap_io)에 옵션을 추가했습니다.

PARHIP의 정점 및 에지 가중치에 대한 지원 추가 : Metis 형식의 가중 그래프를 읽기 위해 Parhip의 IO 기능을 확장했습니다.

글로벌 다중 섹션 매핑 : 글로벌 다중 섹션 N-1 프로세스 매핑 알고리즘을 추가했습니다. 시스템 계층/아키텍처에 대한 정보가 알려진 경우 병렬 응용 프로그램에 대한 더 나은 프로세스 매핑을 계산합니다.

PARHIP의 결정론 : 우리는 결정적으로 구포를 실행하는 옵션을 추가했습니다. 즉, 동일한 씨앗을 사용하여 두 번의 런 런은 항상 동일한 결과를 반환합니다.

버전 플래그 : 현재 사용중인 버전을 출력하여 프로그램의 version 옵션을 사용하는 옵션을 추가했습니다.

v2.10의 새로운 새로운 :

PARIP (병렬 고품질 파티셔닝) : 분산 메모리 병렬 파티션 기술은 웹 그래프 또는 소셜 네트워크와 같은 계층 구조 네트워크를 분할하도록 설계되었습니다.

매핑 알고리즘 : 작업 그래프의 계층 적 파티셔닝 및 빠른 로컬 검색 알고리즘을 기반으로 전체 통신 시간을 최소화하기 위해 블록을 프로세서에 매핑하는 새로운 알고리즘.

Edge Partitioning 알고리즘 : 그래프의 에지 파티션을 계산하기위한 새로운 알고리즘.

주요 프로젝트 사이트 :

https://kahip.github.io

설치 노트

Kahip 다운로드 :

다음 명령 줄로 kahip을 다운로드 할 수 있습니다.

 git clone https://github.com/KaHIP/KaHIP

kahip 컴파일 :

시작하기 전에 다음 소프트웨어 패키지를 설치해야합니다.

프레임 워크 (예 : Parhip)에 포함 된 병렬 알고리즘을 사용하려면 OpenMPI (https://www.open-mpi.org/)가 필요합니다. Parhip을 실행하고 싶지 않다면이 종속성을 쉽게 제거 할 수 있습니다.

패키지를 설치 한 후에는 입력하십시오

 ./compile_withcmake.sh

이 경우 모든 바이너리, 라이브러리 및 헤더는 폴더에 있습니다 ./deploy/

이 스크립트는 컴퓨터에서 사용 가능한 코어 양을 감지하고 컴파일 프로세스에 모두 사용합니다. 원하지 않으면 변수 NCORE를 컴파일에 사용할 코어 수로 설정하십시오.

또는 표준 CMAKE 빌드 프로세스를 사용하십시오.

 mkdir build
cd build 
cmake ../ -DCMAKE_BUILD_TYPE=Release     
make 
cd ..

이 경우 바이너리, 라이브러리 및 헤더는 폴더 ./build와 ./build/parallel/parallel_src/에 있습니다.

또한 TCMALLOC에 연결하는 옵션도 제공합니다. 설치 한 경우 추가 옵션 -duse_tcmalloc = on으로 cmake를 실행하십시오.

기본적으로 노드 순서 프로그램도 컴파일됩니다. Metis가 설치된 경우 빌드 스크립트는 Metis ND를 호출하기 전에 감소를 사용하는 더 빠른 노드 순서 프로그램을 컴파일합니다. Metis에는 gklib (https://github.com/karypislab/gklib)이 필요합니다.

옵션 -duse_ilp = on을 사용하고 Gurobi가 설치된 경우 빌드 스크립트는 ILP 프로그램을 컴파일하여 주어진 파티션 ILP_IMPROVE 및 정확한 솔버 ILP_EXACT를 개선합니다. 또는 예를 들어이 옵션을 ./compile_withmake.sh로 전달할 수도 있습니다.

 ./compile_withcmake -DUSE_ILP=On

또한 64 비트 가장자리를 지원하는 옵션도 제공합니다. 이것을 사용하려면 옵션 -d64bitmode = on 옵션으로 kahip을 컴파일하십시오.

마지막으로, 우리는 Parhip에서 결정론을위한 옵션을 제공합니다. 예를 들어 동일한 씨앗을 가진 두 개의 달리기는 당신에게 동일한 결과를 줄 것입니다. 그러나 초기 파티션 알고리즘은 정교한 메틱 알고리즘을 사용하지 않고 초기 파티션을 계산하기 위해 다단계 알고리즘 만 사용하기 때문에이 옵션은 파티션의 품질을 줄일 수 있습니다. Parhip을 도구로 사용하는 경우이 옵션 만 사용하십시오. Parhip과 품질을 비교하려면이 옵션을 사용하지 마십시오. 이 옵션을 사용하려면 실행하십시오

 ./compile_withcmake -DDETERMINISTIC_PARHIP=On

실행 프로그램

그래프 형식에 대한 설명 (및 다른 모든 프로그램에 대한 광범위한 설명)은 매뉴얼을 살펴보십시오. 우리는 여기에 짧은 예를 제시합니다.

프로그램 및 usecase의 개요

기본 파티셔닝 문제

이 프로그램과 구성은 그래프를 가져 와서 다소 순차적으로 분할합니다. 우리는 여기에 Kaffpa와 Kaffpae (진화 프레임 워크)와 그 구성을 나열합니다. 일반적으로 구성은 Memetic 알고리즘을 사용하여 솔루션 품질에 많은 시간을 투자 할 수 있도록합니다. memetic 알고리즘은 MPI를 사용하여 병렬로 실행할 수 있습니다. 일반적으로 투자 시간과 자원이 많을수록 파티션의 품질이 더 좋습니다. 우리는 많은 트레이드 오프가 있습니다. 신청에 가장 적합한 것이 확실하지 않은 경우 저희에게 연락하십시오. 알고리즘에 대한 설명을 위해서는 매뉴얼에 나열된 참조를 살펴 봅니다.

유스 케이스	입력	프로그램
그래프 형식		그래프 _checker
파티션을 평가하십시오		평가자
빠른 분할	메쉬	Kaffpa 사전 구성이 빠르게 설정되었습니다
좋은 분할	메쉬	Kaffpa 사전 구성은 Eco로 설정되었습니다
아주 좋은 분할	메쉬	Kaffpa 사전 구성은 강하게 설정되었습니다
최고 품질	메쉬	Kaffpae, Mpirun, 큰 시간 제한을 사용하십시오
빠른 분할	사회의	Kaffpa 사전 구성은 fsocial로 설정되었습니다
좋은 분할	사회의	kaffpa 사전 구성은 Esocial으로 설정되었습니다
아주 좋은 분할	사회의	Kaffpa 사전 구성은 ssocial으로 설정되었습니다
최고 품질	사회의	Kaffpae, Mpirun 사용, 큰 시간 제한, 사전 구성 ssocial
훨씬 더 높은 품질		kaffpae, mpirun 사용, 큰 시간 제한, 옵션 사용 -MH_ENALE_TABU_SEARCH, ---MH_ENALE_KABAPE

예제 실행

 ./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph

 ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4  --preconfiguration=strong

 mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4  --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE

분산 메모리 병렬 파티셔닝

프로젝트의 대부분은 웹 그래프 또는 소셜 네트워크와 같은 계층 적 클러스터 구조를 갖는 네트워크를 위해 설계된 메모리 병렬 알고리즘입니다. 불행하게도, 이전의 병렬 그래프 파티셔너는 원래보다 일반적인 메시와 같은 네트워크를 위해 개발 된 복잡한 네트워크에는 적합하지 않습니다. 여기서 우리는 그래프 클러스터링을 위해 원래 개발 된 레이블 전파 기술을 병렬화하고 조정 하여이 문제를 해결합니다. 크기 제약 조건을 도입함으로써 라벨 전파는 다단계 그래프 파티셔닝의 조잡 및 정제 단계 모두에 적용됩니다. 이런 식으로 우리는 많은 복잡한 네트워크에 존재하는 계층 적 클러스터 구조를 이용합니다. 우리는 가장 평행 한 진화 알고리즘을 가장 거친 그래프에 적용하여 매우 높은 품질을 얻습니다. 결과 시스템은 Parmetis 또는 PT-Scotch와 같은 최첨단 시스템보다 더 확장 가능하며 품질이 높아집니다.

분산 메모리 병렬 알고리즘은 이진 파일과 표준 Metis 그래프 형식 파일을 읽을 수 있습니다. 이진 파일은 일반적으로 병렬 응용 프로그램에서 텍스트 파일을 읽는 것보다 훨씬 확장 가능합니다. 여기로가는 방법은 Metis 파일을 먼저 바이너리 파일로 변환 한 다음이 파일을로드하는 것입니다.

유스 케이스	프로그램
병렬 분할	PARIP, Graph2Binary, Graph2Binary_External, Toolbox
분산 메모리 평행, 메시	Preconfigs ecomesh, Fastmesh, Ultrafastmesh와의 패권
분산 메모리 평행, 소셜	생태 사회적, 빠른 사회적, 초 사회적, 초 사회적, 초 사회적, preconfigs와의 파수
Metis를 바이너리로 변환합니다	Graph2Binary, Graph2Binary_External
파티션을 평가하고 변환합니다	도구 상자

예제 실행

 ./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmesh

노드 분리기

노드 분리기 문제는 S 그래프의 노드 세트를 세트 A, B 및 S로 분할하여 S 분리 a와 B를 제거하도록 요구합니다. Kahip은 또한 노드 분리기를 계산할 수 있습니다. 표준 노드 분리기 (2 방향)로 수행 할 수 있지만 K- 웨이 노드 분리기를 계산할 수도 있습니다.

유스 케이스	프로그램
2 방향 분리기	node_separator
Kway 분리기	Kaffpa를 사용하여 k-partition을 만들고 partition_to_vertex_separator를 만들려면 분리기를 만듭니다.

예제 실행

 ./deploy/node_separator examples/rgg_n_2_15_s0.graph

노드 순서

매트릭스를 희소 그래프로 해석하고 소위 충전물을 최소화하는 노드 순서를 계산하여 큰 희소 행렬에 대해 인수 화와 같은 응용 프로그램이 크게 증가 할 수 있습니다. 중첩 해부 전에 신규 및 기존 데이터 감소 규칙을 철저하게 적용함으로써, 우리는 품질이 향상되고 동시에 다양한 인스턴스에서 달리기 시간이 크게 개선됩니다. Metis가 설치된 경우 빌드 스크립트는 FAST_NODE_ORDERING 프로그램을 컴파일하여 METIS를 실행하기 전에 감소를 실행하여 주문을 계산합니다. 프로그램은 도서관을 통해서도 제공됩니다.

유스 케이스	프로그램
노드 순서	node_ordering (다른 사전 구성)
빠른 노드 순서	FAST_NODE_ORDERING

예제 실행

 ./deploy/node_ordering examples/rgg_n_2_15_s0.graph

 ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graph

가장자리 파티셔닝

Edge 중심 분산 계산은 대규모 프리 네트워크에서 Think-A-Vertex 알고리즘의 단점을 개선하기위한 최근 기술로 나타났습니다. 이 모델의 병렬성을 높이기 위해 Edge Partitioning (가장자리를 대략 똑같이 크기) 블록으로 분할하는 Edge 파티셔닝은 전통적인 (노드 기반) 그래프 파티셔닝의 대안으로 등장했습니다. 우리는 확장 가능한 방식으로 고품질 에지 파티션을 생성하는 빠른 평행하고 순차적 인 분할 및 연결 그래프 구성 알고리즘을 포함합니다. 우리의 기술은 수십억 개의 가장자리가있는 네트워크로, 수천 개의 PES에서 효율적으로 실행됩니다.

유스 케이스	프로그램
가장자리 파티셔닝	Edge_partitioning, distributed_edge_partitioning

예제 실행

 ./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast

 mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial

프로세스 매핑

통신 및 토폴로지 인식 프로세스 매핑은 대규모 분산 메모리 시스템에서 알려진 통신 패턴을 가진 병렬 응용 프로그램에서 통신 시간을 줄이는 강력한 접근법입니다. 우리는 문제를 2 차 할당 문제 (QAP)로 해결하고 프로세서에 프로세스의 초기 매핑을 구성하는 알고리즘과 빠른 로컬 검색 알고리즘을 구성하여 매핑을 더욱 향상시키는 알고리즘을 포함합니다. 드문 커뮤니케이션 패턴 및 계층 적으로 구성된 통신 시스템과 같은 응용 프로그램 및 현대적인 슈퍼 컴퓨터 시스템에 일반적으로 보유한 가정을 활용함으로써 이러한 특수 QAP에 대한보다 강력한 알고리즘에 도달합니다. 우리의 다단계 구조 알고리즘은 완벽하게 균형 잡힌 그래프 파티셔닝 기술을 사용하고 주어진 통신 시스템 계층을 과도하게 활용합니다. v3.0 이후 우리는 지정된 계층 구조를 따라 입력 네트워크를 직접 파티션하여 N-to-1 매핑을 얻은 후 1 대 1 매핑 알고리즘을 호출하여 매핑을 더욱 향상시키는 글로벌 다중 섹션 알고리즘을 포함 시켰습니다.

유스 케이스	프로그램
프로세서 네트워크에 매핑	kaffpa 및 resp와 함께 enable_mapping 옵션을 사용하십시오. 사망자
글로벌 다중 섹션	Global_multisection with resp. 사망자

예제 실행

 ./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100

 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco  --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200

ILP (정확한 솔버) 및 ILP 개선

우리는 주어진 파티션을 개선하기 위해 ILP뿐만 아니라 ILP를 제공합니다. 정수 선형 프로그래밍을 사용하여 여러 로컬 검색에 대한 조합 문제의 이웃을 확장합니다. 이를 통해 우리는 훨씬 더 복잡한 조합을 찾아 솔루션을 더욱 향상시킬 수 있습니다. 그러나 상자에서 문제에 대한 ILP는 일반적으로 큰 입력으로 확장되지 않습니다. 특히 그래프 파티셔닝 문제는 매우 많은 양의 대칭을 가지기 때문에 그래프의 파티션이 주어지면 블록 ID의 각 순열은 동일한 목적과 균형을 갖는 솔루션을 제공합니다. 우리는 모델이라는 훨씬 작은 그래프를 정의하고 정수 선형 프로그램의 최적성에 모델의 그래프 파티셔닝 문제를 해결합니다. 다른 것 외에도이 모델을 사용하면 대칭 브레이킹을 사용할 수있어 훨씬 더 큰 입력으로 확장 할 수 있습니다. 이러한 프로그램을 컴파일하려면 위의 빌드 프로세스에서 cmake에서 cmake를 실행해야합니다 ../ -dcmake_build_type = release -duse_ilp = on 또는 run ./compile_withcmake -duse_ilp = on.

유스 케이스	프로그램
정확한 솔버	ilp_exact
ILP를 통한 개선	ilp_improve

예제 실행

 ./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4

 ./deploy/ilp_exact ./examples/example_weighted.graph  --k 3

Kahip 라이브러리 연결

Kahip은 또한 알고리즘을 코드에 직접 연결하는 라이브러리와 인터페이스를 제공합니다. 매뉴얼의 인터페이스의 세부 사항을 설명합니다. 아래에는 Kahip 라이브러리를 연결하는 예제 프로그램이 나열되어 있습니다. 이 예제는 Misc/example_library_call/에서도 찾을 수 있습니다.

# include < iostream >
# include < sstream >

# include " kaHIP_interface.h "


int main ( int argn, char **argv) {

        std::cout <<  " partitioning graph from the manual "  << std::endl;

        int n            = 5 ;
        int * xadj        = new int [ 6 ];
        xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;

        int * adjncy      = new int [ 12 ];
        adjncy[ 0 ]  = 1 ; adjncy[ 1 ]  = 4 ; adjncy[ 2 ]  = 0 ; adjncy[ 3 ]  = 2 ; adjncy[ 4 ]  = 4 ; adjncy[ 5 ]  = 1 ; 
        adjncy[ 6 ]  = 3 ; adjncy[ 7 ]  = 2 ; adjncy[ 8 ]  = 4 ; adjncy[ 9 ]  = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ; 
        
        double imbalance = 0.03 ;
        int * part        = new int [n];
        int edge_cut     = 0 ;
        int nparts       = 2 ;
        int * vwgt        = NULL ;
        int * adjcwgt     = NULL ;

        kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);

        std::cout <<  " edge cut " <<  edge_cut  << std::endl;
}

파이썬에서 kahip 사용

Kahip은 파이썬에서도 사용할 수 있습니다. Python First Run에서 사용하려면

 python3 -m pip install pybind11

그런 다음 실행하십시오

 ./compile_withcmake.sh BUILDPYTHONMODULE

파이썬 모델을 구축합니다. 이렇게하면 Python 모듈이 만들어지고 Callkahipfrompython.py 예제를 배포 폴더에 넣습니다. 배포 폴더에서 다음을 입력하여이를 실행할 수 있습니다.

 python3 callkahipfrompython.py

예비 지원 만 제공합니다. 즉, compile_withcmake 파일 내부의 Python 경로를 변경해야 할 수도 있습니다. 예는 아래에서도 확인할 수 있습니다.

 import kahip ;

#build adjacency array representation of the graph
xadj           = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy         = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt           = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt        = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance      = 0.03
nblocks        = 2 
seed           = 0

# set mode 
#const int FAST           = 0;
#const int ECO            = 1;
#const int STRONG         = 2;
#const int FASTSOCIAL     = 3;
#const int ECOSOCIAL      = 4;
#const int STRONGSOCIAL   = 5;
mode = 0 

edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt , 
                              adjncy ,  nblocks , imbalance , 
                              supress_output , seed , mode )

print ( edgecut )
print ( blocks )

특허

이 프로그램은 MIT 라이센스에 따라 라이센스가 부여됩니다. 알고리즘을 사용하여 결과를 게시하면 다음 논문을 인용하여 당사의 작업을 인정하십시오.

 @inproceedings{sandersschulz2013,
             AUTHOR = {Sanders, Peter and Schulz, Christian},
             TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
             BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
             SERIES = {LNCS},
             PUBLISHER = {Springer},
             YEAR = {2013},
             VOLUME = {7933},
             PAGES = {164--175}
}

병렬 파티션 자구를 사용하는 경우 다음 논문도 인용하십시오.

 @inproceedings{meyerhenkesandersschulz2017,
             AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
             TITLE = {{Parallel Graph Partitioning for Complex Networks}},
             JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
             VOLUME = {28},
             NUMBER = {9},
             PAGES = {2625--2638},
             YEAR = {2017}
}

매핑 알고리즘을 사용하는 경우 다음 논문도 인용하십시오.

 @inproceedings{schulztraeff2017,
             AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
             TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
             BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
             PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
             VOLUME = {75},
             SERIES = {LIPIcs},
             PAGES = {4:1--4:15},
             YEAR = {2017}
}

Edge Partitioning 알고리즘을 사용하는 경우 다음 논문도 인용하십시오.

 @inproceedings{edgepartitioning2019,
             AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
             TITLE = {{Scalable Edge Partitioning}},
             BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
             PUBLISHER = {SIAM},
             PAGES = {211--225},
             YEAR = {2019}
}

노드 순서 알고리즘을 사용하는 경우 다음 논문도 인용하십시오.

 @article{DBLP:journals/corr/abs-2004-11315,
  author    = {Wolfgang Ost and
               Christian Schulz and
               Darren Strash},
  title     = {Engineering Data Reduction for Nested Dissection},
  journal   = {CoRR},
  volume    = {abs/2004.11315},
  year      = {2020},
  url       = {https://arxiv.org/abs/2004.11315},
  archivePrefix = {arXiv},
  eprint    = {2004.11315},
  timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
  biburl    = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}

파티션을 개선하기 위해 ILP 알고리즘을 사용하는 경우 다음 논문도 인용하십시오.

 @inproceedings{DBLP:conf/wea/HenzingerN018,
  author    = {Alexandra Henzinger and
               Alexander Noe and
               Christian Schulz},
  title     = {ILP-based Local Search for Graph Partitioning},
  booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
  pages     = {4:1--4:15},
  year      = {2018},
  url       = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
  doi       = {10.4230/LIPIcs.SEA.2018.4},
  series    = {LIPIcs},
  volume    = {103},
  publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}