KaHIP скачать - скачать исходный код KaHIP

KaHIP

С/С++

v3.17

Скачать

Кахип v3.17

Рамка разбиения графика Кахип - Карлсруэ. Высококачественное разделение.

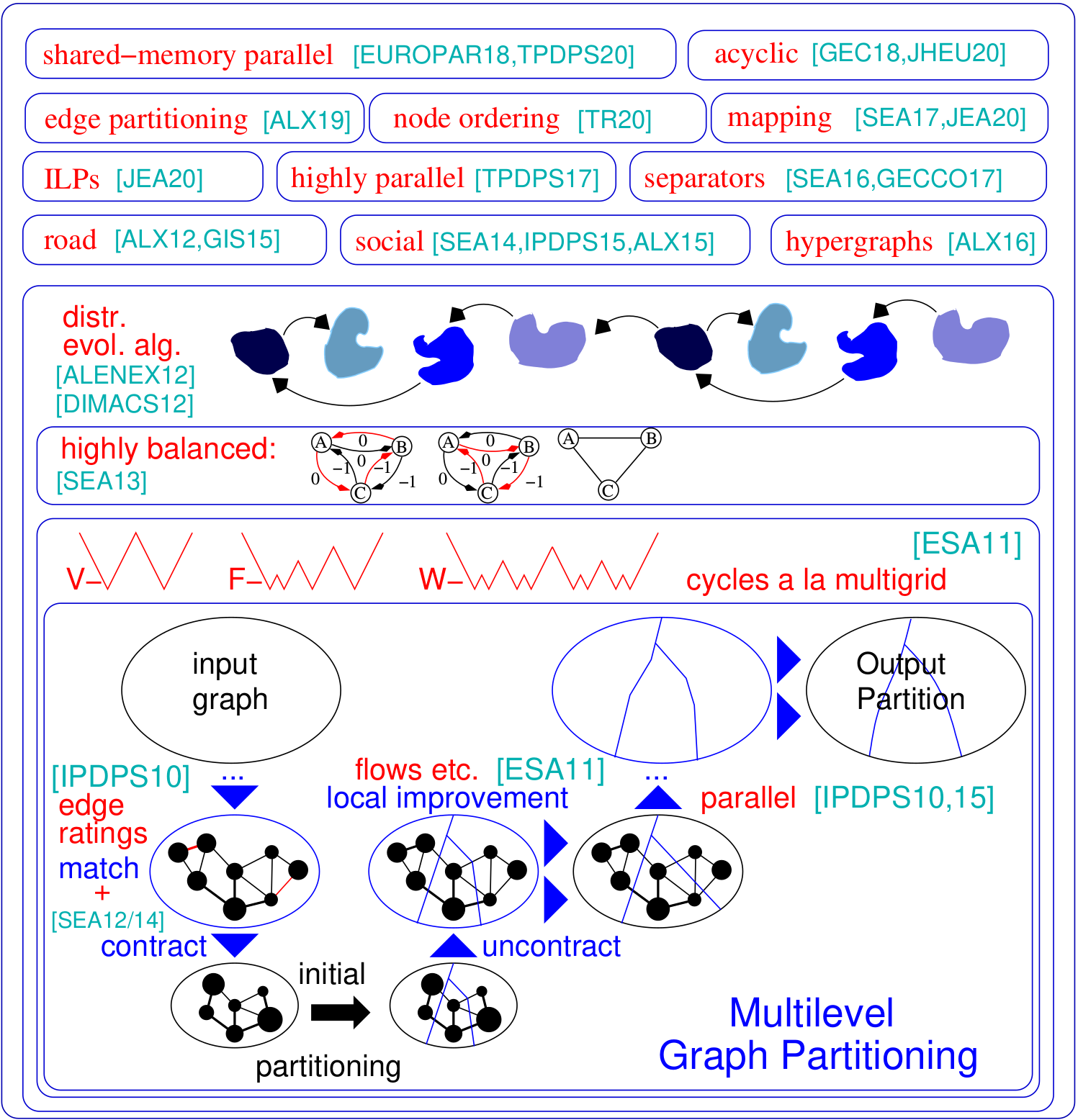
Проблема разбиения графика запрашивает разделение узла графика, установленное на k -блоки, так что количество ребра, которые запускаются между блоками, сводится к минимуму. Kahip - это семья программ распределения графиков. Он включает в себя KAFFPA (Karlsruhe Fast Flow Partitioner), который представляет собой многоуровневый алгоритм разбиения графика, в его вариантах сильные, эко и быстрые, кафпа (Kaffpaevolutionary), который представляет собой параллельный эволюционный алгоритм, который использует комбинированные и мутированные операции, а также Kabapapary, а также EVOLITIOTITIOTITIOTITIOTITIOTITIOTITITIOTITITITITIATIUSTITITITITITIOTITITITIORTY. Более того, специализированные методы включены в разделение дорожных сетей (Buftoon), чтобы вывести сепаратор вершин от данного разделения, а также методы, направленные на эффективное разделение социальных сетей. Вот обзор нашей структуры:

Обзор структуры

Новое в v3.14:

Поддержка Python : Kahip теперь также может использоваться в Python. Смотрите ниже, как это сделать.

Иерархические разделы : Кахип может вычислять иерархические разделы. Все, что вам нужно сделать, это указать иерархию, и Кахип готов к работе и делает многосекцию, как вы указали.

Алгоритмы упорядочения узлов . Здесь мы добавили новые алгоритмы для вычисления заполненных пониженных заказов на графиках.

ILP для еще более высокого качества : ILP обычно не масштабируются до больших случаев. Мы адаптируем их к эвристическому улучшению данного разделения. Мы делаем это, определяя гораздо меньшую модель, которая позволяет нам использовать разрыв симметрии и другие методы, которые делают подход масштабируемым. Мы включаем ILP, которые могут быть использованы в качестве шага после обработки для улучшения высококачественных разделов еще дальше. Коды теперь включены в Кахип.

Tcmalloc: Мы добавили возможность связаться с Tcmalloc. В зависимости от вашей системы это может дать общий более быстрый алгоритм, поскольку он обеспечивает более быстрые операции Malloc.

Быстрее IO : мы добавили опцию в Kaffpa (опция -MMAP_IO), которая значительно ускоряет ввода текстовых файлов -иногда на порядок.

Добавлена поддержка весов вершины и краев в парировании : мы расширили функциональность ввода парирования на чтение взвешенных графиков в формате Metis.

Глобальное картирование многосекции : мы добавили глобальные алгоритмы картирования процессов MultiSection N-1. Это вычисляет лучшее отображение процессов для параллельных приложений, если известна информация о системной иерархии/архитектуре.

Детерминизм в парировании : мы добавили опцию для определения детерминированного запуска париев, т.е. два прогона парика с использованием одного и того же семени всегда будут возвращать один и тот же результат.

Флаг версии : мы добавили опцию для вывода версии, которую вы используете в настоящее время, используйте опцию -версия программ.

Новое в v2.10:

Парирь (параллельное высококачественное разделение): наши методы параллельного разделения распределенной памяти предназначены для разделения иерархически структурированных сетей, таких как веб -графики или социальные сети.

Алгоритмы отображения: наши новые алгоритмы для сопоставления блоков на процессорах, чтобы минимизировать общее время связи на основе иерархических разделов графика задачи и быстрых локальных алгоритмов поиска.

Алгоритмы распределения краев: наши новые алгоритмы для вычисления краевых разделов графиков.

Основной сайт проекта:

https://kahip.github.io

Установка примечания

Загрузка Kahip:

Вы можете скачать Kahip с помощью следующей командной строки:

 git clone https://github.com/KaHIP/KaHIP

Скомпилирование Кахип:

Прежде чем начать, вам нужно установить следующие программные пакеты:

Если вы хотите использовать параллельные алгоритмы, содержащиеся в рамках (например, париль), вам нужен OpenMPI (https://www.open-mpi.org/). Если вы не хотите запустить парижию, вы можете легко избавиться от этой зависимости.

Как только вы установите пакеты, просто введите

 ./compile_withcmake.sh

В этом случае все двоичные файлы, библиотеки и заголовки находятся в папке ./deploy/

Обратите внимание, что этот скрипт обнаруживает количество доступных ядер на вашей машине и использует все их для процесса компиляции. Если вы этого не хотите, установите переменную NCORE на количество ядер, которые вы хотели бы использовать для компиляции.

В качестве альтернативы используйте стандартный процесс сборки Cmake:

 mkdir build
cd build 
cmake ../ -DCMAKE_BUILD_TYPE=Release     
make 
cd ..

В этом случае двоичные файлы, библиотеки и заголовки находятся в папке.

Мы также предоставляем возможность ссылаться на Tcmalloc. Если он установил, запустите CMAKE с дополнительной опцией -duse_tcmalloc = on.

По умолчанию программы упорядочения узлов также составлены. Если у вас установлен METIS, сценарий сборки также компилирует более быструю программу заказа узлов, которая использует сокращения перед вызовом Metis ND. Обратите внимание, что Метис требует gklib (https://github.com/karypislab/gklib).

Если вы используете опцию -duse_ilp = ON и установлен Gurobi, сценарий сборки компилирует программы ILP для улучшения данного разделения ILP_IMPROVE и точного решателя ILP_EXACT . В качестве альтернативы, вы также можете передать эти параметры ./compile_withmake.sh, например:

 ./compile_withcmake -DUSE_ILP=On

Мы также предоставляем возможность поддержать 64 -битные края. Чтобы использовать это, составьте Kahip с опцией -d64bitmode = on.

Наконец, мы предоставляем возможность для детерминизма в парировании, например, два прогона с одним и тем же семенем дадут вам тот же результат. Однако обратите внимание, что этот вариант может снизить качество раздела, поскольку первоначальные алгоритмы разделения не используют сложные мемотические алгоритмы, а только многоуровневые алгоритмы для вычисления начальных разделов. Используйте эту опцию только в том случае, если вы используете Parring в качестве инструмента. Не используйте эту опцию, если вы хотите провести сравнение качества с парированием. Чтобы использовать эту опцию, запустите

 ./compile_withcmake -DDETERMINISTIC_PARHIP=On

Запуск программ

Для описания формата графика (и обширного описания всех других программ), пожалуйста, посмотрите в руководство. Мы приводим здесь короткие примеры.

Обзор программ и использования

Проблема разделения по умолчанию

Эти программы и конфигурации принимают график и разделяют его более или менее последовательно. Здесь мы перечислим Kaffpa и Kaffpae (эволюционная структура) и их конфигурации. В целом, конфигурации таковы, что вы можете потратить много времени в качество решения, используя мемотический алгоритм. Мемотический алгоритм также можно работать параллельно с использованием MPI. В целом, чем больше времени и ресурсов вы инвестируете, тем лучше будет качество вашего разделения. У нас много компромиссов, свяжитесь с нами, если вы не уверены, что лучше всего подходит для вашего приложения. Для описания алгоритма взгляните на ссылки, которые мы перечисляем в руководстве.

Вариант использования	Вход	Программы
График формат		graph_checker
Оценить разделы		оценщик
Быстрое распределение	Сетки	Предварительная конфигурация kaffpa устанавливается быстро
Хорошее распределение	Сетки	предварительная конфигурация kaffpa, установленная на Eco
Очень хорошее распределение	Сетки	предварительная конфигурация kaffpa, установленная на сильную
Высокое качество	Сетки	kaffpae, используйте mpirun, большой срок
Быстрое распределение	Социальная	предварительная конфигурация kaffpa, установленная на fSocial
Хорошее распределение	Социальная	предварительная фигурация Kaffpa, установленная на эзоциальную
Очень хорошее распределение	Социальная	предварительная фигурация Kaffpa, установленная на SSOcial
Высокое качество	Социальная	kaffpae, используйте mpirun, большой срок, предварительная конфигурация Ssocial
Еще более высокое качество		kaffpae, используйте mpirun, большой срок, используйте параметры -mh_enable_tabu_search, -mh_enable_kabape

Пример пробега

 ./deploy/graph_checker ./examples/rgg_n_2_15_s0.graph

 ./deploy/kaffpa ./examples/rgg_n_2_15_s0.graph --k 4  --preconfiguration=strong

 mpirun -n 24 ./deploy/kaffpaE ./examples/rgg_n_2_15_s0.graph --k 4  --time_limit=3600 --mh_enable_tabu_search --mh_enable_kabapE

Распределенная память параллельно разделение

Большая часть проекта представляет собой распределенные параллельные алгоритмы памяти, предназначенные для сетей, имеющих иерархическую структуру кластера, такую как веб -графики или социальные сети. К сожалению, предыдущие предыдущие разместители параллельных графиков, первоначально разработанные для более обычных сетей, похожих на сетки, не очень хорошо работают для сложных сетей. Здесь мы решаем эту проблему, параллелизируя и адаптируя методику распространения метки, первоначально разработанную для кластеризации графиков. Внедряя ограничения размера, распространение метки становится применимым как для увольнения, так и для фазы уточнения многоуровневого разбиения графика. Таким образом, мы используем иерархическую структуру кластера, присутствующую во многих сложных сетях. Мы получаем очень высокое качество, применяя очень параллельный эволюционный алгоритм к самым грубому графику. Полученная система является более масштабируемой и достигает более высокого качества, чем современные системы, такие как Parmetis или PT-Scotch.

Наш параллельный алгоритм распределенной памяти может читать двоичные файлы, а также стандартные файлы формата графиков Metis. Двоичные файлы, как правило, гораздо более масштабируемы, чем чтение текстовых файлов в параллельных приложениях. Способ, чтобы пойти сюда, состоит в том, чтобы сначала преобразовать файл Metis в двоичный файл (заканчивая .bgf), а затем загрузить этот.

Вариант использования	Программы
Параллельное разделение	Parrip, Graph2binary, Graph2binary_external, Toolbox
Распределенная память параллельно, сетка	Парирь с предварительным ножом Ecomesh, Fastmesh, Ultrafastmesh
Распределенная память параллельна, социальная	Париль с предварительнофигсом экосоциальным, быстросоциальным, сверхбыстасоциальным
Преобразовать Метис в двоичный	graph2binary, graph2binary_external
Оценить и преобразовать разделы	набор инструментов

Пример пробега

 ./deploy/graph2binary examples/rgg_n_2_15_s0.graph examples/rgg_n_2_15_s0.bgf

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fastmesh

 mpirun -n 24 ./deploy/parhip ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastmesh

Разделители узлов

Проблема сепаратора узла просит разбить набор узлов графика на три набора A, B и S, так что удаление S отключает A и B. Мы используем основополагающие и локализованные локальные алгоритмы поиска в многоуровневой структуре для вычисления сепараторов узлов. Кахип также может вычислить сепараторы узлов. Он может сделать это со стандартным сепаратором узла (2-й проезд), но также может вычислить разделители узлов K-пути.

Вариант использования	Программы
Двухсторонние сепараторы	node_separator
Квейские сепараторы	Используйте kaffpa для создания K-Partition, затем partition_to_vertex_separator для создания сепаратора

Пример пробега

 ./deploy/node_separator examples/rgg_n_2_15_s0.graph

Узел упорядочения

Такие приложения, как факторизация, могут быть значительно ускорены для больших разреженных матриц, интерпретируя матрицу как редкий график и вычисляя упорядочение узла, которое минимизирует так называемое заполнение. Применяя как новые, так и существующие правила сокращения данных, исчерпывающее перед вложенным диссекцией, мы получаем улучшенное качество и в то же время значительные улучшения времени выполнения в различных случаях. Если Metis установлен, сценарий сборки также компилирует программу FAST_NODE_ORDERING, которая запускает сокращение перед запуском METIS для вычисления заказа. Программы также доступны через библиотеку.

Вариант использования	Программы
Узел упорядочения	node_ordering (с разными предварительными фигурациями)
Быстрый узел	fast_node_ordering

Пример пробега

 ./deploy/node_ordering examples/rgg_n_2_15_s0.graph

 ./deploy/fast_node_ordering examples/rgg_n_2_15_s0.graph

Краевая перегородка

Распределенные вычисления, ориентированные на краю, появились в качестве недавней методики для улучшения недостатков алгоритмов Think-A-A-Vertex в крупномасштабных сетях. Чтобы увеличить параллелизм по этой модели, края разбиения-ребра разделения на примерно одинаковые блоки-стало альтернативой традиционным (на основе узлов) раздела графика. Мы включаем быстрый параллельный и последовательный алгоритм построения графика разделения и подключения, который дает высококачественные краевые разделы масштабируемым образом. Наша техника масштабируется сети с миллиардами краев и эффективно работает на тысячах Пес.

Вариант использования	Программы
Краевая перегородка	Edge_Partitioning, Diviubted_edge_partitioning

Пример пробега

 ./deploy/edge_partitioning ./examples/rgg_n_2_15_s0.graph --k 4 --preconfiguration=fast

 mpirun -n 4 ./deploy/distributed_edge_partitioning ./examples/rgg_n_2_15_s0.bgf --k 4 --preconfiguration=fastsocial

Картирование процесса

Картирование процесса общения и топологии является мощным подходом для сокращения времени связи в параллельных приложениях с известными моделями связи в крупных распределенных системах памяти. Мы рассматриваем проблему как к квадратичному назначению (QAP) и включаем алгоритмы для построения начальных отображений процессов для процессоров, а также быстрых локальных алгоритмов поиска для дальнейшего улучшения отображений. Используя предположения, которые обычно придерживаются приложений и современных суперкомпьютерных систем, таких как редкие модели связи и иерархически организованные системы связи, мы получаем значительно более мощные алгоритмы для этих специальных QAP. Наши многоуровневые конструктивные алгоритмы используют идеально сбалансированные методы распределения графиков и чрезмерно использовать данную иерархию системы связи. Поскольку v3.0 мы включили глобальные многосекционные алгоритмы, которые непосредственно разделяют входную сеть вдоль указанной иерархии, чтобы получить отображение от N-1, а затем вызовут алгоритмы сопоставления 1-1, чтобы еще больше улучшить картирование.

Вариант использования	Программы
Картирование с сети обработчиков	kaffpa и используйте опцию enable_mapping с соответствующим. Perconfigurations
Глобальный многосекция	Global_multisection с соответствующим. Perconfigurations

Пример пробега

 ./deploy/kaffpa examples/rgg_n_2_15_s0.graph --k 256 --preconfiguration=eco --enable_mapping --hierarchy_parameter_string=4:8:8 --distance_parameter_string=1:10:100

 ./deploy/global_multisection examples/rgg_n_2_15_s0.graph --preconfiguration=eco  --hierarchy_parameter_string=4:3:3:3 --distance_parameter_string=1:10:100:200

Улучшения ILP (точный решатель) и ILP

Мы предоставляем ILP, а также ILP для улучшения данного разделения. Мы расширяем район проблемы комбинирования для нескольких локальных поисков, используя целочисленное линейное программирование. Это позволяет нам найти еще более сложные комбинации и, следовательно, для дальнейшего улучшения решений. Тем не менее, из коробки те, которые ILP для проблемы обычно не масштабируются до больших входов, в частности потому, что проблема разбиения графика имеет очень большое количество симметрии - учитывая раздел графика, каждая перестановка идентификаторов блока дает решение, имеющее одинаковую цель и баланс. Мы определяем гораздо меньший график, называемый моделью, и решаем задачу разделения графика на модели к оптимальности с помощью целочисленной линейной программы. Помимо других вещей, эта модель позволяет нам использовать нарушение симметрии, что позволяет нам масштабировать до гораздо больших входов. Чтобы скомпилировать эти программы, вам необходимо запустить CMAKE в процессе сборки выше как CMAKE ../ -DCMAKE_BUILD_TYPE = релиз -DUSE_ILP = ON или RUN ./COMPILE_WITHCMAKE -DUSE_ILP = ON.

Вариант использования	Программы
Точный решатель	ilp_exact
Улучшение через ILP	ilp_improve

Пример пробега

 ./deploy/ilp_improve ./examples/rgg_n_2_15_s0.graph --k 4 --input_partition=tmppartition4

 ./deploy/ilp_exact ./examples/example_weighted.graph  --k 3

Связывание библиотеки Кахип

Kahip также предлагает библиотеки и интерфейсы, чтобы связать алгоритмы непосредственно с вашим кодом. Мы объясняем детали интерфейса в руководстве. Ниже мы перечисляем примерную программу, которая связывает библиотеку Кахип. Этот пример также можно найти в MISC/example_library_call/.

# include < iostream >
# include < sstream >

# include " kaHIP_interface.h "


int main ( int argn, char **argv) {

        std::cout <<  " partitioning graph from the manual "  << std::endl;

        int n            = 5 ;
        int * xadj        = new int [ 6 ];
        xadj[ 0 ] = 0 ; xadj[ 1 ] = 2 ; xadj[ 2 ] = 5 ; xadj[ 3 ] = 7 ; xadj[ 4 ] = 9 ; xadj[ 5 ] = 12 ;

        int * adjncy      = new int [ 12 ];
        adjncy[ 0 ]  = 1 ; adjncy[ 1 ]  = 4 ; adjncy[ 2 ]  = 0 ; adjncy[ 3 ]  = 2 ; adjncy[ 4 ]  = 4 ; adjncy[ 5 ]  = 1 ; 
        adjncy[ 6 ]  = 3 ; adjncy[ 7 ]  = 2 ; adjncy[ 8 ]  = 4 ; adjncy[ 9 ]  = 0 ; adjncy[ 10 ] = 1 ; adjncy[ 11 ] = 3 ; 
        
        double imbalance = 0.03 ;
        int * part        = new int [n];
        int edge_cut     = 0 ;
        int nparts       = 2 ;
        int * vwgt        = NULL ;
        int * adjcwgt     = NULL ;

        kaffpa (&n, vwgt, xadj, adjcwgt, adjncy, &nparts, &imbalance, false , 0 , ECO, & edge_cut, part);

        std::cout <<  " edge cut " <<  edge_cut  << std::endl;
}

Использование Kahip в Python

Кахип также можно использовать в Python. Если вы хотите использовать его в Python First Run

 python3 -m pip install pybind11

Затем беги

 ./compile_withcmake.sh BUILDPYTHONMODULE

Чтобы построить модель Python. Это построит модуль Python, а также поместит пример Callkahipfrompython.py в папку развертывания. Вы можете запустить это, набрав следующее в папке Deploy:

 python3 callkahipfrompython.py

Обратите внимание, что мы предоставляем только предварительную поддержку, то есть вам может потребоваться изменить некоторые пути на Python внутри файла compile_withcmake. Пример также можно найти ниже:

 import kahip ;

#build adjacency array representation of the graph
xadj           = [ 0 , 2 , 5 , 7 , 9 , 12 ];
adjncy         = [ 1 , 4 , 0 , 2 , 4 , 1 , 3 , 2 , 4 , 0 , 1 , 3 ];
vwgt           = [ 1 , 1 , 1 , 1 , 1 ]
adjcwgt        = [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ]
supress_output = 0
imbalance      = 0.03
nblocks        = 2 
seed           = 0

# set mode 
#const int FAST           = 0;
#const int ECO            = 1;
#const int STRONG         = 2;
#const int FASTSOCIAL     = 3;
#const int ECOSOCIAL      = 4;
#const int STRONGSOCIAL   = 5;
mode = 0 

edgecut , blocks = kahip . kaffpa ( vwgt , xadj , adjcwgt , 
                              adjncy ,  nblocks , imbalance , 
                              supress_output , seed , mode )

print ( edgecut )
print ( blocks )

Лицензия

Программа лицензирована по лицензии MIT. Если вы публикуете результаты, используя наши алгоритмы, пожалуйста, подтвердите нашу работу, цитируя следующую статью:

 @inproceedings{sandersschulz2013,
             AUTHOR = {Sanders, Peter and Schulz, Christian},
             TITLE = {{Think Locally, Act Globally: Highly Balanced Graph Partitioning}},
             BOOKTITLE = {Proceedings of the 12th International Symposium on Experimental Algorithms (SEA'13)},
             SERIES = {LNCS},
             PUBLISHER = {Springer},
             YEAR = {2013},
             VOLUME = {7933},
             PAGES = {164--175}
}

Если вы используете наш параллельный переборщик, также укажите следующую статью:

 @inproceedings{meyerhenkesandersschulz2017,
             AUTHOR = {Meyerhenke, Henning and Sanders, Peter and Schulz, Christian},
             TITLE = {{Parallel Graph Partitioning for Complex Networks}},
             JOURNAL = {IEEE Transactions on Parallel and Distributed Systems (TPDS)},
             VOLUME = {28},
             NUMBER = {9},
             PAGES = {2625--2638},
             YEAR = {2017}
}

Если вы используете алгоритм отображения, также укажите следующую статью:

 @inproceedings{schulztraeff2017,
             AUTHOR = {Schulz, Christian and Träff, Jesper Larsson},
             TITLE = {{Better Process Mapping and Sparse Quadratic Assignment}},
             BOOKTITLE = {Proceedings of the 16th International Symposium on Experimental Algorithms (SEA'17)},
             PUBLISHER = {Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik},
             VOLUME = {75},
             SERIES = {LIPIcs},
             PAGES = {4:1--4:15},
             YEAR = {2017}
}

Если вы используете алгоритмы разделения края, также укажите следующую статью:

 @inproceedings{edgepartitioning2019,
             AUTHOR = {Schlag, Sebastian and Schulz, Christian and Seemaier, Daniel and Strash, Darren},
             TITLE = {{Scalable Edge Partitioning}},
             BOOKTITLE = {Proceedings of the 21th Workshop on Algorithm Engineering and Experimentation (ALENEX)},
             PUBLISHER = {SIAM},
             PAGES = {211--225},
             YEAR = {2019}
}

Если вы используете алгоритмы заказа узлов, также укажите следующую статью:

 @article{DBLP:journals/corr/abs-2004-11315,
  author    = {Wolfgang Ost and
               Christian Schulz and
               Darren Strash},
  title     = {Engineering Data Reduction for Nested Dissection},
  journal   = {CoRR},
  volume    = {abs/2004.11315},
  year      = {2020},
  url       = {https://arxiv.org/abs/2004.11315},
  archivePrefix = {arXiv},
  eprint    = {2004.11315},
  timestamp = {Tue, 28 Apr 2020 16:10:02 +0200},
  biburl    = {https://dblp.org/rec/journals/corr/abs-2004-11315.bib},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}

Если вы используете алгоритмы ILP, чтобы улучшить раздел, также укажите следующую статью:

 @inproceedings{DBLP:conf/wea/HenzingerN018,
  author    = {Alexandra Henzinger and
               Alexander Noe and
               Christian Schulz},
  title     = {ILP-based Local Search for Graph Partitioning},
  booktitle = {17th International Symposium on Experimental Algorithms, {SEA} 2018},
  pages     = {4:1--4:15},
  year      = {2018},
  url       = {https://doi.org/10.4230/LIPIcs.SEA.2018.4},
  doi       = {10.4230/LIPIcs.SEA.2018.4},
  series    = {LIPIcs},
  volume    = {103},
  publisher = {Schloss Dagstuhl - Leibniz-Zentrum f{"{u}}r Informatik}
}