模拟退火方法的最简单实现(来自DPEA)
pip install SimplestSimulatedAnnealing
这是用于最小化功能的进化算法。
步骤:
f必须最小化x0 (可以是随机的)mut 。此功能应使用有关x0和温度T信息给出新的(可以是随机) x1解决方案。cooling制度(温度行为)Tx0解决方案和f(x0)最佳分数x1 = mut(x0)并计算f(x1)f(x1) < f(x0) ,我们找到了更好的解决方案x0 = x1 。否则,我们可以用x0替换x1 ,概率等于exp((f(x0) - f(x1)) / T)cooling功能降低T : T = cooling(T)导入软件包:
import math
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling , simple_continual_mutation确定最小功能(rastrigin):
def Rastrigin ( arr ):
return 10 * arr . size + np . sum ( arr ** 2 ) - 10 * np . sum ( np . cos ( 2 * math . pi * arr ))
dim = 5我们将使用最简单的高斯突变:
mut = simple_continual_mutation ( std = 0.5 )创建模型对象(设置功能和维度):
model = SimulatedAnnealing ( Rastrigin , dim )开始搜索并查看报告:
best_solution , best_val = model . run (
start_solution = np . random . uniform ( - 5 , 5 , dim ),
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80
)
model . plot_report ( save_as = 'simple_example.png' )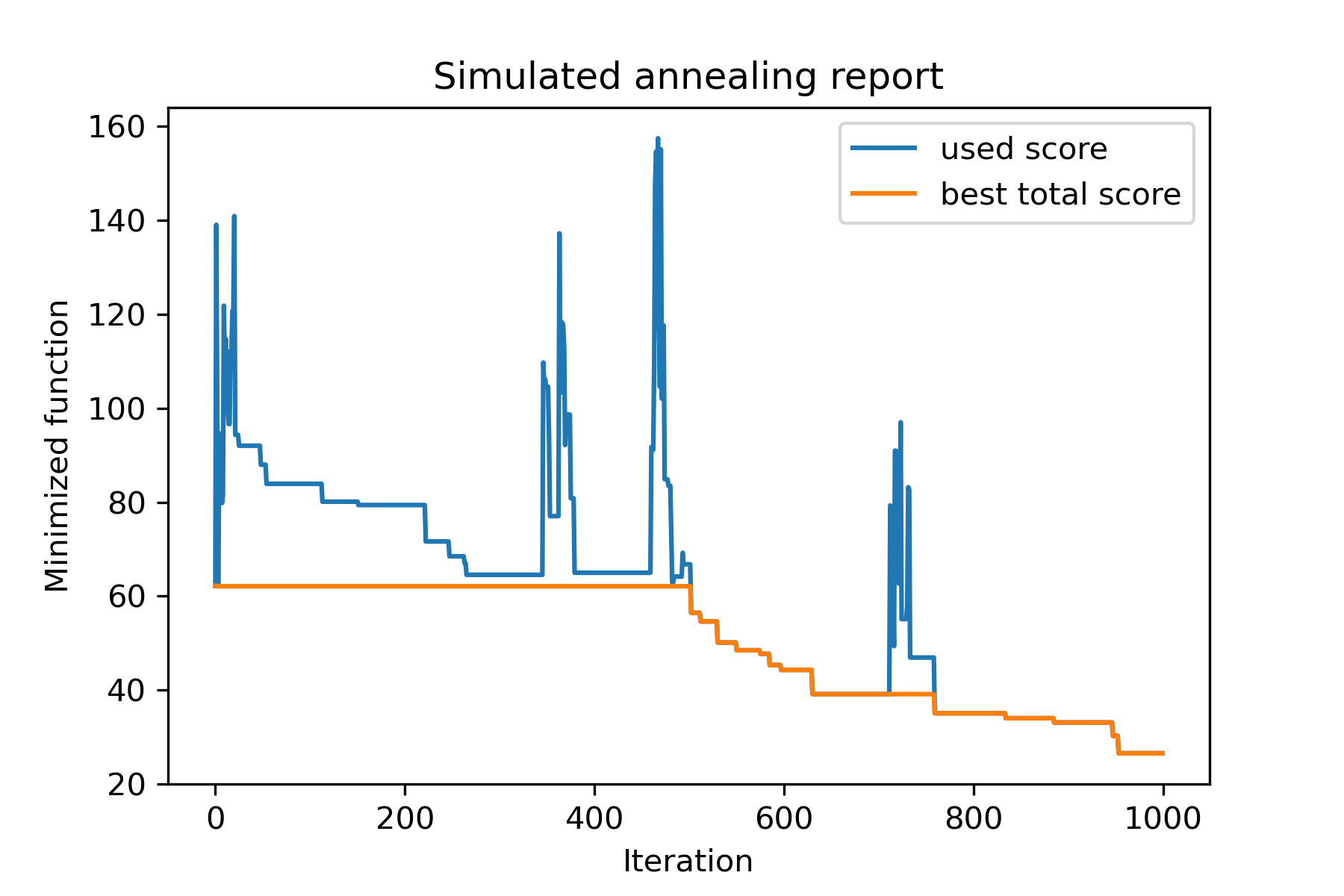
包装的主要方法是run() 。让我们检查一下它的论点:
model . run ( start_solution ,
mutation ,
cooling ,
start_temperature ,
max_function_evals = 1000 ,
max_iterations_without_progress = 250 ,
step_for_reinit_temperature = 90 ,
reinit_from_best = False ,
seed = None )在哪里:
start_solution :numpy array;应该从中启动的解决方案。
mutation :功能(数组,数组/编号)。功能如
def mut ( x_as_array , temperature_as_array_or_one_number ):
# some code
return new_x_as_array此功能将从现有的新解决方案创建新的解决方案。参见
cooling :冷却功能 /功能列表。冷却功能或列表。看
start_temperature :数字或数字数组(list/tuple)。开始温度。可以是一个数字或数字数字。
max_function_evals :int,可选。功能评估的最大数量。默认值为1000。
max_iterations_without_progress :int,可选。没有全球进步的最大迭代次数。默认值为250。
step_for_reinit_temperature :int,可选。在没有进度的迭代次数之后,将像开始一样初始化温度。默认值为90。
reinit_from_best :布尔值,可选。从最佳溶液(或从最后一个当前溶液)开始,从最佳溶液开始算法。默认值为false。
seed :int/无,可选。随机种子(如果需要)
算法的重要部分是冷却功能。该功能控制温度值取决于当前迭代的数量,当前温度和起始温度。您可以使用模式创建自己的冷却功能:
def func ( T_last , T0 , k ):
# some code
return T_new这里T_last (int/float)是先前迭代的温度值, T0 (int/float)是起始温度, k (int> 0)是迭代的数量。您应该使用其中一些信息来创建新的温度T_new 。
强烈建议建立您的功能以创建正温度。
在Cooling类中,有几个冷却功能:
Cooling.linear(mu, Tmin = 0.01)Cooling.exponential(alpha = 0.9)Cooling.reverse(beta = 0.0005)Cooling.logarithmic(c, d = 1) - 不建议Cooling.linear_reverse()您可以使用SimulatedAnnealing.plot_temperature方法看到冷却函数的行为。让我们看看几个例子:
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
# simplest way to set cooling regime
temperature = 100
cooling = Cooling . reverse ( beta = 0.001 )
# we can temperature behaviour using this code
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse.png' )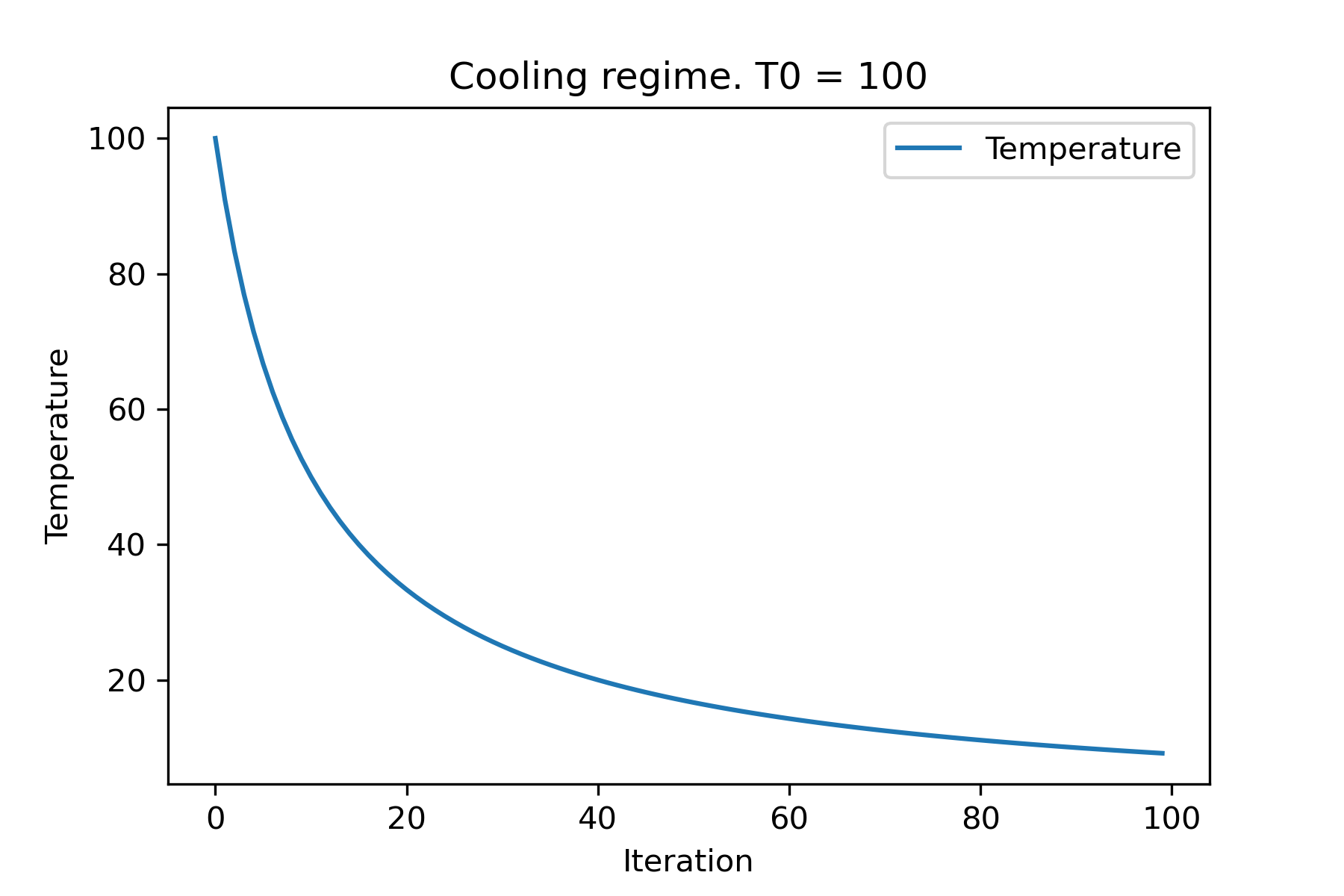
# we can set several temparatures (for each dimention)
temperature = [ 150 , 100 , 50 ]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse_diff_temp.png' )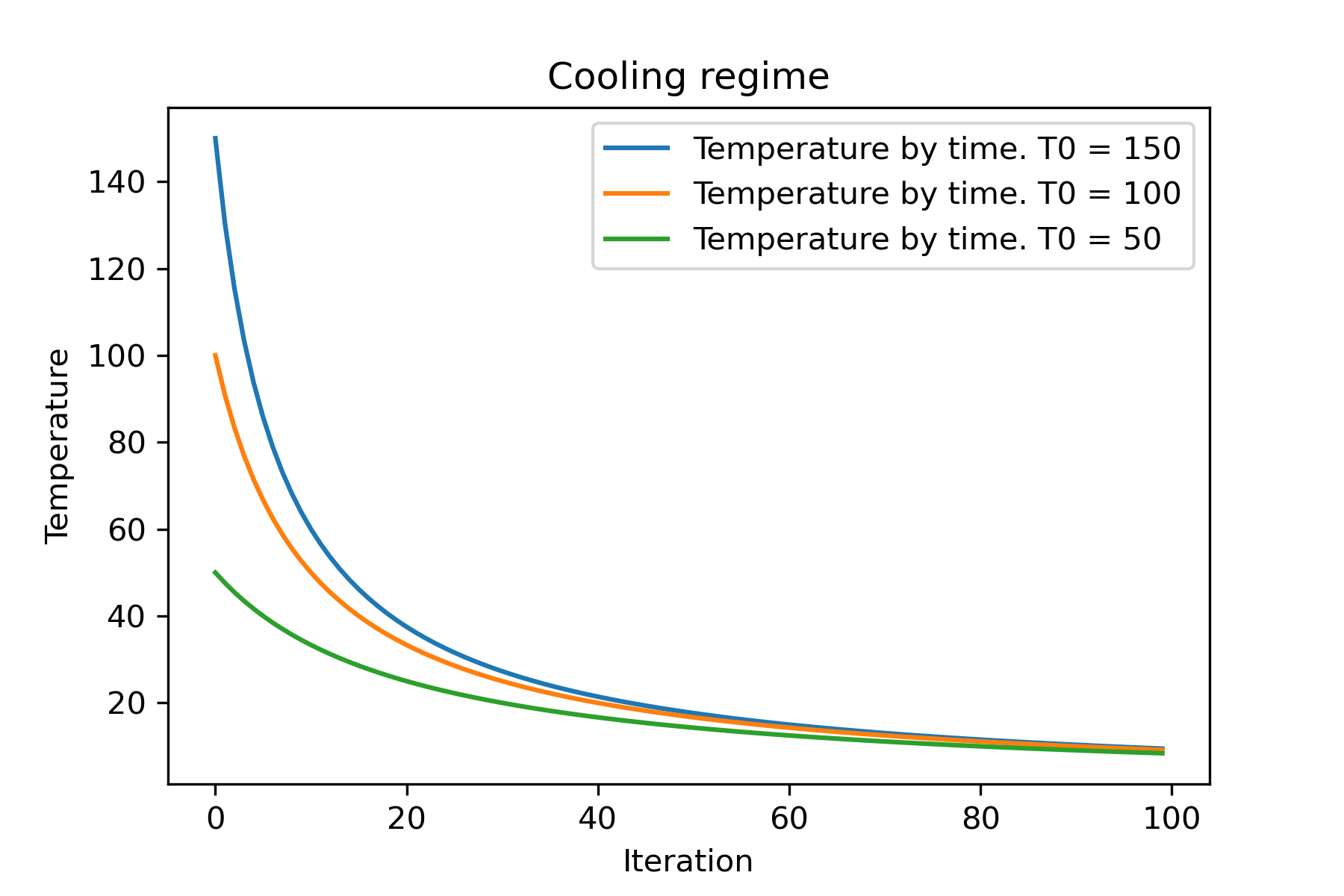
# or several coolings (for each dimention)
temperature = 100
cooling = [
Cooling . reverse ( beta = 0.0001 ),
Cooling . reverse ( beta = 0.0005 ),
Cooling . reverse ( beta = 0.001 )
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse_diff_beta.png' )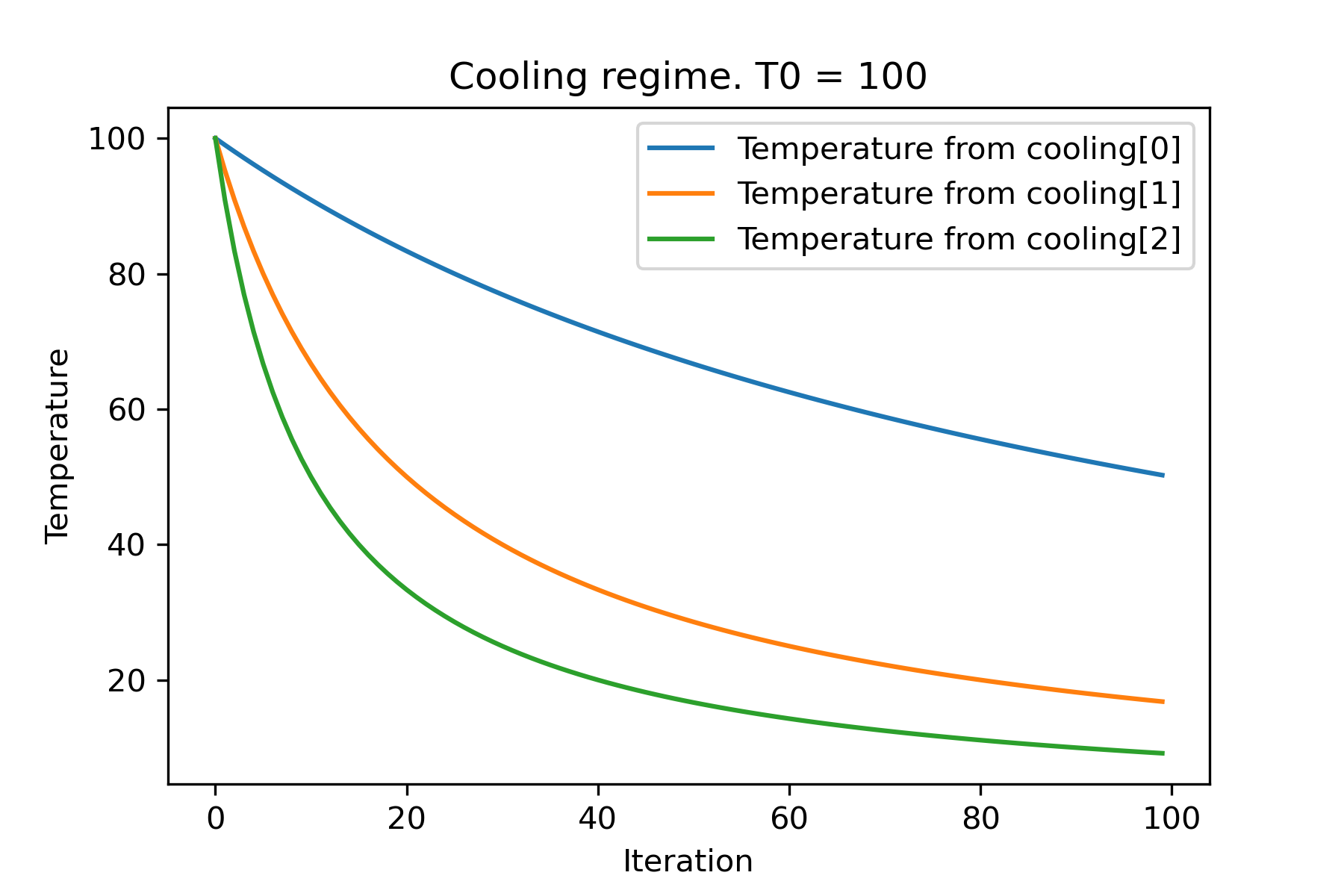
# all supported coolling regimes
temperature = 100
cooling = [
Cooling . linear ( mu = 1 ),
Cooling . reverse ( beta = 0.0007 ),
Cooling . exponential ( alpha = 0.85 ),
Cooling . linear_reverse (),
Cooling . logarithmic ( c = 100 , d = 1 )
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'diff_temp.png' )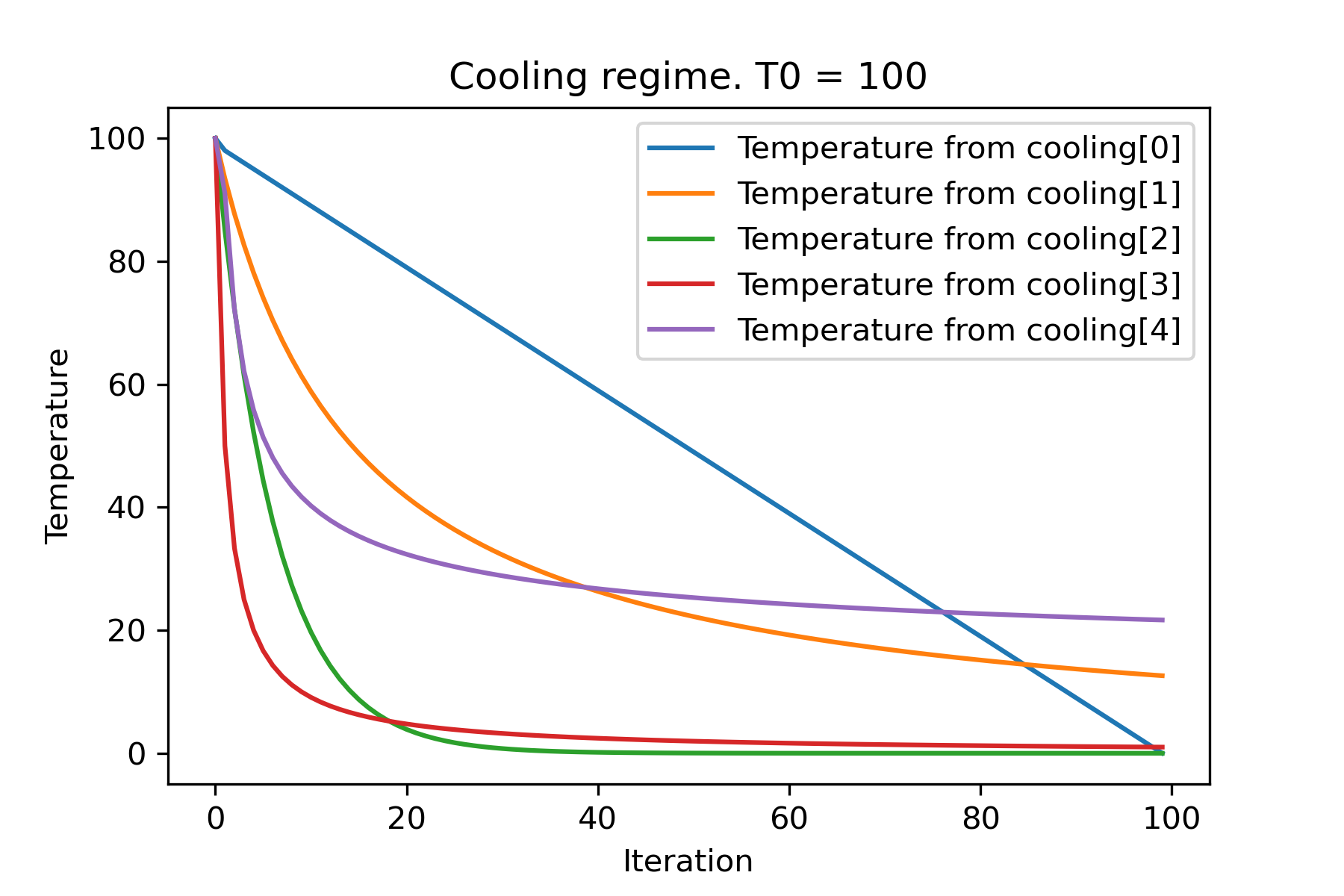
# and we can set own temperature and cooling for each dimention!
temperature = [ 100 , 125 , 150 ]
cooling = [
Cooling . exponential ( alpha = 0.85 ),
Cooling . exponential ( alpha = 0.9 ),
Cooling . exponential ( alpha = 0.95 ),
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'diff_temp_and_cool.png' )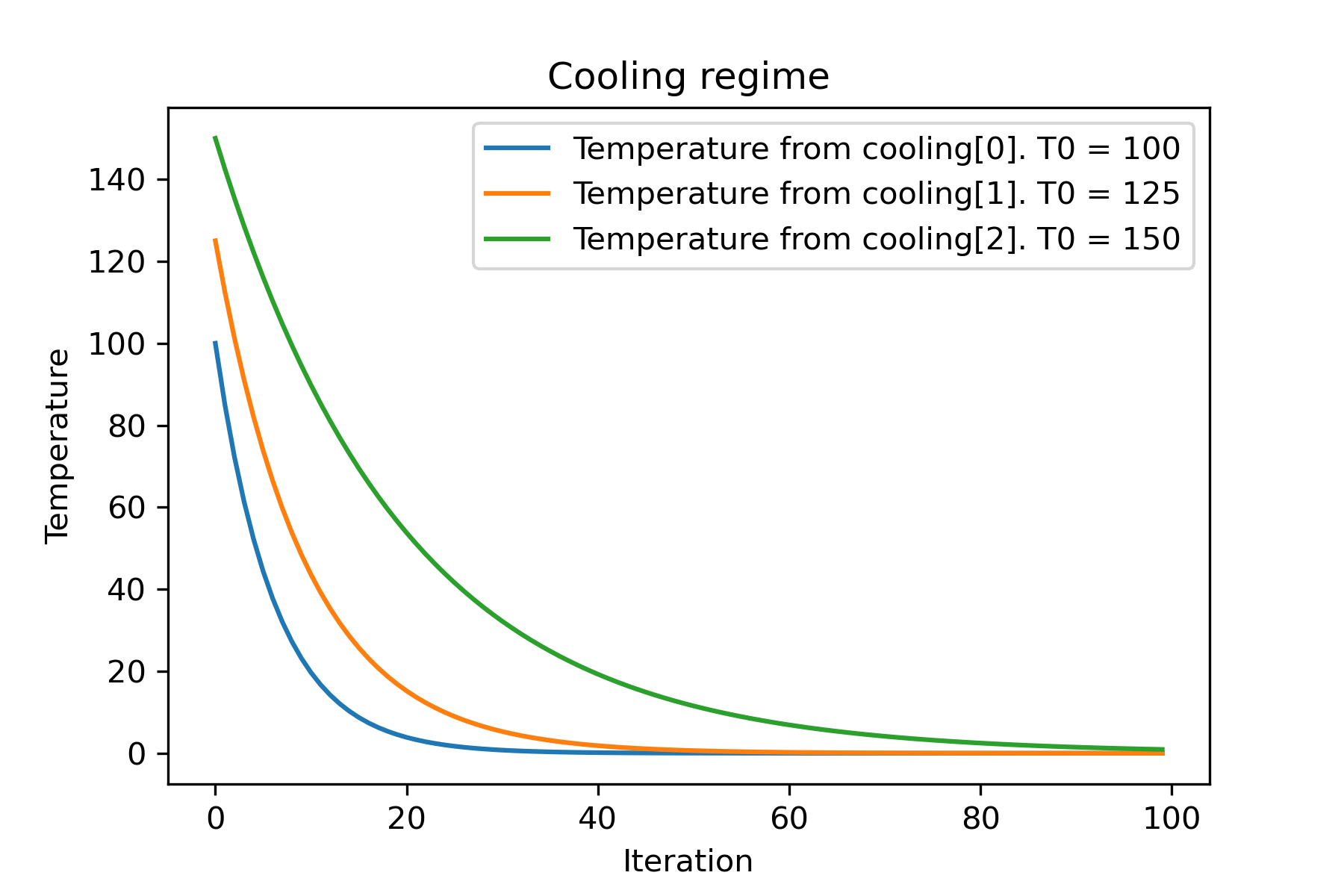
为什么有这么多的冷却机制?对于某些任务,其中一个可能会更好!在此脚本中,我们可以测试不同的冷却功能:
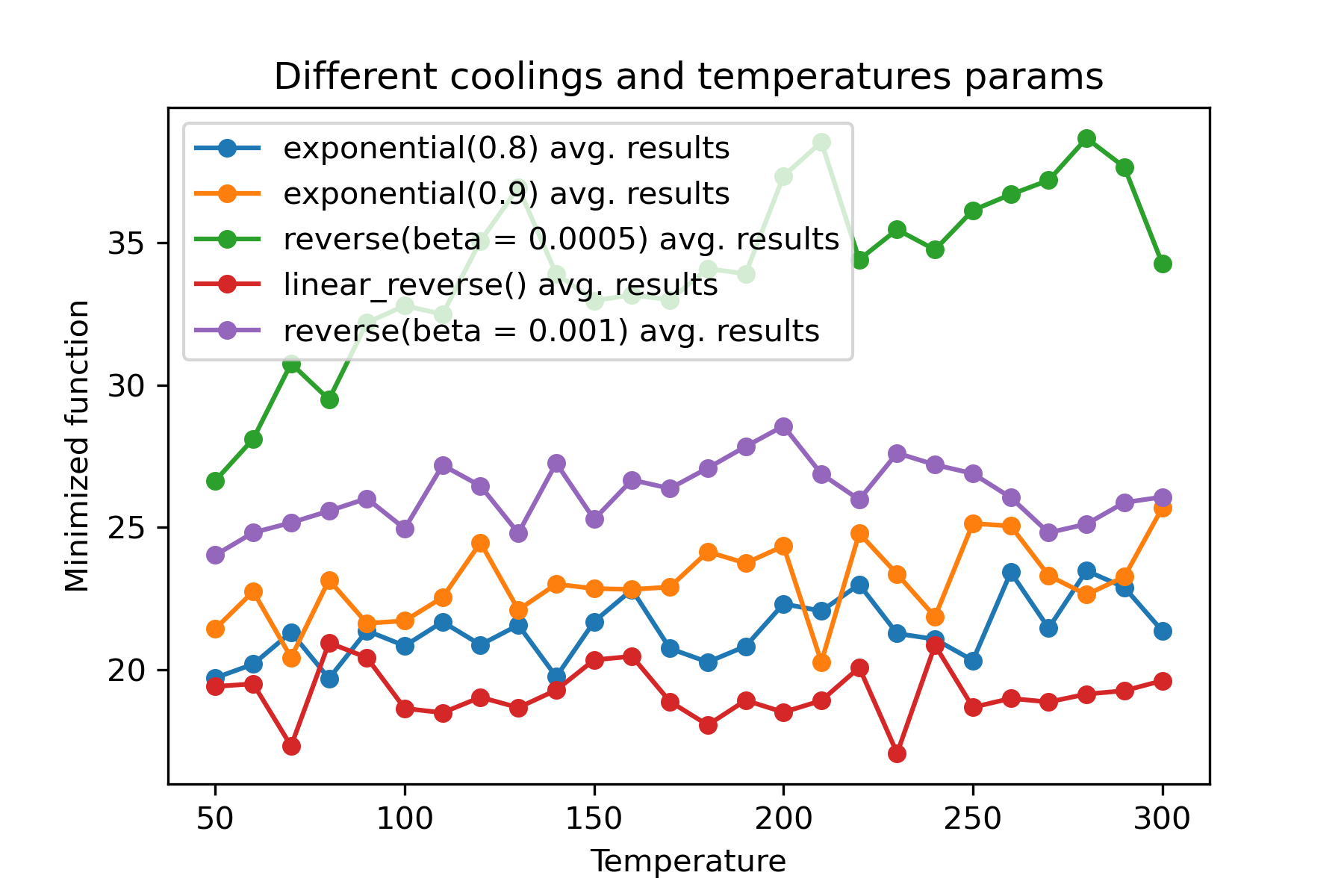
使用不同的冷却并为每个维度开始温度是惊人的功能:
import math
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling , simple_continual_mutation
def Rastrigin ( arr ):
return 10 * arr . size + np . sum ( arr ** 2 ) - 10 * np . sum ( np . cos ( 2 * math . pi * arr ))
dim = 5
model = SimulatedAnnealing ( Rastrigin , dim )
best_solution , best_val = model . run (
start_solution = np . random . uniform ( - 5 , 5 , dim ),
mutation = simple_continual_mutation ( std = 1 ),
cooling = [ # different cooling for each dimention
Cooling . exponential ( 0.8 ),
Cooling . exponential ( 0.9 ),
Cooling . reverse ( beta = 0.0005 ),
Cooling . linear_reverse (),
Cooling . reverse ( beta = 0.001 )
],
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 250 ,
step_for_reinit_temperature = 90 ,
reinit_from_best = False
)
print ( best_val )
model . plot_report ( save_as = 'different_coolings.png' )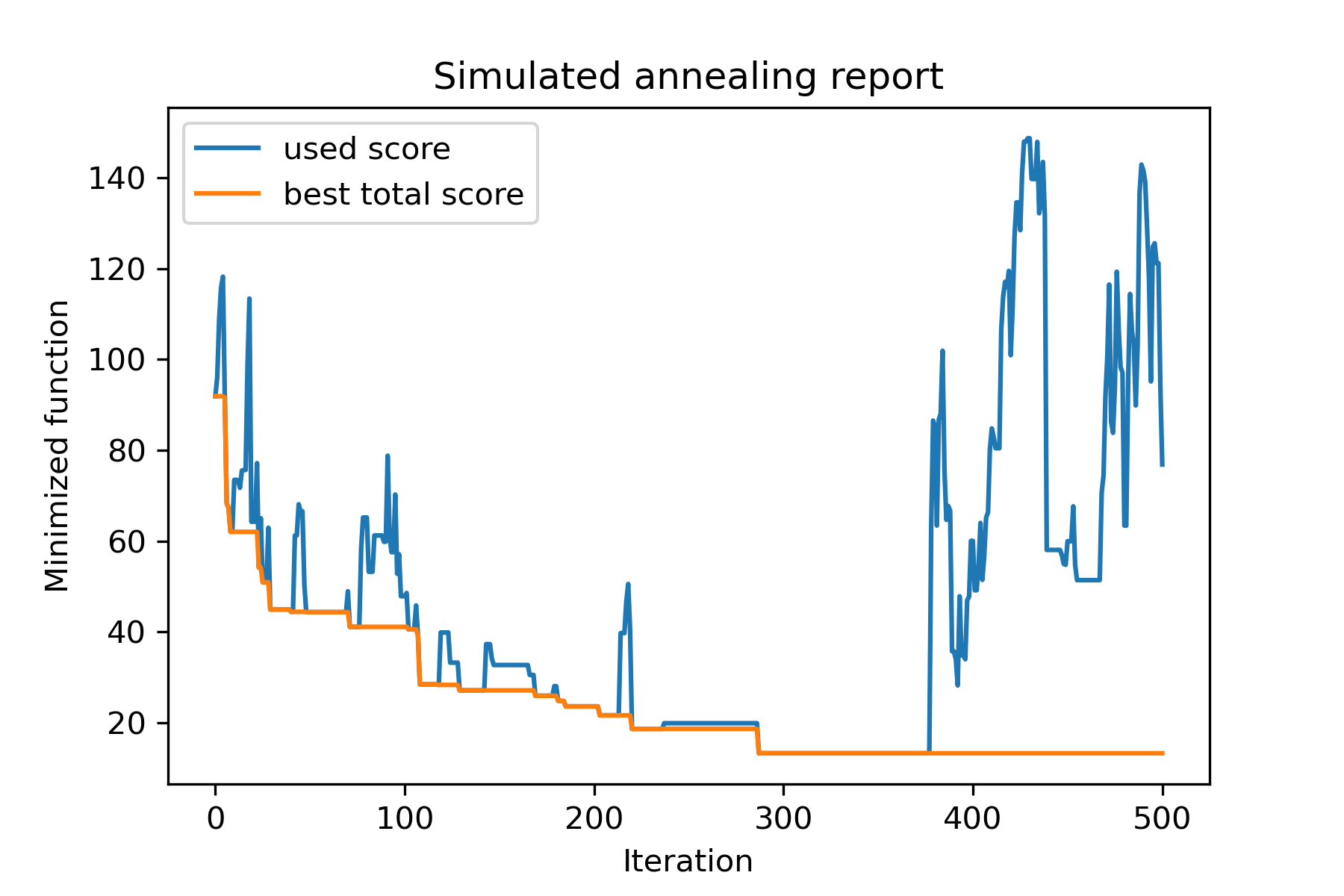
使用多种冷却的主要原因是每个维度的指定行为。例如,空间的一个维度可能比第二维度宽得多,因此最好使用更广泛的搜索对第一维。 U可以使用特殊的mut功能,使用不同的start temperatures和不同的coolings来生产它。
使用多种冷却的另一个原因是选择方法:对于每个维度,适用于好的解决方案和坏解决方案之间的多个冷却。因此,它增加了找到更好的解决方案的机会。
突变函数是最重要的参数。它使用有关当前对象和温度的信息确定创建新对象的行为。我建议在创建mut函数时计算这些原则:
让我们回想一下mut的结构:
def mut ( x_as_array , temperature_as_array_or_one_number ):
# some code
return new_x_as_array这里x_as_array是当前的解决方案, new_x_as_array是突变的解决方案(随机且与您记住相同)。您还要记住, temperature_as_array_or_one_number仅用于非媒体清理解决方案。否则(使用几种冷却或两者两者的几个起始温度时)是numpy阵列。见示例
在此示例中,我显示了如何使用n对象从设置中选择k对象,以最大程度地减少某些函数(在此示例中:中位数的绝对值):
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
SEED = 3
np . random . seed ( SEED )
Set = np . random . uniform ( low = - 15 , high = 5 , size = 100 ) # all set
dim = 10 # how many objects should we choose
indexes = np . arange ( Set . size )
# minimized function -- subset with best |median|
def min_func ( arr ):
return abs ( np . median ( Set [ indexes [ arr . astype ( bool )]]))
# zero vectors with 'dim' ones at random positions
start_solution = np . zeros ( Set . size )
start_solution [ np . random . choice ( indexes , dim , replace = False )] = 1
# mutation function
# temperature is the number cuz we will use only 1 cooling, but it's not necessary to use it)
def mut ( x_as_array , temperature_as_array_or_one_number ):
mask_one = x_as_array == 1
mask_zero = np . logical_not ( mask_one )
new_x_as_array = x_as_array . copy ()
# replace some zeros with ones
new_x_as_array [ np . random . choice ( indexes [ mask_one ], 1 , replace = False )] = 0
new_x_as_array [ np . random . choice ( indexes [ mask_zero ], 1 , replace = False )] = 1
return new_x_as_array
# creating a model
model = SimulatedAnnealing ( min_func , dim )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80 ,
seed = SEED
)
model . plot_report ( save_as = 'best_subset.png' )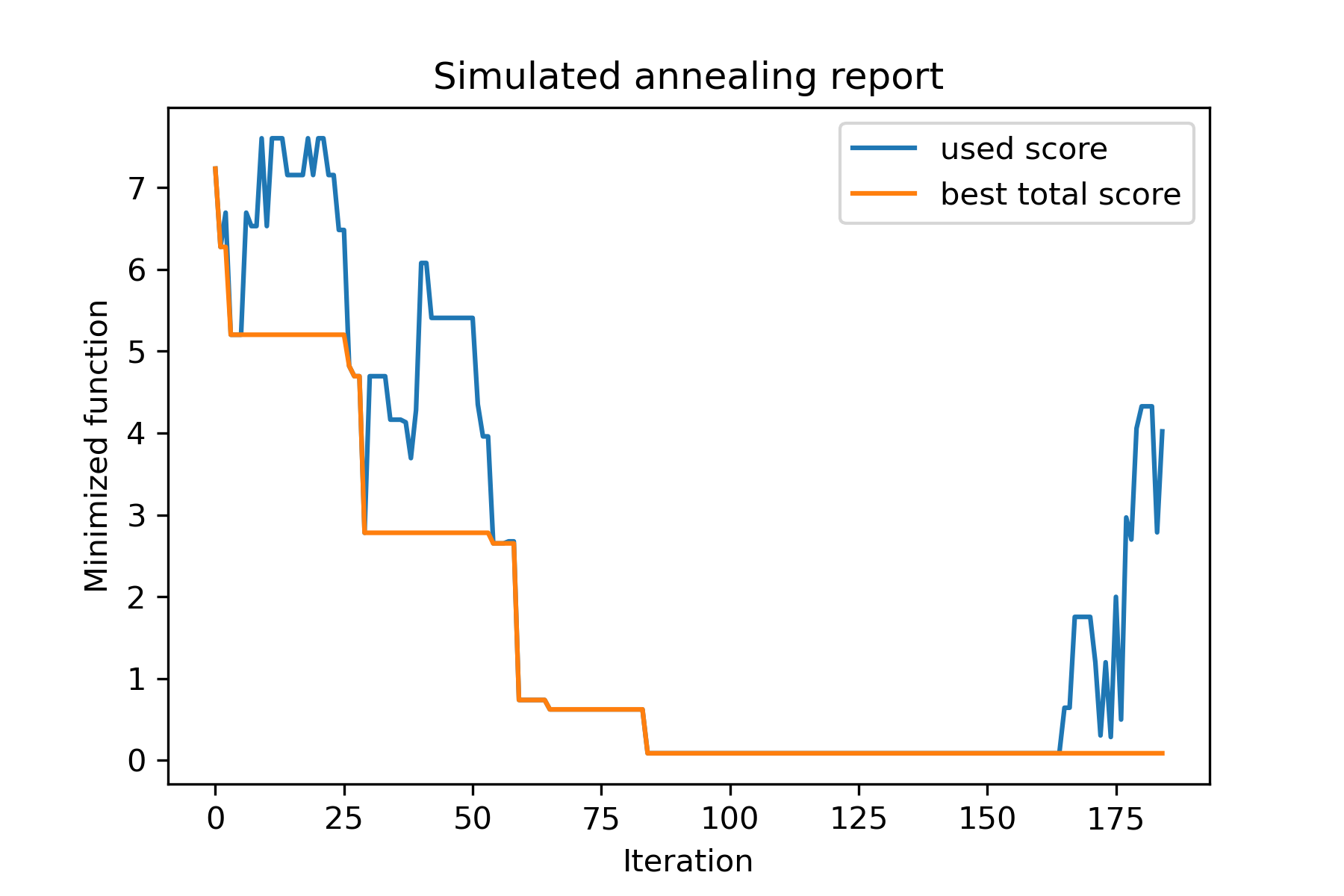
让我们看一下这项任务:
split set of values {v1, v2, v3, ..., vn} to sets 0, 1, 2, 3
with their sizes (volumes determined by user) to complete best sets metric
解决它的方法之一:
from collections import defaultdict
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
################### useful methods
def counts_to_vec ( dic_count ):
"""
converts dictionary like {1: 3, 2: 4}
to array [1, 1, 1, 2, 2, 2, 2]
"""
arrs = [ np . full ( val , fill_value = key ) for key , val in dic_count . items ()]
return np . concatenate ( tuple ( arrs ))
def vec_to_indexes_dict ( vector ):
"""
converts vector like [1, 0, 1, 2, 2]
to dictionary with indexes {1: [0, 2], 2: [3, 4]}
"""
res = defaultdict ( list )
for i , v in enumerate ( vector ):
res [ v ]. append ( i )
return { int ( key ): np . array ( val ) for key , val in res . items () if key != 0 }
#################### START PARAMS
SEED = 3
np . random . seed ( SEED )
Set = np . random . uniform ( low = - 15 , high = 5 , size = 100 ) # all set
Set_indexes = np . arange ( Set . size )
# how many objects should be in each set
dim_dict = {
1 : 10 ,
2 : 10 ,
3 : 7 ,
4 : 14
}
# minimized function: sum of means vy each split set
def min_func ( arr ):
indexes_dict = vec_to_indexes_dict ( arr )
means = [ np . mean ( Set [ val ]) for val in indexes_dict . values ()]
return sum ( means )
# zero vector with available set labels at random positions
start_solution = np . zeros ( Set . size , dtype = np . int8 )
labels_vec = counts_to_vec ( dim_dict )
start_solution [ np . random . choice ( Set_indexes , labels_vec . size , replace = False )] = labels_vec
def choice ( count = 3 ):
return np . random . choice ( Set_indexes , count , replace = False )
# mutation function
# temperature is the number cuz we will use only 1 cooling, but it's not necessary to use it)
def mut ( x_as_array , temperature_as_array_or_one_number ):
new_x_as_array = x_as_array . copy ()
# replace some values
while True :
inds = choice ()
if np . unique ( new_x_as_array [ inds ]). size == 1 : # there is no sense to replace same values
continue
new_x_as_array [ inds ] = new_x_as_array [ np . random . permutation ( inds )]
return new_x_as_array
# creating a model
model = SimulatedAnnealing ( min_func , Set_indexes . size )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80 ,
seed = SEED ,
reinit_from_best = True
)
model . plot_report ( save_as = 'best_split.png' )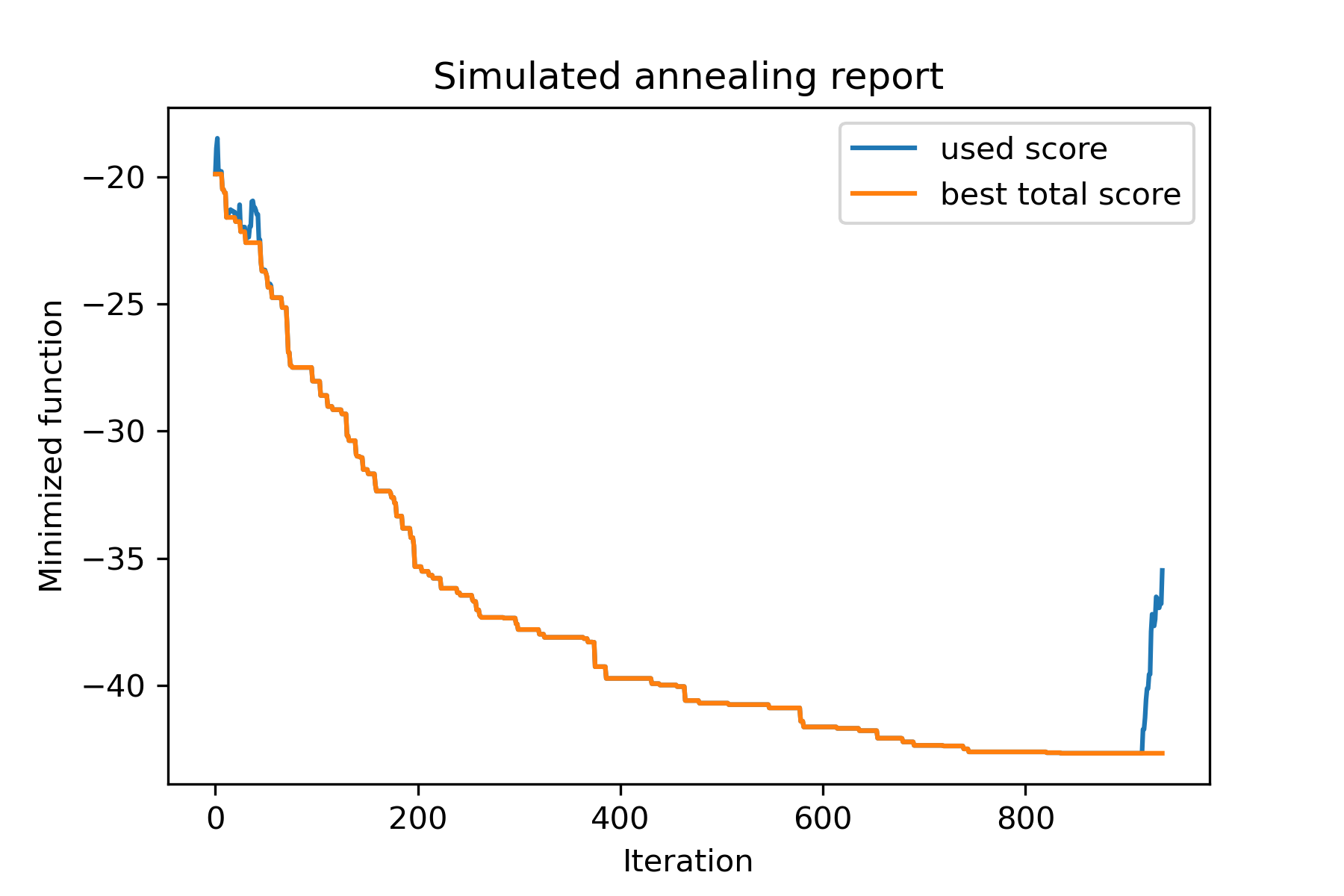
让我们尝试解决Berlin52任务的旅行推销员问题。在此任务中,有52个城市具有文件坐标。
首先,让我们进口包:
import math
import numpy as np
import pandas as pd
import matplotlib . pyplot as plt
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling设置种子以繁殖:
SEED = 1
np . random . seed ( SEED )读取坐标并创建距离矩阵:
# read coordinates
coords = pd . read_csv ( 'berlin52_coords.txt' , sep = ' ' , header = None , names = [ 'index' , 'x' , 'y' ])
# dim is equal to count of cities
dim = coords . shape [ 0 ]
# distance matrix
distances = np . empty (( dim , dim ))
for i in range ( dim ):
distances [ i , i ] = 0
for j in range ( i + 1 , dim ):
d = math . sqrt ( np . sum (( coords . iloc [ i , 1 :] - coords . iloc [ j , 1 :]) ** 2 ))
distances [ i , j ] = d
distances [ j , i ] = d创建随机启动解决方案:
indexes = np . arange ( dim )
# some start solution (indexes shuffle)
start_solution = np . random . choice ( indexes , dim , replace = False )定义一个计算长度长度的函数:
# minized function
def way_length ( arr ):
s = 0
for i in range ( 1 , dim ):
s += distances [ arr [ i - 1 ], arr [ i ]]
# also we should end the way in the beggining
s += distances [ arr [ - 1 ], arr [ 1 ]]
return s让我们可视化开始解决方案:
def plotData ( indices , title , save_as = None ):
# create a list of the corresponding city locations:
locs = [ coords . iloc [ i , 1 :] for i in indices ]
locs . append ( coords . iloc [ indices [ 0 ], 1 :])
# plot a line between each pair of consequtive cities:
plt . plot ( * zip ( * locs ), linestyle = '-' , color = 'blue' )
# plot the dots representing the cities:
plt . scatter ( coords . iloc [:, 1 ], coords . iloc [:, 2 ], marker = 'o' , s = 40 , color = 'red' )
plt . title ( title )
if not ( save_as is None ): plt . savefig ( save_as , dpi = 300 )
plt . show ()
# let's plot start solution
plotData ( start_solution , f'start random solution (score = { round ( way_length ( start_solution ), 2 ) } )' , 'salesman_start.png' )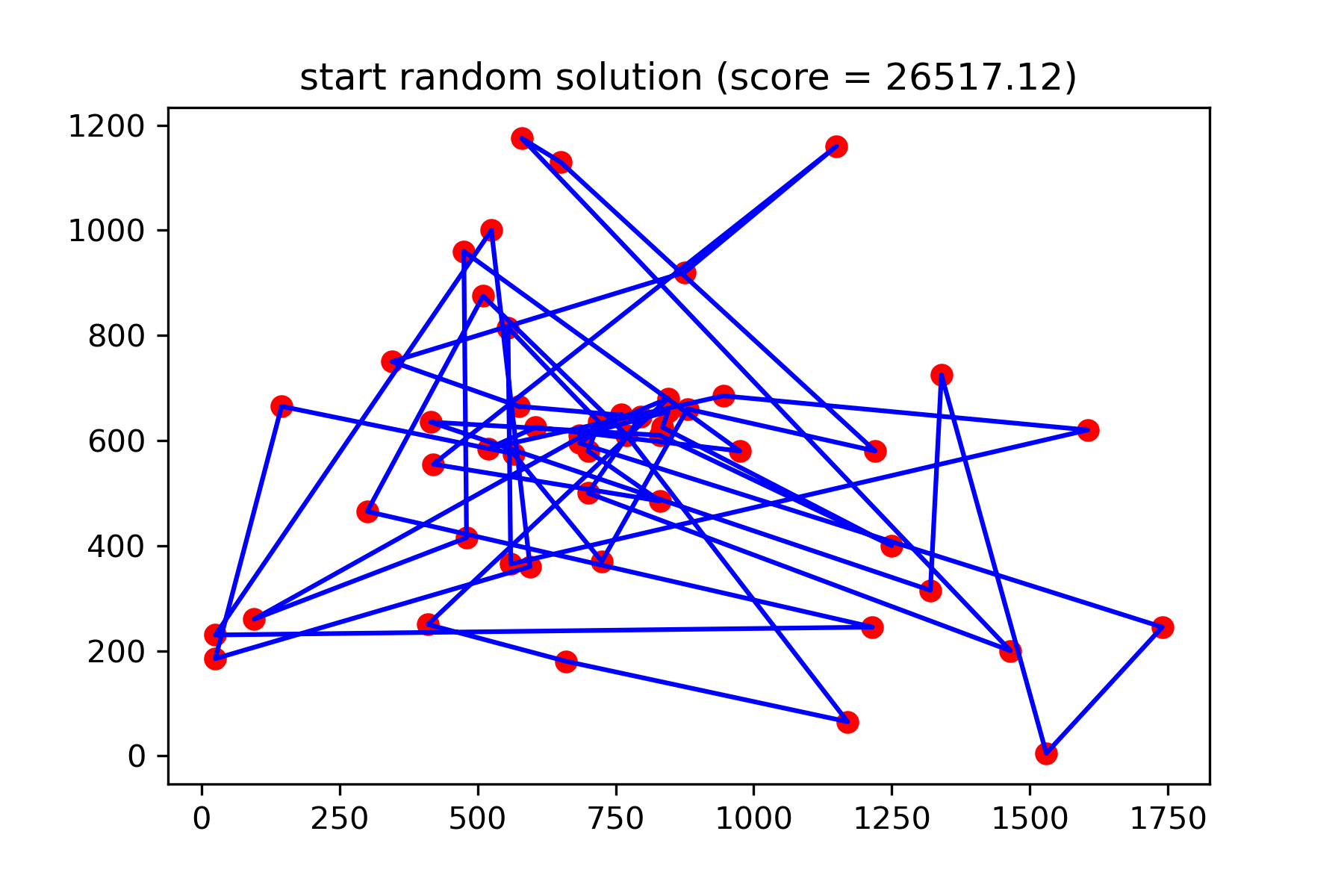
这真的不是很好的解决方案。我想为此任务创建此突变功能:
def mut ( x_as_array , temperature_as_array_or_one_number ):
# random indexes
rand_inds = np . random . choice ( indexes , 3 , replace = False )
# shuffled indexes
goes_to = np . random . permutation ( rand_inds )
# just replace some positions in the array
new_x_as_array = x_as_array . copy ()
new_x_as_array [ rand_inds ] = new_x_as_array [ goes_to ]
return new_x_as_array开始搜索:
# creating a model
model = SimulatedAnnealing ( way_length , dim )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 15000 ,
max_iterations_without_progress = 2000 ,
step_for_reinit_temperature = 80 ,
reinit_from_best = True ,
seed = SEED
)
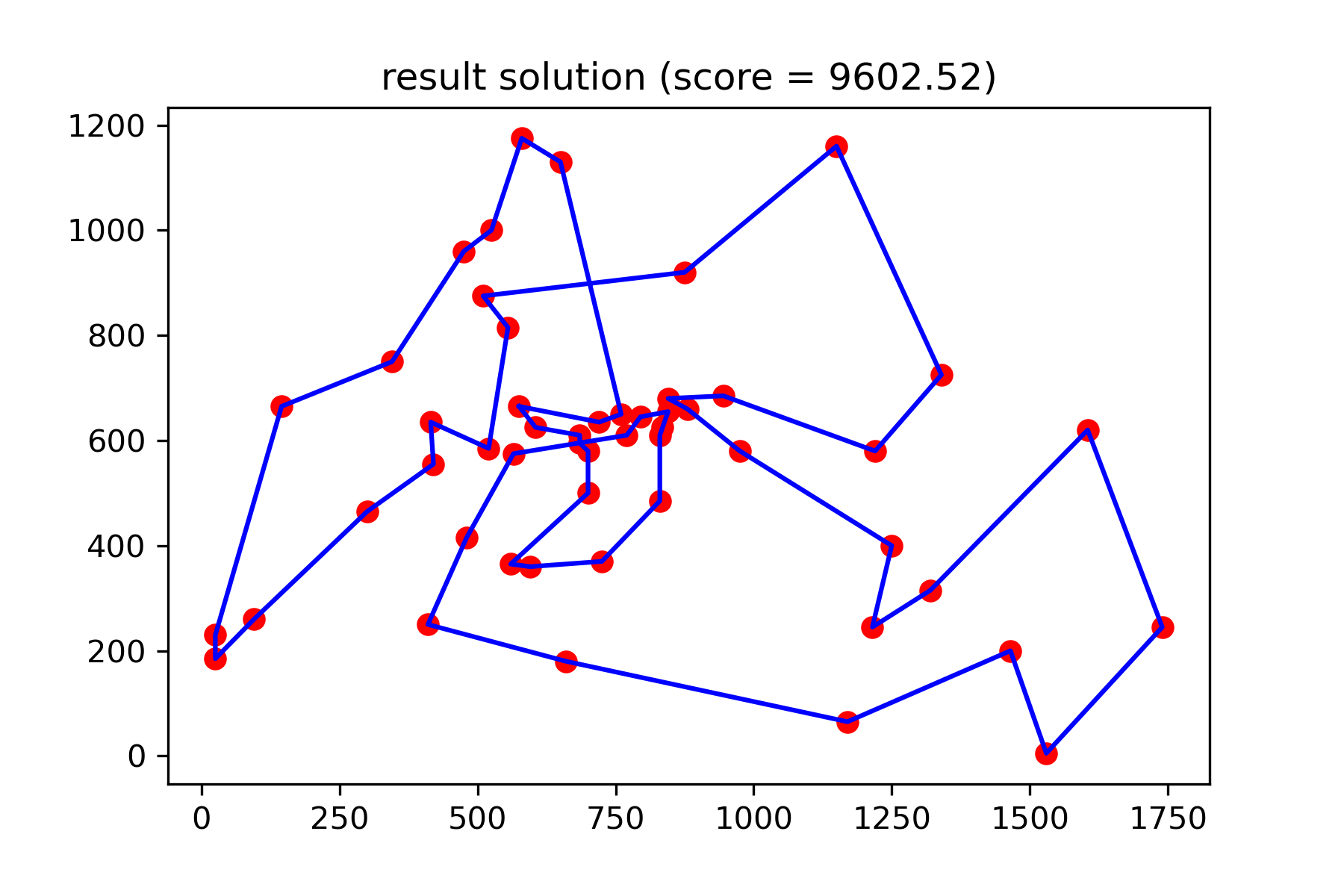
model . plot_report ( save_as = 'best_salesman.png' )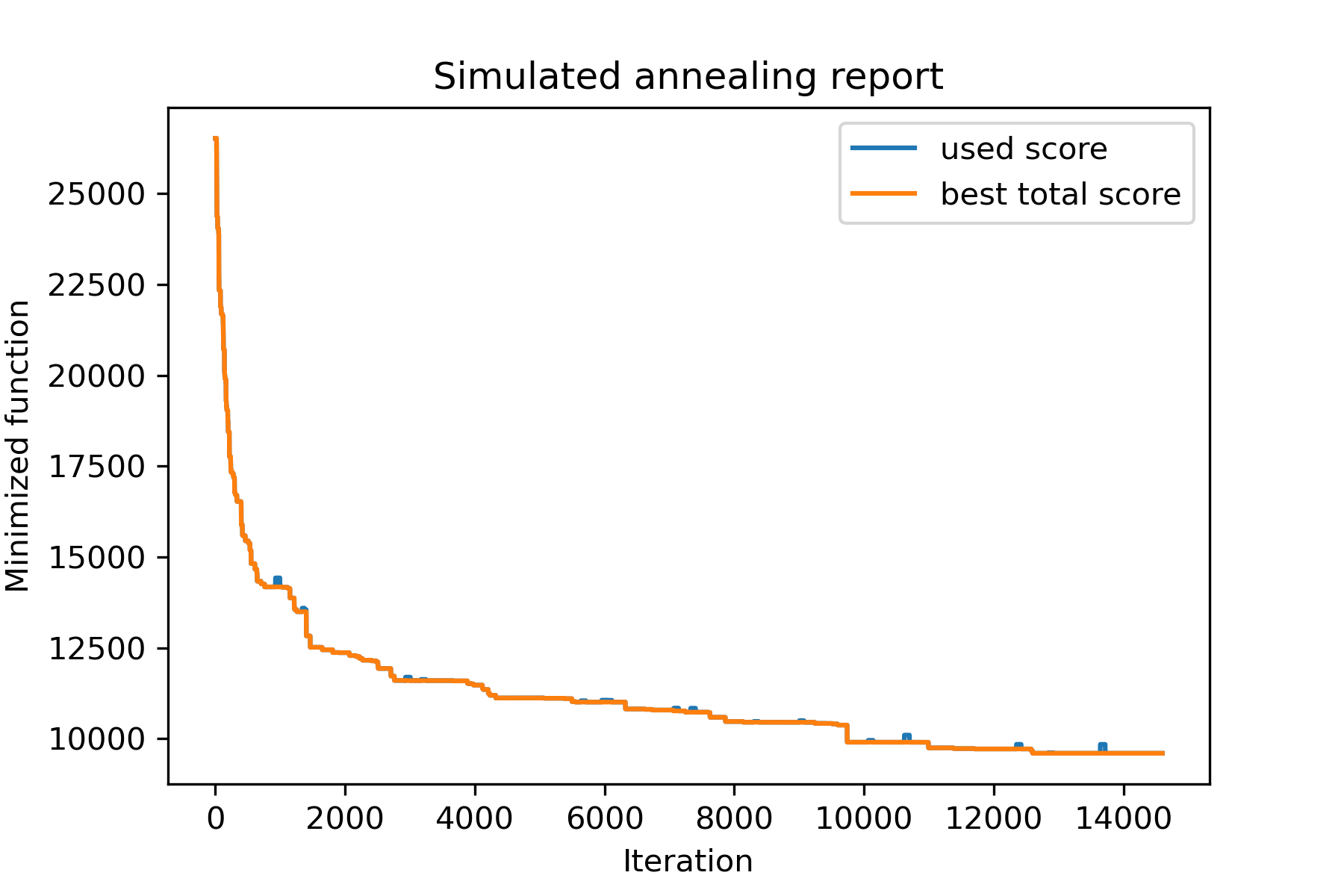
并看到我们更好的解决方案:
plotData ( best_solution , f'result solution (score = { round ( best_val , 2 ) } )' , 'salesman_result.png' )