시뮬레이션 된 어닐링 방법의 가장 간단한 구현 (DPEA)
pip install SimplestSimulatedAnnealing
이것은 기능 최소화를 위한 진화 알고리즘입니다.
단계 :
f 가 최소화되어야한다고 결정해야합니다x0 결정 (무작위 일 수 있음)mut 합니다. 이 함수는 x0 및 온도 T 에 대한 정보를 사용하여 새로운 (임의) x1 솔루션을 제공해야합니다.cooling 체제 선택 또는 생성 (온도 거동)Tx0 솔루션과 f(x0) Best Score가 있습니다.x1 = mut(x0) 만들고 f(x1) 계산합시다.f(x1) < f(x0) 인 경우 더 나은 솔루션 x0 = x1 발견했습니다. 그렇지 않으면 x1 로 x0 으로 대체 할 수 있습니다. 확률 exp((f(x0) - f(x1)) / T)cooling 기능을 사용하여 T 감소 : T = cooling(T)패키지 가져 오기 :
import math
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling , simple_continual_mutation최소화 된 기능 (rastrigin)을 결정합니다.
def Rastrigin ( arr ):
return 10 * arr . size + np . sum ( arr ** 2 ) - 10 * np . sum ( np . cos ( 2 * math . pi * arr ))
dim = 5우리는 가장 간단한 가우스 돌연변이를 사용할 것입니다.
mut = simple_continual_mutation ( std = 0.5 )모델 객체 생성 (기능 및 차원 설정) :
model = SimulatedAnnealing ( Rastrigin , dim )검색을 시작하고 보고서를 참조하십시오.
best_solution , best_val = model . run (
start_solution = np . random . uniform ( - 5 , 5 , dim ),
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80
)
model . plot_report ( save_as = 'simple_example.png' )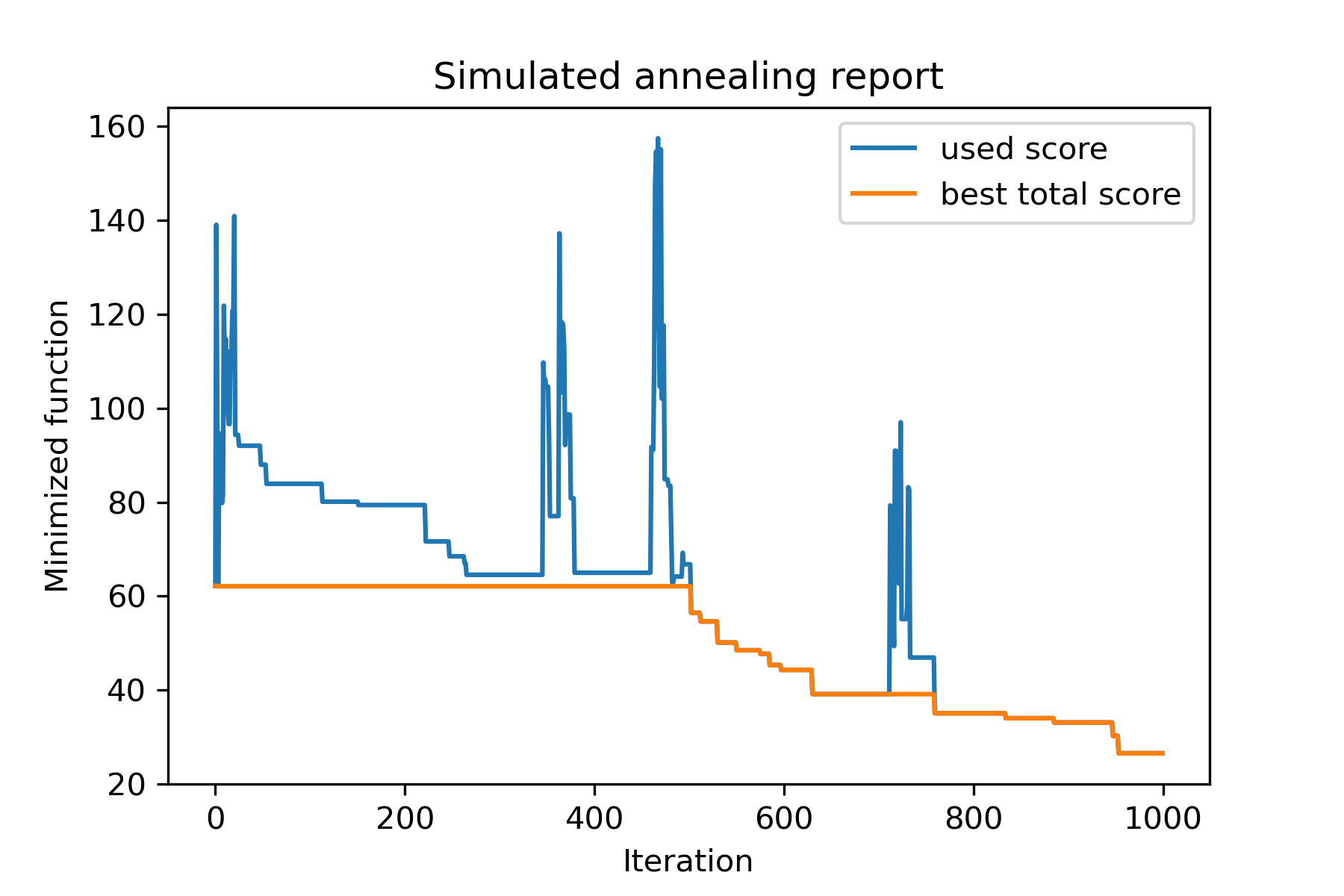
패키지의 주요 방법은 run() 입니다. 논쟁을 확인합시다.
model . run ( start_solution ,
mutation ,
cooling ,
start_temperature ,
max_function_evals = 1000 ,
max_iterations_without_progress = 250 ,
step_for_reinit_temperature = 90 ,
reinit_from_best = False ,
seed = None )어디:
start_solution : Numpy 배열; 시작 해야하는 솔루션.
mutation : 기능 (배열, 배열/번호). 기능
def mut ( x_as_array , temperature_as_array_or_one_number ):
# some code
return new_x_as_array이 기능은 기존에서 새로운 솔루션을 생성합니다. 참조하십시오
cooling : 냉각 기능 / 기능 목록. 냉각 기능 또는 목록 목록. 보다
start_temperature : 번호 또는 번호 배열 (목록/튜플). 온도를 시작하십시오. 숫자 또는 숫자 배열 일 수 있습니다.
max_function_evals : int, 선택 사항. 최대 기능 평가 수. 기본값은 1000입니다.
max_iterations_without_progress : int, 옵션. 글로벌 진보가없는 최대 반복 횟수. 기본값은 250입니다.
step_for_reinit_temperature : int, 선택 사항. 진보 온도가없는이 수의 반복 후에는 시작처럼 초기화됩니다. 기본값은 90입니다.
reinit_from_best : 부울, 선택 사항. 온도를 재발 한 후 최상의 솔루션 (또는 마지막 현재 솔루션)에서 알고리즘을 시작하십시오. 기본값은 False입니다.
seed : int/none, 선택 사항. 임의의 종자 (필요한 경우)
알고리즘의 중요한 부분은 냉각 기능 입니다. 이 함수는 온도 값을 전류 반복 숫자, 현재 온도 및 시작 온도에 따라 제어합니다. U는 패턴을 사용하여 나만의 냉각 기능을 만들 수 있습니다.
def func ( T_last , T0 , k ):
# some code
return T_new 여기서 T_last (int/float)는 이전 반복의 온도 값, T0 (int/float)은 시작 온도이고 k (int> 0)는 반복 횟수입니다. 이 정보 중 일부를 사용하여 새로운 온도 T_new 생성해야합니다.
양의 온도 만 생성하기 위해 기능을 구축하는 것이 좋습니다.
Cooling 클래스에는 몇 가지 냉각 기능이 있습니다.
Cooling.linear(mu, Tmin = 0.01)Cooling.exponential(alpha = 0.9)Cooling.reverse(beta = 0.0005)Cooling.logarithmic(c, d = 1) - 권장되지 않습니다Cooling.linear_reverse() u는 SimulatedAnnealing.plot_temperature 메소드를 사용하여 냉각 기능의 동작을 볼 수 있습니다. 몇 가지 예를 보자 :
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
# simplest way to set cooling regime
temperature = 100
cooling = Cooling . reverse ( beta = 0.001 )
# we can temperature behaviour using this code
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse.png' )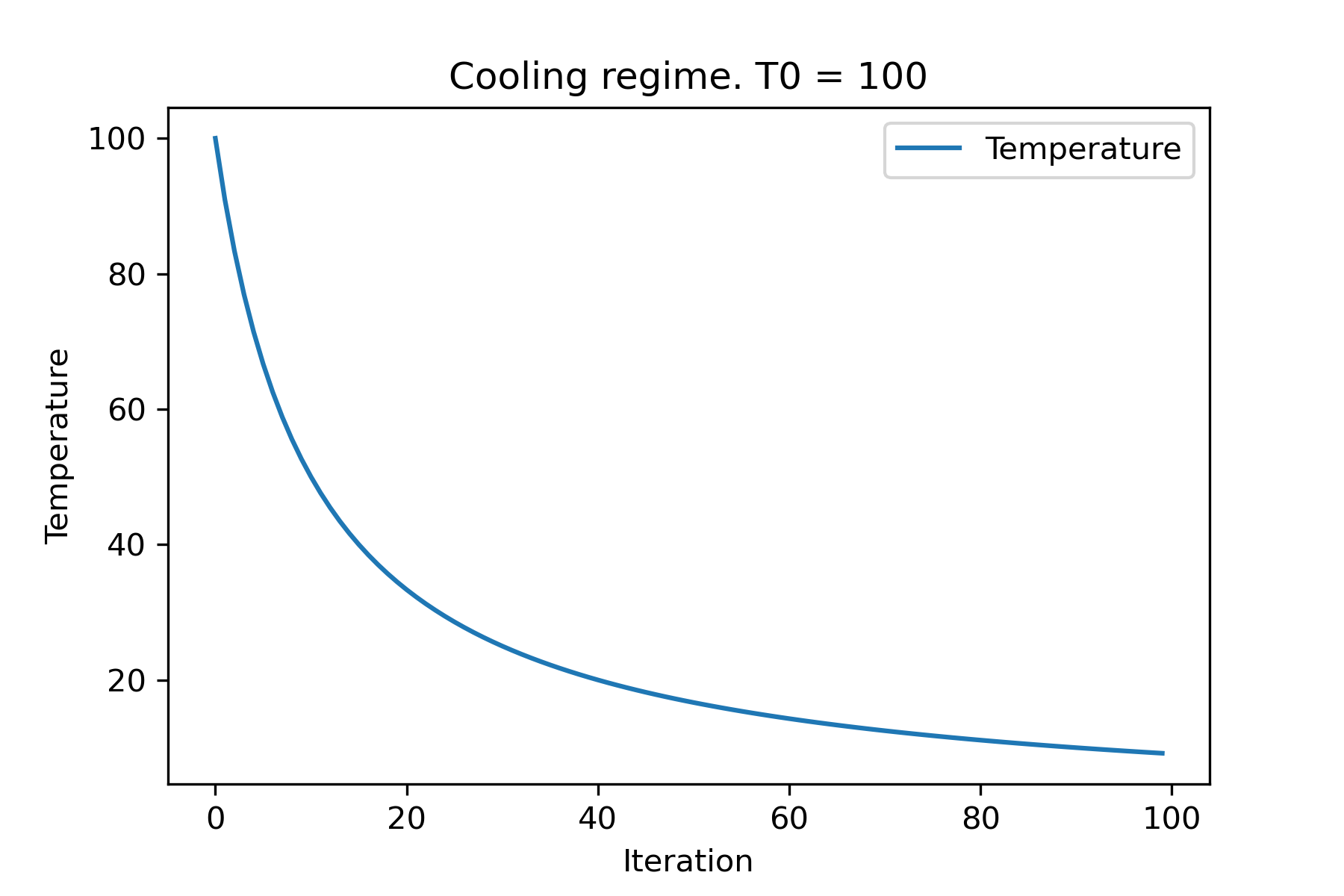
# we can set several temparatures (for each dimention)
temperature = [ 150 , 100 , 50 ]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse_diff_temp.png' )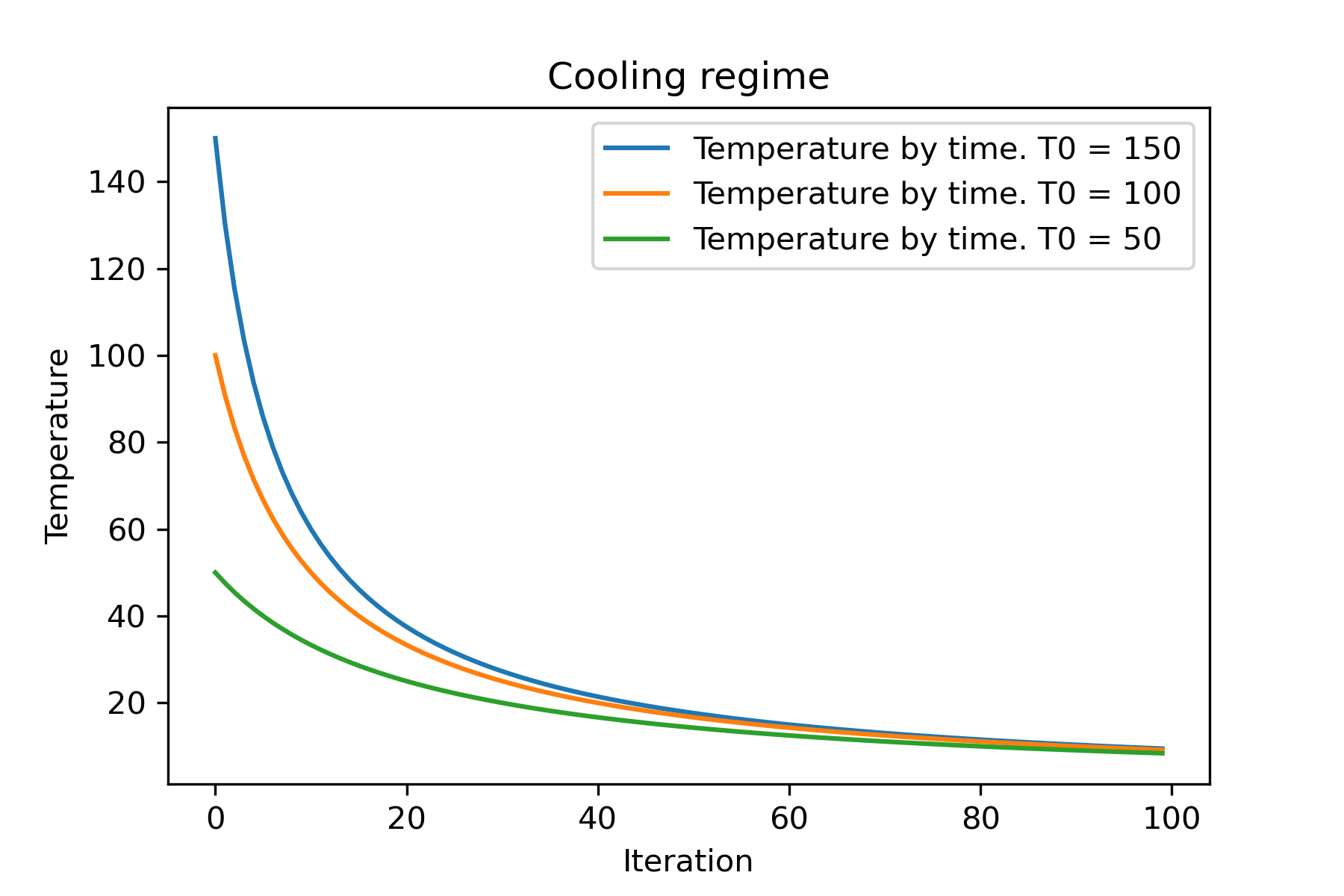
# or several coolings (for each dimention)
temperature = 100
cooling = [
Cooling . reverse ( beta = 0.0001 ),
Cooling . reverse ( beta = 0.0005 ),
Cooling . reverse ( beta = 0.001 )
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse_diff_beta.png' )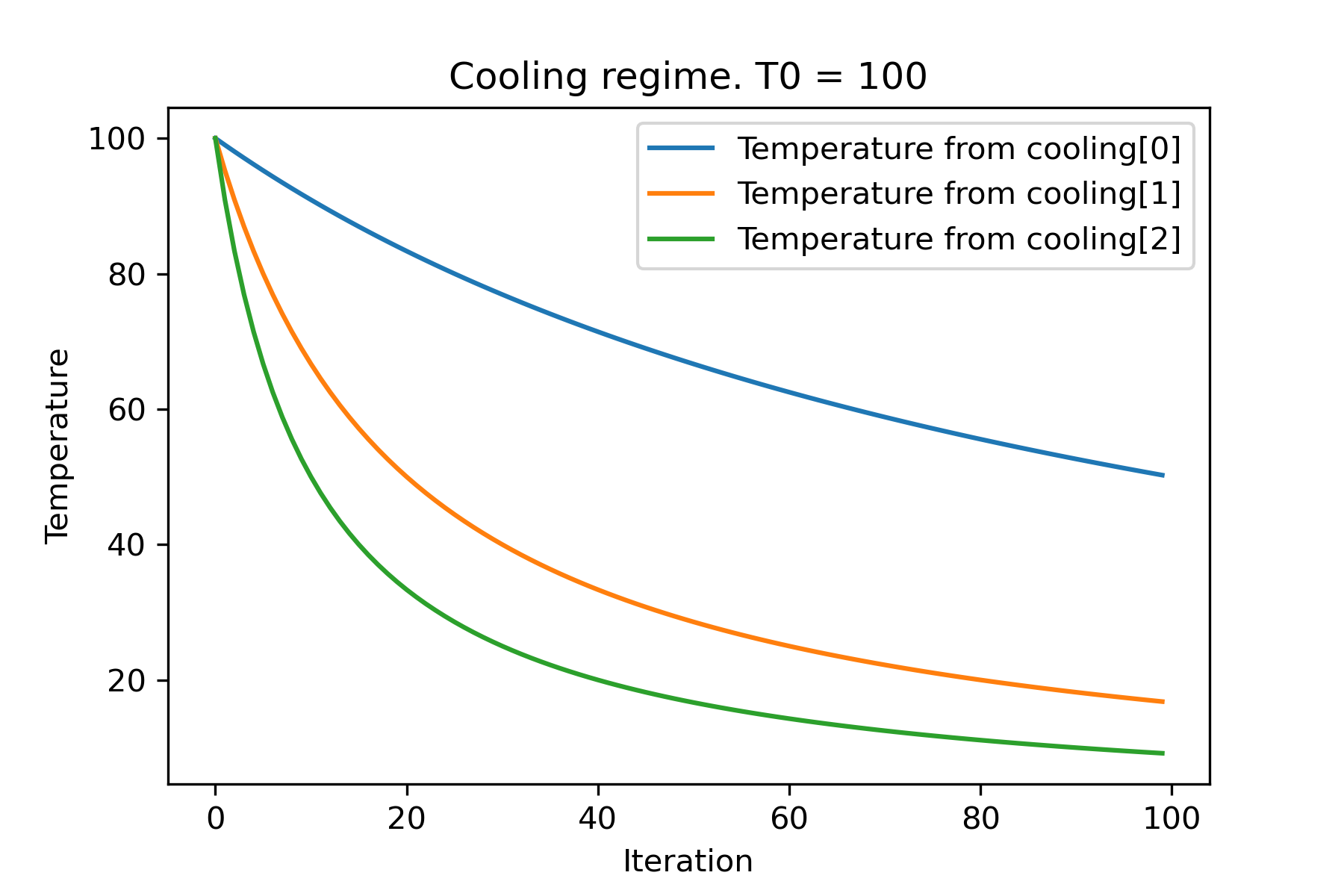
# all supported coolling regimes
temperature = 100
cooling = [
Cooling . linear ( mu = 1 ),
Cooling . reverse ( beta = 0.0007 ),
Cooling . exponential ( alpha = 0.85 ),
Cooling . linear_reverse (),
Cooling . logarithmic ( c = 100 , d = 1 )
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'diff_temp.png' )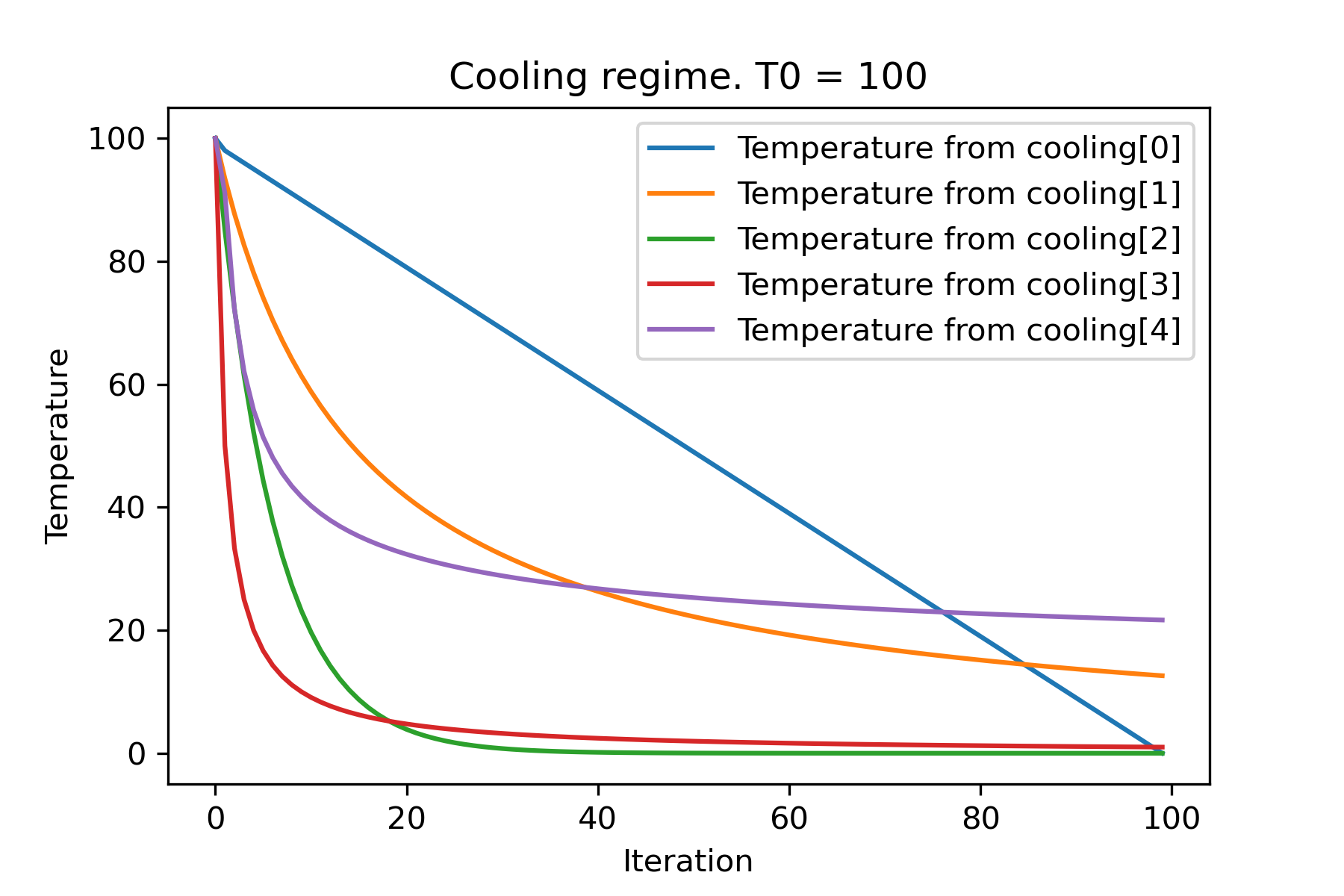
# and we can set own temperature and cooling for each dimention!
temperature = [ 100 , 125 , 150 ]
cooling = [
Cooling . exponential ( alpha = 0.85 ),
Cooling . exponential ( alpha = 0.9 ),
Cooling . exponential ( alpha = 0.95 ),
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'diff_temp_and_cool.png' )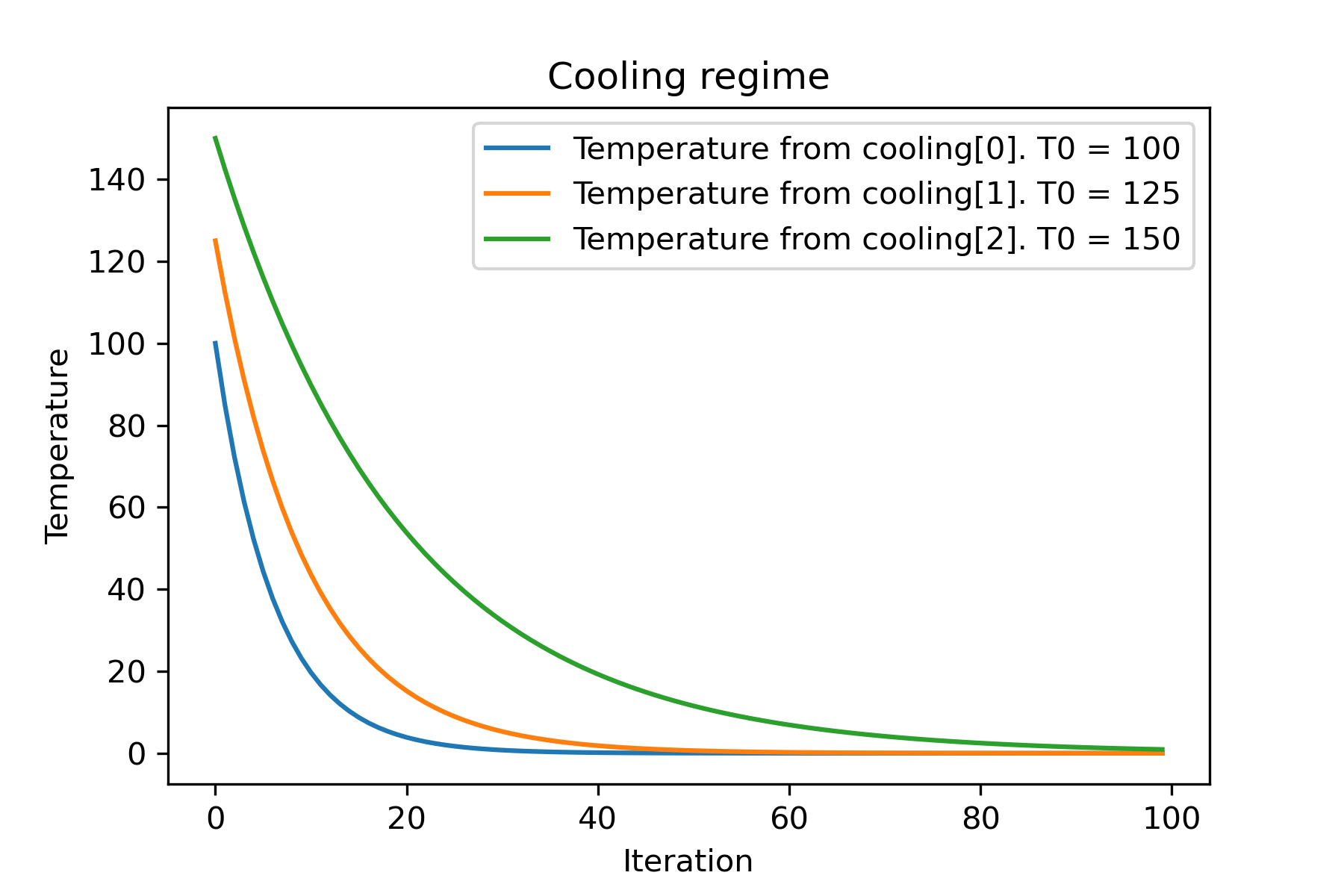
왜 그렇게 많은 냉각 체제가 있습니까? 어떤 일을 위해 그들 중 하나는 그렇게 나을 수 있습니다! 이 스크립트에서는 방해 기능을 위해 다른 냉각을 테스트 할 수 있습니다.
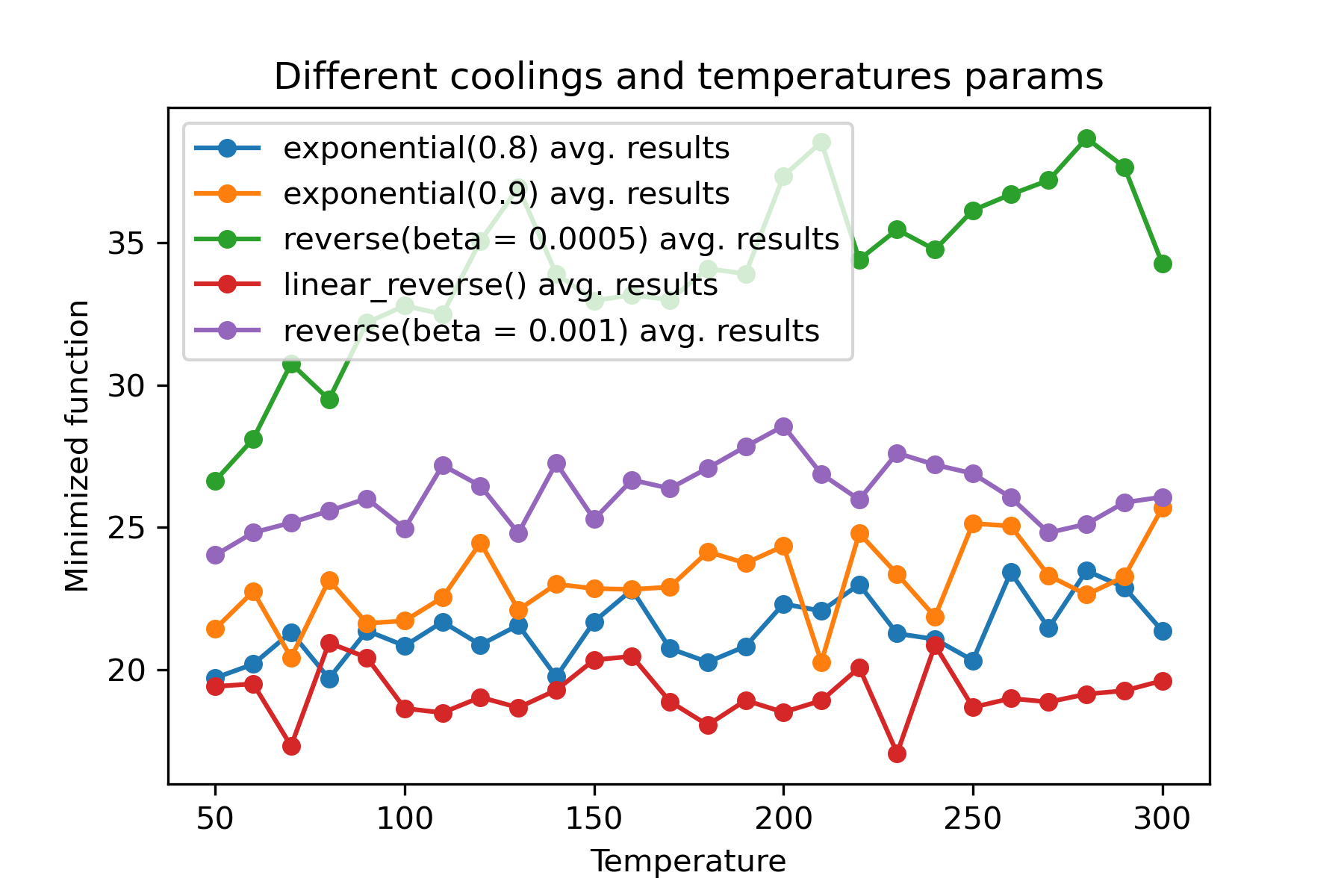
각 차원에 대해 다른 냉각을 사용하고 온도를 시작하는 것은 놀라운 기능입니다.
import math
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling , simple_continual_mutation
def Rastrigin ( arr ):
return 10 * arr . size + np . sum ( arr ** 2 ) - 10 * np . sum ( np . cos ( 2 * math . pi * arr ))
dim = 5
model = SimulatedAnnealing ( Rastrigin , dim )
best_solution , best_val = model . run (
start_solution = np . random . uniform ( - 5 , 5 , dim ),
mutation = simple_continual_mutation ( std = 1 ),
cooling = [ # different cooling for each dimention
Cooling . exponential ( 0.8 ),
Cooling . exponential ( 0.9 ),
Cooling . reverse ( beta = 0.0005 ),
Cooling . linear_reverse (),
Cooling . reverse ( beta = 0.001 )
],
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 250 ,
step_for_reinit_temperature = 90 ,
reinit_from_best = False
)
print ( best_val )
model . plot_report ( save_as = 'different_coolings.png' )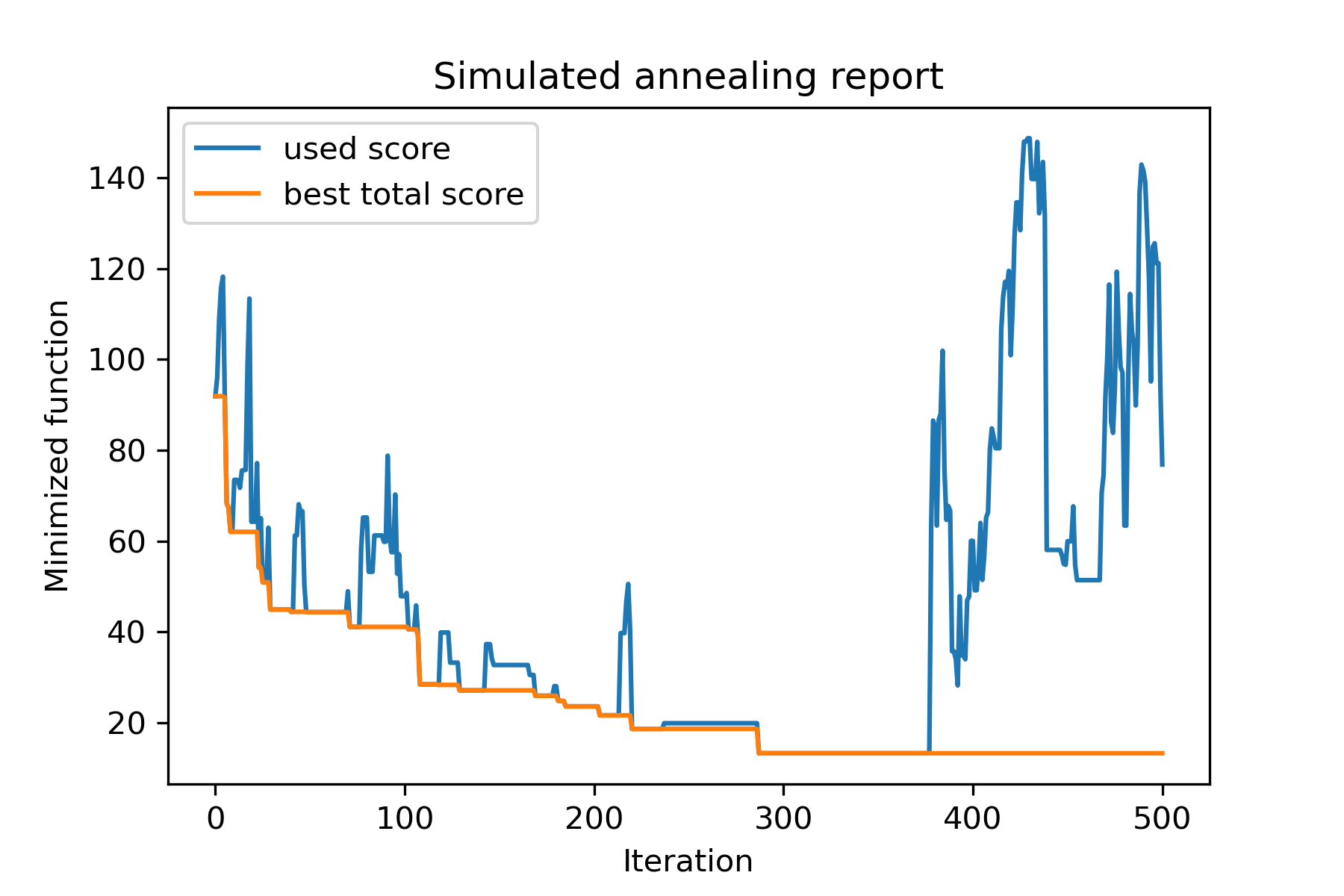
여러 냉각을 사용하는 주된 이유는 각 차원의 지정 동작입니다. 예를 들어, 공간의 1 차원은 2 차원보다 훨씬 넓을 수 있으므로 1 차원을 더 넓은 검색하는 것이 좋습니다. U는 다른 start temperatures 사용하고 다른 coolings 사용하여 특수한 mut 기능을 사용하여 생산할 수 있습니다.
다중 냉각을 사용하는 또 다른 이유는 선택 방법입니다. 각 차원마다 좋은 솔루션과 나쁜 솔루션 사이의 여러 냉각 선택의 경우 각 차원마다 적용됩니다 . 따라서 더 나은 솔루션을 찾을 가능성이 높아집니다.
돌연변이 기능은 가장 중요한 매개 변수입니다. 현재 객체 및 온도에 대한 정보를 사용하여 새 개체를 만드는 동작을 결정합니다. mut 기능을 만들 때 이러한 원칙을 계산하는 것이 좋습니다.
mut 의 구조를 기억합시다 :
def mut ( x_as_array , temperature_as_array_or_one_number ):
# some code
return new_x_as_array 여기서 x_as_array 는 현재 솔루션이며 new_x_as_array 돌연변이 된 솔루션입니다 (무작위와 같은 어둡습니다. 또한 temperature_as_array_or_one_number Multicooling이 아닌 솔루션의 경우에만 숫자 라는 것을 기억해야합니다. 그렇지 않으면 (여러 냉각 또는 둘 다의 몇 가지 시작 온도를 사용할 때)는 멍청한 어레이 입니다. 예를 참조하십시오
이 예에서는 일부 기능을 최소화하는 n 객체로 세트에서 k 객체를 선택하는 방법을 보여줍니다 (이 예에서는 중앙값의 절대 값) :
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
SEED = 3
np . random . seed ( SEED )
Set = np . random . uniform ( low = - 15 , high = 5 , size = 100 ) # all set
dim = 10 # how many objects should we choose
indexes = np . arange ( Set . size )
# minimized function -- subset with best |median|
def min_func ( arr ):
return abs ( np . median ( Set [ indexes [ arr . astype ( bool )]]))
# zero vectors with 'dim' ones at random positions
start_solution = np . zeros ( Set . size )
start_solution [ np . random . choice ( indexes , dim , replace = False )] = 1
# mutation function
# temperature is the number cuz we will use only 1 cooling, but it's not necessary to use it)
def mut ( x_as_array , temperature_as_array_or_one_number ):
mask_one = x_as_array == 1
mask_zero = np . logical_not ( mask_one )
new_x_as_array = x_as_array . copy ()
# replace some zeros with ones
new_x_as_array [ np . random . choice ( indexes [ mask_one ], 1 , replace = False )] = 0
new_x_as_array [ np . random . choice ( indexes [ mask_zero ], 1 , replace = False )] = 1
return new_x_as_array
# creating a model
model = SimulatedAnnealing ( min_func , dim )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80 ,
seed = SEED
)
model . plot_report ( save_as = 'best_subset.png' )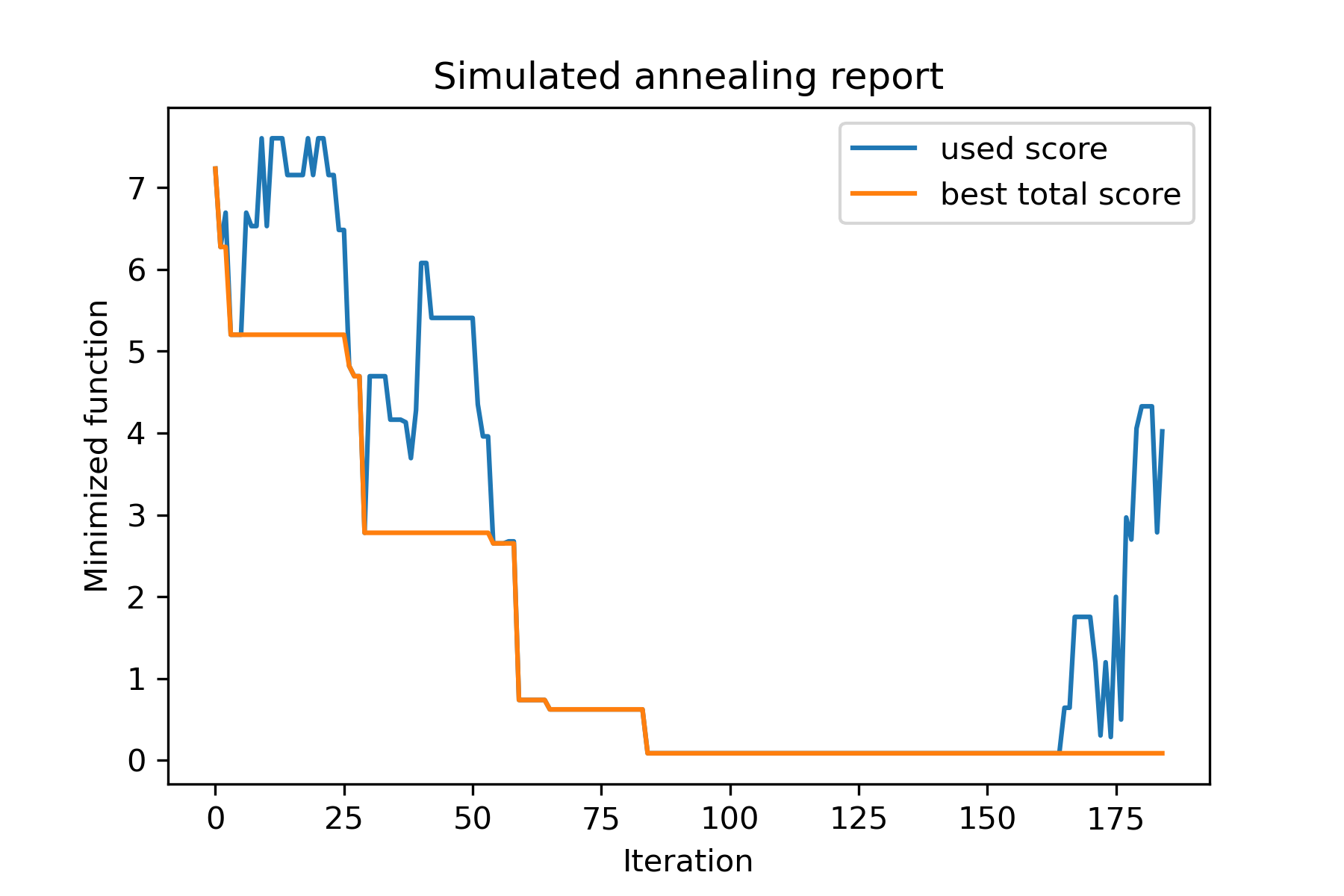
이 작업을 살펴 보겠습니다.
split set of values {v1, v2, v3, ..., vn} to sets 0, 1, 2, 3
with their sizes (volumes determined by user) to complete best sets metric
그것을 해결하는 방법 중 하나 :
from collections import defaultdict
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
################### useful methods
def counts_to_vec ( dic_count ):
"""
converts dictionary like {1: 3, 2: 4}
to array [1, 1, 1, 2, 2, 2, 2]
"""
arrs = [ np . full ( val , fill_value = key ) for key , val in dic_count . items ()]
return np . concatenate ( tuple ( arrs ))
def vec_to_indexes_dict ( vector ):
"""
converts vector like [1, 0, 1, 2, 2]
to dictionary with indexes {1: [0, 2], 2: [3, 4]}
"""
res = defaultdict ( list )
for i , v in enumerate ( vector ):
res [ v ]. append ( i )
return { int ( key ): np . array ( val ) for key , val in res . items () if key != 0 }
#################### START PARAMS
SEED = 3
np . random . seed ( SEED )
Set = np . random . uniform ( low = - 15 , high = 5 , size = 100 ) # all set
Set_indexes = np . arange ( Set . size )
# how many objects should be in each set
dim_dict = {
1 : 10 ,
2 : 10 ,
3 : 7 ,
4 : 14
}
# minimized function: sum of means vy each split set
def min_func ( arr ):
indexes_dict = vec_to_indexes_dict ( arr )
means = [ np . mean ( Set [ val ]) for val in indexes_dict . values ()]
return sum ( means )
# zero vector with available set labels at random positions
start_solution = np . zeros ( Set . size , dtype = np . int8 )
labels_vec = counts_to_vec ( dim_dict )
start_solution [ np . random . choice ( Set_indexes , labels_vec . size , replace = False )] = labels_vec
def choice ( count = 3 ):
return np . random . choice ( Set_indexes , count , replace = False )
# mutation function
# temperature is the number cuz we will use only 1 cooling, but it's not necessary to use it)
def mut ( x_as_array , temperature_as_array_or_one_number ):
new_x_as_array = x_as_array . copy ()
# replace some values
while True :
inds = choice ()
if np . unique ( new_x_as_array [ inds ]). size == 1 : # there is no sense to replace same values
continue
new_x_as_array [ inds ] = new_x_as_array [ np . random . permutation ( inds )]
return new_x_as_array
# creating a model
model = SimulatedAnnealing ( min_func , Set_indexes . size )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80 ,
seed = SEED ,
reinit_from_best = True
)
model . plot_report ( save_as = 'best_split.png' )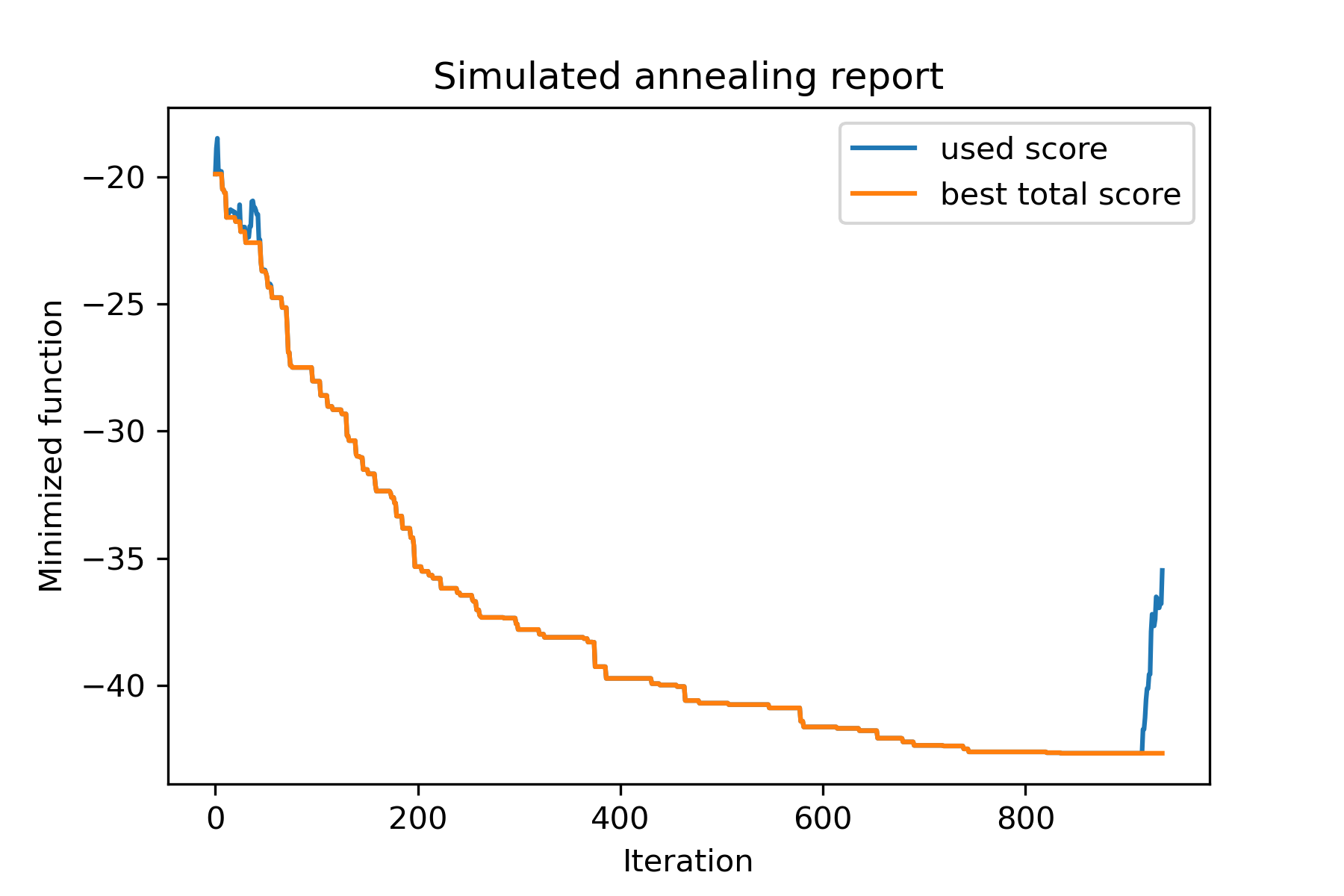
Berlin52 작업을 위해 여행 세일즈맨 문제를 해결해 봅시다. 이 작업에는 파일의 좌표가있는 52 개 도시가 있습니다.
먼저 패키지를 가져 오자 :
import math
import numpy as np
import pandas as pd
import matplotlib . pyplot as plt
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling재현을위한 씨앗 설정 :
SEED = 1
np . random . seed ( SEED )좌표를 읽고 거리 매트릭스 생성 :
# read coordinates
coords = pd . read_csv ( 'berlin52_coords.txt' , sep = ' ' , header = None , names = [ 'index' , 'x' , 'y' ])
# dim is equal to count of cities
dim = coords . shape [ 0 ]
# distance matrix
distances = np . empty (( dim , dim ))
for i in range ( dim ):
distances [ i , i ] = 0
for j in range ( i + 1 , dim ):
d = math . sqrt ( np . sum (( coords . iloc [ i , 1 :] - coords . iloc [ j , 1 :]) ** 2 ))
distances [ i , j ] = d
distances [ j , i ] = d무작위 시작 솔루션 생성 :
indexes = np . arange ( dim )
# some start solution (indexes shuffle)
start_solution = np . random . choice ( indexes , dim , replace = False )길이를 계산하는 함수를 정의하십시오.
# minized function
def way_length ( arr ):
s = 0
for i in range ( 1 , dim ):
s += distances [ arr [ i - 1 ], arr [ i ]]
# also we should end the way in the beggining
s += distances [ arr [ - 1 ], arr [ 1 ]]
return s시작 솔루션을 시각화합시다 :
def plotData ( indices , title , save_as = None ):
# create a list of the corresponding city locations:
locs = [ coords . iloc [ i , 1 :] for i in indices ]
locs . append ( coords . iloc [ indices [ 0 ], 1 :])
# plot a line between each pair of consequtive cities:
plt . plot ( * zip ( * locs ), linestyle = '-' , color = 'blue' )
# plot the dots representing the cities:
plt . scatter ( coords . iloc [:, 1 ], coords . iloc [:, 2 ], marker = 'o' , s = 40 , color = 'red' )
plt . title ( title )
if not ( save_as is None ): plt . savefig ( save_as , dpi = 300 )
plt . show ()
# let's plot start solution
plotData ( start_solution , f'start random solution (score = { round ( way_length ( start_solution ), 2 ) } )' , 'salesman_start.png' )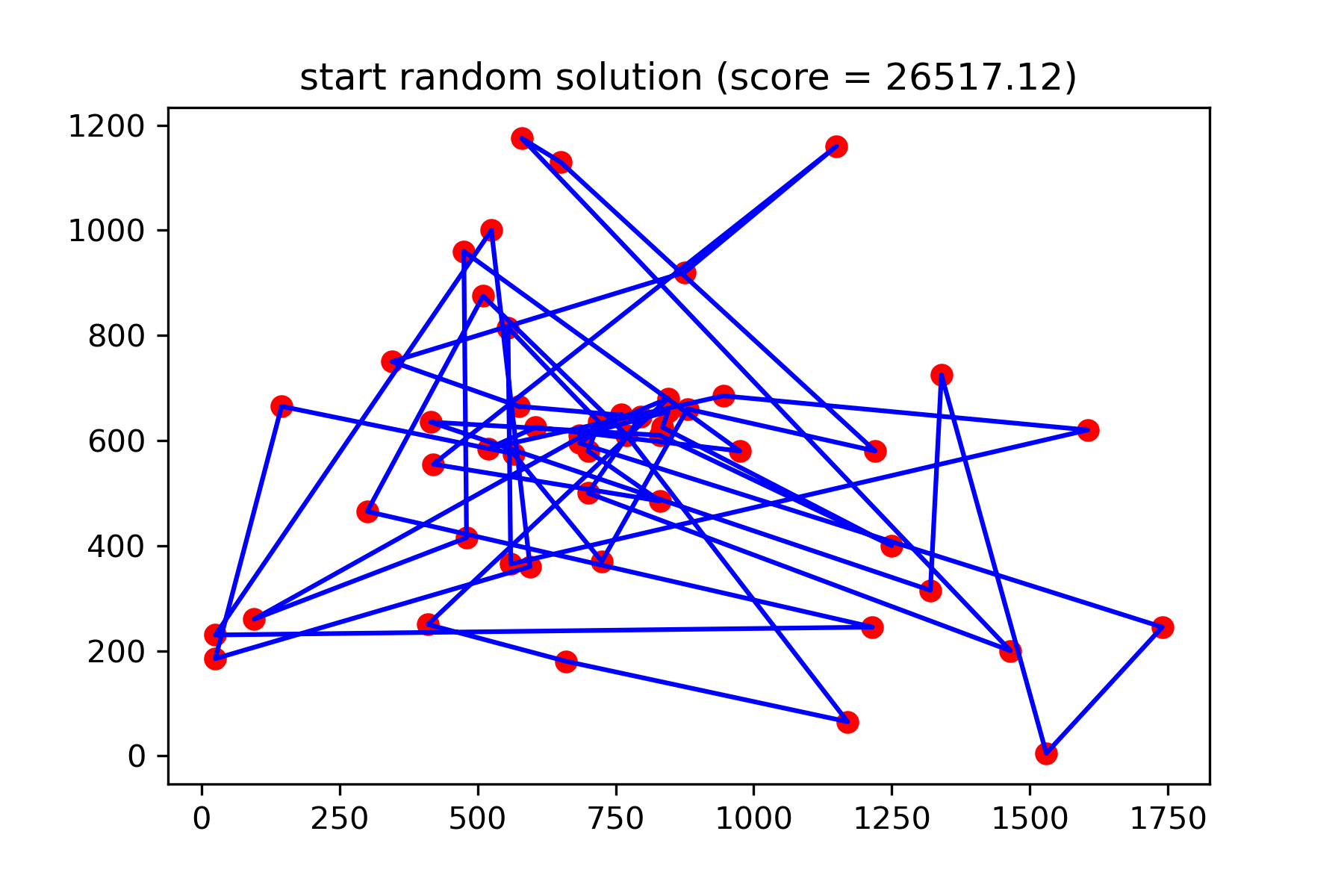
정말 좋은 해결책이 아닙니다. 이 작업을 위해이 돌연변이 기능을 만들고 싶습니다.
def mut ( x_as_array , temperature_as_array_or_one_number ):
# random indexes
rand_inds = np . random . choice ( indexes , 3 , replace = False )
# shuffled indexes
goes_to = np . random . permutation ( rand_inds )
# just replace some positions in the array
new_x_as_array = x_as_array . copy ()
new_x_as_array [ rand_inds ] = new_x_as_array [ goes_to ]
return new_x_as_array검색 시작 :
# creating a model
model = SimulatedAnnealing ( way_length , dim )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 15000 ,
max_iterations_without_progress = 2000 ,
step_for_reinit_temperature = 80 ,
reinit_from_best = True ,
seed = SEED
)
model . plot_report ( save_as = 'best_salesman.png' )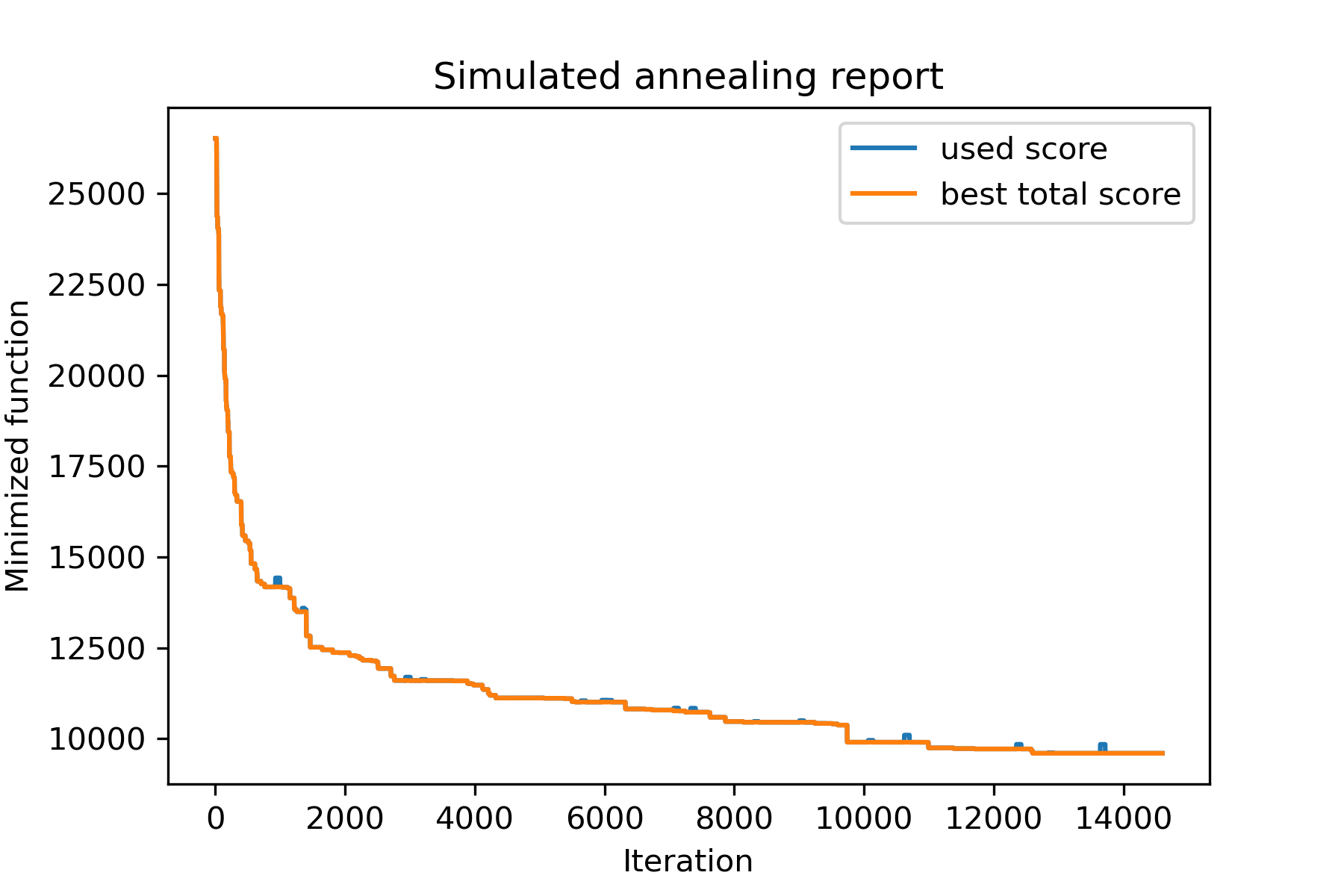
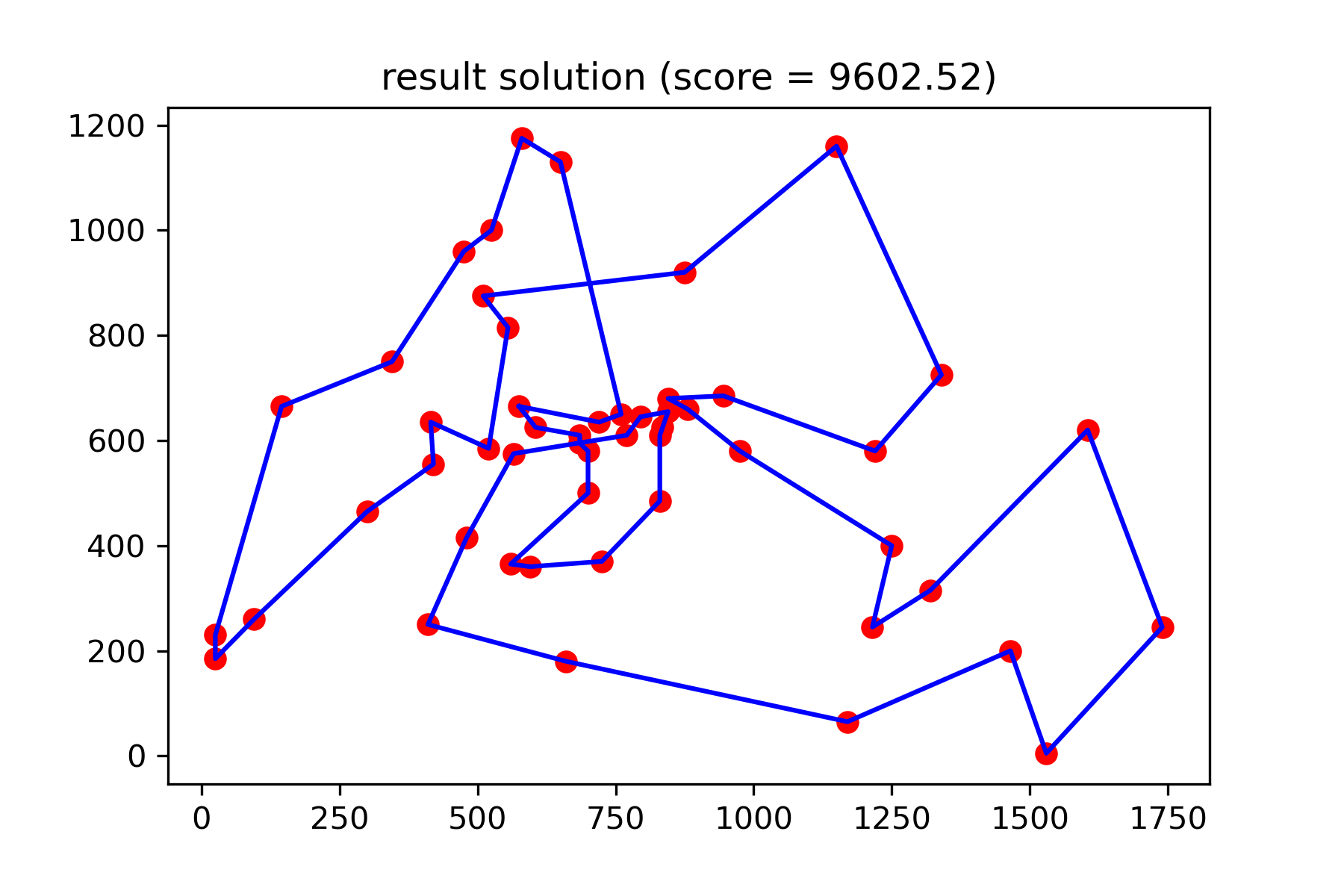
그리고 우리의 훨씬 더 나은 해결책을보십시오.
plotData ( best_solution , f'result solution (score = { round ( best_val , 2 ) } )' , 'salesman_result.png' )