La mise en œuvre la plus simple (à partir de DPEA) de la méthode de recuit simulé
pip install SimplestSimulatedAnnealing
Il s'agit de l'algorithme évolutif pour la minimisation des fonctions .
Mesures:
f doit être minimiséex0 (peut être aléatoire)mut . Cette fonction doit donner une nouvelle solution x1 (peut être aléatoire) en utilisant des informations sur x0 et la température T .cooling (comportement de température)Tx0 et le meilleur score f(x0)x1 = mut(x0) et calculons f(x1)f(x1) < f(x0) , nous avons trouvé une meilleure solution x0 = x1 . Sinon, nous pouvons remplacer x1 par x0 par une probabilité égale exp((f(x0) - f(x1)) / T)T en utilisant la fonction cooling : T = cooling(T)Packages d'importation:
import math
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling , simple_continual_mutationDéterminer la fonction minimisée (Rastrigin):
def Rastrigin ( arr ):
return 10 * arr . size + np . sum ( arr ** 2 ) - 10 * np . sum ( np . cos ( 2 * math . pi * arr ))
dim = 5Nous utiliserons la mutation de Gauss la plus simple:
mut = simple_continual_mutation ( std = 0.5 )Créer un objet modèle (définir la fonction et la dimension):
model = SimulatedAnnealing ( Rastrigin , dim )Commencez à rechercher et voir le rapport:
best_solution , best_val = model . run (
start_solution = np . random . uniform ( - 5 , 5 , dim ),
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80
)
model . plot_report ( save_as = 'simple_example.png' )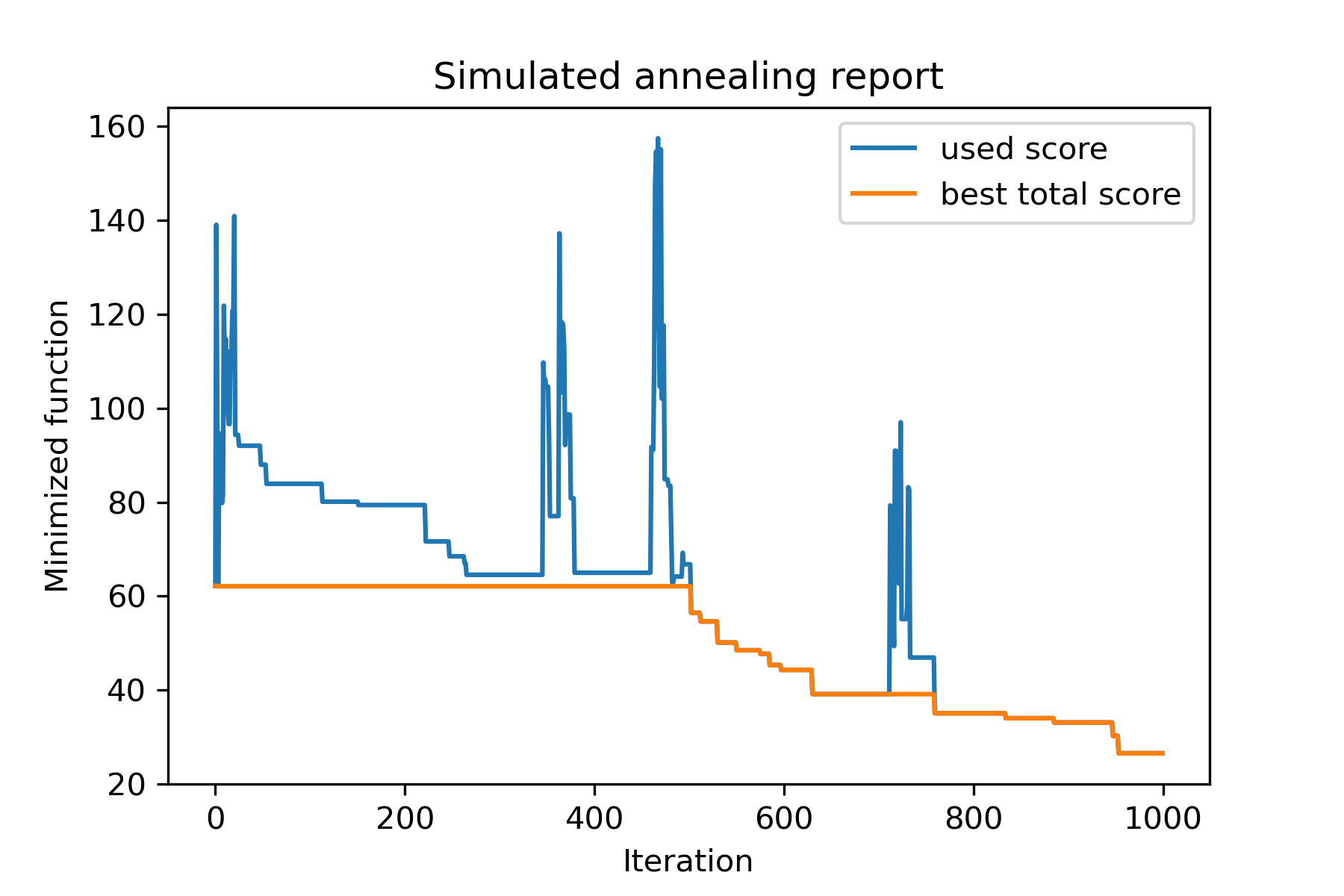
La méthode principale du package est run() . Vérifions ses arguments:
model . run ( start_solution ,
mutation ,
cooling ,
start_temperature ,
max_function_evals = 1000 ,
max_iterations_without_progress = 250 ,
step_for_reinit_temperature = 90 ,
reinit_from_best = False ,
seed = None )Où:
start_solution : Array Numpy; solution à partir de laquelle il devrait commencer.
mutation : fonction (tableau, tableau / numéro). Fonction comme
def mut ( x_as_array , temperature_as_array_or_one_number ):
# some code
return new_x_as_arrayCette fonction créera de nouvelles solutions à partir de l'existence. Voir aussi
cooling : liste de fonctions de refroidissement / fonctions. Fonction de refroidissement ou une liste de celles. Voir
start_temperature : numéro ou numéro de numéro (liste / tuple). Démarrez les températures. Peut être un numéro ou un tableau de nombres.
max_function_evals : int, facultatif. Nombre maximum d'évaluations de fonctions. La valeur par défaut est 1000.
max_iterations_without_progress : int, facultatif. Nombre maximum d'itérations sans progrès mondial. La valeur par défaut est 250.
step_for_reinit_temperature : int, facultatif. Une fois ce nombre d'itérations sans les températures de progression sera initialisée comme comme démarrage. La valeur par défaut est 90.
reinit_from_best : booléen, facultatif. L'algorithme de démarrage à partir de la meilleure solution après les températures de réintention (ou de la dernière solution de courant). La valeur par défaut est fausse.
seed : INT / None, facultatif. Graines aléatoires (si nécessaire)
La partie importante de l'algorithme est la fonction de refroidissement . Cette fonction contrôle la valeur de la température dépend du nombre d'itération de courant, de la température du courant et de la température de démarrage. Vous pouvez créer votre propre fonction de refroidissement en utilisant le motif:
def func ( T_last , T0 , k ):
# some code
return T_new Ici, T_last (int / float) est la valeur de température de l'itération précédente, T0 (int / float) est la température de démarrage et k (int> 0) est le nombre d'itération. Vous devez utiliser certaines de ces informations pour créer une nouvelle température T_new .
Il est fortement recommandé de construire votre fonction pour ne créer qu'une température positive.
En classe Cooling , il existe plusieurs fonctions de refroidissement:
Cooling.linear(mu, Tmin = 0.01)Cooling.exponential(alpha = 0.9)Cooling.reverse(beta = 0.0005)Cooling.logarithmic(c, d = 1) - Non recommandéCooling.linear_reverse() U peut voir le comportement de la fonction de refroidissement en utilisant la méthode SimulatedAnnealing.plot_temperature . Voyons plusieurs exemples:
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
# simplest way to set cooling regime
temperature = 100
cooling = Cooling . reverse ( beta = 0.001 )
# we can temperature behaviour using this code
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse.png' )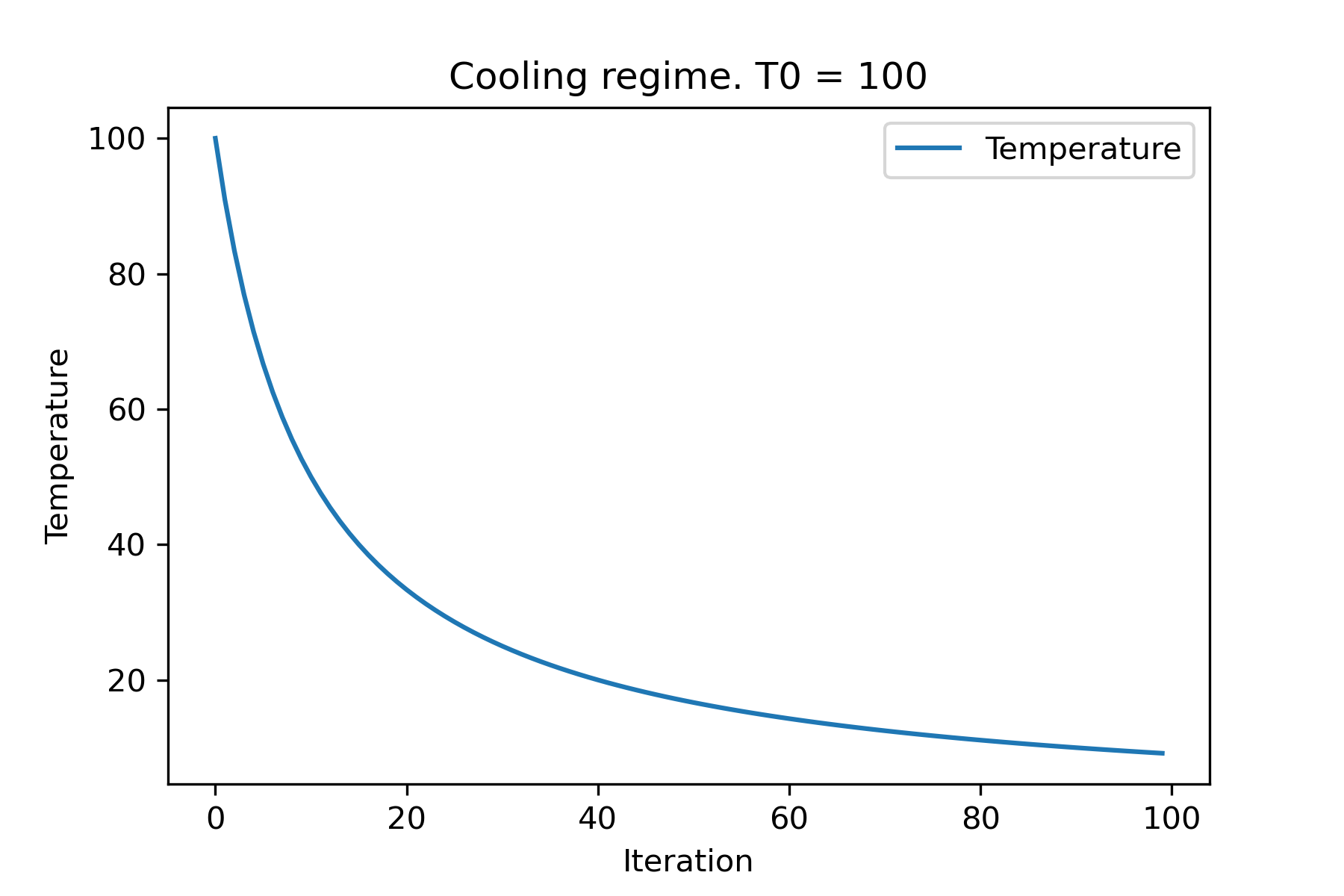
# we can set several temparatures (for each dimention)
temperature = [ 150 , 100 , 50 ]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse_diff_temp.png' )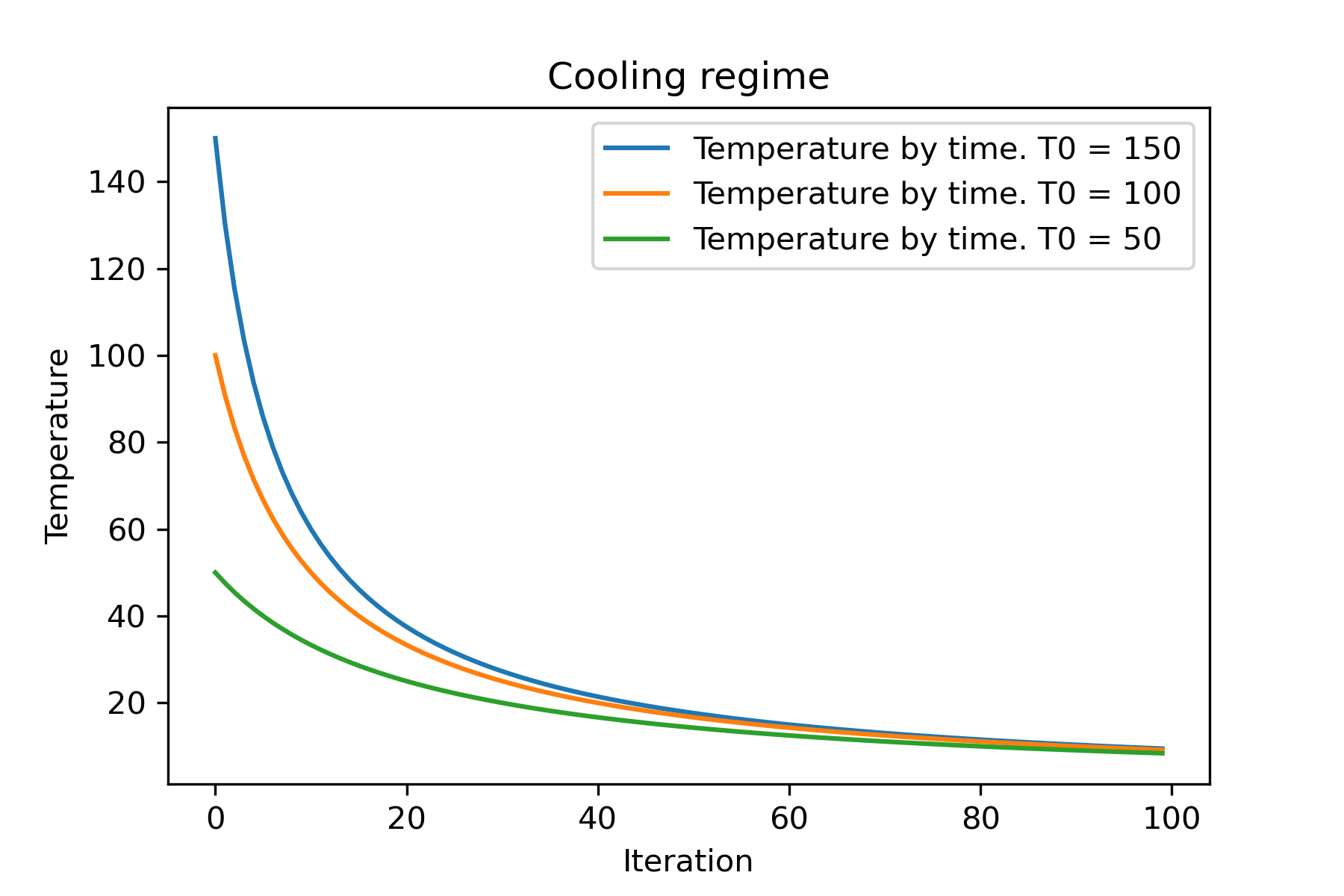
# or several coolings (for each dimention)
temperature = 100
cooling = [
Cooling . reverse ( beta = 0.0001 ),
Cooling . reverse ( beta = 0.0005 ),
Cooling . reverse ( beta = 0.001 )
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'reverse_diff_beta.png' )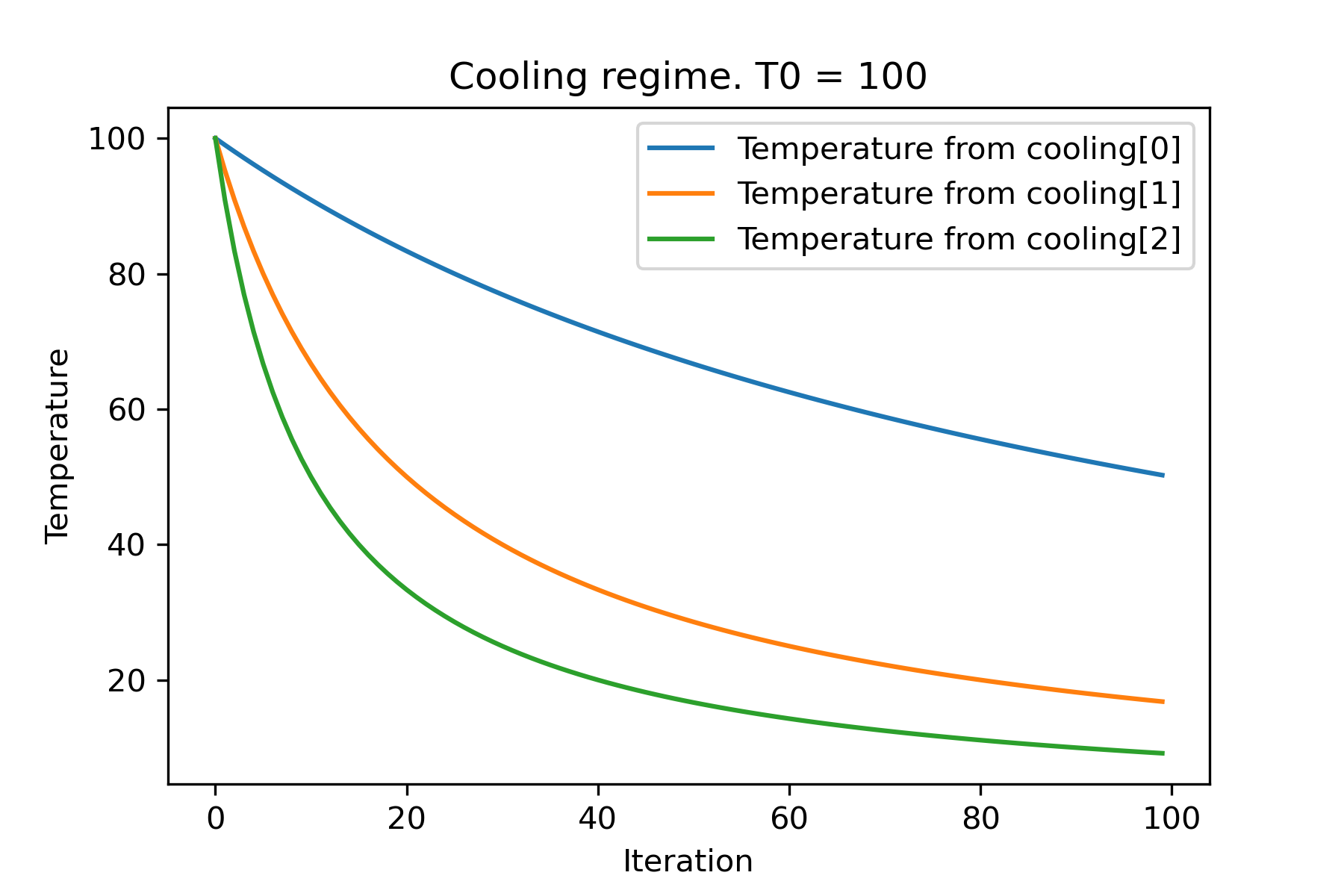
# all supported coolling regimes
temperature = 100
cooling = [
Cooling . linear ( mu = 1 ),
Cooling . reverse ( beta = 0.0007 ),
Cooling . exponential ( alpha = 0.85 ),
Cooling . linear_reverse (),
Cooling . logarithmic ( c = 100 , d = 1 )
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'diff_temp.png' )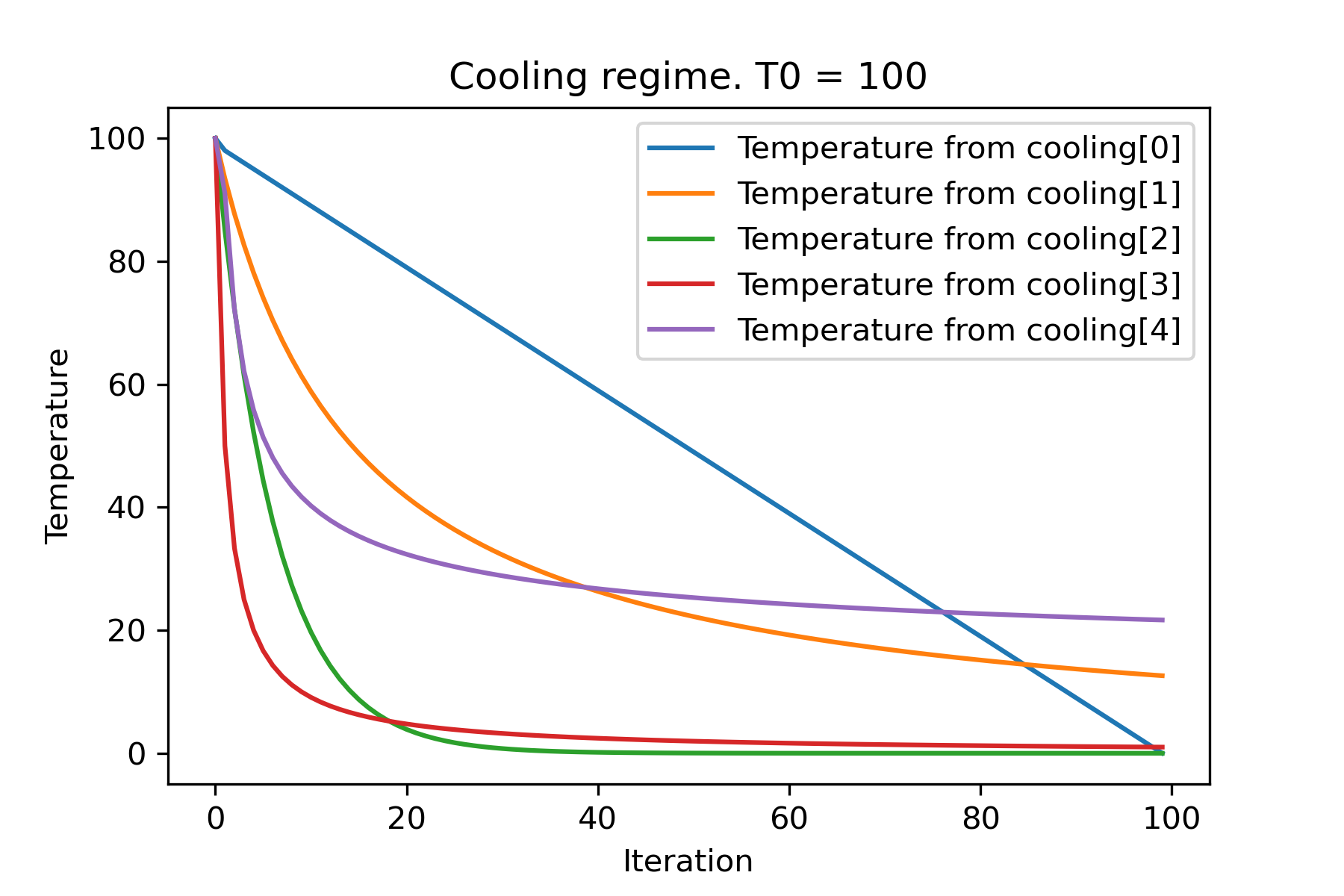
# and we can set own temperature and cooling for each dimention!
temperature = [ 100 , 125 , 150 ]
cooling = [
Cooling . exponential ( alpha = 0.85 ),
Cooling . exponential ( alpha = 0.9 ),
Cooling . exponential ( alpha = 0.95 ),
]
SimulatedAnnealing . plot_temperature ( cooling , temperature , iterations = 100 , save_as = 'diff_temp_and_cool.png' )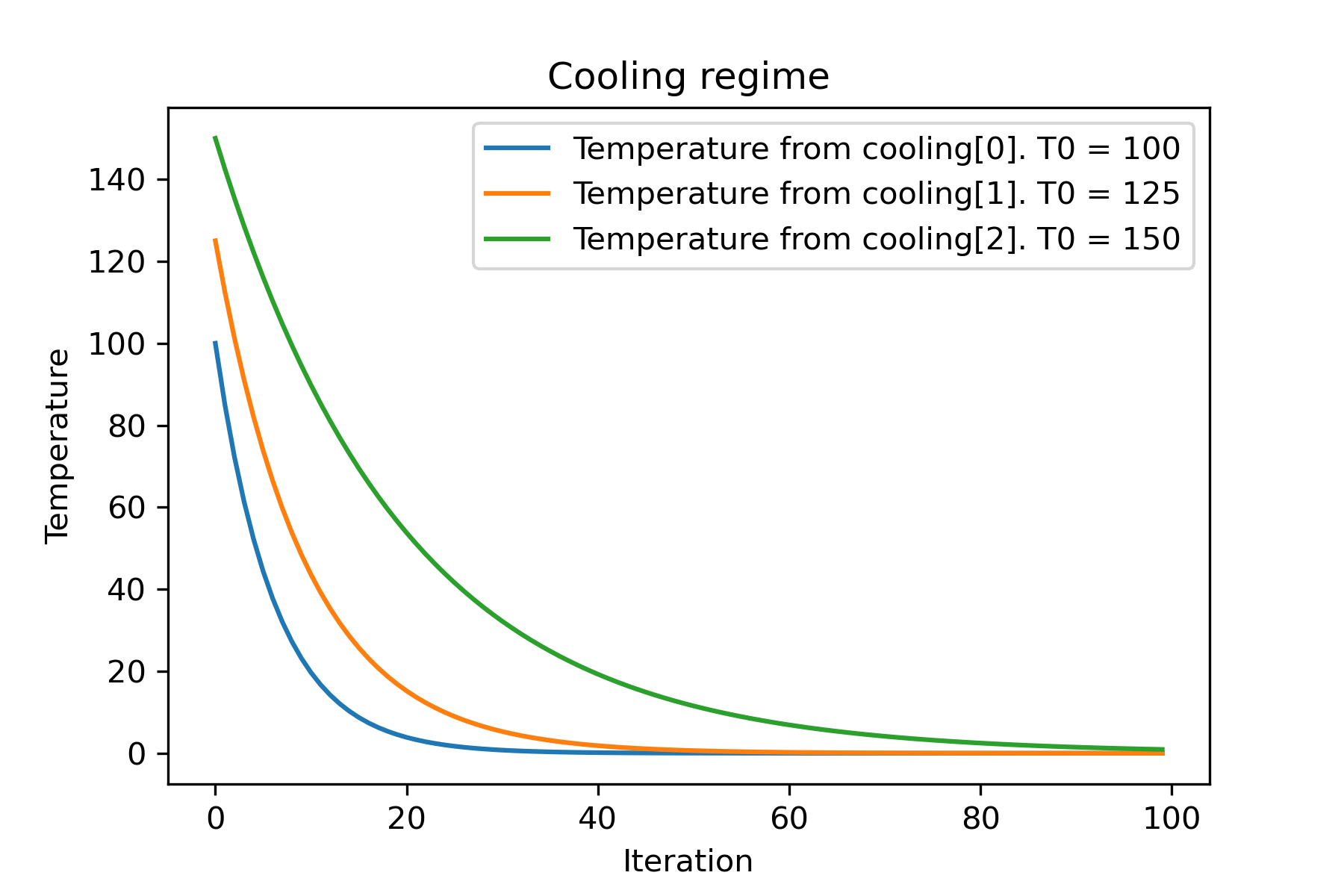
Pourquoi il y a tant de régimes de refroidissement? Pour une certaine tâche, l'un d'eux peut être si meilleur! Dans ce script, nous pouvons tester différents refroidissement pour la fonction RASTRING:
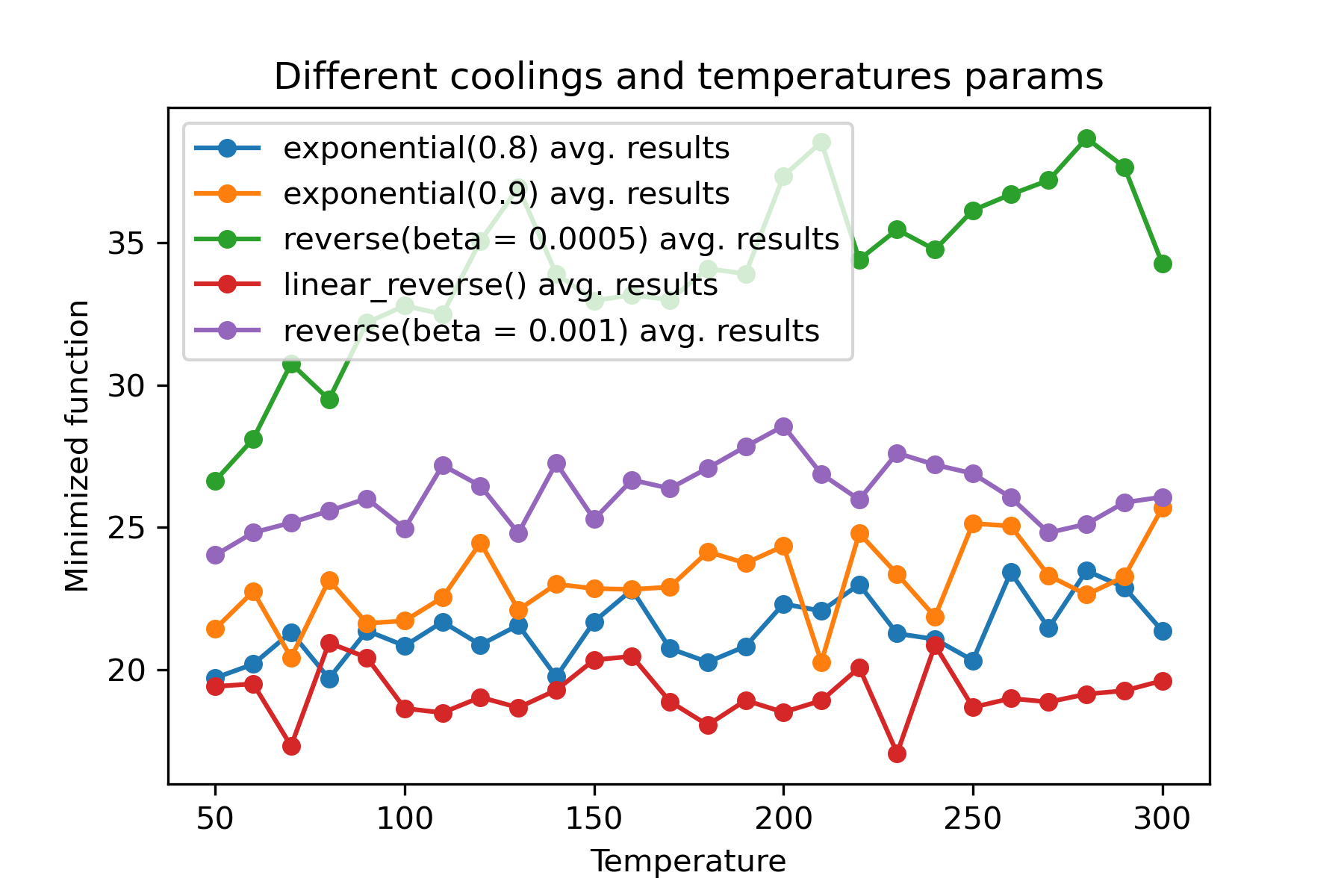
C'est une fonctionnalité incroyable pour utiliser différents refroidissement et démarrer des températures pour chaque dimension :
import math
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling , simple_continual_mutation
def Rastrigin ( arr ):
return 10 * arr . size + np . sum ( arr ** 2 ) - 10 * np . sum ( np . cos ( 2 * math . pi * arr ))
dim = 5
model = SimulatedAnnealing ( Rastrigin , dim )
best_solution , best_val = model . run (
start_solution = np . random . uniform ( - 5 , 5 , dim ),
mutation = simple_continual_mutation ( std = 1 ),
cooling = [ # different cooling for each dimention
Cooling . exponential ( 0.8 ),
Cooling . exponential ( 0.9 ),
Cooling . reverse ( beta = 0.0005 ),
Cooling . linear_reverse (),
Cooling . reverse ( beta = 0.001 )
],
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 250 ,
step_for_reinit_temperature = 90 ,
reinit_from_best = False
)
print ( best_val )
model . plot_report ( save_as = 'different_coolings.png' )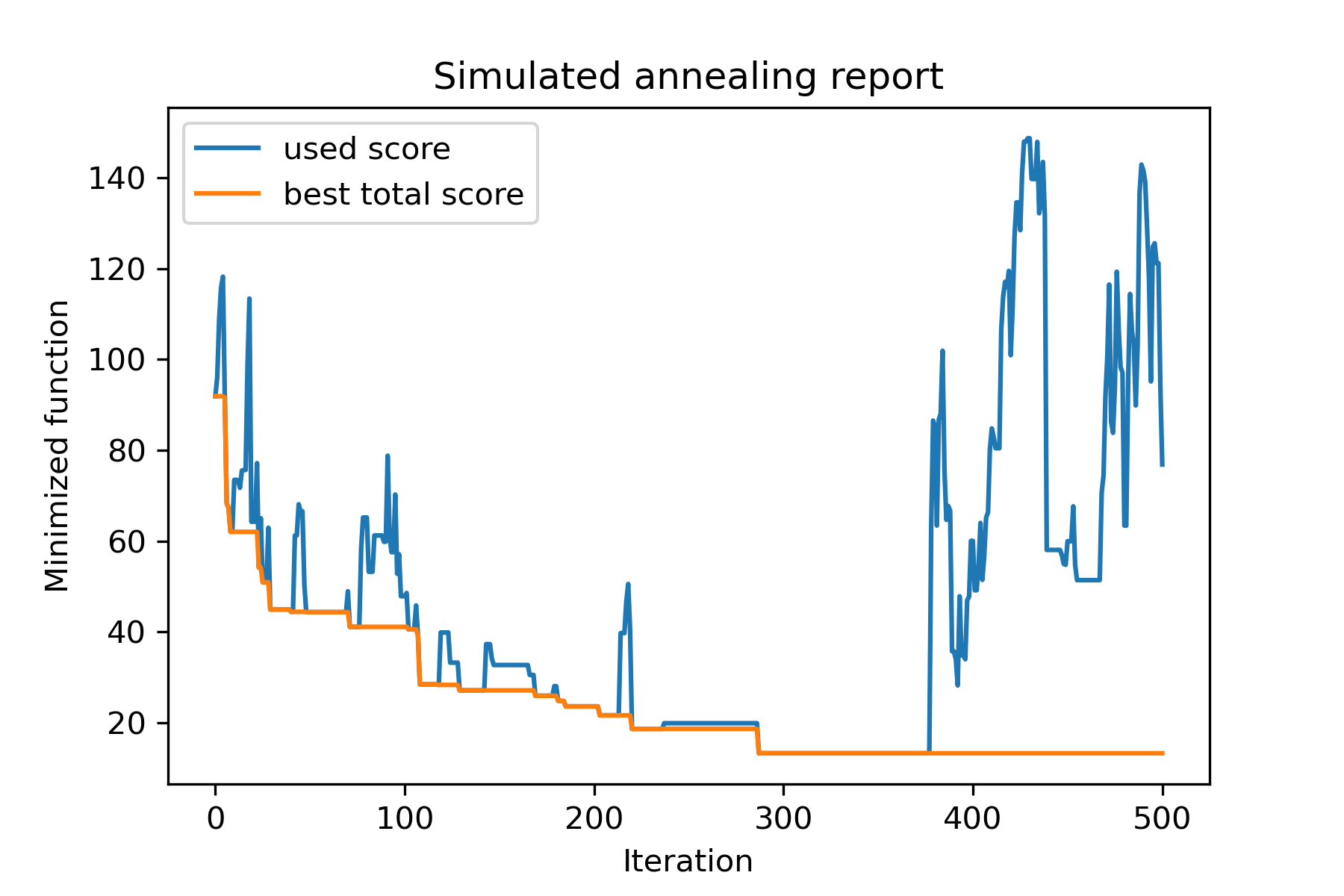
La raison principale d'utiliser plusieurs refroidissement est le comportement de spécification de chaque dimension. Par exemple, la première dimension de l'espace peut être beaucoup plus large que la deuxième dimension, il est donc préférable d'utiliser une recherche plus large pour la première dimension; Vous pouvez le produire en utilisant une fonction mut spéciale, en utilisant différentes start temperatures et en utilisant différents coolings .
Une autre raison d'utiliser plusieurs refroidissement est le moyen de sélection: pour plusieurs refroidissements , la sélection entre les bonnes et les mauvaises solutions s'applique à chaque dimension . Donc, cela augmente les chances de trouver une meilleure solution.
La fonction de mutation est le paramètre le plus important. Il détermine le comportement de la création de nouveaux objets en utilisant des informations sur l'objet actuel et sur la température. Je recommande de compter ces principes lors de la création de la fonction mut :
Rappelons la structure de mut :
def mut ( x_as_array , temperature_as_array_or_one_number ):
# some code
return new_x_as_array Ici x_as_array est la solution actuelle et new_x_as_array est la solution mutée (aléatoire et avec le même dim, ce qui vous en souvenait). Vous devez également vous rappeler que temperature_as_array_or_one_number est le numéro uniquement pour la solution de non-solution. Sinon (lors de l'utilisation de plusieurs températures de démarrage de plusieurs refroidissements ou les deux), c'est un réseau Numpy . Voir des exemples
Dans cet exemple, je montre comment sélectionner les objets k à partir de définir avec n objets qui minimiseront une fonction (dans cet exemple: valeur absolue de la médiane):
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
SEED = 3
np . random . seed ( SEED )
Set = np . random . uniform ( low = - 15 , high = 5 , size = 100 ) # all set
dim = 10 # how many objects should we choose
indexes = np . arange ( Set . size )
# minimized function -- subset with best |median|
def min_func ( arr ):
return abs ( np . median ( Set [ indexes [ arr . astype ( bool )]]))
# zero vectors with 'dim' ones at random positions
start_solution = np . zeros ( Set . size )
start_solution [ np . random . choice ( indexes , dim , replace = False )] = 1
# mutation function
# temperature is the number cuz we will use only 1 cooling, but it's not necessary to use it)
def mut ( x_as_array , temperature_as_array_or_one_number ):
mask_one = x_as_array == 1
mask_zero = np . logical_not ( mask_one )
new_x_as_array = x_as_array . copy ()
# replace some zeros with ones
new_x_as_array [ np . random . choice ( indexes [ mask_one ], 1 , replace = False )] = 0
new_x_as_array [ np . random . choice ( indexes [ mask_zero ], 1 , replace = False )] = 1
return new_x_as_array
# creating a model
model = SimulatedAnnealing ( min_func , dim )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80 ,
seed = SEED
)
model . plot_report ( save_as = 'best_subset.png' )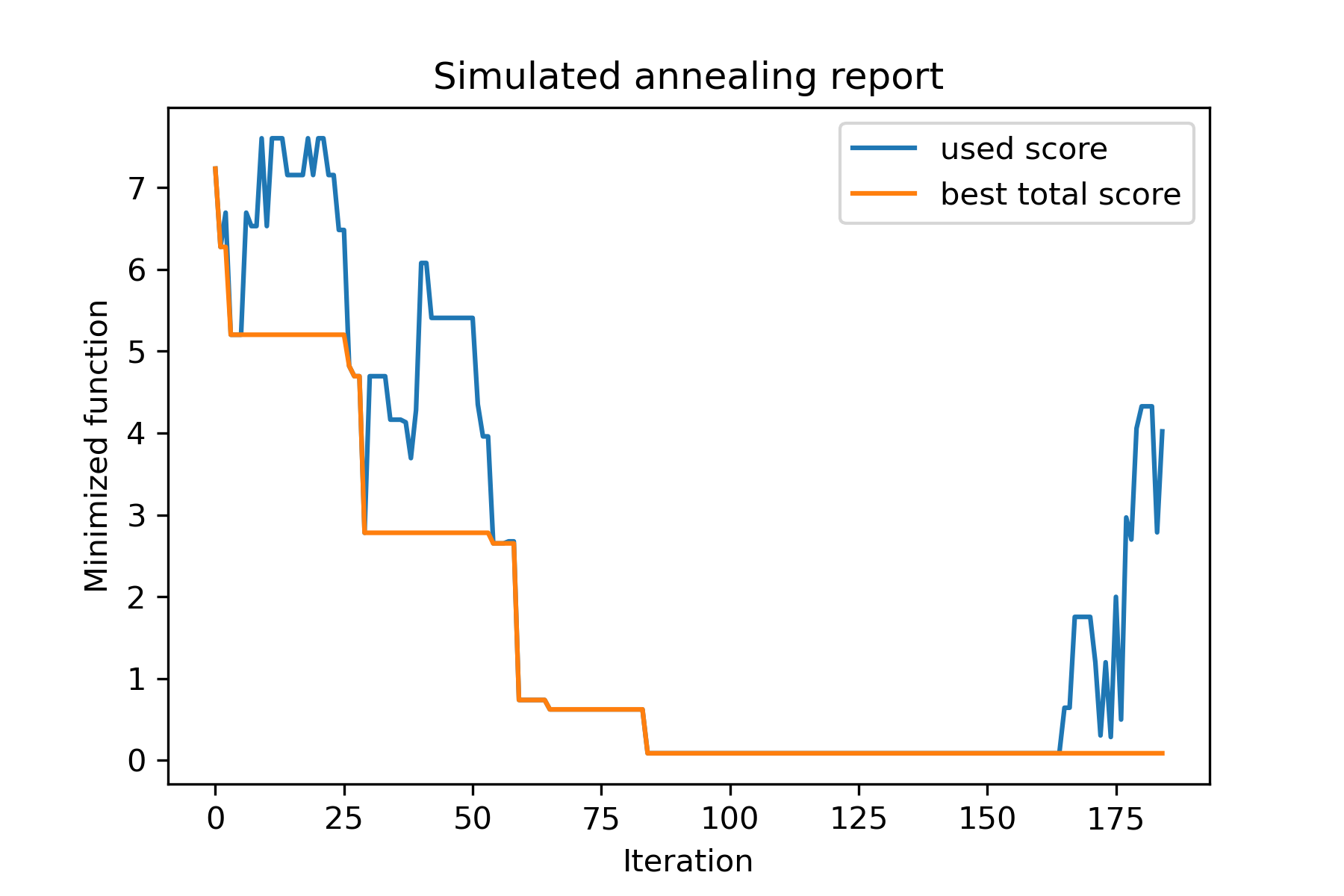
Jetons un coup d'œil à cette tâche:
split set of values {v1, v2, v3, ..., vn} to sets 0, 1, 2, 3
with their sizes (volumes determined by user) to complete best sets metric
Une des façons de le résoudre:
from collections import defaultdict
import numpy as np
from SimplestSimulatedAnnleaning import SimulatedAnnealing , Cooling
################### useful methods
def counts_to_vec ( dic_count ):
"""
converts dictionary like {1: 3, 2: 4}
to array [1, 1, 1, 2, 2, 2, 2]
"""
arrs = [ np . full ( val , fill_value = key ) for key , val in dic_count . items ()]
return np . concatenate ( tuple ( arrs ))
def vec_to_indexes_dict ( vector ):
"""
converts vector like [1, 0, 1, 2, 2]
to dictionary with indexes {1: [0, 2], 2: [3, 4]}
"""
res = defaultdict ( list )
for i , v in enumerate ( vector ):
res [ v ]. append ( i )
return { int ( key ): np . array ( val ) for key , val in res . items () if key != 0 }
#################### START PARAMS
SEED = 3
np . random . seed ( SEED )
Set = np . random . uniform ( low = - 15 , high = 5 , size = 100 ) # all set
Set_indexes = np . arange ( Set . size )
# how many objects should be in each set
dim_dict = {
1 : 10 ,
2 : 10 ,
3 : 7 ,
4 : 14
}
# minimized function: sum of means vy each split set
def min_func ( arr ):
indexes_dict = vec_to_indexes_dict ( arr )
means = [ np . mean ( Set [ val ]) for val in indexes_dict . values ()]
return sum ( means )
# zero vector with available set labels at random positions
start_solution = np . zeros ( Set . size , dtype = np . int8 )
labels_vec = counts_to_vec ( dim_dict )
start_solution [ np . random . choice ( Set_indexes , labels_vec . size , replace = False )] = labels_vec
def choice ( count = 3 ):
return np . random . choice ( Set_indexes , count , replace = False )
# mutation function
# temperature is the number cuz we will use only 1 cooling, but it's not necessary to use it)
def mut ( x_as_array , temperature_as_array_or_one_number ):
new_x_as_array = x_as_array . copy ()
# replace some values
while True :
inds = choice ()
if np . unique ( new_x_as_array [ inds ]). size == 1 : # there is no sense to replace same values
continue
new_x_as_array [ inds ] = new_x_as_array [ np . random . permutation ( inds )]
return new_x_as_array
# creating a model
model = SimulatedAnnealing ( min_func , Set_indexes . size )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 1000 ,
max_iterations_without_progress = 100 ,
step_for_reinit_temperature = 80 ,
seed = SEED ,
reinit_from_best = True
)
model . plot_report ( save_as = 'best_split.png' )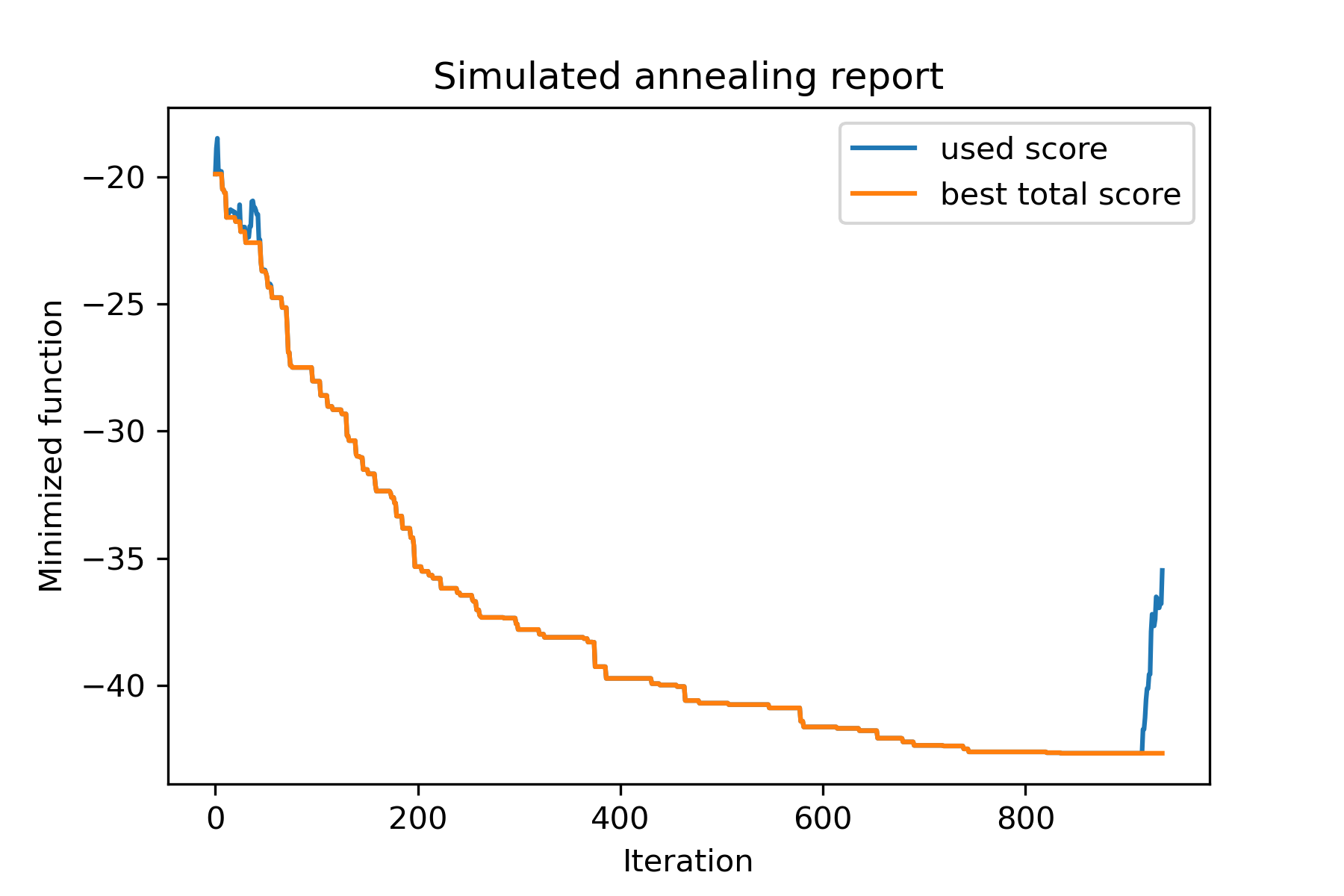
Essayons de résoudre le problème des vendeurs itinérants pour la tâche Berlin52. Dans cette tâche, il y a 52 villes avec des coordonnées du fichier.
Tout d'abord, importons des packages:
import math
import numpy as np
import pandas as pd
import matplotlib . pyplot as plt
from SimplestSimulatedAnnleaning import SimulatedAnnealing , CoolingRéglez les graines pour la reproduction:
SEED = 1
np . random . seed ( SEED )Lire les coordonnées et créer une matrice de distance:
# read coordinates
coords = pd . read_csv ( 'berlin52_coords.txt' , sep = ' ' , header = None , names = [ 'index' , 'x' , 'y' ])
# dim is equal to count of cities
dim = coords . shape [ 0 ]
# distance matrix
distances = np . empty (( dim , dim ))
for i in range ( dim ):
distances [ i , i ] = 0
for j in range ( i + 1 , dim ):
d = math . sqrt ( np . sum (( coords . iloc [ i , 1 :] - coords . iloc [ j , 1 :]) ** 2 ))
distances [ i , j ] = d
distances [ j , i ] = dCréer une solution de démarrage aléatoire:
indexes = np . arange ( dim )
# some start solution (indexes shuffle)
start_solution = np . random . choice ( indexes , dim , replace = False )Définissez une fonction qui calcule la longueur:
# minized function
def way_length ( arr ):
s = 0
for i in range ( 1 , dim ):
s += distances [ arr [ i - 1 ], arr [ i ]]
# also we should end the way in the beggining
s += distances [ arr [ - 1 ], arr [ 1 ]]
return sVisualisez la solution de démarrage:
def plotData ( indices , title , save_as = None ):
# create a list of the corresponding city locations:
locs = [ coords . iloc [ i , 1 :] for i in indices ]
locs . append ( coords . iloc [ indices [ 0 ], 1 :])
# plot a line between each pair of consequtive cities:
plt . plot ( * zip ( * locs ), linestyle = '-' , color = 'blue' )
# plot the dots representing the cities:
plt . scatter ( coords . iloc [:, 1 ], coords . iloc [:, 2 ], marker = 'o' , s = 40 , color = 'red' )
plt . title ( title )
if not ( save_as is None ): plt . savefig ( save_as , dpi = 300 )
plt . show ()
# let's plot start solution
plotData ( start_solution , f'start random solution (score = { round ( way_length ( start_solution ), 2 ) } )' , 'salesman_start.png' )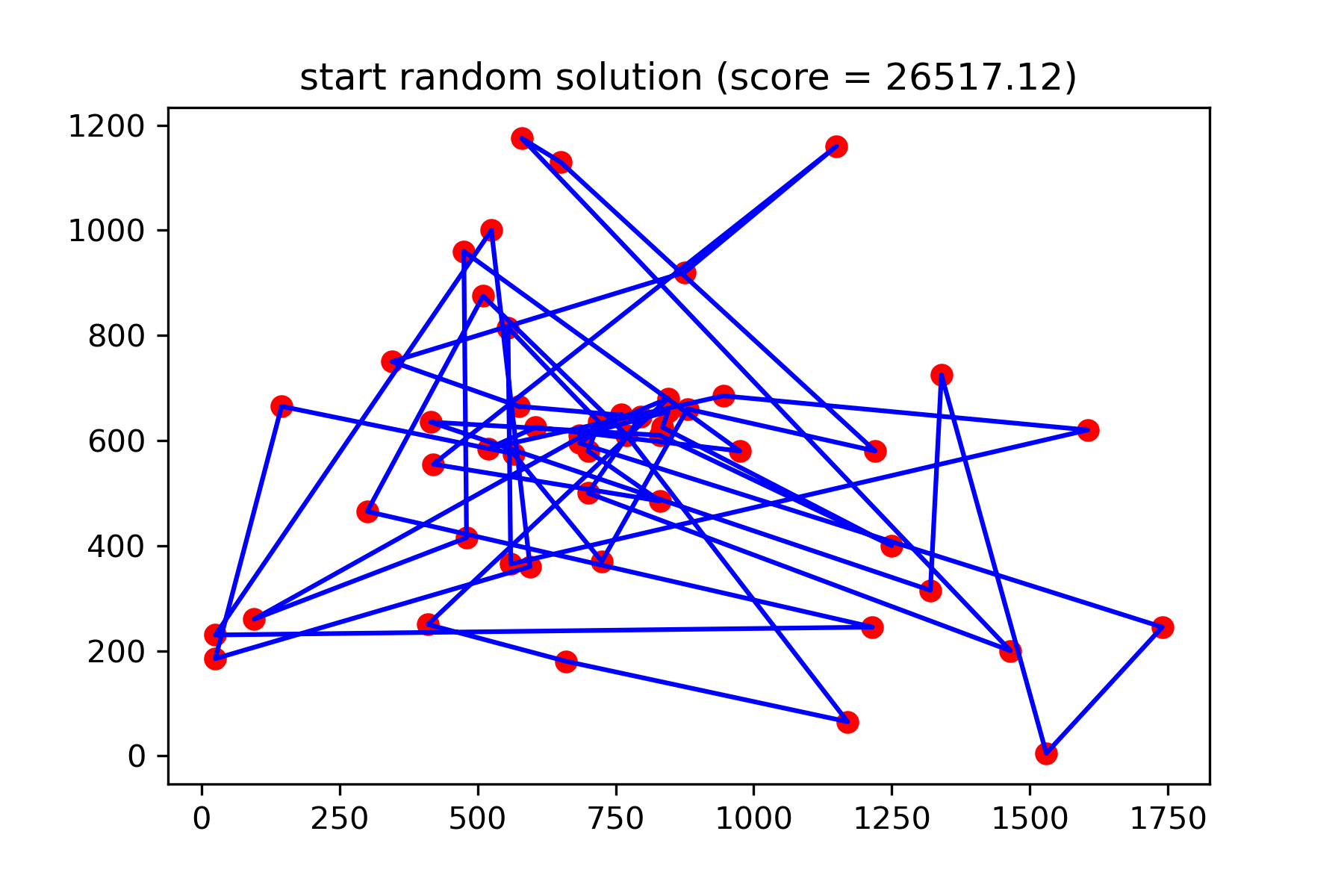
Ce n'est vraiment pas une bonne solution. Je veux créer cette fonction de mutation pour cette tâche:
def mut ( x_as_array , temperature_as_array_or_one_number ):
# random indexes
rand_inds = np . random . choice ( indexes , 3 , replace = False )
# shuffled indexes
goes_to = np . random . permutation ( rand_inds )
# just replace some positions in the array
new_x_as_array = x_as_array . copy ()
new_x_as_array [ rand_inds ] = new_x_as_array [ goes_to ]
return new_x_as_arrayCommencez à rechercher:
# creating a model
model = SimulatedAnnealing ( way_length , dim )
# run search
best_solution , best_val = model . run (
start_solution = start_solution ,
mutation = mut ,
cooling = Cooling . exponential ( 0.9 ),
start_temperature = 100 ,
max_function_evals = 15000 ,
max_iterations_without_progress = 2000 ,
step_for_reinit_temperature = 80 ,
reinit_from_best = True ,
seed = SEED
)
model . plot_report ( save_as = 'best_salesman.png' )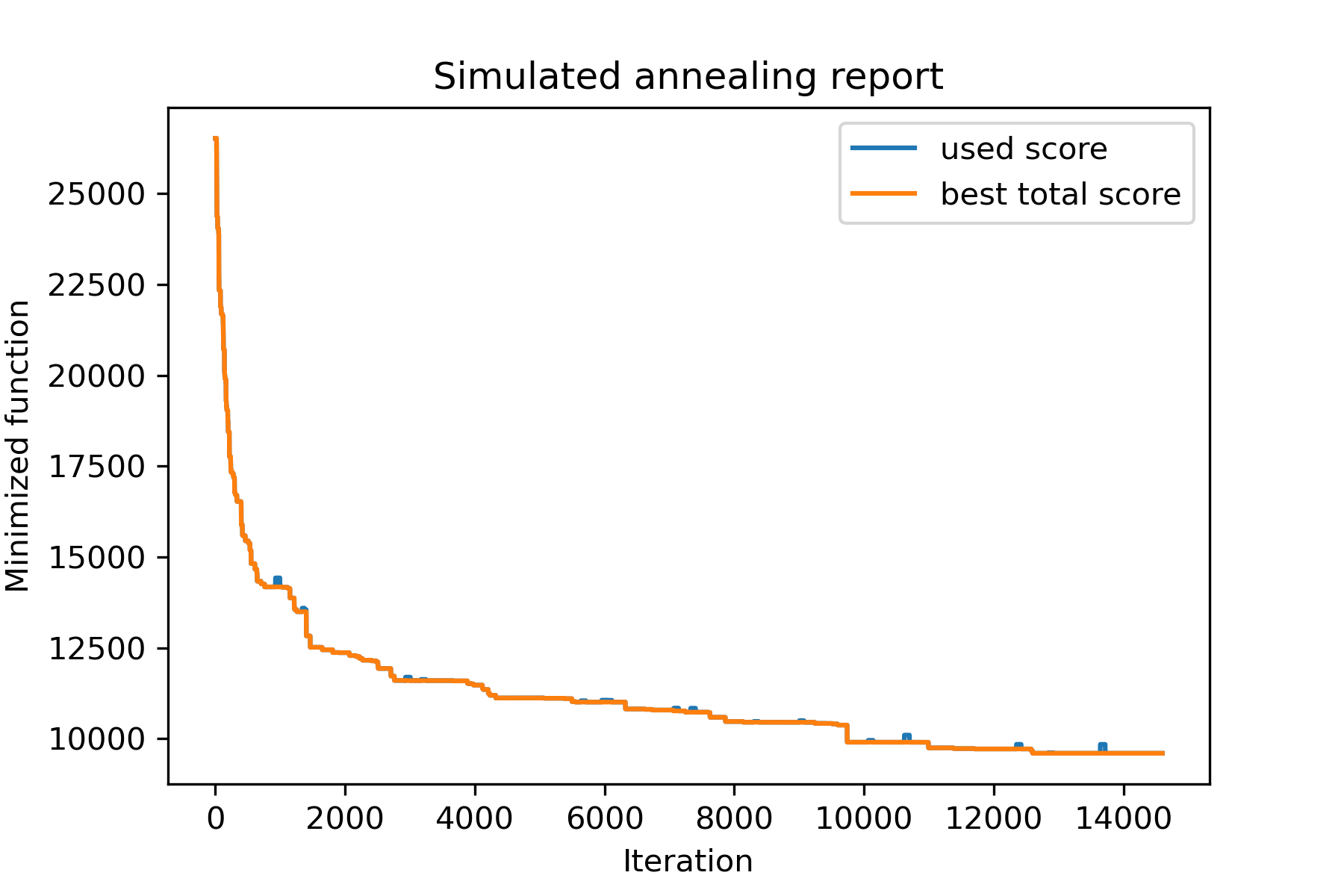
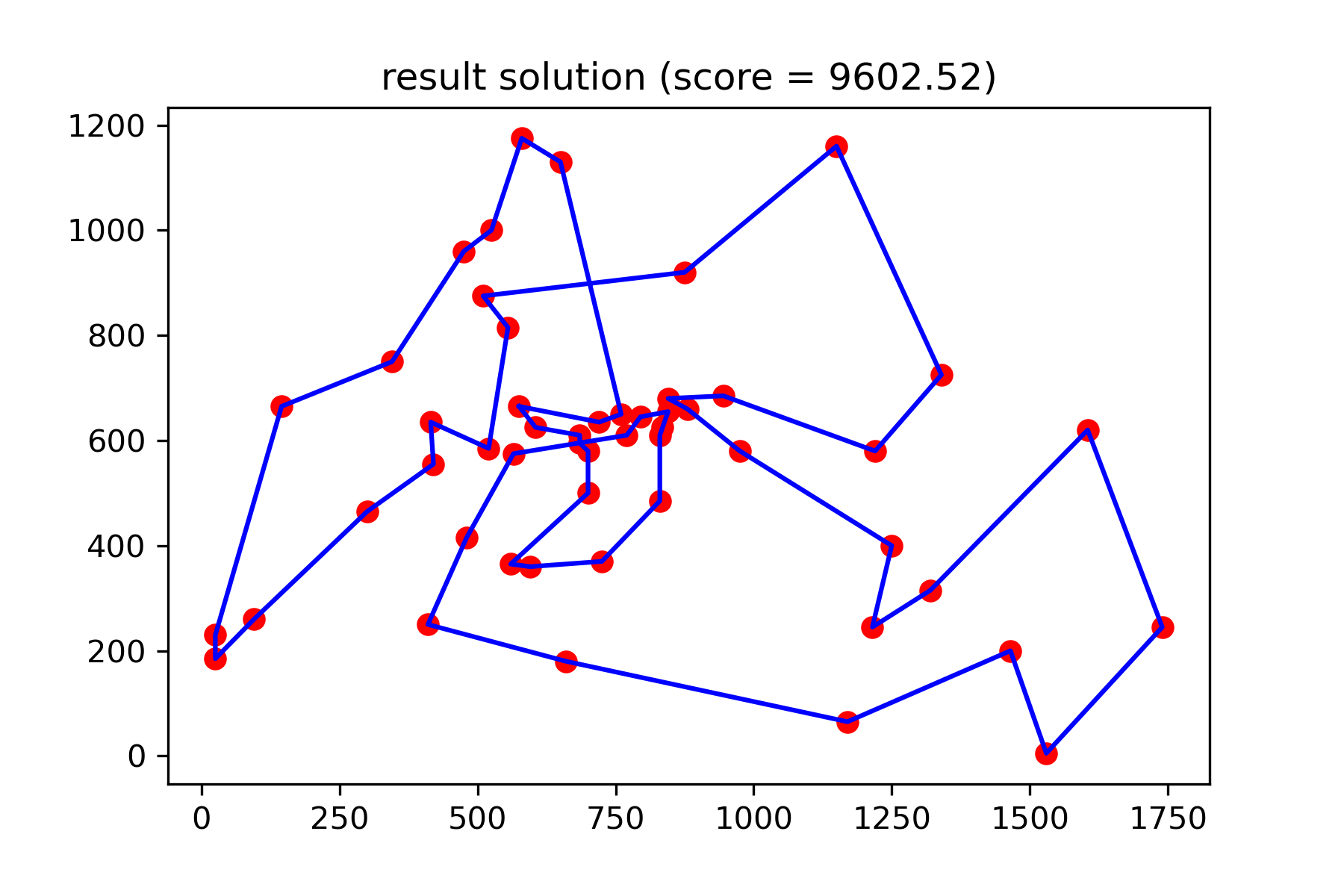
Et voir notre solution tellement meilleure:
plotData ( best_solution , f'result solution (score = { round ( best_val , 2 ) } )' , 'salesman_result.png' )