Реализация реляционных повторных нейронных сетей DeepMind (Santoro et al. 2018) в Pytorch.
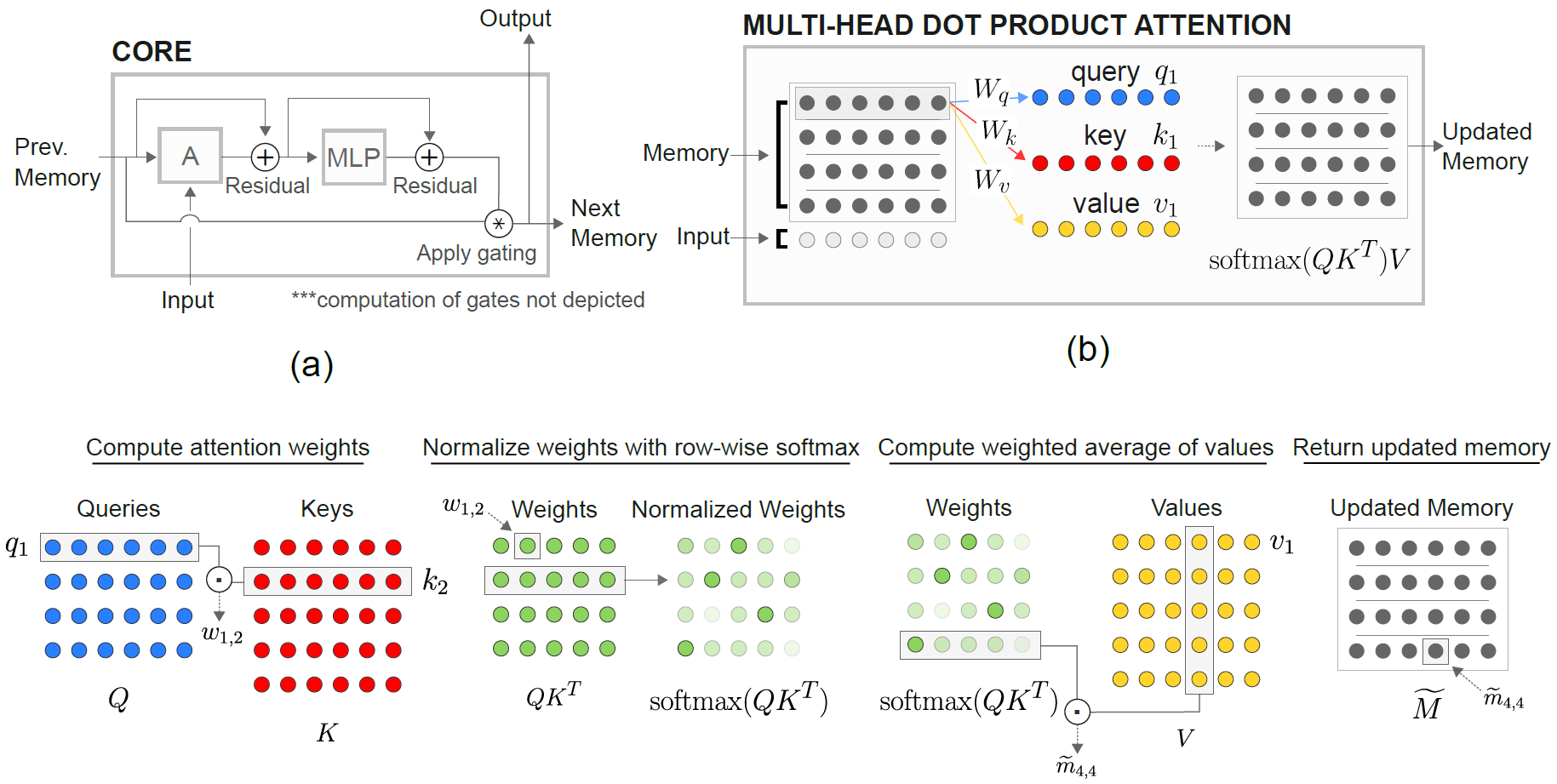
Модуль реляционной памяти (RMC) первоначально от официальной реализации сонета. Тем не менее, в настоящее время они не предоставляют контрольный код с полным языком.
Это репо является портом RMC с дополнительными комментариями. Он имеет полноценный эталон моделирования языка слов против традиционного LSTM.
Он поддерживает любой произвольный текстовый набор данных на основе токенов, включая Wikitext-2 и Wikitext-103.
Обе модели RMC и LSTM поддерживают адаптивный SoftMax для гораздо более низкого использования памяти большого набора данных словарного запаса. RMC поддерживает DataParallel Pytorch, так что вы можете легко экспериментировать с настройкой с несколькими GPU.
Контрольные коды жестко подготовлены от официального примера на языке словесного языка Pytorch
Он также оснащен N-тревой дальнейшей синтетической задачей из бумаги (см. Ниже).
Pytorch 0,4,1 или более поздней версии (протестирован на 1,0,0) и Python 3.6
python train_rmc.py --cuda для полного обучения и тестового прогона RMC с графическим процессором.
python train_rmc.py --cuda --adaptivesoftmax --cutoffs 1000 5000 20000 Если использование большого набора данных словаря (например, Wikitext-103), чтобы соответствовать всем тензорам в VRAM.
python generate_rmc.py --cuda для генерации предложений из обученной модели.
python train_rnn.py --cuda для полного обучения и тестового прогона традиционного RNN с графическим процессором.
Все гиперпараметры по умолчанию RMC & LSTM являются результатами двухнедельного эксперимента с использованием Wikitext-2.
Протестировано с помощью Wikitext-2 и Wikitext-103. Wikitext-2 в комплекте.
Создайте подпапку внутри ./data и поместите train.txt , valid.txt и test.txt в подпапке.
Укажите --data=(subfolder name) , и вы готовы идти.
Код выполняет токенизацию при первом обучении, а корпус сохраняется как pickle . Код загрузит файл pickle после первого запуска.
Оба RMC и LSTM имеют параметры ~ 11 м. Пожалуйста, обратитесь к коду обучения для получения подробной информации о гиперпараметрах.
| Модели | Действительное недоумение | Тест недоумения | Передний проход MS/PACTION (Titan XP) | Передний проход MS/PACTION (Titan V) |
|---|---|---|---|---|
| LSTM (cudnn) | 111.31 | 105,56 | 26 ~ 27 | 40 ~ 41 |
| LSTM (для петли) | То же, что и Cudnn | То же, что и Cudnn | 30 ~ 31 | 60 ~ 61 |
| RMC | 112,77 | 107.21 | 110 ~ 130 | 220 ~ 230 |
RMC может достичь сопоставимой производительности с LSTM (с поиском тяжелых гиперпараметрических), но оказывается, что RMC очень медленный. Мульти-головное самопринятие на каждом временном шаге может быть виновником здесь. Использование LSTMCell с For Loop (который является более «справедливым» эталоном для RMC) замедляет передний проход, но он все равно намного быстрее.
Пожалуйста, также обратите внимание, что гиперпараметр для RMC является наихудшим сценарием с точки зрения скорости, потому что он использовал один слот памяти (как описано в статье) и не выиграл от распределения веса в ряду из памяти с несколькими слотами.
Интересно отметить, что скорость медленнее в Titan V, чем Titan XP. Причина может заключаться в том, что модели относительно небольшие, и модель часто вызывает небольшие линейные операции.
Возможно, Titan XP (~ 1900 МГц разблокировал тактовую скорость CUDA против лимита Titan V 1335 МГц) получает выгоду от такой рабочей нагрузки. Или, может быть, задержка запуска Cuda Cuda Cuda выше для OPS в модели.
Я не эксперт в деталях CUDA. Пожалуйста, поделитесь своими результатами!
Параметры внимания, как правило, переполняют Wikitext-2. Уменьшение гиперпармет для внимания (key_size) может бороться с переосмыслением.
Применение отсева на выходном логите до того, как SoftMax (например, LSTM One) помогло предотвратить переживание.
| Встроенный и размер головы | # головы | Внимание слоев MLP | размер ключа | выбросить на выходе | Слоты памяти | тест на пп |
|---|---|---|---|---|---|---|
| 128 | 4 | 3 | 128 | Нет | 1 | 128.81 |
| 128 | 4 | 3 | 128 | Нет | 1 | 128.81 |
| 128 | 8 | 3 | 128 | Нет | 1 | 141.84 |
| 128 | 4 | 3 | 32 | Нет | 1 | 123,26 |
| 128 | 4 | 3 | 32 | Да | 1 | 112.4 |
| 128 | 4 | 3 | 64 | Нет | 1 | 124,44 |
| 128 | 4 | 3 | 64 | Да | 1 | 110.16 |
| 128 | 4 | 2 | 64 | Да | 1 | 111.67 |
| 64 | 4 | 3 | 64 | Да | 1 | 133,68 |
| 64 | 4 | 3 | 32 | Да | 1 | 135,93 |
| 64 | 4 | 3 | 64 | Да | 4 | 137.93 |
| 192 | 4 | 3 | 64 | Да | 1 | 107.21 |
| 192 | 4 | 3 | 64 | Да | 4 | 114,85 |
| 256 | 4 | 3 | 256 | Нет | 1 | 194.73 |
| 256 | 4 | 3 | 64 | Да | 1 | 126.39 |
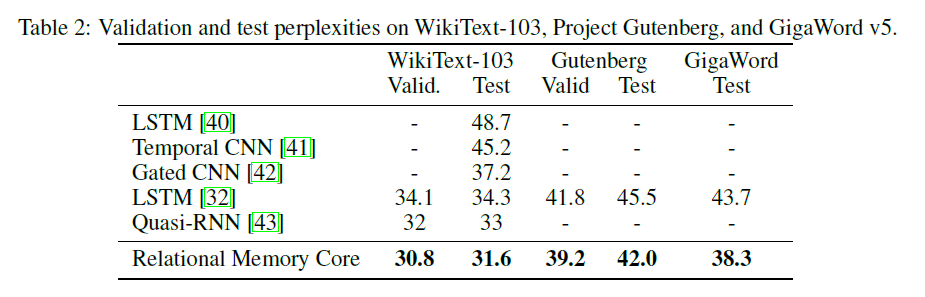
Оригинальная бумага RMC представляет результаты Wikitext-103 с большим размером модели и партии (6 Tesla P100, каждый с размером 64 партии, так что в общей сложности 384. Ой).
Использование полного Softmax легко взрывает VRAM. Использование --adaptivesoftmax настоятельно рекомендуется. При использовании --adaptivesoftmax , --cutoffs должны быть должным образом предоставлены. Пожалуйста, обратитесь к оригинальному описанию API
У меня нет такого оборудования, и мой ресурс слишком ограничен, чтобы провести эксперименты. Учебный результат, или любой другой вклад очень приветствуются!
Цель задания состоит в том, чтобы: k, случайно помеченная (от 1 до K) D-димерных векторов, определить, какой из них является самым дальним вектором от вектора М. (Ответ является целым числом от 1 до к.)
Конкретная задача в статье: дано 8 помеченных 16-мерных векторов, которые являются самым дальним вектором от вектора M? Векторы помечены случайным образом, поэтому модель должна признать, что вектор Mth является вектором, помеченным как M, в отличие от вектора в положении Mth на входе.
Вход в модель состоит из 8 40-мерных векторов для каждого примера. Каждый из этих 40-мерных векторов структурирован как это:
[(vector 1) (label: which vector is it, from 1 to 8, one-hot encoded) (N, one-hot encoded) (M, one-hot encoded)]
python train_nth_farthest.py --cuda для обучения и тестирования по самой дальней задаче с графическим процессором (ы).
Это использует класс RelationalMemory в relational_rnn_general.py , который является версией relational_rnn_models.py без специфического кода моделирования языка.
Пожалуйста, обратитесь к train_nth_farthest.py для получения подробной информации о значениях гиперпараметра. Они взяты из Приложения A1 в статье и в реализации сонета, когда значения гиперпараметра не указаны в статье.
Примечание. Новые примеры генерируются на эпоху, как в реализации сонета. Похоже, что это согласуется с статьей, в которой не указано количество используемых примеров.
Модель была обучена одним графическим процессором Titan XP навсегда, пока не достигнет 91% точности теста. Ниже приведены результаты с 3 независимыми прогонами: 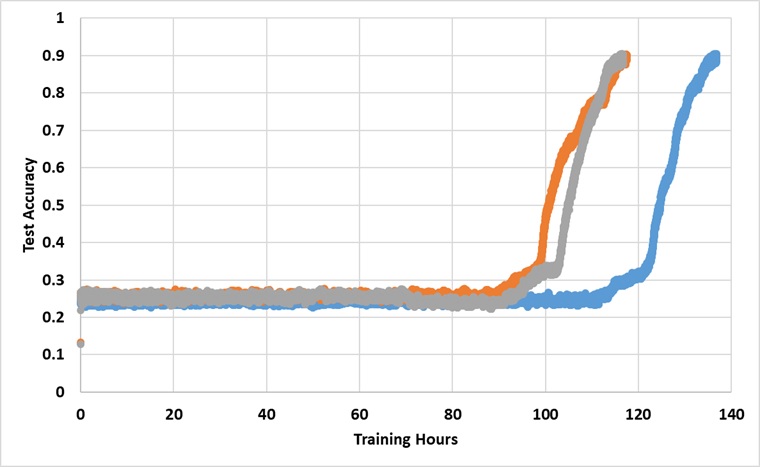
Модель действительно преодолевает барьер 25%, если она обучена достаточно долго, но время настенных часов примерно в 2 ~ 3 раза больше, чем сообщалось в бумаге.
Экспериментируйте с различными гиперпараметрами