Eine Implementierung von DeepMinds relationalen wiederkehrenden neuronalen Netzwerken (Santoro et al. 2018) in Pytorch.
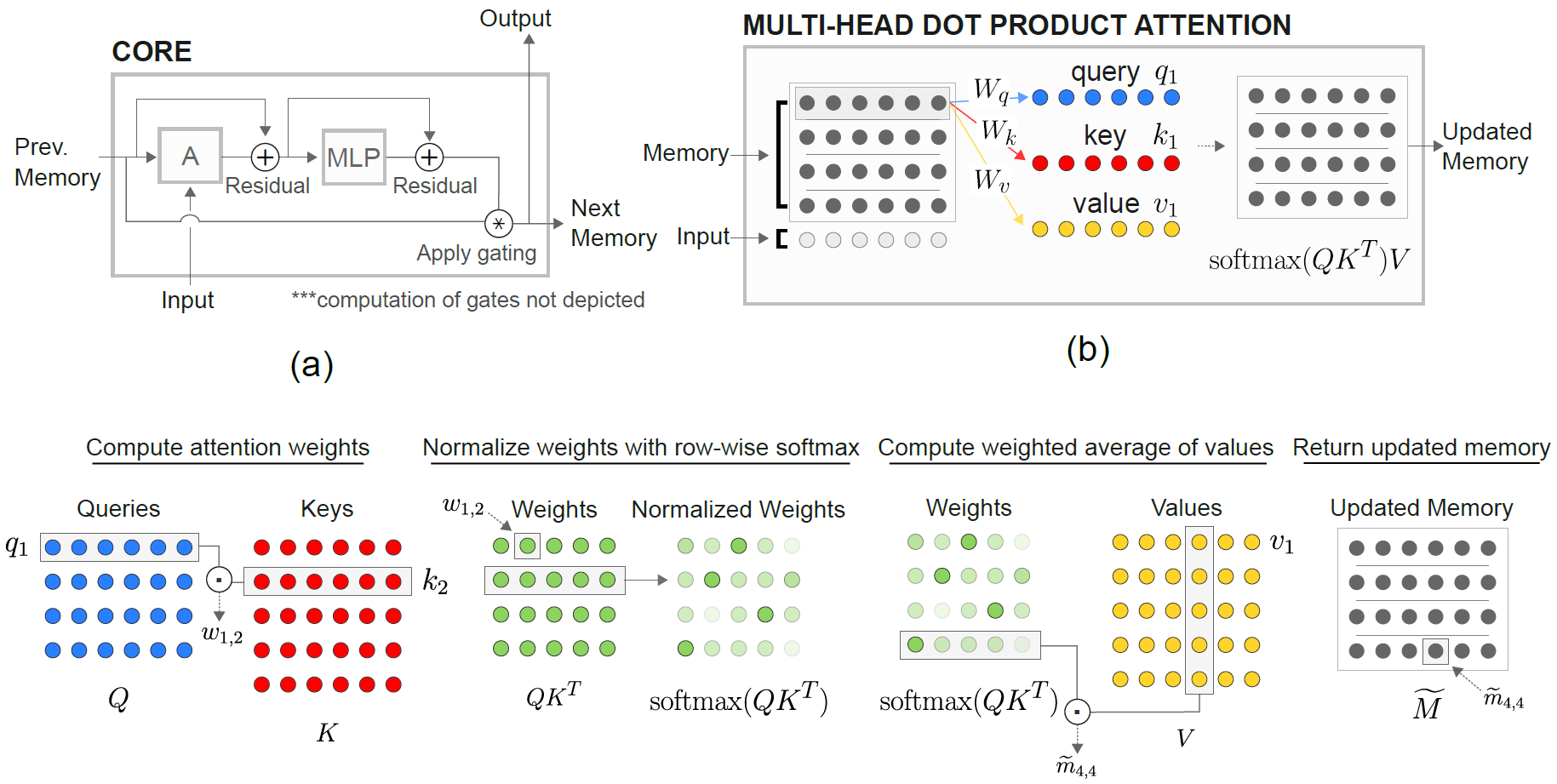
Das RMC -Modul (Relational Memory Core) stammt ursprünglich aus der offiziellen Sonnet -Implementierung. Derzeit bieten sie jedoch keinen umfassenden Benchmark -Code für Sprachmodellierung.
Dieses Repo ist ein Port von RMC mit zusätzlichen Kommentaren. Es verfügt über ein vollwertiges Wortmodellierungsbenchmark im Vergleich zu traditioneller LSTM.
Es unterstützt alle beliebigen Text-Token-basierten Textdatensatz, einschließlich Wikitext-2 & Wikitext-103.
Sowohl RMC- als auch LSTM -Modelle unterstützen adaptive Softmax für eine viel geringere Verwendung von großem Vokabular -Datensatz. RMC unterstützt Pytorchs DataParallel , sodass Sie problemlos mit einem Multi-GPU-Setup experimentieren können.
Benchmark-Codes sind hartnäckig vom offiziellen Beispiel für Pytorch-Word-Sprache-Modell
Es verfügt auch über eine n-tedste synthetische Aufgabe aus dem Papier (siehe unten).
Pytorch 0.4.1 oder höher (getestet auf 1.0.0) & Python 3.6
python train_rmc.py --cuda für vollständige Trainings- und Testlauf von RMC mit GPU.
python train_rmc.py --cuda --adaptivesoftmax --cutoffs 1000 5000 20000 Wenn Sie einen großen Vokabular-Datensatz (wie Wikitext-103) verwenden, um alle Tensoren in das VRAM anzupassen.
python generate_rmc.py --cuda zum Generieren von Sätzen aus dem trainierten Modell.
python train_rnn.py --cuda für vollständige Trainings- und Testlauf von traditionellem RNN mit GPU.
Alle Standardhyperparameter von RMC und LSTM sind Ergebnisse eines zweiwöchigen Experiments mit Wikitext-2.
Getestet mit Wikitext-2 und Wikitext-103. Wikitext-2 ist gebündelt.
Erstellen Sie einen Unterordner im Inneren ./data und platzieren Sie Word-Level train.txt , valid.txt und test.txt im Unterordner.
Geben Sie --data=(subfolder name) an und Sie können loslegen.
Der Code führt beim ersten Trainingslauf eine Tokenisierung durch, und der Korpus wird als pickle gespeichert. Der Code lädt die pickle nach dem ersten Lauf.
Sowohl RMC als auch LSTM haben ~ 11m -Parameter. Weitere Informationen zu Hyperparametern finden Sie im Trainingscode.
| Modelle | Gültige Verwirrung | Verwirrung testen | Vorwärtspass MS/Batch (Titan XP) | Vorwärtspass MS/Batch (Titan V) |
|---|---|---|---|---|
| LSTM (CUDNN) | 111.31 | 105,56 | 26 ~ 27 | 40 ~ 41 |
| LSTM (für Schleife) | Gleich wie Cudnn | Gleich wie Cudnn | 30 ~ 31 | 60 ~ 61 |
| RMC | 112.77 | 107.21 | 110 ~ 130 | 220 ~ 230 |
RMC kann eine vergleichbare Leistung mit LSTM erreichen (mit schwerer Hyperparameter -Suche), aber es stellt sich heraus, dass der RMC sehr langsam ist. Die Selbstbeziehung mit mehreren Kopf zu jedem Zeitschritt kann hier der Schuldige sein. Die Verwendung von LSTMCell mit für Loop (was "fairer" Benchmark für RMC ist) verlangsamt den Vorwärtspass, aber es ist immer noch viel schneller.
Bitte beachten Sie außerdem, dass der Hyperparameter für RMC in Bezug auf die Geschwindigkeit ein Worst-Case-Szenario ist, da er einen einzelnen Speicherplatz verwendet hat (wie im Papier beschrieben) und nicht von einer zeilenweise Gewichtsaustausch aus dem Multi-Slot-Speicher profitiert.
Interessant zu beachten, dass die Geschwindigkeit in Titan V langsamer ist als Titan XP. Der Grund könnte sein, dass die Modelle relativ klein sind und das Modell häufig kleine lineare Operationen aufruft.
Vielleicht profitiert Titan XP (~ 1.900 MHz freigeschaltete Cuda Clock -Geschwindigkeit gegenüber Titan Vs 1.335 MHz Limit) von dieser Art der Arbeitsbelastung. Oder vielleicht ist der Cuda -Kernel -Startlatenz von Titan V für die OPS im Modell höher.
Ich bin kein Experte in Details von CUDA. Bitte teilen Sie Ihre Ergebnisse!
Aufmerksamkeitsparameter neigen dazu, das Wikitext-2 zu überwinden. Durch die Reduzierung der Hyperparmeter für die Aufmerksamkeit (key_size) kann die Überanpassung bekämpfen.
Das Anwenden des Ausfalls auf den Ausgangslogit vor dem Softmax (wie der LSTM One) half dies, die Überanpassung zu verhindern.
| Einbettung und Kopfgröße | # Köpfe | Achtung MLP -Schichten | Schlüsselgröße | Ausfall bei Ausgang | Speicherplätze | ppl |
|---|---|---|---|---|---|---|
| 128 | 4 | 3 | 128 | NEIN | 1 | 128.81 |
| 128 | 4 | 3 | 128 | NEIN | 1 | 128.81 |
| 128 | 8 | 3 | 128 | NEIN | 1 | 141.84 |
| 128 | 4 | 3 | 32 | NEIN | 1 | 123.26 |
| 128 | 4 | 3 | 32 | Ja | 1 | 112.4 |
| 128 | 4 | 3 | 64 | NEIN | 1 | 124.44 |
| 128 | 4 | 3 | 64 | Ja | 1 | 110.16 |
| 128 | 4 | 2 | 64 | Ja | 1 | 111.67 |
| 64 | 4 | 3 | 64 | Ja | 1 | 133.68 |
| 64 | 4 | 3 | 32 | Ja | 1 | 135.93 |
| 64 | 4 | 3 | 64 | Ja | 4 | 137.93 |
| 192 | 4 | 3 | 64 | Ja | 1 | 107.21 |
| 192 | 4 | 3 | 64 | Ja | 4 | 114.85 |
| 256 | 4 | 3 | 256 | NEIN | 1 | 194.73 |
| 256 | 4 | 3 | 64 | Ja | 1 | 126.39 |
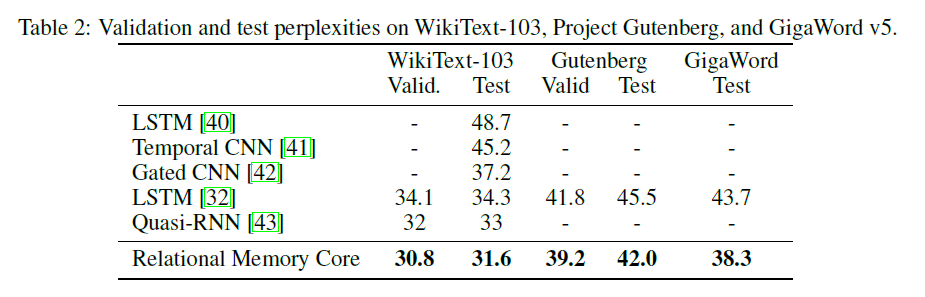
Das ursprüngliche RMC-Papier enthält Wikitext-103-Ergebnisse mit einer größeren Modell- und Stapelgröße (6 Tesla P100 mit jeweils 64 Chargengröße, also insgesamt 384. Autsch).
Mit einem vollständigen Softmax wird das VRAM leicht aufblasen. Die Verwendung --adaptivesoftmax wird sehr empfohlen. Wenn Sie --adaptivesoftmax verwenden, sollten ordnungsgemäß --cutoffs bereitgestellt werden. Bitte beachten Sie die ursprüngliche API -Beschreibung
Ich habe keine solche Hardware und meine Ressource ist zu beschränkt, um die Experimente durchzuführen. Benchmark -Ergebnis oder andere Beiträge sind sehr willkommen!
Das Ziel der Aufgabe ist: Wenn k zufällig gekennzeichnet ist (von 1 bis k) d-dimensionale Vektoren, identifizieren Sie, welches der n-te weiteste Vektor von Vector M ist (die Antwort ist eine Ganzzahl von 1 bis k.)
Die spezifische Aufgabe in der Arbeit lautet: gegeben 8 mit 16-dimensionale Vektoren gekennzeichnete Vektoren, was der am weitesten entfernte Vektor von Vektor m ist? Die Vektoren sind zufällig markiert, sodass das Modell erkennen muss, dass der mth -Vektor der als M bezeichnete Vektor im Gegensatz zum Vektor in der mth -Position in der Eingabe ist.
Die Eingabe zum Modell umfasst für jedes Beispiel 8 40-dimensionale Vektoren. Jedes dieser 40-dimensionalen Vektoren ist so strukturiert:
[(vector 1) (label: which vector is it, from 1 to 8, one-hot encoded) (N, one-hot encoded) (M, one-hot encoded)]
python train_nth_farthest.py --cuda für das Training und Testen über die am weitesten entfernte Aufgabe mit GPU (s).
Dies verwendet die RelationalMemory Klasse in relational_rnn_general.py , einer Version von relational_rnn_models.py ohne den sprachlich modellierten Code.
Weitere Informationen zu Hyperparameterwerten finden Sie unter train_nth_farthest.py . Diese stammen aus Anhang A1 im Papier und aus der Sonnet -Implementierung, wenn die Hyperparameterwerte in der Arbeit nicht angegeben sind.
Hinweis: Pro Epoche werden neue Beispiele wie in der Sonnet -Implementierung generiert. Dies scheint mit dem Papier übereinzustimmen, das nicht die Anzahl der verwendeten Beispiele angibt.
Das Modell wurde für immer mit einer einzelnen Titan XP -GPU trainiert, bis es 91% Testgenauigkeit erreicht. Im Folgenden finden Sie die Ergebnisse mit 3 unabhängigen Läufen: 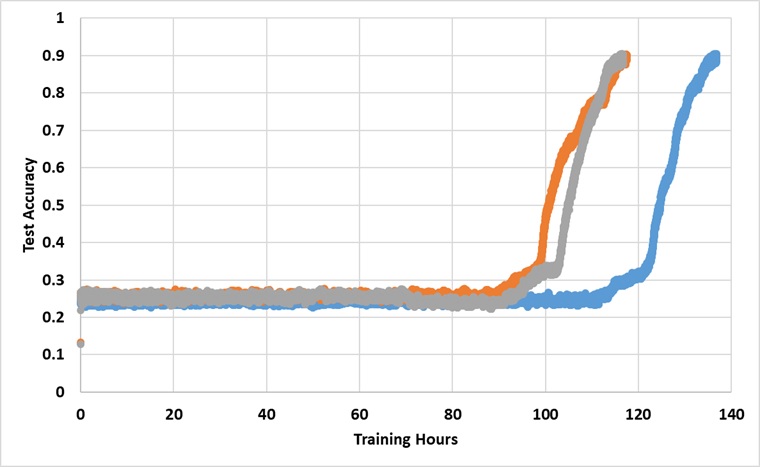
Das Modell bricht die 25% Barriere, wenn sie lange genug trainiert wird, aber die Wanduhrzeit ist ungefähr 2 ~ 3x länger als die in der Zeitung angegeben.
Experimentieren Sie mit verschiedenen Hyperparametern