Uma implementação das redes neurais recorrentes relacionais do DeepMind (Santoro et al. 2018) em Pytorch.
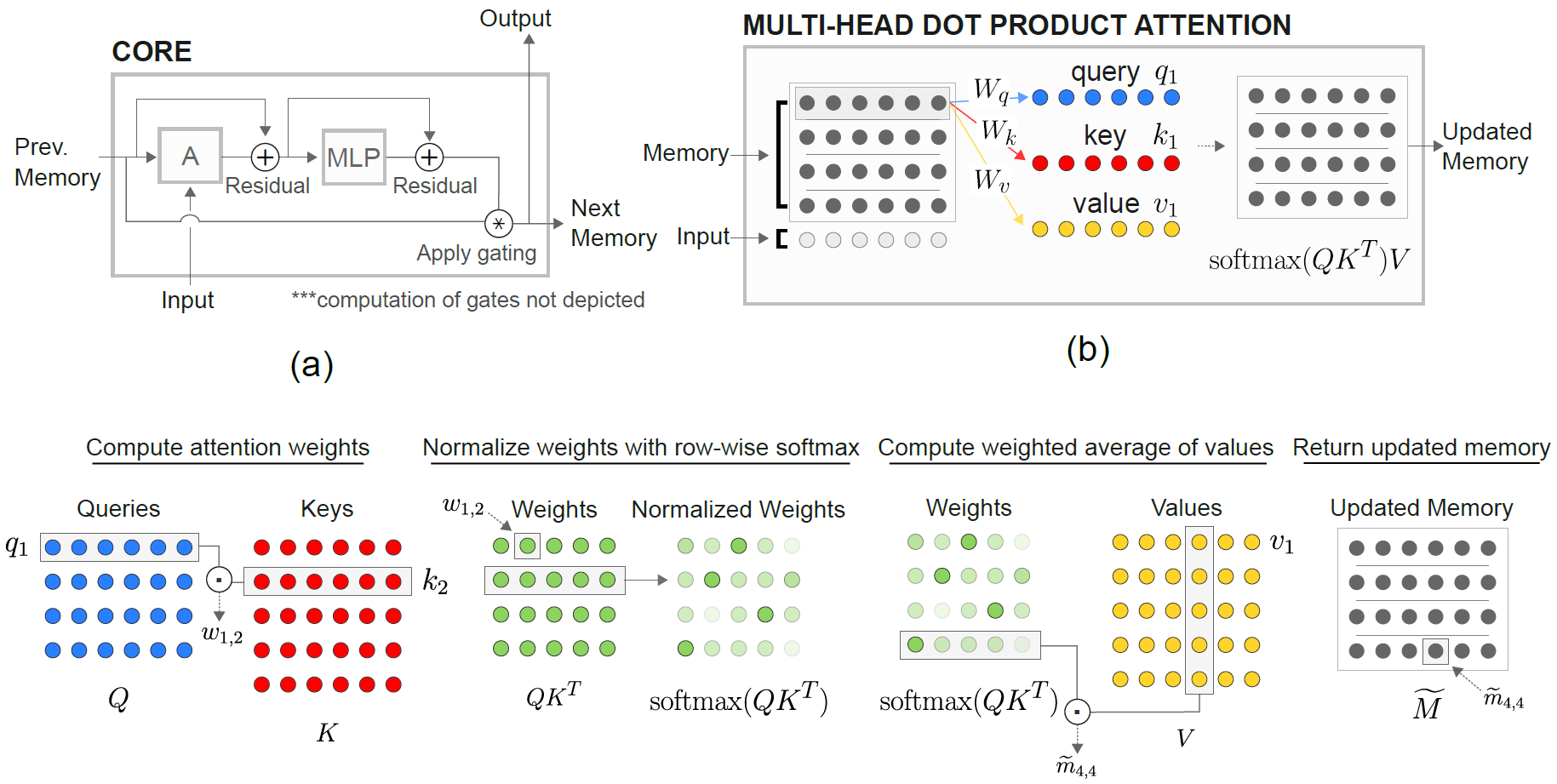
O módulo Core de Memória Relacional (RMC) é originalmente da implementação oficial do SONNET. No entanto, atualmente eles não fornecem um código de benchmark de modelagem de idiomas completo.
Este repositório é um porto de RMC com comentários adicionais. Possui um benchmark de modelagem de linguagem de palavras completos vs. LSTM tradicional.
Ele suporta qualquer conjunto de dados de texto arbitrário baseado em token, incluindo Wikitext-2 e Wikitext-103.
Os modelos RMC e LSTM suportam o Softmax adaptativo para o uso de memória muito mais baixo do conjunto de dados de vocabulário grande. O RMC suporta DataParallel de Pytorch, para que você possa experimentar facilmente uma configuração multi-GPU.
Os códigos de referência são forçados a partir do exemplo oficial de Pytorch Word-Language-Model
Ele também possui uma tarefa sintética mais distante do artigo (veja abaixo).
Pytorch 0.4.1 ou posterior (testado em 1.0.0) e Python 3.6
python train_rmc.py --cuda para treinamento completo e teste de RMC com GPU.
python train_rmc.py --cuda --adaptivesoftmax --cutoffs 1000 5000 20000 Se estiver usando um conjunto de dados de vocabulário grande (como o Wikitext-103) para atender a todos os tensores do VRAM.
python generate_rmc.py --cuda para gerar frases a partir do modelo treinado.
python train_rnn.py --cuda para treinamento completo e teste de RNN tradicional com GPU.
Todos os hiperparâmetros padrão do RMC e LSTM são resultados de um experimento de duas semanas usando o Wikitext-2.
Testado com Wikitext-2 e Wikitext-103. Wikitext-2 é incluído.
Crie uma subpasta dentro ./data e coloque train.txt de nível de palavra.txt, valid.txt e test.txt dentro da subpasta.
Especifique --data=(subfolder name) e você está pronto para ir.
O código executa tokenização na primeira execução de treinamento e o corpus é salvo como pickle . O código carregará o arquivo pickle após a primeira execução.
Ambos RMC e LSTM têm ~ 11m parâmetros. Consulte o código de treinamento para obter detalhes sobre hiperparameters.
| Modelos | Perplexidade válida | Teste perplexidade | Pass Ms/Lote (Titan XP) | Pass MS/Batch (Titan V) |
|---|---|---|---|---|
| LSTM (CUDNN) | 111.31 | 105.56 | 26 ~ 27 | 40 ~ 41 |
| LSTM (para loop) | O mesmo que Cudnn | O mesmo que Cudnn | 30 ~ 31 | 60 ~ 61 |
| Rmc | 112.77 | 107.21 | 110 ~ 130 | 220 ~ 230 |
O RMC pode atingir um desempenho comparável ao LSTM (com pesquisa de hiperparâmetro pesada), mas acontece que o RMC é muito lento. A auto-atendimento de várias cabeças a cada passo pode ser o culpado aqui. O uso do LSTMCell com o loop (que é mais "justo" para RMC) diminui o passe para a frente, mas ainda é muito mais rápido.
Observe também que o hiperparâmetro para o RMC é um cenário de pior caso em termos de velocidade, porque usou um único slot de memória (conforme descrito no papel) e não se beneficiou de um compartilhamento de peso em linha com memória de vários slot.
Interessante notar aqui é que a velocidade é mais lenta no Titan V do que o Titan XP. O motivo pode ser que os modelos sejam relativamente pequenos e o modelo chama pequenas operações lineares com frequência.
Talvez o Titan XP (~ 1.900MHz desbloqueou a velocidade do relógio CUDA vs. o limite de 1.335MHz de Titan V) beneficiários desse tipo de carga de trabalho. Ou talvez a latência de lançamento do Kernel CUDA do Titan V seja maior para as OPs no modelo.
Não sou especialista em detalhes de Cuda. Compartilhe seus resultados!
Os parâmetros de atenção tendem a superar o Wikitext-2. Reduzir os hiperparmeters para atenção (key_size) pode combater o excesso de ajuste.
A aplicação do abandono no logit de saída antes do softmax (como o LSTM) ajudou a prevenir o excesso de ajuste.
| Tamanho da incorporação e da cabeça | # cabeças | Atenção Camadas MLP | Tamanho da chave | abandono na saída | slots de memória | teste ppl |
|---|---|---|---|---|---|---|
| 128 | 4 | 3 | 128 | Não | 1 | 128.81 |
| 128 | 4 | 3 | 128 | Não | 1 | 128.81 |
| 128 | 8 | 3 | 128 | Não | 1 | 141.84 |
| 128 | 4 | 3 | 32 | Não | 1 | 123.26 |
| 128 | 4 | 3 | 32 | Sim | 1 | 112.4 |
| 128 | 4 | 3 | 64 | Não | 1 | 124.44 |
| 128 | 4 | 3 | 64 | Sim | 1 | 110.16 |
| 128 | 4 | 2 | 64 | Sim | 1 | 111.67 |
| 64 | 4 | 3 | 64 | Sim | 1 | 133.68 |
| 64 | 4 | 3 | 32 | Sim | 1 | 135.93 |
| 64 | 4 | 3 | 64 | Sim | 4 | 137.93 |
| 192 | 4 | 3 | 64 | Sim | 1 | 107.21 |
| 192 | 4 | 3 | 64 | Sim | 4 | 114.85 |
| 256 | 4 | 3 | 256 | Não | 1 | 194.73 |
| 256 | 4 | 3 | 64 | Sim | 1 | 126.39 |
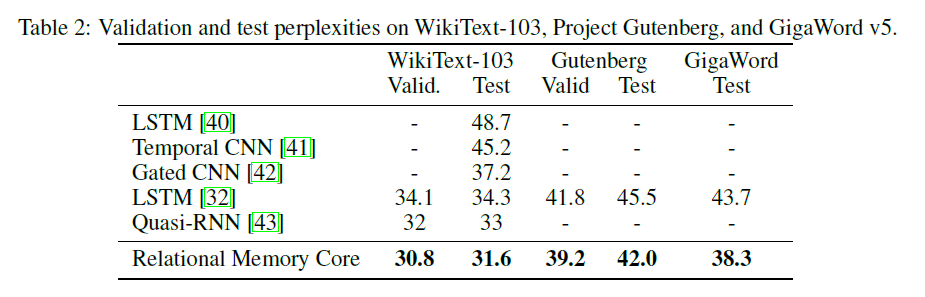
O papel RMC original apresenta o Wikitext-103 resulta com um modelo e tamanho de lote maior (6 Tesla P100, cada um com 64 tamanho em lote, portanto, um total de 384. ai).
O uso de um softmax completo sopra facilmente o VRAM. Usar --adaptivesoftmax é altamente recomendado. Se estiver usando --adaptivesoftmax , --cutoffs deve ser fornecido corretamente. Consulte a descrição da API original
Não tenho esse hardware e meu recurso está muito limitado para fazer os experimentos. Resultado da referência, ou quaisquer outras contribuições são muito bem -vindas!
O objetivo da tarefa é: Dado k rotulado aleatoriamente (de 1 a k) vetores Dimensionais D, identifique qual é o enésimo vetor mais distante do vetor M. (a resposta é um número inteiro de 1 a k.)
A tarefa específica no artigo é: Dado 8 vetores 16-dimensionais, que é o enésimo vetor mais distante do vetor M? Os vetores são rotulados aleatoriamente, de modo que o modelo deve reconhecer que o Mth Vector é o vetor marcado como M, em oposição ao vetor na posição MTH na entrada.
A entrada para o modelo compreende 8 vetores 40-dimensionais para cada exemplo. Cada um desses vetores 40-dimensionais é estruturado assim:
[(vector 1) (label: which vector is it, from 1 to 8, one-hot encoded) (N, one-hot encoded) (M, one-hot encoded)]
python train_nth_farthest.py --cuda para treinamento e teste na enésima tarefa mais distante com as GPU (s).
Isso usa a classe RelationalMemory em relational_rnn_general.py , que é uma versão de relational_rnn_models.py sem o código específico de modelagem de idiomas.
Consulte train_nth_farthest.py para obter detalhes sobre valores de hiperparameter. Eles são retirados do Apêndice A1 no artigo e da implementação do soneto quando os valores do hiperparâmetro não são fornecidos no artigo.
Nota: novos exemplos são gerados por época, como na implementação do soneto. Isso parece ser consistente com o artigo, que não especifica o número de exemplos utilizados.
O modelo foi treinado com uma única GPU do Titan XP para sempre até atingir a precisão de 91% do teste. Abaixo estão os resultados com 3 execuções independentes: 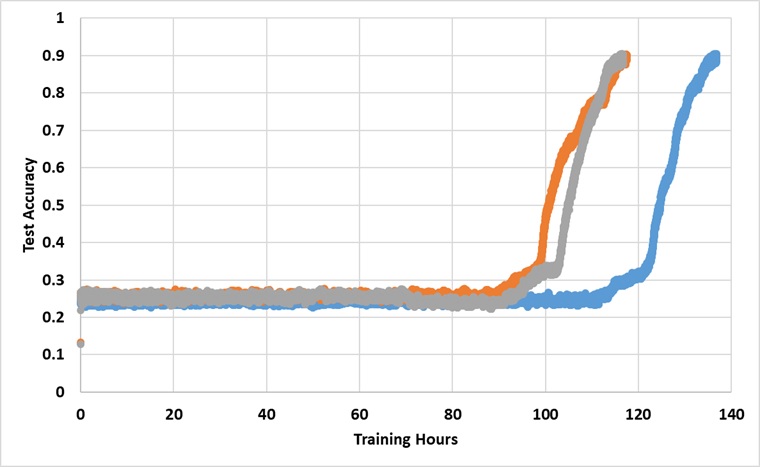
O modelo quebra a barreira de 25% se treinada por tempo suficiente, mas o tempo do relógio da parede é aproximadamente mais de 2 ~ 3x mais do que o relatado no papel.
Experimente com diferentes hiperparâmetros