Una implementación de las redes neuronales recurrentes relacionales de Deepmind (Santoro et al. 2018) en Pytorch.
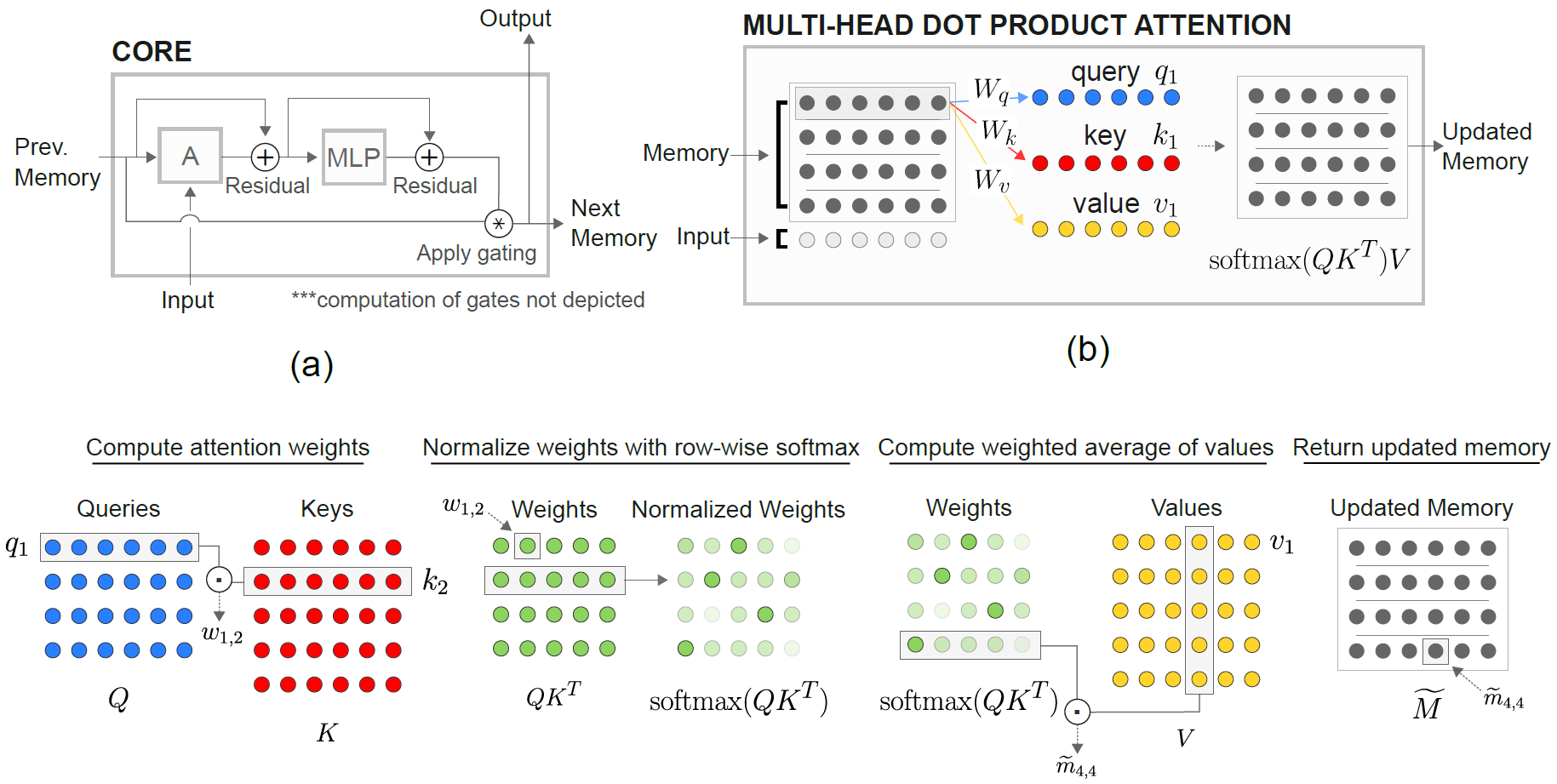
El módulo de núcleo de memoria relacional (RMC) es originaria de la implementación oficial del soneto. Sin embargo, actualmente no proporcionan un código de referencia de modelado de idioma completo.
Este repositorio es un puerto de RMC con comentarios adicionales. Cuenta con un punto de referencia de modelado de lenguaje de palabras de pleno derecho frente a LSTM tradicional.
Admite cualquier conjunto de datos de texto basado en token de palabras arbitrario, incluido Wikitext-2 y Wikitext-103.
Los modelos RMC y LSTM admiten Softmax adaptativo para un uso de memoria de vocabulario mucho más bajo de un conjunto de datos de vocabulario grande. RMC admite DataParallel de Pytorch, por lo que puede experimentar fácilmente con una configuración de múltiples GPU.
Los códigos de referencia tienen un ejemplo de modelo de modelo de lenguaje de palabras pytorch oficial
También presenta una tarea sintética más lejana del documento (ver más abajo).
Pytorch 0.4.1 o posterior (probado en 1.0.0) y Python 3.6
python train_rmc.py --cuda para entrenamiento completo y prueba de RMC con GPU.
python train_rmc.py --cuda --adaptivesoftmax --cutoffs 1000 5000 20000 si usa un conjunto de datos de vocabulario grande (como Wikitext-103) para adaptarse a todos los tensores en el VRAM.
python generate_rmc.py --cuda para generar oraciones del modelo entrenado.
python train_rnn.py --cuda para el entrenamiento completo y la prueba de prueba de RNN tradicional con GPU.
Todos los hiperparámetros predeterminados de RMC y LSTM son los resultados de un experimento de dos semanas usando Wikitext-2.
Probado con Wikitext-2 y Wikitext-103. Wikitext-2 está agrupado.
Cree una subcarpeta adentro ./data y coloque Word-Level train.txt , valid.txt y test.txt dentro de la subcarpeta.
Especifique --data=(subfolder name) y está listo para comenzar.
El código realiza la tokenización en la primera carrera de entrenamiento, y el corpus se guarda como pickle . El código cargará el archivo pickle después de la primera ejecución.
Tanto RMC como LSTM tienen ~ 11m parámetros. Consulte el código de capacitación para obtener detalles sobre hiperparámetros.
| Modelos | Perplejidad válida | Examen de la prueba | Pase hacia adelante MS/Batch (Titan XP) | Pase hacia adelante MS/Batch (Titan V) |
|---|---|---|---|---|
| LSTM (CUDNN) | 111.31 | 105.56 | 26 ~ 27 | 40 ~ 41 |
| LSTM (para bucle) | Igual que Cudnn | Igual que Cudnn | 30 ~ 31 | 60 ~ 61 |
| RMC | 112.77 | 107.21 | 110 ~ 130 | 220 ~ 230 |
RMC puede alcanzar un rendimiento comparable a LSTM (con una búsqueda pesada de hiperparameter), pero resulta que el RMC es muy lento. La autoatención de múltiples cabezas en cada paso de tiempo puede ser el culpable aquí. El uso de LSTMCell con For Loop (que es más "justo" de referencia para RMC) ralentiza el pase hacia adelante, pero aún es mucho más rápido.
Tenga en cuenta también que el hiperparámetro para RMC es el peor de los casos en términos de velocidad, ya que utilizó una sola ranura de memoria (como se describe en el documento) y no se benefició de un intercambio de peso en términos de filas de la memoria múltiple.
Es interesante observar que aquí es que la velocidad es más lenta en Titan V que Titan XP. La razón podría ser que los modelos son relativamente pequeños y el modelo llama a pequeñas operaciones lineales con frecuencia.
Tal vez Titan XP (~ 1,900MHz de velocidad del reloj CUDA desbloqueada frente a los beneficios de 1,335MHz de Titan V) de este tipo de carga de trabajo. O tal vez la latencia de lanzamiento del núcleo CUDA de Titan V es mayor para el OPS en el modelo.
No soy un experto en detalles de CUDA. ¡Comparta sus resultados!
Los parámetros de atención tienden a sobrepasar el wikitext-2. Reducir los hiperparparmetros para la atención (key_size) puede combatir el sobreajuste.
Aplicar abandono en el logit de salida antes del Softmax (como el LSTM One) ayudó a prevenir el sobreajuste.
| incrustación y tamaño de la cabeza | # cabezas | Capas MLP de atención | tamaño clave | abandonado en la salida | ranuras de memoria | prueba de personas |
|---|---|---|---|---|---|---|
| 128 | 4 | 3 | 128 | No | 1 | 128.81 |
| 128 | 4 | 3 | 128 | No | 1 | 128.81 |
| 128 | 8 | 3 | 128 | No | 1 | 141.84 |
| 128 | 4 | 3 | 32 | No | 1 | 123.26 |
| 128 | 4 | 3 | 32 | Sí | 1 | 112.4 |
| 128 | 4 | 3 | 64 | No | 1 | 124.44 |
| 128 | 4 | 3 | 64 | Sí | 1 | 110.16 |
| 128 | 4 | 2 | 64 | Sí | 1 | 111.67 |
| 64 | 4 | 3 | 64 | Sí | 1 | 133.68 |
| 64 | 4 | 3 | 32 | Sí | 1 | 135.93 |
| 64 | 4 | 3 | 64 | Sí | 4 | 137.93 |
| 192 | 4 | 3 | 64 | Sí | 1 | 107.21 |
| 192 | 4 | 3 | 64 | Sí | 4 | 114.85 |
| 256 | 4 | 3 | 256 | No | 1 | 194.73 |
| 256 | 4 | 3 | 64 | Sí | 1 | 126.39 |
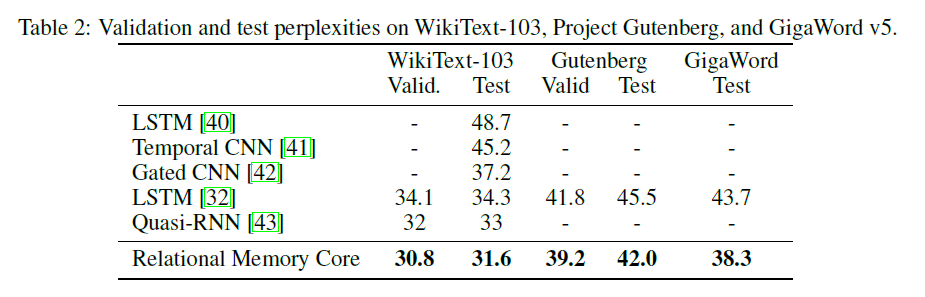
El papel RMC original presenta los resultados de Wikitext-103 con un modelo más grande y tamaño por lotes (6 Tesla P100, cada uno con 64 lotes de tamaño, por lo que un total de 384. Ouch).
El uso de un Softmax completo explota fácilmente el VRAM. Usar --adaptivesoftmax es muy recomendable. Si se usa --adaptivesoftmax , --cutoffs deben proporcionarse correctamente. Consulte la descripción original de la API
No tengo ese hardware y mi recurso es demasiado limitado para hacer los experimentos. ¡Resultado de referencia, o cualquier otra contribución es muy bienvenida!
El objetivo de la tarea es: dada k etiquetado aleatoriamente (de 1 a k) vectores d-dimensionales, identifique cuál es el enésimo vector más lejano del vector M. (la respuesta es un entero de 1 a k.)
La tarea específica en el documento es: dada 8 vectores de 16 dimensiones etiquetados, ¿cuál es el enésimo vector más alejado del vector m? Los vectores están etiquetados al azar, por lo que el modelo tiene que reconocer que el vector MTH es el vector marcado como M en oposición al vector en la posición MTH en la entrada.
La entrada al modelo comprende 8 vectores de 40 dimensiones para cada ejemplo. Cada uno de estos vectores de 40 dimensiones está estructurado así:
[(vector 1) (label: which vector is it, from 1 to 8, one-hot encoded) (N, one-hot encoded) (M, one-hot encoded)]
python train_nth_farthest.py --cuda para entrenamiento y prueba en la décima tarea más lejana con GPU (s).
Esto utiliza la clase RelationalMemory en relational_rnn_general.py , que es una versión de relational_rnn_models.py sin el código específico de modelado del lenguaje.
Consulte train_nth_farthest.py para obtener detalles sobre los valores de hiperparameter. Estos se toman del Apéndice A1 en el documento y de la implementación del soneto cuando los valores del hiperparameter no se dan en el documento.
Nota: Se generan nuevos ejemplos por época como en la implementación del soneto. Esto parece ser consistente con el documento, que no especifica el número de ejemplos utilizados.
El modelo ha sido entrenado con una sola GPU de Titan XP durante una eternidad hasta que alcanza el 91% de precisión de la prueba. A continuación se presentan los resultados con 3 ejecuciones independientes: 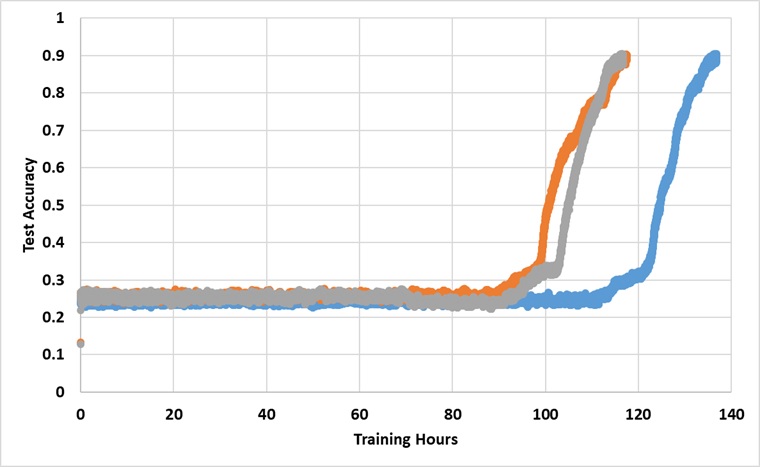
El modelo rompe la barrera del 25% si se entrena lo suficiente, pero el tiempo del reloj de pared es aproximadamente más de 2 ~ 3x más largo que los reportados en el papel.
Experimentar con diferentes hiperparámetros