Este proyecto intenta resolver el problema del reconocimiento de entidades de nombres chinos utilizando una variedad de modelos diferentes (incluidos HMM, CRF, BI-LSTM, BI-LSTM+CRF). El conjunto de datos utiliza los datos de currículum recopilados en el documento ACL 2018 NER chino con Lattice LSTM. El formato de los datos es el siguiente. Cada línea está compuesta de una palabra y su anotación correspondiente. El conjunto de anotaciones es bioes y las oraciones están separadas por una línea en blanco.
美 B-LOC
国 E-LOC
的 O
华 B-PER
莱 I-PER
士 E-PER
我 O
跟 O
他 O
谈 O
笑 O
风 O
生 O
Este conjunto de datos se encuentra en la carpeta ResumeNER en el directorio del proyecto.
Aquí hay cuatro modelos diferentes y la precisión de los resultados de predicción de estos cuatro modelos (tomando lo mejor):
| MMM | CRF | Bilstm | Bilstm+CRF | Conjunto | |
|---|---|---|---|---|---|
| Tasa de recuperación | 91.22% | 95.43% | 95.32% | 95.72% | 95.65% |
| Exactitud | 91.49% | 95.43% | 95.37% | 95.74% | 95.69% |
| Puntaje F1 | 91.30% | 95.42% | 95.32% | 95.70% | 95.64% |
La última columna de conjunto combina los resultados de predicción de estos cuatro modelos y utiliza el método de "votación" para obtener los resultados finales de predicción.
(Los tres indicadores del conjunto no son tan buenos como BilstM+CRF. Se puede decir que en el proceso del conjunto, fueron los otros tres modelos los que arrastraron BilstM+CRF)
Para una salida específica, puede ver el archivo output.txt .
Primero instale las dependencias:
pip3 install -r requirement.txt
Después de la instalación, úselo directamente
python3 main.py
Puede entrenar y evaluar el modelo. El modelo de evaluación imprimirá la precisión del modelo, el retiro, el valor de puntaje F1 y la matriz de confusión. Si desea modificar los parámetros del modelo o los parámetros de entrenamiento relevantes, puede configurarlo en el archivo ./models/config.py .
Después de la capacitación, si desea cargar y evaluar el modelo, ejecute el siguiente comando:
python3 test.pyAquí hay una breve introducción a estos modelos (la página web de GitHub no admite muy bien las fórmulas matemáticas, y las partes involucradas en las fórmulas no se pueden mostrar normalmente. Mi blog tiene una introducción más detallada a estos modelos y código):
El modelo de Markov oculto describe el proceso de generar aleatoriamente secuencias aleatorias de estado no observables a partir de una cadena de Markov oculta, y luego generar una observación de cada estado para generar una secuencia aleatoria de observación (método de aprendizaje estadístico de Li Hang). El modelo de Markov oculto está determinado por la distribución del estado inicial, la matriz de probabilidad de transición de estado y la matriz de probabilidad observada.
El reconocimiento de entidades de nombres puede considerarse esencialmente como un problema de etiquetado de secuencia. Al usar HMM para resolver el problema de etiquetado de secuencia del reconocimiento de entidad nombrado, lo que podemos observar es la secuencia compuesta de palabras (secuencia de observación), y lo que no podemos observar es la etiqueta correspondiente a cada palabra (secuencia de estado).
La distribución del estado inicial es la probabilidad de inicialización de cada etiqueta, y la matriz de probabilidad de transición de estado es la probabilidad de transferir de una determinada etiqueta a la siguiente etiqueta (es decir, si la etiqueta de la palabra anterior es $ tag_i $, la probabilidad de que la etiqueta de la palabra siguiente sea $ tag_j $ es
Bajo cierta marca, la probabilidad de generar una determinada palabra.
El proceso de entrenamiento del modelo HMM corresponde a los problemas de aprendizaje del modelo de Markov oculto (método de aprendizaje estadístico de Li Hang),
De hecho, es estimar los tres elementos del modelo basados en los datos de capacitación basados en el método de máxima probabilidad, a saber, la distribución de estado inicial, la matriz de probabilidad de transición de estado y la matriz de probabilidad de observación mencionada anteriormente. Una vez entrenado el modelo, el modelo se usa para decodificar, es decir, para una secuencia de observación dada, es encontrar su secuencia de estado correspondiente. Aquí está para encontrar la anotación correspondiente para cada palabra en la oración para una oración dada. Para este problema de decodificación, usamos el algoritmo Viterbi.
Para obtener detalles específicos, consulte el archivo de models/hmm.py .
Hay dos supuestos en el modelo HMM: una es que los valores de observación de salida son estrictamente independientes, y el otro es que el estado actual solo está relacionado con el estado anterior durante la transición del estado. Es decir, en el escenario del reconocimiento de entidades de nombres, HMM cree que cada palabra en la oración observada es independiente entre sí, y la etiqueta del momento actual solo está relacionada con la etiqueta del momento anterior. Pero, de hecho, el reconocimiento de entidades de nombres a menudo requiere más características, como parte del habla, el contexto de palabras, etc. Al mismo tiempo, la etiqueta del momento actual debe asociarse con la etiqueta del momento anterior y el siguiente momento. Debido a la existencia de estos dos supuestos, es obvio que el modelo HMM es defectuoso para resolver el problema del reconocimiento de entidad nombrado.
Los campos aleatorios condicionales no solo pueden expresar la dependencia entre las observaciones, sino también representar la dependencia compleja entre la observación actual y los estados anteriores y posteriores, lo que puede superar efectivamente los problemas que enfrenta el modelo HMM.
Para establecer un campo aleatorio condicional, primero necesitamos definir un conjunto de funciones de características, cada función de características en el conjunto toma la secuencia de anotación como entrada y las características extraídas como salida. Suponga que el conjunto de funciones es:
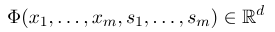
donde $ x = (x_1, ..., x_m) $ representa la secuencia de observación, y $ s = (s_1, ......, s_m) $ representa la secuencia de estado. El campo aleatorio condicional utiliza un modelo lineal logarítmico para calcular la probabilidad condicional de la secuencia de estado bajo una secuencia de observación dada:
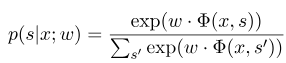
donde $ S^{'} $ es la secuencia de todos los estados posibles, y $ W $ es el parámetro del modelo de campo aleatorio condicional, que puede considerarse como el peso de cada función de características. El entrenamiento del modelo CRF es en realidad la estimación del parámetro $ W $. Supongamos que tenemos $ n $ marcados datos $ {(x^i, s^i)} _ {i = 1}^n $,
Entonces, la forma de regularización de su función de verificación log-probable es la siguiente:
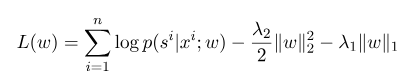
Entonces, el parámetro óptimo $ W^*$ es:
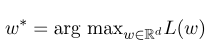
Después de que se complete el entrenamiento del modelo, para la secuencia de observación dada $ x $, su secuencia de estado óptima correspondiente debería ser:
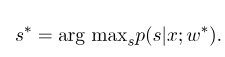
Es similar a HMM al decodificar, y el algoritmo Viterbi también se puede usar.
Para obtener detalles específicos, consulte el archivo de models/crf.py .
Además de los dos métodos anteriores basados en modelos de gráficos de probabilidad, LSTM a menudo se usa para resolver el problema de etiquetado de secuencia. A diferencia de HMM y CRF, LSTM se basa en la fuerte capacidad de ajuste no lineal de las redes neuronales. Durante el entrenamiento, las muestras se aprenden a través de transformaciones no lineales complejas en un espacio de alta dimensión, y luego usan esta función para predecir la anotación de cada token para la muestra especificada. A continuación se muestra un diagrama esquemático de anotación de secuencia utilizando LSTM bidireccional (bidireccional puede capturar mejor las dependencias entre secuencias):
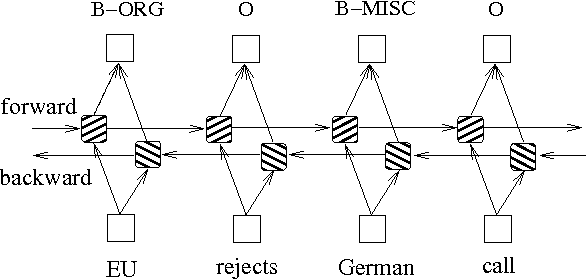
La implementación del modelo de etiquetado de secuencia basada en LSTM bidireccional puede ver models/bilstm.py .
La ventaja de LSTM es que puede aprender la dependencia entre las secuencias de observación (palabras de entrada) a través de configuraciones bidireccionales. Durante el proceso de entrenamiento, LSTM puede extraer automáticamente las características de la secuencia de observación basada en el objetivo (como las entidades de identificación), pero la desventaja es que no puede aprender la relación entre las secuencias de estado (etiquetas de salida). Debe saber que en la tarea de reconocimiento de entidades de nombres, existe una cierta relación entre las etiquetas. Por ejemplo, una etiqueta B (que representa el comienzo de una entidad) no será seguida por otra etiqueta B. Por lo tanto, cuando LSTM resuelve tareas de etiquetado de secuencia como NER, aunque puede eliminar la ingeniería de características complicada, también tiene la desventaja de no poder aprender el contexto de etiquetado.
Por el contrario, la ventaja de CRF es que puede modelar estados implícitos y aprender las características de las secuencias estatales, pero su desventaja es que requiere la extracción manual de las características de secuencia. Entonces, el enfoque general es agregar otra capa de CRF detrás del LSTM para obtener las ventajas de ambos.
Para una implementación específica, consulte models/bilstm_crf.py
El problema del OOV (fuera del vocabulario) debe manejarse en el modelo HMM, es decir, algunas palabras en el conjunto de pruebas no están en el conjunto de entrenamiento. En este momento, la probabilidad de varios estados correspondientes a OOV no se puede encontrar a través de la matriz de probabilidad de observación. Para lidiar con este problema, la distribución de probabilidad del estado correspondiente a OOV se puede establecer en una distribución uniforme.
Cuando los tres parámetros de HMM (es decir, la matriz de probabilidad de transición de estado, la matriz de probabilidad de observación y la matriz de probabilidad de estado inicial) se usan para la estimación utilizando el método de aprendizaje supervisado, si algunos términos nunca aparecen, entonces la posición correspondiente del término es 0. Al decodificar el algoritmo VITERBI, el proceso de cálculo de la calculación debe multiplicar estos valores. Entonces, si hay términos con 0, la probabilidad de toda la ruta también se convertirá en 0. Además, es probable que múltiples multiplicaciones de baja probabilidad durante el proceso de decodificación causen bajo flujo. Para resolver estos dos problemas, asignamos un número muy pequeño a aquellos términos que nunca han aparecido (como 0.00000001). Al mismo tiempo, al decodificar, asignamos los tres parámetros del modelo al espacio logarítmico, que no solo puede evitar el bajo flujo, sino que también simplificamos la operación de multiplicación.
Antes de usar los datos de entrenamiento y los datos de prueba como entrada al modelo en CRF, ¡debe usar funciones de características para extraer funciones!
Para el modelo BI-LSTM+CRF, puede consultar: Arquitecturas neuronales para el reconocimiento de entidades con nombre, y puede centrarse en la definición de la función de pérdida en él. El cálculo de las funciones de pérdida en el código utiliza un método similar a la programación dinámica, que no es fácil de entender. Aquí recomendamos mirar los siguientes blogs: