การใช้การจำลองสำหรับค่าอินพุตที่กำหนดแอปพลิเคชัน R มันวาวนี้แสดงให้เห็นถึงประสิทธิภาพการวินิจฉัย (ซึ่งวัดโดยอัตราการตรวจจับหรือพื้นที่ที่ถูกต้องภายใต้เส้นโค้ง) การเปลี่ยนแปลงที่เกี่ยวข้องกับความแตกต่างเฉลี่ยของค่าเฉลี่ย ( SMD ) ความแตกต่างของขนาดผลกระทบระหว่างกรณีเงื่อนไขเดี่ยว (เมื่อเปรียบเทียบโดยตรงกับการควบคุม)
แอปพลิเคชันสามารถใช้งานออนไลน์ได้ (เพื่อเปิดในเว็บเบราว์เซอร์ใด ๆ ): https://gasparl.shinyapps.io/esdi/
อย่างไรก็ตามมันยังง่ายที่จะเรียกใช้จากพีซีของคุณ คุณเพียงแค่ต้องเรียกใช้คำสั่งต่อไปนี้ใน r :
shiny :: runGitHub( " esdi " , " gasparl " )` สำหรับทางเลือกหลังนี้หากคุณยังไม่มีคุณต้องติดตั้ง R แล้วติดตั้งแพ็คเกจ shiny ภายใน R EG โดยป้อน install.packages("shiny") ลงในคอนโซล จากนั้นคัดลอก Line shiny::runGitHub("esdi", "gasparl") เช่นในคอนโซลและกด Enter ส่วนประกอบที่จำเป็นจะถูกดาวน์โหลดโดยอัตโนมัติและแอปพลิเคชันจะเปิดขึ้นในหน้าต่างใหม่
ในที่สุดในการใช้แอปพลิเคชันได้ตลอดเวลาโดยไม่ต้องเข้าถึงอินเทอร์เน็ตคุณสามารถดาวน์โหลดที่เก็บทั้งหมด (หรือเพียงแค่ app.r ) และเรียกใช้รหัสในไฟล์ app.r สำหรับสิ่งนี้คุณจะต้องติดตั้งแพ็คเกจ R ทั้งหมดที่ใช้ในรหัส (แสดงในบรรทัดแรก)
หากต้องการเข้าใจสาระสำคัญของแอปพลิเคชันอย่างรวดเร็วดู ส่วนตัว อย่างด้านล่างหรือดู พื้นหลัง สำหรับแรงจูงใจทั่วไป สิ่งต่อไปนี้นี่คือคำอธิบายทางเทคนิคโดยละเอียด
การตั้งค่าเพียงอย่างเดียวที่มีอิทธิพลต่อความสัมพันธ์ที่สำคัญ SMD-diagnostics คือ (อัตราส่วนของ) ส่วนเบี่ยงเบน มาตรฐาน (SDS) ของค่าตัวทำนายสำหรับ กรณี และสำหรับ การควบคุม ซึ่งเป็นตัวแทนของ SD ที่สันนิษฐานโดยทั่วไปสำหรับข้อมูลจากกรณีบวกและข้อมูลจากการ ควบคุม ตามลำดับ (อีกครั้งสำหรับคำอธิบายเพิ่มเติม SDS ควรประเมินตาม SDS ทั่วไปสำหรับกรณีและการควบคุมในพื้นที่การวิจัยที่กำหนด อย่างไรก็ตามความแตกต่างของ SD มีผลกระทบค่อนข้างน้อยต่อผลลัพธ์และสำหรับกรณีส่วนใหญ่ (ที่ SD ไม่เป็นที่รู้จักหรือไม่สามารถประมาณได้ง่าย) อาจสันนิษฐานได้ว่าการออกจากการตั้งค่าเริ่มต้น ( 1 สำหรับ SDS ทั้ง สอง ) จะยังคงให้ผลลัพธ์ที่ถูกต้องโดยประมาณ กล่าวอีกนัยหนึ่งการตั้งค่าเริ่มต้นของซอฟต์แวร์นี้อาจใช้ได้กับสถานการณ์ส่วนใหญ่
ขึ้นอยู่กับ SDS ที่กำหนดวิธีการของตัวอย่างจะถูกคำนวณโดยอัตโนมัติสำหรับแต่ละ SMD ที่ระบุภายใต้การตั้งค่าอื่น ๆ หมายเหตุ: หากต้องการสั้น ๆ และยังหลีกเลี่ยงตัวย่อ SMD (ความแตกต่างของค่าเฉลี่ยมาตรฐาน) จะถูกระบุว่าเป็น "ขนาดเอฟเฟกต์" สำหรับตัวเลือกและฉลากพล็อตบนอินเทอร์เฟซ ชุดข้อมูลถูกสร้างขึ้นสำหรับวิธีการที่แตกต่างกันทั้งหมด (โดยใช้ SDS คงที่ทั้งสอง) ที่มีการแจกแจงแบบปกติที่สมบูรณ์แบบ ข้อกำหนดของ SMDS นั้นค่อนข้างตรงไปตรงมา: ค่าเริ่มต้นค่าสุดท้ายและขั้นตอนจะต้องได้รับ ตัวอย่างเช่นการเริ่มต้น 0.2 ปลาย 0.6 และขั้นตอน 0.1 จะกำหนด SMDS ต่อไปนี้: 0.2 , 0.3 , 0.4 , 0.5 , 0.6 ขั้นตอนที่เล็กกว่า (หรือจุดเริ่มต้นที่ห่างไกลกว่า) หมายถึง datapoints มากขึ้นในการคำนวณและดังนั้นการตั้งค่าเหล่านี้สามารถเพิ่มเวลาการคำนวณได้อย่างมาก
มันเป็นสิ่งสำคัญที่จะต้องคำนึงถึงความแตกต่างระหว่าง (a) SMD ระหว่างเงื่อนไขเดียว ("กรณีที่ 1" เทียบกับ "กรณี 2") และ (b) SMD ระหว่างกรณีและการควบคุมของเงื่อนไขเดียว ("กรณี" เทียบกับ "การควบคุม") คนแรก (a) บ่งบอกถึงความแตกต่างในประสิทธิภาพการวินิจฉัยระหว่างวิธีการวินิจฉัยสองวิธี (เช่นวิธีเก่าและวิธีการที่ได้รับการปรับปรุงใหม่) ในขณะที่วิธีที่สอง (b) เป็นเพียงการวัดทางเลือกสำหรับประสิทธิภาพการวินิจฉัยภายในวิธีการวินิจฉัยที่มีขนาดใหญ่กว่า อัตราการตรวจจับที่ถูกต้องและพื้นที่ขนาดใหญ่ภายใต้เส้นโค้ง)
การควบคุม "กรณี 1" กับ "SMD เริ่มต้นแสดงถึงประสิทธิภาพการวินิจฉัยที่สันนิษฐานของวิธีการที่จะปรับปรุง (วิธีที่ 1) (หมายเหตุ: เป็นไปได้ แต่มีเหตุผลเล็กน้อยที่จะรวมศูนย์สำหรับค่าเริ่มต้นเว้นแต่เพื่อการสาธิตเนื่องจากนั่นหมายความว่าวิธีการที่ 1 ดำเนินการในระดับโอกาสดังนั้นมัน จึง ไร้ประโยชน์ในสถานที่แรก) พล็อตแสดงถึงประสิทธิภาพการวินิจฉัย (วิธีการ 2 ของกรณีที่ 2 (หมายเหตุ: เพื่อความชัดเจนมันเป็นเรื่องดีเสมอที่จะรักษาค่าเริ่มต้นของ "กรณี 1" เทียบกับ "กรณี 2" SMD ที่ศูนย์ซึ่งแสดงให้เห็นถึงจุดเริ่มต้นที่ยังไม่มีความแตกต่างระหว่างสองวิธี) จากนั้นมันสามารถเห็นได้ว่าการเพิ่มขึ้นของการเริ่มต้น แอปพลิเคชัน.
ค่าจะถูกแสดงในสองวิธีที่แตกต่างกัน: ความแม่นยำทั้งหมด และตาม ความแม่นยำที่ได้รับ ความแม่นยำที่ได้รับนั้นคำนวณได้ง่ายๆเป็นความแม่นยำทั้งหมดลบค่าเริ่มต้น (วิธีการ 1) ความแม่นยำ พล็อตที่รวมกันมีทั้งสองประเภทในขณะที่แผนการย่อยแสดงประเภทเหล่านี้แยกกันและอาจมีการสำรวจแบบโต้ตอบโดยการโฉบข้ามเส้นด้วยเคอร์เซอร์เพื่ออ่านค่าที่แม่นยำของ SMDS และความถูกต้องที่จุดที่กำหนดบนพล็อต (ดู ส่วนตัว อย่างด้านล่าง)
เนื่องจากขนาดตัวอย่างไม่สิ้นสุดการแจกแจงแบบปกติจึงไม่สมบูรณ์แบบอย่างแท้จริงดังนั้นจึงมีการเบี่ยงเบนเล็กน้อยในผลลัพธ์ SMD ที่คำนวณได้เมื่อเทียบกับการตั้งค่า SMD ที่กำหนด: ตัวอย่างเช่น SMD เริ่มต้นหนึ่งครั้งอาจได้รับเป็น 0.5 ในการตั้งค่า แต่ผลลัพธ์ที่แท้จริงอาจเป็นเช่น 0.51 ขนาดตัวอย่าง (จำนวน datapoints ที่สร้างขึ้น) สามารถตั้งค่าภายใต้ Sample size ฉลาก: จำนวนที่มากขึ้นนำไปสู่เวลาการคำนวณที่เพิ่มขึ้นบ้าง แต่ผลลัพธ์ที่แม่นยำยิ่งขึ้น ขนาดตัวอย่างประมาณ 4000 มักจะให้ความแม่นยำสูงถึงสองเศษส่วนในขณะที่แคลิฟอร์เนีย 15000 อาจแม่นยำถึงสามตัวเลขเศษส่วน ที่สำคัญโดยไม่คำนึงถึงขนาดตัวอย่าง (และการติดต่อของการตั้งค่าและผลลัพธ์) ความสัมพันธ์ของ SMD และการวินิจฉัยสำหรับผลลัพธ์ที่กำหนดนั้นแน่นอนและถูกต้องเสมอ
การตั้งค่าพล็อตเกี่ยวข้องกับการพรรณนาข้อมูลและควรอธิบายตนเอง ค่าทั้งหมดสำหรับการคำนวณพล็อตมีอยู่ภายใต้แท็บตารางในตารางข้อมูลแบบโต้ตอบ
การวิเคราะห์พลังงานในอนาคต ( เบื้องต้น ) เพื่อกำหนดขนาดตัวอย่างที่ต้องการเป็นสิ่งสำคัญสำหรับการทดลองเชิงพฤติกรรม (เช่น Perugini, 2018) ในการพิจารณาผลกระทบที่น้อยที่สุดของความสนใจที่จำเป็นสำหรับการวิเคราะห์พลังงานวิธีที่เหมาะสมที่สุดคือต้องพึ่งพาเหตุผลที่มีวัตถุประสงค์ (Lakens, 2013; Lakens et al, 2018) ตัวอย่างเช่นในการเปรียบเทียบวิธีการวินิจฉัยที่แตกต่างกันสองวิธีเราอาจพิจารณาถึงผลกระทบของชีวิตจริงของการเพิ่มขึ้นของอัตราการตรวจจับโรคที่ถูกต้องที่เกี่ยวข้องกับค่าใช้จ่ายของขนาดตัวอย่างที่จำเป็นในการแสดงหลักฐานทางสถิติสำหรับการเพิ่มขึ้น นักวิจัยอาจทำการตัดสินใจอย่างรอบคอบและระมัดระวังว่ามันคุ้มค่าที่จะรวบรวมพูดผู้เข้าร่วม 120 คนเพื่อตรวจจับการเพิ่มขึ้นอย่างน้อย 8% ในการตรวจจับความแม่นยำ: การเพิ่มขึ้น 2% หรือ 0.1% อาจมีประโยชน์ในชีวิตจริงที่สำคัญ แต่เนื่องจากทรัพยากรที่ จำกัด จึงไม่คุ้มค่าที่จะรวบรวมขนาดตัวอย่างที่ใหญ่กว่า
อย่างไรก็ตามความหมายในทางปฏิบัตินั้นไม่ได้ตรงไปตรงมาเสมอไปในการประเมิน ในสถานการณ์ที่เฉพาะเจาะจงหนึ่งในการออกแบบการทดลองวิธีการวินิจฉัยสองวิธีอาจถูกเปรียบเทียบอย่างถูกต้องโดยใช้กรณีเงื่อนไขเดี่ยวโดยไม่ต้องควบคุมการควบคุม (aka "พื้นฐาน" หรือ "เงื่อนไขเชิงลบ") เพื่อสำรองทรัพยากร สถานการณ์นี้สามารถเกิดขึ้นได้ในหลาย ๆ สาขาที่ใช้การจำแนกประเภทไบนารีซึ่งอาจเป็นลักษณะเฉพาะในการแพทย์ โรคสมมุติอาจได้รับการวินิจฉัยว่าเป็นมาตรการต่อเนื่อง X ซึ่งโดยทั่วไปจะสูงกว่าสำหรับผู้ที่เป็นโรคที่กำหนด (เช่นการชนเล็ก ๆ หรือสีแดงในการตอบสนองต่อการทดสอบทิ่มผิวหนัง; กรณีที่เป็นบวก) ในขณะที่มันเหมือนกันสำหรับคนที่มีสุขภาพดี ดังนั้นกรณีที่เป็นบวกสามารถตรวจพบได้ด้วยความแม่นยำบางอย่าง - แต่ไม่สมบูรณ์แบบเพราะการวัดบางอย่างมีความผิดพลาดในระดับหนึ่งและให้ค่าต่ำที่ผิดพลาดสำหรับกรณีบวกเช่นกัน หากมีคนเสนอการปรับปรุงขั้นตอนเพื่อให้ได้ค่าที่สูงขึ้นในการวัด X มันจะเป็นไปได้ที่จะเปรียบเทียบสองวิธีโดยตรงในกรณีที่เป็นบวกเท่านั้น: เนื่องจากการวัดจะคงที่ (ต่ำ) ในกรณีลบ (บุคคลที่มีสุขภาพดี) ค่าที่สูงขึ้นสำหรับกรณีบวกหมายความว่าขั้นตอนจะมีประสิทธิภาพการวินิจฉัยที่ดีขึ้น
ปัญหาที่นี่คือขนาดของเอฟเฟกต์สำหรับการคำนวณพลังงานที่อาจเกิดขึ้นระหว่างสองเงื่อนไขเชิงบวกซึ่งไม่มีความหมายโดยตรงสำหรับผลที่ตามมาในการวินิจฉัย ซอฟต์แวร์ปัจจุบันช่วยโดยการประมาณค่าสำหรับค่าประสิทธิภาพการวินิจฉัย (อัตราการตรวจจับที่ถูกต้องและพื้นที่ภายใต้เส้นโค้ง) สำหรับขนาดผลที่กำหนดระหว่างเงื่อนไขเชิงบวกเพียงอย่างเดียว
ซอฟต์แวร์นี้ได้รับแรงบันดาลใจจากการศึกษาการทดสอบข้อมูลแบบปกปิด (CIT): CIT สามารถเปิดเผยได้ว่าบุคคลนั้นรับรู้รายการ โพรบ ที่เกี่ยวข้อง (เช่นอาวุธสังหารที่เฉพาะเจาะจงที่ใช้ในอาชญากรรมล่าสุด) ในรายการอื่น ๆ ที่ ไม่ เกี่ยวข้อง (เช่นอาวุธอื่น ๆ ที่น่าเชื่อถือ) เนื่องจากบุคคลที่ไร้เดียงสาไม่รู้จักการสอบสวนที่เกี่ยวข้องการตอบสนองของพวกเขาจะไม่แตกต่างกันระหว่างโพรบและรายการที่ไม่เกี่ยวข้อง ดังนั้นขึ้นอยู่กับความแตกต่างของโพรบ-มินัส-อิลล์เรนซ์ ( PI ) ที่มีขนาดใหญ่ขึ้นผู้ที่มีความผิดสามารถแยกแยะได้จากผู้บริสุทธิ์ สิ่งสำคัญอย่างยิ่งเนื่องจาก PI อยู่ใกล้ศูนย์เสมอสำหรับผู้บริสุทธิ์การศึกษาจำนวนมากเปรียบเทียบ CIT รุ่นต่าง ๆ โดยใช้กลุ่มที่มีความผิดเท่านั้นด้วยความเข้าใจว่ากลุ่ม PI ขนาดใหญ่มีความหมายสำหรับรุ่นที่กำหนดหมายความว่าประสิทธิภาพการวินิจฉัยจะดีขึ้นโดยใช้เวอร์ชันนั้น (เช่นบุคคลที่มีความผิดมากขึ้น อย่างไรก็ตามความแตกต่างของค่าเฉลี่ยเลขคณิตระหว่างสองกลุ่มที่มีความผิด (หรือ SMD ที่เกี่ยวข้อง) ไม่มีความหมายที่สมเหตุสมผลจริง ๆ ดังนั้นจึงไม่สามารถใช้สำหรับการตัดสินใจที่มีการศึกษาเกี่ยวกับขนาดตัวอย่าง แท้จริงแล้ว 13 จาก 24 การศึกษาที่รวบรวมในการวิเคราะห์อภิมานเมื่อเร็ว ๆ นี้ (Lukács & Specker, 2020) ใช้การเปรียบเทียบเงื่อนไขเดี่ยวไม่มีรายงานการคำนวณพลังงานก่อนหน้านี้สำหรับขนาดตัวอย่างและแม้แต่การตีความขนาดเอฟเฟกต์ขึ้นอยู่กับที่มีชื่อเสียงของโคเฮน
ตอนนี้การวิเคราะห์อภิมานนี้ยังรายงาน SDS เฉลี่ย (จากการทดลอง 12 ครั้ง) สำหรับกรณี (กลุ่มที่มีความผิด) และการควบคุม (กลุ่มผู้บริสุทธิ์), 33.6 และ 23.5 ตามลำดับ-ดังนั้นสิ่งเหล่านี้อาจใช้ในแอปพลิเคชัน ESDI เป็นค่าอินพุตสำหรับ กรณี SD และ SD ควบคุม อย่างไรก็ตามการใช้ค่าเริ่มต้นของ 1 สำหรับ SDS ทั้งสองให้ผลลัพธ์ที่คล้ายกันมาก: โดยทั่วไปการรู้และการประมาณค่า SD ที่แม่นยำนั้นไม่สำคัญ (เว้นแต่ กรณี SD / อัตราส่วน SD ควบคุม อาจมีขนาดใหญ่หรือเล็กมาก)
การให้ 33.6 และ 23.5 สำหรับ กรณี SD และ การควบคุม SD , 4000 สำหรับ ขนาดตัวอย่าง และออกจากการตั้งค่าอื่น ๆ ทั้งหมดไม่เปลี่ยนแปลงพล็อตรวมหลักจะมีลักษณะเช่นนี้:
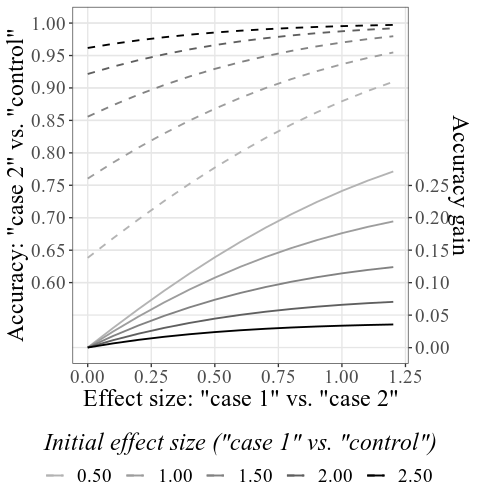
โปรดทราบว่า - ตามที่อธิบายไว้ในรายละเอียดภายใต้ วิธีการใช้ ส่วนด้านบน - ความถูกต้องเริ่มต้นจะถูกคำนวณตาม SMDS เริ่มต้นที่กำหนด (ดูฉลากด้านล่างภายใต้การตั้งค่าพล็อตฉลากนี้สามารถเปลี่ยนได้เพื่อแสดงความถูกต้องแทน SMDS) SMD ที่เกิดขึ้นอาจแตกต่างจาก SMDs เล็กน้อยที่ให้ไว้ในการตั้งค่าเนื่องจากกระบวนการจำลอง (อีกครั้งดู วิธีการใช้ สำหรับรายละเอียดทางเทคนิค)
การเพิ่มขึ้นของ ความแม่นยำทั้งหมด หรือ ความแม่นยำที่ได้รับ แบบอะนาล็อกในการทำงานของการเพิ่มขึ้นระหว่างเงื่อนไข (ความผิด 1 กับความผิด 2) SMD สามารถสำรวจแยกต่างหากบนแผนการย่อยแบบโต้ตอบ ตัวอย่างเช่นการโฉบเหนือบรรทัดดังที่แสดงด้านล่างฉลากที่ปรากฏแสดงว่าถ้าเราพบขนาดเอฟเฟกต์ (SMD) 0.601 ระหว่างผลลัพธ์ของสองกลุ่มที่มีความผิดได้รับความแม่นยำเริ่มต้นที่. 856 (อัตราการตรวจพบอย่างถูกต้อง หากเราสมมติว่าความแม่นยำเริ่มต้น (เช่นความแม่นยำโดยใช้วิธีการที่มีประสิทธิภาพการวินิจฉัยที่ด้อยกว่า) ของ CIT ประเภทนี้โดยทั่วไปประมาณ. 856 เราสามารถใช้ค่า SMD ในบรรทัดนี้สำหรับการคำนวณพลังงาน ตัวอย่างเช่นด้วย SMD 0.6 สำหรับพลัง 0.9 ขนาดตัวอย่างที่ต้องการต่อกลุ่มคือ 60 (สำหรับการทดสอบ t-unpaired กับ alpha = .05) ดังนั้นในการตรวจจับการเพิ่มขึ้นอย่างน้อย. 084 ในความแม่นยำในการตรวจจับต้องมีการรวบรวมทั้งหมด 120 คนสำหรับสองเงื่อนไขที่มีความผิด
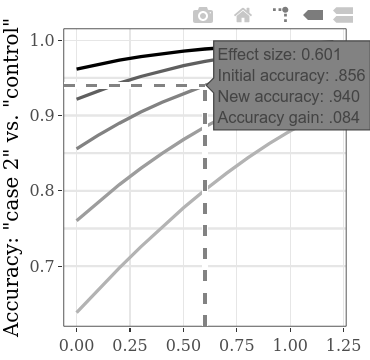
ความถูกต้องเริ่มต้นทางเลือกสามารถเปรียบเทียบได้โดยการเปลี่ยนไปใช้แท็บ subplots แบบโต้ตอบขนาดใหญ่ คลิกตัวเลือก "เปรียบเทียบข้อมูลบน Hover" บนพล็อตล่างและย้ายเคอร์เซอร์ตามแนวนอนตามพล็อต ตัวอย่างด้านล่างแสดงให้เห็นถึงความแม่นยำที่หลากหลายเมื่อ "กรณี 1" เทียบกับ "กรณี 2" SMD คือ 0.5 เนื่องจากเห็นได้ชัดในพล็อตตัวอย่างก่อนหน้าความแม่นยำเริ่มต้นที่ต่ำกว่าจะช่วยให้ได้รับความแม่นยำมากขึ้น
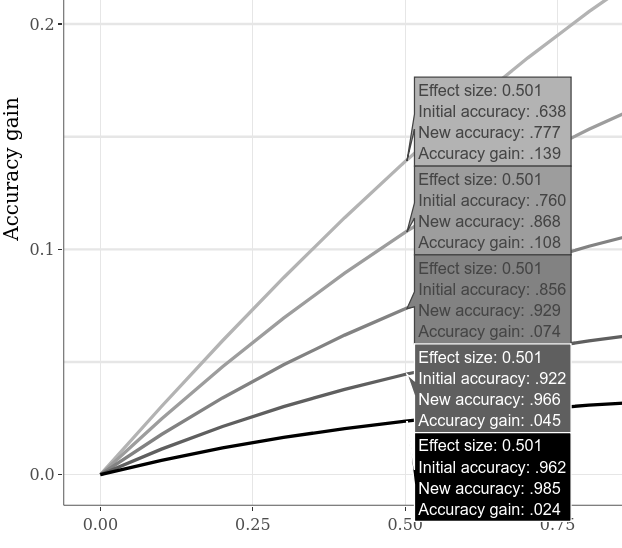
ในการสำรวจค่าเริ่มต้นเริ่มต้นมากขึ้นในเวลาเดียวกันการตั้งค่าขั้นตอนสำหรับ "กรณี 1" กับ "การควบคุม" SMD สามารถลดลงได้ซึ่งนำไปสู่บรรทัดที่มากขึ้นในพล็อต (และเวลาการคำนวณที่เพิ่มขึ้นค่อนข้างมาก) (ขั้นตอนสำหรับ "กรณี 1" กับ "กรณี 2" SMD จะส่งผลให้เกิด datapoint ในแนวนอนมากขึ้น)
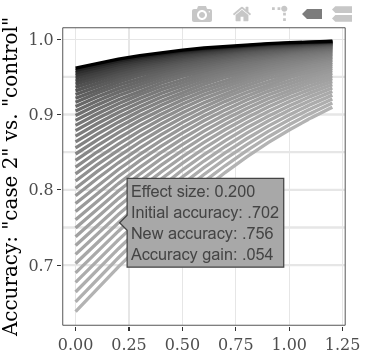
โดยค่าเริ่มต้นอัตราการตรวจจับที่ถูกต้องง่าย ๆ (จำนวนของวิชาที่จัดประเภทอย่างถูกต้องทั้งหมดหารด้วยจำนวนของทุกวิชา) จะแสดงสำหรับการวัด "ความแม่นยำ" เนื่องจากนี่อาจเป็นตัวบ่งชี้ประสิทธิภาพการวินิจฉัยที่ตรงไปตรงมาที่สุด สามารถเปลี่ยนไปเป็นพื้นที่ใต้เส้นโค้งภายใต้แท็บ "พล็อต" ในแผงด้านซ้าย ภายใต้แท็บเดียวกันฉลากพล็อตสามารถปรับแต่งได้
ฟังก์ชั่นพื้นฐานของซอฟต์แวร์สามารถตรวจสอบได้โดยใช้แพ็คเกจ shinytest เพื่อเรียกใช้ชุดทดสอบอัตโนมัติ (เช่นหลังจากการบริจาค) เพียงเรียกใช้ shinytest::recordTest("/path/to/directory/") - โดยที่ "/path/to/directory/" ควรถูกแทนที่ด้วยเส้นทางไปยังไดเรกทอรีแอปพลิเคชันเช่น "C:/apps/esdi/"
หากคุณมีคำถามใด ๆ หรือค้นหาปัญหาใด ๆ (ข้อบกพร่องคุณสมบัติที่ต้องการ) เขียนอีเมลหรือเปิดปัญหาใหม่
โคเฮน, เจ (1988) การวิเคราะห์พลังงานทางสถิติสำหรับวิทยาศาสตร์เชิงพฤติกรรม (2nd ed.) Hillsdale, NJ: Erlbaum
Lakens, D. (2013) การคำนวณและการรายงานขนาดเอฟเฟกต์เพื่ออำนวยความสะดวกวิทยาศาสตร์สะสม: ไพรเมอร์ที่ใช้งานได้จริงสำหรับการทดสอบ T และ ANOVAs Frontiers in Psychology, 4. https://doi.org/10.3389/fpsyg.2013.00863
Lakens, D. , Scheel, AM, & Isager, PM (2018) การทดสอบความเท่าเทียมกันสำหรับการวิจัยทางจิตวิทยา: บทช่วยสอน ความก้าวหน้าในวิธีการและการปฏิบัติในวิทยาศาสตร์จิตวิทยา, 1 (2), 259–269 https://doi.org/10.1177/2515245918770963
Perugini, M. , Gallucci, M. , & Costantini, G. (2018) ไพรเมอร์ที่ใช้งานได้จริงเพื่อการวิเคราะห์พลังงานสำหรับการออกแบบการทดลองอย่างง่าย การทบทวนระหว่างประเทศของจิตวิทยาสังคม, 31 (1), 20. https://doi.org/10.5334/irsp.181
อ้างถึงซอฟต์แวร์นี้เป็น:
Lukács, G. , & Specker, E. (2020) เรื่องการกระจาย: การวินิจฉัยและควบคุมการจำลองคอมพิวเตอร์ในการศึกษาการทดสอบข้อมูลที่ซ่อนอยู่ PLOS ONE, 15 (10), E0240259 https://doi.org/10.1371/journal.pone.0240259