Usando simulações para os valores de entrada fornecidos, esse aplicativo R brilhante mostra como a eficiência diagnóstica (medida por taxas de detecção correta ou áreas sob as curvas) muda em relação à diferença média padronizada ( SMD ) diferenças de tamanho de efeito entre os casos de condição única (quando são comparados diretamente para a falta de controles).
O aplicativo está disponível online (para ser simplesmente aberto em qualquer navegador da web): https://gasparl.shinyapps.io/esdi/
No entanto, também é fácil executá -lo no seu PC. Você só precisa executar o seguinte comando em r :
shiny :: runGitHub( " esdi " , " gasparl " )` Para esta última alternativa, se você ainda não os possui, precisará instalar R e instalar o pacote shiny no RE, por exemplo, inserindo install.packages("shiny") no console. Em seguida, copie a linha shiny::runGitHub("esdi", "gasparl") por exemplo, no console e pressione Enter. Os componentes necessários serão baixados automaticamente e o aplicativo será aberto em uma nova janela.
Por fim, para usar o aplicativo a qualquer momento sem acesso à Internet, você pode baixar o repositório inteiro (ou apenas app.r ) e executar o código no arquivo app.r. Para isso, você precisaria instalar todos os pacotes R usados no código (listados nas primeiras linhas).
Para entender rapidamente a essência da aplicação, consulte a seção de exemplo abaixo ou consulte o plano de fundo para a motivação geral. O que se segue aqui é uma explicação técnica detalhada.
As únicas configurações que influenciam a relação de diagnóstico de SMD-chave é a (proporção de desvios padrão (SDS) dos valores preditores para casos e controles , que representam o DP geralmente assumido para os dados de casos positivos e para os dados dos controles, respectivamente (novamente, para mais explicação, ver os antecedentes e exemplos abaixo). Os SDs devem ser estimados com base nos SDs típicos para casos e controles na área de pesquisa especificada. No entanto, as diferenças de SD têm relativamente pouco impacto nos resultados e, na maioria dos casos (onde o DP não é conhecido ou não pode ser facilmente estimado), pode -se supor que deixar as configurações padrão ( 1 para ambos os SDs) ainda fornecerá aproximadamente resultados corretos (a menos que o caso SD / controle SD possa ser muito grande ou muito pequeno). Em outras palavras, as configurações padrão deste software provavelmente são aplicáveis para a maioria dos cenários.
Com base nos SDs fornecidos, as médias das amostras são calculadas automaticamente para cada um dos SMDs especificados nas outras configurações. Nota: Para ser breve e, no entanto, evite a abreviação, o SMD (diferença média padronizada) é indicada como "tamanho do efeito" para os rótulos de opção e plotagem na interface. Os conjuntos de dados são gerados para todos os meios diferentes (usando os dois SDs constantes) com distribuição normal quase perfeita. A especificação do SMDS é bastante direta: um valor inicial, um valor final e uma etapa deve ser fornecida. Por exemplo, um início de 0.2 , uma extremidade de 0.6 e uma etapa de 0.1 definirá os seguintes SMDs: 0.2 , 0.3 , 0.4 , 0.5 , 0.6 . Etapa menor (ou mais distante e final) significa mais pontos de dados para calcular e, portanto, essas configurações podem aumentar substancialmente o tempo de cálculo.
É importante ter em mente a diferença entre (a) SMD entre as condições únicas ("Caso 1" vs. "Caso 2") e (b) o SMD entre o caso e o controle de uma única condição ("caso" vs. "Control"). The first one (a) is indicative of differences in diagnostic efficiency between two diagnostic methods (eg an old method and a new improved method), while the second one (b) is merely an alternative measurement for diagnostic efficiency within a given method (eg the diagnostic efficiency of the old method), and this latter is always in direct positive correlation with the other diagnostic efficiency measures (so larger "case" vs. "control" SMD always means larger rate de detecção correta e área maior sob a curva).
O SMD inicial "Caso 1" vs. "Control" representa as eficiências diagnósticas assumidas do método a ser melhorado (Método 1). (Nota: é possível, mas faz pouco sentido na prática incluir zero para o valor de início, a menos que para fins de demonstração, pois isso significaria que o método 1 execute no nível do acaso, por isso é inútil em primeiro lugar.) As parcelas representam o método aprimorado (método 2) " Caso" V. (Nota: Para maior clareza, é sempre bom manter o valor inicial do "Caso 1" vs. "Caso 2" SMD em zero, o que ilustra o ponto de partida em que ainda não há diferença entre os dois métodos. aplicativo.
Os valores são retratados de duas maneiras diferentes: como precisão total e à medida que a precisão obteve . A precisão obtida é calculada simplesmente como precisão total menos precisão inicial (método 1). O gráfico combinado contém os dois tipos, enquanto as subparcelas representam esses tipos separadamente e podem ser exploradas interativamente, pairando sobre as linhas com o cursor para ler os valores precisos de SMDs e precisão nos pontos fornecidos no gráfico (veja a seção de exemplo abaixo).
Como o tamanho da amostra não é infinito, a distribuição normal nunca pode ser verdadeiramente perfeita e, portanto, haverá pequenos desvios nos resultados calculados de SMD em comparação com as configurações de SMD fornecidas: por exemplo, um SMD inicial pode ser dado como 0.5 nas configurações, mas os resultados reais podem ser, por exemplo, 0.51 . O tamanho da amostra (número de pontos de dados gerados) pode ser definido no Sample size do rótulo: o número maior leva a um pouco de tempo de cálculo, mas resultados mais precisos. Um tamanho de amostra de cerca de 4000 normalmente dá precisão até dois dígitos fracionários, enquanto ca. 15000 pode ser preciso até três dígitos fracionários. É importante ressaltar que, independentemente do tamanho da amostra (e da correspondência de configurações e resultados), a relação do SMD e o diagnóstico para os resultados fornecidos é sempre exato e correto.
As configurações da plotagem estão relacionadas à representação dos dados e devem ser auto-explicativas. Todos os valores para o cálculo dos gráficos estão disponíveis na guia Tabela em uma tabela de dados interativos.
Análise prospectiva ( a priori ) para determinar o tamanho da amostra necessário é crucial para experimentos comportamentais (por exemplo, Perugini, 2018). Para determinar o menor efeito de interesse necessário para a análise de poder, a maneira ideal é confiar na justificativa objetiva (Lakens, 2013; Lakens et al, 2018). Por exemplo, para comparar dois métodos de diagnóstico diferentes, pode -se considerar as implicações da vida real de um determinado aumento na taxa de detecções corretas de uma doença em relação aos custos do tamanho da amostra necessário para mostrar evidências estatísticas para o aumento. Um pesquisador pode tomar a decisão informada e cuidadosa de que vale a pena coletar, digamos, 120 participantes para detectar um aumento de pelo menos 8% na precisão da detecção: um aumento de 2% ou até 0,1% também pode ter benefícios importantes da vida real, mas devido a recursos limitados, não vale a pena coletar os tamanhos de amostra muito maiores necessários para detectar alterações menores.
No entanto, a implicação prática nem sempre é tão direta para avaliar. Em um cenário específico no projeto experimental, dois métodos de diagnóstico podem ser comparados validamente usando casos de condição única, omitindo controles (também conhecidos como "linha de base" ou "condição negativa") para poupar recursos. Esse cenário pode ocorrer em qualquer um dos muitos campos que aplicam classificação binária, talvez mais caracteristicamente na medicina. Uma doença hipotética pode ser diagnosticada com uma medida contínua X , que geralmente é mais alta para pessoas com uma determinada doença (como um pequeno inchaço ou vermelhidão em reação a um teste de picada de pele; casos positivos), enquanto geralmente é o mesmo para pessoas saudáveis (como nenhuma reação ou pouca reação a um teste de picada da pele; casos negativos). Assim, casos positivos podem ser detectados com uma certa precisão - mas não perfeitamente, porque algumas das medições estão em certa medida e dão valores erroneamente baixos para casos positivos também. Se alguém propô uma melhora no procedimento para alcançar valores mais altos na medida X , seria possível comparar diretamente os dois métodos apenas em casos positivos: como a medida sempre será constante (baixa) em casos negativos (pessoas saudáveis), valores mais altos para casos positivos significa que o procedimento também terá melhor eficiência diagnóstica.
O problema aqui é que o tamanho do efeito para o cálculo potencial de potência está entre duas condições positivas, que não têm implicação direta para as consequências práticas no diagnóstico. O presente software ajuda a fornecer estimativas para valores de eficiência de diagnóstico (taxas de detecção corretas e áreas sob as curvas) para os tamanhos de efeito determinados apenas entre condições positivas.
Este software foi realmente inspirado em estudos de teste de informação oculta (CIT): o CIT pode revelar que uma pessoa reconhece um item de sonda relevante (por exemplo, uma arma de crimes específica usada em um crime recente) entre outros itens irrelevantes (por exemplo, outras armas plausíveis), com base em diferentes, por exemplo, respondendo à propensa comparada aos itens irrelevantes. Como as pessoas inocentes não reconhecem a investigação como relevante, suas respostas não diferem em média entre os itens de sonda e irrelevantes. Portanto, com base em diferenças maiores de sonda-minus-irlevante ( PI ), as pessoas culpadas podem ser distinguidas das inocentes. Fundamentalmente, como o PI está sempre em torno de zero para inocentes, muitos estudos comparam versões diferentes do CIT usando apenas grupos culpados, com o entendimento de que o grupo PI maior significa para uma determinada versão significa que a eficiência diagnóstica também será melhor usando essa versão (o IE mais culpado pode ser distinguido corretamente dos inocentes). No entanto, a diferença na média aritmética entre dois grupos culpados (ou o SMD relacionado) não tem realmente nenhuma implicação prática sensata e, portanto, não pode ser usada para uma decisão educada sobre o tamanho da amostra. De fato, 13 de 24 estudos coletados em uma meta-análise recente (Lukács & Specker, 2020) usaram comparação de condição única, nenhum relatou cálculo de energia prévio para tamanhos de amostra e até a interpretação de tamanhos de efeito foram baseados no famoso Cohen, mas no final dos benchmarks, sem significado prático direto (Cohen, 1988;
Agora, essa meta-análise também relatou SDs médias (com base em 12 experimentos) para casos (grupos culpados) e controles (grupos inocentes), 33.6 e 23.5 , respectivamente-para que estes possam ser usados na aplicação da ESDI como valores de entrada para o caso SD e controle SD . No entanto, o uso do valor padrão de 1 para ambos os SDs realmente fornece resultados muito semelhantes: em geral, conhecer e fornecer estimativas precisas de SD não é vital (a menos que a relação SD / controle SD possa ser muito grande ou muito pequena).
Dando o 33.6 e 23.5 para o caso SD e controle SD , 4000 para o tamanho da amostra e, deixando todas as outras configurações inalteradas, o enredo combinado principal ficará assim:
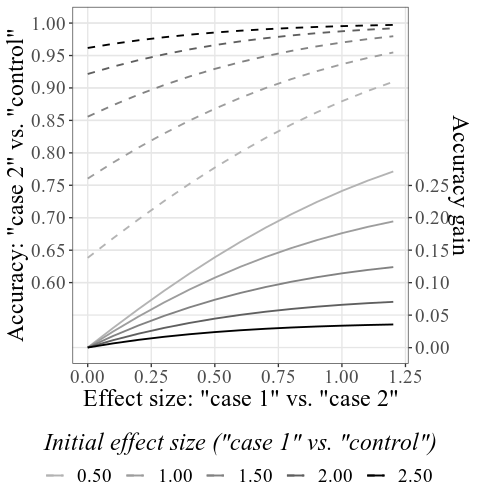
Observe que - conforme explicado em detalhes na seção Como usar acima - as precisões iniciais são calculadas com base nos SMDs iniciais fornecidos (consulte a etiqueta inferior; em Configurações da plotagem, esse rótulo pode ser alterado para exibir precisão em vez de SMDS). Os SMDs resultantes podem diferir ligeiramente dos SMDs fornecidos nas configurações, devido ao processo de simulação (novamente, veja como usar para obter detalhes técnicos).
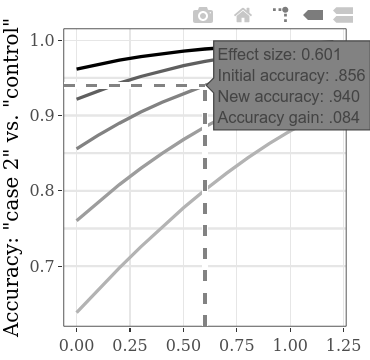
O aumento da precisão total ou da precisão análoga ganhou , na função do aumento na condição (culpada 1 vs. culpada 2) SMD, pode ser explorada separadamente nas subparcelas interativas. Por exemplo, pairando sobre a linha, como mostrado abaixo, o rótulo que aparece mostra que, se encontrarmos um tamanho de efeito (SMD) de 0,601 entre os resultados de dois grupos culpados, dada uma precisão inicial de 0,856 (taxa de detecção correta). Se assumirmos que a precisão inicial (ou seja, a precisão usando o método com a eficiência diagnóstica inferior) desse tipo de CIT é geralmente em torno de 0,856, podemos usar os valores de SMD nessa linha para cálculo de potência. Por exemplo, com o SMD 0,6, para uma potência de 0,9, o tamanho da amostra necessário por grupo é 60 (para um teste t não emparelhado com alfa = 0,05). Portanto, para detectar estatisticamente um aumento de pelo menos 0,084 na precisão da detecção, um total de 120 pessoas precisam ser coletadas para as duas condições de culpa.
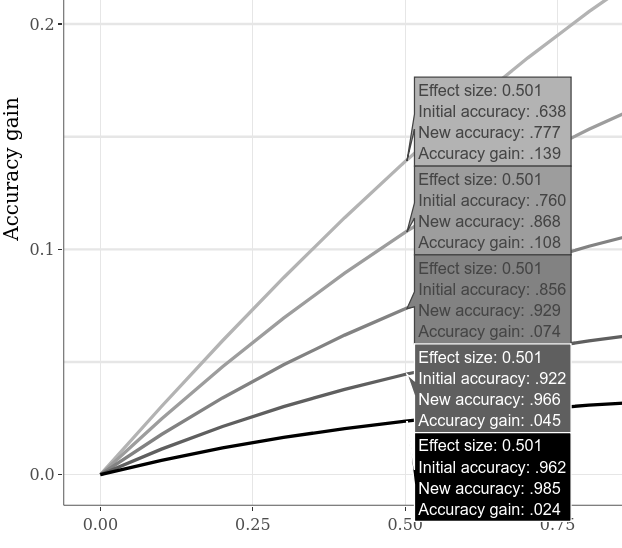
As precisões iniciais alternativas podem ser comparadas por, por exemplo, alternar com a guia Subparcelas interativas grandes , clicando na opção "Compare dados sobre o hover" no gráfico inferior e movendo o cursor horizontalmente ao longo do gráfico. O exemplo abaixo mostra vários ganhos de precisão quando o "Caso 1" vs. "Caso 2" SMD é 0,5. Como já era aparente nas parcelas de exemplo anterior, a menor precisão inicial sempre permite maior ganho de precisão.
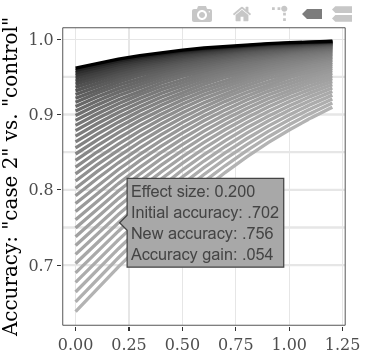
Para explorar mais valores iniciais iniciais ao mesmo tempo, a configuração da etapa para "Caso 1" vs. "Control" SMD pode ser reduzida, levando a mais linhas no gráfico (e para um pouco de tempo de cálculo aumentado). (A etapa para o "Caso 1" vs. "Caso 2" SMD resultará analogamente em mais dados horizontais.)
Por padrão, taxas simples de detecção correta (número de todos os sujeitos classificados corretamente divididos pelo número de todos os sujeitos) são exibidos para medição de "precisão", pois esse é provavelmente o indicador mais direto da eficiência diagnóstica. Ele pode ser alterado para área sob a curva na guia "Plot" no painel esquerdo. Na mesma guia, os rótulos de plotagem também podem ser personalizados.
A funcionalidade básica do software pode ser verificada usando o pacote shinytest para executar um processo de teste automatizado (por exemplo, após fazer contribuições). Basta executar shinytest::recordTest("/path/to/directory/") - onde "/path/to/directory/" deve ser substituído pelo caminho para o diretório de aplicativos, por exemplo "C:/apps/esdi/" .
Se você tiver alguma dúvida ou encontrar algum problema (bugs, recursos desejados), escreva um email ou abra um novo problema.
Cohen, J. (1988). Análise de poder estatístico para as ciências comportamentais (2ª ed.). Hillsdale, NJ: Erlbaum.
Lakens, D. (2013). Tamanhos de efeito de cálculo e relatório para facilitar a ciência cumulativa: um primer prático para testes t e ANOVAs. Frontiers in Psychology, 4. Https://doi.org/10.3389/fpsyg.2013.00863
Lakens, D., Scheel, AM, & Isager, PM (2018). Teste de equivalência para pesquisa psicológica: um tutorial. Avanços em Métodos e Práticas em Ciência Psicológica, 1 (2), 259–269. https://doi.org/10.1177/2515245918770963
Perugini, M., Gallucci, M., & Costantini, G. (2018). Uma cartilha prática para análise de poder para desenhos experimentais simples. International Review of Social Psychology, 31 (1), 20. https://doi.org/10.5334/irsp.181
Cite este software como:
Lukács, G., & Specker, E. (2020). Questões de dispersão: diagnóstico e controle de dados Computador de simulação em estudos de teste de informação ocultos. PLOS ONE, 15 (10), E0240259. https://doi.org/10.1371/journal.pone.0240259