Utilizando simulaciones para los valores de entrada dados, esta aplicación R brillante muestra cómo la eficiencia diagnóstica (medida por las tasas de detección correcta o áreas bajo las curvas) cambia en relación con las diferencias de tamaño de la diferencia de medios estandarizados ( SMD ) entre los casos de condición única (cuando se comparan directamente por la falta de controles).
La aplicación está disponible en línea (para simplemente abrir en cualquier navegador web): https://gasparl.shinyapps.io/esdi/
Sin embargo, también es fácil ejecutarlo desde su PC. Solo necesita ejecutar el siguiente comando en R :
shiny :: runGitHub( " esdi " , " gasparl " )` Para esta última alternativa, si aún no la tiene, debe instalar R y luego instalar el paquete shiny dentro de R eg ingresando install.packages("shiny") en la consola. Luego copie la línea shiny::runGitHub("esdi", "gasparl") por ejemplo, en la consola y presione Entrar. Los componentes necesarios se descargarán automáticamente y la aplicación se abrirá en una nueva ventana.
Finalmente, para usar la aplicación en cualquier momento sin acceso a Internet, puede descargar todo el repositorio (o simplemente App.r ) y ejecutar el código en el archivo App.r. Para esto, deberá instalar todos los paquetes R utilizados en el código (enumerados en las primeras líneas).
Para comprender rápidamente la esencia de la aplicación, consulte la sección de ejemplo a continuación o vea antecedentes para la motivación general. Lo que sigue aquí es una explicación técnica detallada.
La única configuración que influye en la relación clave de diagnóstico SMD es la (relación de) desviaciones estándar (SD) de los valores predictoros para los casos y para los controles , que representan la SD generalmente supuesta para los datos de casos positivos y para los datos de los controles, respectivamente (nuevamente, para obtener más explicaciones, ver las secciones de fondo y ejemplo a continuación). El SDS debe estimarse en función de la SDS típica para casos y controles en el área de investigación dada. Sin embargo, las diferencias de SD tienen relativamente poco impacto en los resultados, y para la mayoría de los casos (donde la SD no se conoce o no se puede estimar fácilmente) se puede suponer que dejar la configuración predeterminada ( 1 para ambas SD) aún dará resultados aproximadamente correctos (a menos que el caso SD / Control SD pueda ser muy pequeño o muy pequeño). En otras palabras, la configuración predeterminada de este software probablemente sea aplicable para la mayoría de los escenarios.
Según las SD dadas, las medias de las muestras se calculan automáticamente para cada una de las SMD especificadas en la otra configuración. Nota: Para ser breve y, sin embargo, evitar la abreviatura, SMD (diferencia de medias estandarizada) se indica como "tamaño de efecto" para las opciones y las etiquetas de la parcela en la interfaz. Los conjuntos de datos se generan para todas las diferentes medias (usando las dos SD constantes) con una distribución normal casi perfecta. La especificación de SMD es bastante sencilla: un valor inicial, un valor final y se debe dar un paso. Por ejemplo, un inicio de 0.2 , un final de 0.6 y un paso de 0.1 definirán los siguientes SMD: 0.2 , 0.3 , 0.4 , 0.5 , 0.6 . El paso más pequeño (o más inicio y finalización distante) significa más puntos de datos para calcular y, por lo tanto, estas configuraciones pueden aumentar sustancialmente el tiempo de cálculo.
Es importante tener en cuenta la diferencia entre (a) SMD entre condiciones únicas ("Caso 1" vs. "Caso 2") y (b) el SMD entre el caso y el control de una sola condición ("Caso" vs. "Control"). The first one (a) is indicative of differences in diagnostic efficiency between two diagnostic methods (eg an old method and a new improved method), while the second one (b) is merely an alternative measurement for diagnostic efficiency within a given method (eg the diagnostic efficiency of the old method), and this latter is always in direct positive correlation with the other diagnostic efficiency measures (so larger "case" vs. "control" SMD always means larger rate of Detección correcta y área más grande debajo de la curva).
El SMD inicial "Caso 1" vs. "Control" representa las eficiencias diagnósticas supuestas del método a mejorar (Método 1). (Nota: es posible pero tiene poco sentido en la práctica incluir cero para el valor de inicio, a menos que para fines de demostración, ya que eso significaría que el Método 1 funcionó a nivel de azar, por lo que es inútil en primer lugar). Los gráficos representan la eficiencia diagnóstica (Método 2) del método (Método 2) ( precisión: "Caso 2" vs. "Control" ) en relación con el "Case 1" Vs. Case 2 "Smd. (Nota: Para mayor claridad, siempre es bueno mantener el valor de inicio del "Caso 1" vs. "Caso 2" SMD en cero, que luego ilustra el punto de partida donde aún no hay diferencia entre los dos métodos). Luego se puede ver cómo los aumentos en el SMD entre el "caso 1" y el "caso 2" conducen a cierta extensión de la precisión mejorada, para cada inicio especificado (como las líneas separadas en la trama): esto es la extensión total de esta extensión de la extensión total de la extensión total de la Aplicación.
Los valores se representan de dos maneras diferentes: como precisión total , y como la precisión obtenida . La precisión obtenida se calcula simplemente como precisión total menos la precisión inicial (método 1). La gráfica combinada contiene ambos tipos, mientras que las subtramas representan estos tipos por separado, y pueden explorarse interactivamente flotando sobre las líneas con el cursor para leer los valores precisos de SMD y precisiones en los puntos dados en la gráfica (consulte la sección de ejemplo a continuación).
Dado que el tamaño de la muestra no es infinito, la distribución normal nunca puede ser realmente perfecta y, por lo tanto, habrá pequeñas desviaciones en los resultados de SMD calculados en comparación con la configuración de SMD dada: por ejemplo, un SMD inicial se puede dar como 0.5 en la configuración, pero los resultados reales pueden ser, por ejemplo, 0.51 . El tamaño de la muestra (número de puntos de datos generados) se puede establecer bajo el Sample size de la etiqueta: el número más grande conduce a un tiempo de cálculo un poco mayor, pero resultados más precisos. Un tamaño de muestra de alrededor de 4000 típicamente dará precisión hasta dos dígitos fraccionados, mientras que ca. 15000 pueden ser precisos hasta tres dígitos fraccionales. Es importante destacar que, independientemente del tamaño de la muestra (y la correspondencia de la configuración y los resultados), la relación de SMD y diagnóstico para los resultados dados siempre es exacta y correcta.
La configuración de la gráfica se relaciona con la representación de los datos, y debe explicarse por sí mismo. Todos los valores para el cálculo de los gráficos están disponibles en la pestaña Tabla en una tabla de datos interactivos.
El análisis de potencia prospectiva ( a priori ) para determinar el tamaño de la muestra requerido es crucial para los experimentos de comportamiento (por ejemplo, Perugini, 2018). Para determinar el mayor efecto de interés requerido para el análisis de energía, la forma ideal es confiar en la justificación objetiva (Lakens, 2013; Lakens et al, 2018). Por ejemplo, para comparar dos métodos de diagnóstico diferentes, uno puede considerar las implicaciones de la vida real de un aumento dado en la tasa de detecciones correctas de una enfermedad en relación con los costos del tamaño de la muestra requerido para mostrar evidencia estadística del aumento dado. Un investigador puede tomar la decisión informada y cuidadosa que vale la pena recopilar, por ejemplo, 120 participantes para detectar un aumento de al menos 8% en precisión de detección: un aumento del 2% o incluso del 0.1% también podría tener un beneficio de la vida real importante, pero debido a los recursos limitados no vale la pena recolectar los tamaños de muestra mucho más grandes necesarios para detectar cambios tan pequeños.
Sin embargo, la implicación práctica no siempre es tan sencilla de evaluar. En un escenario específico en diseño experimental, dos métodos de diagnóstico pueden compararse de manera válida usando casos de condición única, omitiendo los controles (también conocidos como "base" o "condición negativa") con recursos de sobra. Este escenario puede ocurrir en cualquiera de los muchos campos que aplican la clasificación binaria, quizás más característicamente en la medicina. Se puede diagnosticar una enfermedad hipotética con una medida X continua, que generalmente es mayor para las personas con una enfermedad dada (como una pequeña protuberancia o enrojecimiento en reacción a una prueba de pinchazo de la piel; casos positivos), mientras que generalmente es lo mismo para personas sanas (como no o poca reacción a una prueba de pinchazo de piel; casos negativos). Por lo tanto, los casos positivos se pueden detectar con una cierta precisión, pero no perfectamente, porque algunas de las mediciones están en cierta medida defectuosas y también dan valores erróneamente bajos para casos positivos. Si alguien propuso una mejora en el procedimiento para lograr valores más altos en la medida X , sería posible comparar directamente los dos métodos solo en casos positivos: dado que la medida siempre será constante (baja) en casos negativos (personas sanas), los valores más altos para casos positivos significa que el procedimiento también tendrá una mejor eficiencia diagnóstica.
El problema aquí es que el tamaño del efecto para el cálculo potencial de potencia es entre dos condiciones positivas, que no tienen implicaciones directas para las consecuencias prácticas en el diagnóstico. El presente software ayuda al proporcionar estimaciones para los valores de eficiencia diagnóstica (tasas de detección y áreas correctas bajo las curvas) para los tamaños de efecto dados entre las condiciones positivas solo.
Este software en realidad se inspiró en estudios de prueba de información oculta (CIT): el CIT puede revelar que una persona reconoce un elemento de sonda relevante (por ejemplo, una arma homicida específica utilizada en un crimen reciente), entre otros elementos irrelevantes (por ejemplo, otras armas plausibles), basada en diferentes, por ejemplo, que responde más lentamente a la investigación en comparación con los ítems irrelevantes. Dado que las personas inocentes no reconocen la sonda como relevante, sus respuestas no diferirán entre la sonda y los elementos irrelevantes. Por lo tanto, según las diferencias más grandes de sonda-minus-irrelevantes ( PI ), las personas culpables pueden distinguirse de las inocentes. De manera crucial, dado que el PI siempre es alrededor de cero para inocentes, muchos estudios comparan diferentes versiones de la CIT mediante el uso solo de grupos de culpabilidad, con el entendimiento de que el grupo PI más grande significa para una versión dada significa que la eficiencia diagnóstica también será mejor utilizando esa versión (es decir, más culpables se puede distinguir correctamente de las inocentes). Sin embargo, la diferencia en la media aritmética entre dos grupos de culpabilidad (o el SMD relacionado) realmente no tiene ninguna implicación práctica sensata y, por lo tanto, no puede usarse para una decisión educada sobre el tamaño de la muestra. De hecho, 13 de los 24 estudios recolectados en un metaanálisis reciente (Lukács y Specker, 2020) utilizaron una comparación de condición única, ninguno informó un cálculo de potencia previa para los tamaños de muestra, e incluso la interpretación de los tamaños de los efectos se basó en los famosos de Cohen, pero al final arbitrarios, sin un significado práctico directo (Cohen, 1988; Lakens et al, 2018).
Ahora, este metanálisis también informó SD promedio (basado en 12 experimentos) para casos (grupos de culpabilidad) y controles (grupos inocentes), 33.6 y 23.5 , respectivamente, por lo que estos pueden usarse en la aplicación ESDI como valores de entrada para el caso SD y control SD . Sin embargo, el uso del valor predeterminado de 1 para ambos SD en realidad ofrece resultados muy similares: en general, saber y dar estimaciones de SD precisas no es vital (a menos que la relación SD / Control SD del caso pueda ser muy grande o muy pequeña).
Dando los 33.6 y 23.5 para el caso SD y el control SD , 4000 para el tamaño de la muestra y dejando todas las demás configuraciones sin cambios, la trama combinada principal se verá así:
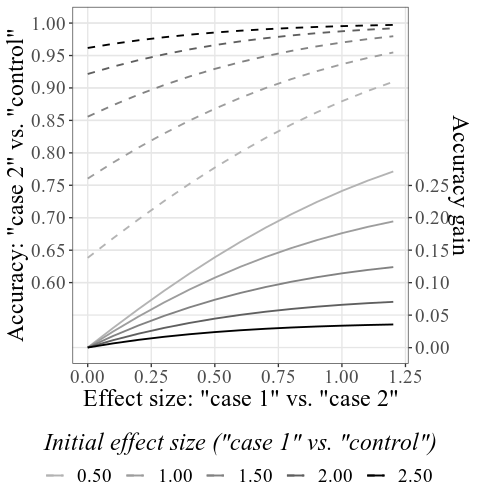
Tenga en cuenta que, como se explica en detalle en la sección Cómo usar arriba, las precisiones iniciales se calculan en función de las SMD iniciales dadas (ver etiqueta inferior; en Configuración de la trama, esta etiqueta se puede cambiar para mostrar las precisiones en lugar de las SMD). Los SMD resultantes pueden diferir ligeramente de los SMD dados en la configuración, debido al proceso de simulación (nuevamente, consulte cómo usar para detalles técnicos).
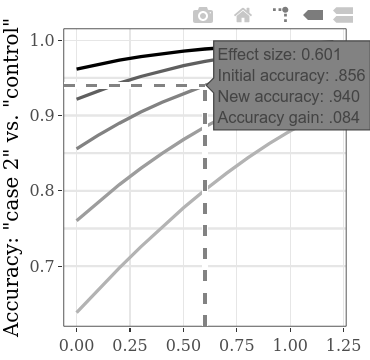
El aumento de la precisión total o la precisión ganada análoga, en la función del aumento en la condición (culpable 1 vs. culpable 2) SMD, se puede explorar por separado en las subtramas interactivas. Por ejemplo, flotando sobre la línea como se muestra a continuación, la etiqueta que aparece muestra que si encontramos un tamaño de efecto (SMD) de 0.601 entre los resultados de dos grupos de culpabilidad, dada una precisión inicial de .856 (tasa de personas correctamente detectadas, tanto culpables como inocentes), los aumentos de precisión por .084 (por lo tanto, con una nueva precisión de .940). Si suponemos que la precisión inicial (es decir, la precisión que usa el método con la eficiencia diagnóstica inferior) de este tipo de CIT es generalmente alrededor de .856, podemos usar los valores SMD en esta línea para el cálculo de potencia. Por ejemplo, con el SMD 0.6, para una potencia de .9, el tamaño de muestra requerido por grupo es 60 (para una prueba t no apareada con alfa = .05). Por lo tanto, para detectar estadísticamente un aumento de al menos .084 en precisión de detección, se debe recolectar un total de 120 personas para las dos condiciones de culpabilidad.
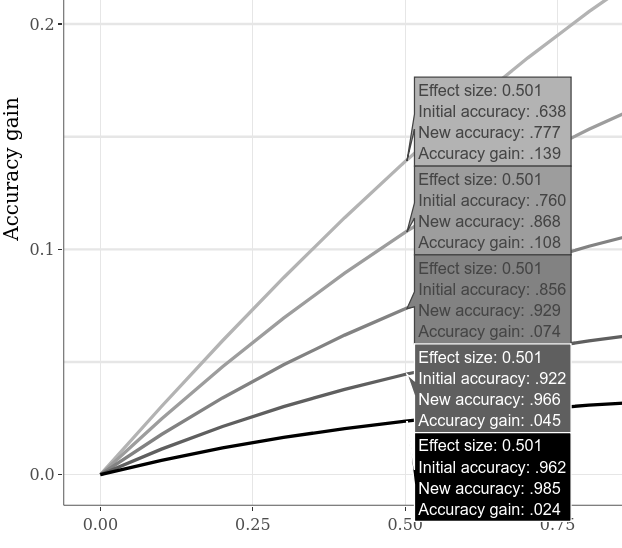
Las precisiones iniciales alternativas se pueden comparar, por ejemplo, cambiando a la gran pestaña de subtramas interactivas , haciendo clic en la opción "Comparar datos sobre el despilfarro" en la gráfica inferior y mover el cursor horizontalmente a lo largo de la gráfica. El siguiente ejemplo muestra varias ganancias de precisión cuando el SMD "Caso 1" vs. "Caso 2" es 0.5. Como ya era evidente en los gráficos de ejemplo anteriores, la precisión inicial más baja siempre permite una mayor ganancia de precisión.
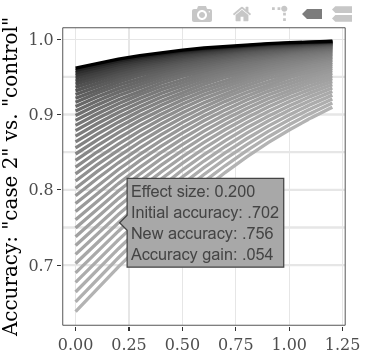
Para explorar más valores iniciales iniciales al mismo tiempo, la configuración de paso para el SMD "CASE 1" versus "Control" se puede reducir, lo que lleva a más líneas en la gráfica (y a un tiempo de cálculo un poco mayor). (El paso para el "caso 1" vs. "Caso 2" SMD dará como resultado análogos en puntos de datos más horizontales).
Por defecto, las tasas simples de detección correcta (número de todos los sujetos clasificados correctamente divididos por el número de todos los sujetos) se muestran para la medición de "precisión", ya que este es probablemente el indicador más directo de la eficiencia diagnóstica. Se puede cambiar a área debajo de la curva debajo de la pestaña "Parcela" en el panel izquierdo. En la misma pestaña, las etiquetas de la trama también se pueden personalizar.
La funcionalidad básica del software se puede verificar utilizando el paquete shinytest para ejecutar un traje de prueba automatizado (por ejemplo, después de hacer contribuciones). Simplemente ejecute shinytest::recordTest("/path/to/directory/") - Donde "/path/to/directory/" debe reemplazarse con la ruta al directorio de aplicaciones, por ejemplo "C:/apps/esdi/" .
Si tiene alguna pregunta o encuentra algún problema (errores, funciones deseadas), escriba un correo electrónico o abra un nuevo problema.
Cohen, J. (1988). Análisis de poder estadístico para las ciencias del comportamiento (2ª ed.). Hillsdale, NJ: Erlbaum.
Lakens, D. (2013). Cálculo de tamaños de efecto de cálculo e informes para facilitar la ciencia acumulativa: un imprimador práctico para pruebas t y ANOVA. Frontiers in Psychology, 4. Https://doi.org/10.3389/fpsyg.2013.00863
Lakens, D., Scheel, AM e Isager, PM (2018). Pruebas de equivalencia para la investigación psicológica: un tutorial. Avances en métodos y prácticas en ciencias psicológicas, 1 (2), 259–269. https://doi.org/10.1177/2515245918770963
Perugini, M., Gallucci, M. y Costantini, G. (2018). Un manual práctico para el análisis de potencia para diseños experimentales simples. International Review of Social Psychology, 31 (1), 20. https://doi.org/10.5334/irsp.181
Cita este software como:
Lukács, G. y Specker, E. (2020). Asuntos de dispersión: diagnóstico y control de datos Simulación informática en estudios de prueba de información ocultos. PLoS One, 15 (10), E0240259. https://doi.org/10.1371/journal.pone.0240259