Menggunakan simulasi untuk nilai input yang diberikan, aplikasi R mengkilap ini menunjukkan bagaimana perubahan efisiensi diagnostik (yang diukur dengan laju deteksi yang benar atau area di bawah kurva) berubah dalam kaitannya dengan perbedaan ukuran efek rata-rata standar ( SMD ) antara kasus kondisi tunggal (ketika ini secara langsung dibandingkan dengan kurangnya kontrol).
Aplikasi ini tersedia secara online (hanya akan dibuka di browser web apa pun): https://gasparl.shinyapps.io/esdi/
Namun, juga mudah untuk menjalankannya dari PC Anda. Anda hanya perlu menjalankan perintah berikut di r :
shiny :: runGitHub( " esdi " , " gasparl " )` Untuk alternatif terakhir ini, jika Anda belum memilikinya, Anda perlu menginstal R dan kemudian menginstal paket shiny dalam R EG dengan memasukkan install.packages("shiny") . Kemudian salin garis shiny::runGitHub("esdi", "gasparl") misalnya di konsol dan tekan Enter. Komponen yang diperlukan akan diunduh secara otomatis dan aplikasi akan terbuka di jendela baru.
Akhirnya, untuk menggunakan aplikasi kapan saja tanpa akses internet, Anda dapat mengunduh seluruh repositori (atau hanya app.r ) dan menjalankan kode di file app.r. Untuk ini, Anda perlu menginstal semua paket R yang digunakan dalam kode (tercantum dalam baris pertama).
Untuk dengan cepat memahami esensi aplikasi, lihat bagian contoh di bawah ini, atau lihat latar belakang untuk motivasi umum. Berikut ini di sini adalah penjelasan teknis terperinci.
Satu-satunya pengaturan yang mempengaruhi hubungan utama SMD-diagnostik adalah (rasio) standar deviasi (SD) dari nilai prediktor untuk kasus dan untuk kontrol , yang mewakili SD yang umumnya diasumsikan untuk data dari kasus positif dan untuk data dari kontrol, masing-masing, untuk penjelasan lebih lanjut, lihat bagian latar belakang dan contoh bagian di bawah). SDS harus diperkirakan berdasarkan SDS khas untuk kasus dan kontrol di bidang penelitian yang diberikan. Namun, perbedaan SD memiliki dampak yang relatif sedikit pada hasil, dan untuk kebanyakan kasus (di mana SD tidak diketahui atau tidak dapat dengan mudah diperkirakan) dapat diasumsikan bahwa meninggalkan pengaturan default ( 1 untuk kedua SD) masih akan memberikan hasil yang kira -kira benar (kecuali SD / kontrol SD mungkin sangat besar atau sangat kecil). Dengan kata lain, pengaturan default perangkat lunak ini mungkin berlaku untuk sebagian besar skenario.
Berdasarkan SDS yang diberikan, sarana sampel secara otomatis dihitung untuk masing -masing SMD yang ditentukan di bawah pengaturan lainnya. CATATAN: Agar singkat namun menghindari singkatan, SMD (perbedaan rata -rata standar) diindikasikan sebagai "ukuran efek" untuk opsi dan label plot pada antarmuka. Dataset dihasilkan untuk semua cara yang berbeda (menggunakan dua SDS konstan) dengan distribusi normal yang hampir sempurna. Spesifikasi SMD cukup mudah: nilai awal, nilai akhir, dan langkah harus diberikan. Misalnya, awal 0.2 , ujung 0.6 , dan satu langkah 0.1 akan menentukan SMD berikut: 0.2 , 0.3 , 0.4 , 0.5 , 0.6 . Langkah yang lebih kecil (atau start dan akhir yang lebih jauh) berarti lebih banyak titik data untuk menghitung, dan oleh karena itu pengaturan ini secara substansial dapat meningkatkan waktu perhitungan.
Penting untuk diingat perbedaan antara (a) SMD antara kondisi tunggal ("Kasus 1" vs "Kasus 2") dan (b) SMD antara kasus dan kontrol kondisi tunggal ("case" vs "kontrol"). Yang pertama (a) adalah indikasi perbedaan dalam efisiensi diagnostik antara dua metode diagnostik (misalnya metode lama dan metode baru yang lebih baik), sedangkan yang kedua (b) hanyalah pengukuran alternatif untuk efisiensi diagnostik dalam metode yang lebih besar (mis. Efisiensi diagnostik "Kasus yang lebih besar), dan efisiensi yang lebih besar dalam korelasi yang lebih besar dengan Kontrol yang lebih besar dengan Kontrol Lainnya. deteksi yang benar dan area yang lebih besar di bawah kurva).
"Kasus 1" vs awal "kontrol" SMD mewakili efisiensi diagnostik yang diasumsikan dari metode yang akan ditingkatkan (Metode 1). (Catatan: Dimungkinkan tetapi tidak masuk akal dalam praktiknya untuk memasukkan nol untuk nilai awal, kecuali untuk tujuan demonstrasi, karena itu berarti bahwa metode 1 berkinerja pada level peluang, jadi tidak berguna di tempat pertama.) Plot menggambarkan peningkatan metode diagnostik (Metode 2) ( akurasi: "Kasus 2" vs. "Kontrol" ) dalam kaitannya dengan "kasus 1" vs. "vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. vs. Vs. (Catatan: Untuk kejelasan, selalu baik untuk menjaga nilai awal dari "kasus 1" vs "case 2" SMD pada nol, yang kemudian menggambarkan titik awal di mana belum ada perbedaan sama sekali antara dua metode.) Kemudian dapat dilihat bagaimana peningkatan smd antara inisial ini.
Nilai -nilai digambarkan dalam dua cara berbeda: sebagai akurasi total , dan sebagai akurasi yang diperoleh . Akurasi yang diperoleh dihitung hanya sebagai akurasi total dikurangi akurasi awal (metode 1). Plot gabungan berisi kedua jenis, sedangkan subplot menggambarkan tipe -tipe ini secara terpisah, dan dapat dieksplorasi secara interaktif dengan melayang di atas garis dengan kursor untuk membaca nilai -nilai yang tepat dari SMD dan akurasi pada titik -titik yang diberikan pada plot (lihat bagian contoh di bawah).
Karena ukuran sampel tidak terbatas, distribusi normal tidak akan pernah benar -benar sempurna, dan oleh karena itu akan ada penyimpangan kecil dalam hasil SMD yang dihitung dibandingkan dengan pengaturan SMD yang diberikan: misalnya, satu SMD awal dapat diberikan sebagai 0.5 dalam pengaturan, tetapi hasil sebenarnya mungkin, misalnya, 0.51 . Ukuran sampel (jumlah titik data yang dihasilkan) dapat ditetapkan di bawah Sample size label: jumlah yang lebih besar menyebabkan sedikit peningkatan waktu perhitungan, tetapi hasil yang lebih tepat. Ukuran sampel sekitar 4000 biasanya akan memberikan presisi hingga dua digit fraksional, sedangkan ca. 15000 mungkin tepat hingga tiga digit fraksional. Yang penting, terlepas dari ukuran sampel (dan korespondensi pengaturan dan hasil), hubungan SMD dan diagnostik untuk hasil yang diberikan selalu tepat dan benar.
Pengaturan plot terkait dengan penggambaran data, dan harus jelas. Semua nilai untuk perhitungan plot tersedia di bawah tab Tabel dalam tabel data interaktif.
Analisis daya prospektif ( a priori ) untuk menentukan ukuran sampel yang diperlukan sangat penting untuk percobaan perilaku (misalnya, Perugini, 2018). Untuk menentukan efek terkecil yang diperlukan untuk analisis daya, cara yang ideal adalah dengan mengandalkan pembenaran objektif (Lakens, 2013; Lakens et al, 2018). Sebagai contoh, untuk membandingkan dua metode diagnostik yang berbeda, orang dapat mempertimbangkan implikasi kehidupan nyata dari peningkatan yang diberikan dalam tingkat deteksi penyakit yang benar sehubungan dengan biaya ukuran sampel yang diperlukan untuk menunjukkan bukti statistik untuk peningkatan yang diberikan. Seorang peneliti dapat membuat keputusan yang diinformasikan dan cermat yang layak dikumpulkan, katakanlah, 120 peserta untuk mendeteksi peningkatan setidaknya 8% dalam akurasi deteksi: peningkatan 2% atau bahkan 0,1% juga dapat memiliki manfaat kehidupan nyata yang penting, tetapi karena sumber daya yang terbatas tidak layak mengumpulkan ukuran sampel yang jauh lebih besar yang diperlukan untuk mendeteksi perubahan yang lebih kecil seperti itu.
Namun, implikasi praktis tidak selalu begitu mudah untuk dinilai. Dalam satu skenario spesifik dalam desain eksperimental, dua metode diagnostik dapat secara sah dibandingkan dengan menggunakan kasus kondisi tunggal, menghilangkan kontrol (alias "baseline" atau "kondisi negatif") dengan sumber daya cadangan. Skenario ini dapat terjadi di salah satu dari banyak bidang yang menerapkan klasifikasi biner, mungkin yang paling khas dalam kedokteran. Penyakit hipotetis dapat didiagnosis dengan ukuran X kontinen, yang biasanya lebih tinggi untuk orang dengan penyakit tertentu (seperti benjolan kecil atau kemerahan sebagai reaksi terhadap tes tusukan kulit; kasus positif), sementara itu umumnya sama untuk orang sehat (seperti tidak ada atau sedikit reaksi terhadap tes tusukan kulit; kasus negatif). Dengan demikian kasus positif dapat dideteksi dengan akurasi tertentu - tetapi tidak sempurna, karena beberapa pengukuran sampai batas tertentu salah dan memberikan nilai yang keliru untuk kasus positif juga. Jika seseorang mengusulkan peningkatan prosedur untuk mencapai nilai yang lebih tinggi dalam ukuran X , dimungkinkan untuk secara langsung membandingkan kedua metode hanya pada kasus positif: karena ukuran akan selalu konstan (rendah) dalam kasus negatif (orang sehat), nilai yang lebih tinggi untuk kasus positif berarti bahwa prosedur juga akan memiliki efisiensi diagnostik yang lebih baik.
Masalahnya di sini adalah bahwa ukuran efek untuk perhitungan daya potensial adalah antara dua kondisi positif, yang tidak memiliki implikasi langsung untuk konsekuensi praktis dalam diagnostik. Perangkat lunak ini membantu dengan memberikan estimasi untuk nilai efisiensi diagnostik (tingkat deteksi yang benar dan area di bawah kurva) untuk ukuran efek yang diberikan antara kondisi positif saja.
Perangkat lunak ini sebenarnya terinspirasi oleh studi Tes Informasi Tersembunyi (CIT): CIT dapat mengungkapkan bahwa seseorang mengakui item penyelidikan yang relevan (misalnya senjata pembunuhan khusus yang digunakan dalam kejahatan baru -baru ini) di antara barang -barang yang tidak relevan (misalnya senjata masuk akal lainnya), berdasarkan pada yang berbeda, EG lebih lambat menanggapi penyelidikan dibandingkan dengan barang -barang yang tidak relevan). Karena orang yang tidak bersalah tidak mengakui penyelidikan sebagai relevan, tanggapan mereka rata -rata tidak akan berbeda antara probe dan item yang tidak relevan. Oleh karena itu, berdasarkan perbedaan probe-minus-tidak relevan ( PI ) yang lebih besar, orang-orang yang bersalah dapat dibedakan dari yang tidak bersalah. Yang terpenting, karena PI selalu sekitar nol untuk orang tak berdosa, banyak penelitian membandingkan versi yang berbeda dari CIT dengan hanya menggunakan kelompok bersalah, dengan pemahaman bahwa kelompok PI yang lebih besar berarti untuk versi yang diberikan berarti bahwa efisiensi diagnostik juga akan lebih baik menggunakan versi itu (yaitu lebih banyak orang yang bersalah dapat dibedakan dengan benar dari yang tidak bersalah). Namun, perbedaan rata -rata aritmatika antara dua kelompok bersalah (atau SMD terkait) tidak benar -benar memiliki implikasi praktis yang masuk akal, dan oleh karena itu tidak dapat digunakan untuk keputusan yang berpendidikan tentang ukuran sampel. Memang, 13 dari 24 studi yang dikumpulkan dalam meta-analisis baru-baru ini (Lukács & Specker, 2020) menggunakan perbandingan kondisi tunggal, tidak ada yang melaporkan perhitungan daya sebelumnya untuk ukuran sampel, dan bahkan interpretasi ukuran efek didasarkan pada Cohen yang terkenal tetapi pada akhirnya Benchmarks.
Sekarang, meta-analisis ini juga melaporkan SDS rata-rata (berdasarkan 12 percobaan) untuk kasus (kelompok bersalah) dan kontrol (kelompok yang tidak bersalah), 33.6 dan 23.5 , masing-masing-sehingga ini dapat digunakan dalam aplikasi ESDI sebagai nilai input untuk SD kasus dan kontrol SD . Namun, menggunakan nilai default 1 untuk kedua SDS sebenarnya memberikan hasil yang sangat mirip: secara umum, mengetahui dan memberikan estimasi SD yang tepat tidak vital (kecuali case SD / kontrol rasio SD mungkin sangat besar atau sangat kecil).
Memberikan 33.6 dan 23.5 untuk kasus SD dan kontrol SD , 4000 untuk ukuran sampel , dan meninggalkan semua pengaturan lainnya tidak berubah, plot gabungan utama akan terlihat seperti ini:
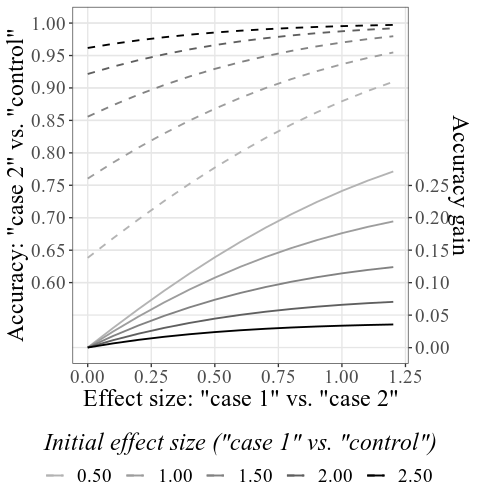
Perhatikan bahwa - seperti yang dijelaskan secara rinci di bawah bagian Cara Penggunaan di atas - Akurasi awal dihitung berdasarkan SMD awal yang diberikan (lihat label bawah; di bawah pengaturan plot label ini dapat diubah untuk menampilkan akurasi alih -alih SMD). SMD yang dihasilkan mungkin sedikit berbeda dari SMD yang diberikan dalam pengaturan, karena proses simulasi (sekali lagi, lihat cara menggunakan untuk detail teknis).
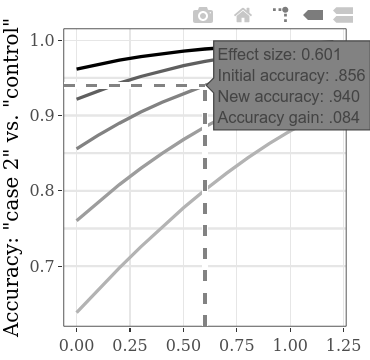
Peningkatan akurasi total atau akurasi yang diperoleh analog, dalam fungsi peningkatan antar-kondisi (bersalah 1 vs bersalah 2) SMD, dapat dieksplorasi secara terpisah pada subplot interaktif. Misalnya, melayang di atas garis seperti yang ditunjukkan di bawah ini, label yang muncul menunjukkan bahwa jika kita menemukan ukuran efek (SMD) 0,601 antara hasil dua kelompok bersalah, diberi akurasi awal 0,856 (tingkat orang yang terdeteksi dengan benar, baik yang bersalah maupun tidak bersalah), akurasi yang meningkat dengan .084 (oleh karena itu menghasilkan akurasi baru .9. Jika kita mengasumsikan bahwa akurasi awal (yaitu, akurasi menggunakan metode dengan efisiensi diagnostik inferior) dari jenis CIT ini memang sekitar 0,856, kita dapat menggunakan nilai SMD pada saluran ini untuk perhitungan daya. Misalnya, dengan SMD 0,6, untuk kekuatan 0,9, ukuran sampel yang diperlukan per grup adalah 60 (untuk uji-t tidak berpasangan dengan alpha = 0,05). Oleh karena itu, untuk secara statistik mendeteksi peningkatan setidaknya 0,084 dalam akurasi deteksi, total 120 orang perlu dikumpulkan untuk dua kondisi bersalah.
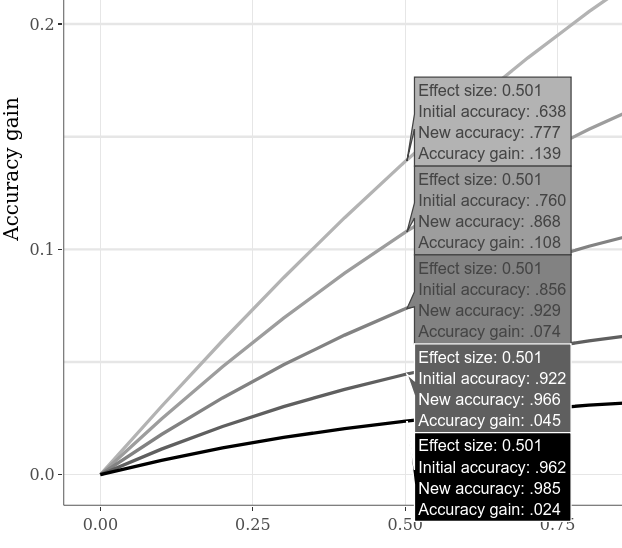
Akurasi awal alternatif dapat dibandingkan dengan, misalnya, beralih ke tab Subplot Interaktif Besar , mengklik opsi "Bandingkan Data tentang Hover" pada plot yang lebih rendah, dan menggerakkan kursor secara horizontal di sepanjang plot. Contoh di bawah ini menunjukkan berbagai keuntungan akurasi ketika "case 1" vs "case 2" SMD adalah 0,5. Karena sudah jelas pada plot contoh sebelumnya, akurasi awal yang lebih rendah selalu memungkinkan kenaikan akurasi yang lebih besar.
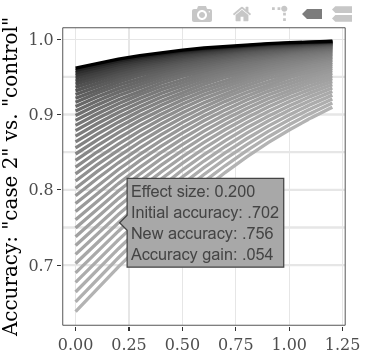
Untuk mengeksplorasi lebih banyak nilai awal awal pada saat yang sama, pengaturan langkah untuk "case 1" vs "kontrol" SMD dapat diturunkan, mengarah ke lebih banyak garis pada plot (dan untuk sedikit meningkatkan waktu perhitungan). (Langkah untuk "Kasus 1" vs "Kasus 2" SMD akan secara analog menghasilkan lebih banyak titik data horizontal.)
Secara default, tingkat deteksi yang benar (jumlah semua subjek yang diklasifikasikan dengan benar dibagi dengan jumlah semua subjek) ditampilkan untuk pengukuran "akurasi", karena ini mungkin merupakan indikator efisiensi diagnostik yang paling mudah. Ini dapat diubah ke area di bawah kurva di bawah tab "Plot" di panel kiri. Di bawah tab yang sama, label plot juga dapat disesuaikan.
Fungsi dasar perangkat lunak dapat diverifikasi menggunakan paket shinytest untuk menjalankan gugatan uji otomatis (misalnya setelah memberikan kontribusi). Cukup jalankan shinytest::recordTest("/path/to/directory/") - di mana "/path/to/directory/" harus diganti dengan jalur ke direktori aplikasi, misalnya "C:/apps/esdi/" .
Jika Anda memiliki pertanyaan atau menemukan masalah (bug, fitur yang diinginkan), tulis email atau buka masalah baru.
Cohen, J. (1988). Analisis kekuatan statistik untuk ilmu perilaku (edisi ke -2). Hillsdale, NJ: Erlbaum.
Lakens, D. (2013). Menghitung dan pelaporan efek efek untuk memfasilitasi ilmu kumulatif: primer praktis untuk uji-t dan ANOVA. Frontiers in Psychology, 4. Https://doi.org/10.3389/fpsyg.2013.00863
Lakens, D., Scheel, AM, & Isager, PM (2018). Pengujian Kesetaraan untuk Penelitian Psikologis: Tutorial. Kemajuan dalam Metode dan Praktik dalam Ilmu Psikologis, 1 (2), 259-269. https://doi.org/10.1177/2515245918770963
Perugini, M., Gallucci, M., & Costantini, G. (2018). Primer praktis untuk analisis daya untuk desain eksperimental sederhana. Tinjauan Internasional Psikologi Sosial, 31 (1), 20. https://doi.org/10.5334/irsp.181
Mengutip perangkat lunak ini sebagai:
Lukács, G., & Specker, E. (2020). PENGETAHUAN DISPERSI: Diagnostik dan Kontrol Data Simulasi Komputer dalam Studi Uji Informasi Tersembunyi. PLoS One, 15 (10), E0240259. https://doi.org/10.1371/journal.pone.0240259