باستخدام المحاكاة لقيم الإدخال المحددة ، يوضح هذا التطبيق R اللامع كيف يتغير كفاءة التشخيص (كما تم قياسه بمعدلات الكشف الصحيح أو المناطق بموجب المنحنيات) فيما يتعلق بالاختلاف في حجم الفرق الموحد ( SMD ) بين حالات الشرط الواحد (عند مقارنتها بشكل مباشر لعدم وجود عناصر التحكم).
التطبيق متاح عبر الإنترنت (ليتم فتحه ببساطة في أي متصفح ويب): https://gasparl.shinyapps.io/esdi/
ومع ذلك ، من السهل أيضًا تشغيله من جهاز الكمبيوتر الخاص بك. تحتاج فقط إلى تشغيل الأمر التالي في R :
shiny :: runGitHub( " esdi " , " gasparl " )` لهذا البديل الأخير ، إذا لم يكن لديك بالفعل ، فأنت بحاجة إلى تثبيت R ثم تثبيت الحزمة shiny داخل R EG عن طريق إدخال install.packages("shiny") في وحدة التحكم. ثم انسخ الخط shiny::runGitHub("esdi", "gasparl") على سبيل المثال في وحدة التحكم واضغط على Enter. سيتم تنزيل المكونات اللازمة تلقائيًا وسيتم فتح التطبيق في نافذة جديدة.
أخيرًا ، لاستخدام التطبيق في أي وقت بدون الوصول إلى الإنترنت ، يمكنك تنزيل المستودع بالكامل (أو فقط App.r ) وتشغيل الرمز في ملف App.R. لهذا ، ستحتاج إلى تثبيت جميع حزم R المستخدمة في الكود (المدرجة في الأسطر الأولى).
لفهم جوهر التطبيق بسرعة ، راجع القسم المثال أدناه ، أو رؤية خلفية الدافع العام. ما يلي هو تفسير تقني مفصل.
الإعدادات الوحيدة التي تؤثر على علاقة SMD-Diaghinostics الرئيسية هي (نسبة) الانحرافات المعيارية (SDS) لقيم التنبؤ للحالات وللتحكم ، والتي تمثل SD المفترض عمومًا للبيانات من الحالات الإيجابية وللبيانات من عناصر التحكم ، على التوالي (مرة أخرى ، لمزيد من التفسير ، راجع الأقسام والمثال أدناه). يجب تقدير SDS بناءً على SDS النموذجية للحالات والضوابط في مجال البحث المحدد. ومع ذلك ، فإن اختلافات SD لها تأثير ضئيل نسبيًا على النتائج ، وبالنسبة لمعظم الحالات (عندما لا تكون SD معروفة أو لا يمكن تقديرها بسهولة) ، يمكن افتراض أن ترك الإعدادات الافتراضية ( 1 لكلا SDs) سيظلان يعطي نتائج صحيحة تقريبًا (ما لم تكن SD / Control SD كبيرة جدًا أو صغيرة جدًا). بمعنى آخر ، من المحتمل أن تكون الإعدادات الافتراضية لهذا البرنامج قابلة للتطبيق لمعظم السيناريوهات.
استنادًا إلى SDS المحددة ، يتم حساب وسائل العينات تلقائيًا لكل من SMDs المحددة تحت الإعدادات الأخرى. ملاحظة: لكي تكون موجزًا وتجنب الاختصار ، يشار إلى SMD (الفرق المتوسط الموحد) على أنه "حجم التأثير" للخيار والمؤامرة على الواجهة. يتم إنشاء مجموعات البيانات لجميع الوسائل المختلفة (باستخدام اثنين من SDS الثابتة) مع التوزيع الطبيعي شبه المثالي. مواصفات SMDs واضحة إلى حد ما: يجب إعطاء قيمة البداية ، القيمة النهائية ، خطوة. على سبيل المثال ، ستحدد بداية 0.2 ، ونهاية 0.6 ، وخطوة 0.1 SMDs التالية: 0.2 ، 0.3 ، 0.4 ، 0.5 ، 0.6 . تعني الخطوة الأصغر (أو بداية ونهاية أكثر) المزيد من نقاط البيانات لحسابها ، وبالتالي يمكن أن تزيد هذه الإعدادات بشكل كبير من وقت الحساب.
من المهم أن تضع في اعتبارك الفرق بين (أ) SMD بين الشروط الواحدة ("الحالة 1" "مقابل" الحالة 2 ") و (ب) SMD بين الحالة والتحكم في حالة واحدة (" الحالة "مقابل" التحكم "). الأول (أ) يدل على الاختلافات في الكفاءة التشخيصية بين طريقتين تشخيصيين (على سبيل المثال طريقة قديمة وطريقة جديدة محسّنة) ، في حين أن الثانية (ب) هي مجرد قياس بديل للتصحيح التشخيصي المعدل (مثل الكفاءة التشخيصية ذات المعدل الكبير ". من الكشف الصحيح والمساحة الأكبر تحت المنحنى).
تمثل الحالة الأولية "CASE 1" مقابل "التحكم" SMD الكفاءة التشخيصية المفترضة للطريقة التي سيتم تحسينها (الطريقة 1). (ملاحظة: من الممكن ، ولكن ليس من المنطقي في الممارسة العملية أن تضم صفرًا لقيمة البدء ، ما لم يكن لأغراض التوضيح ، لأن هذا يعني أن الطريقة 1 تؤدي على مستوى الفرصة ، لذلك فهي غير مجدية في المقام الأول.) تصور المؤامرات كفاءة التشخيص المحسّنة في الطريقة 2 "SMD 2" SMD . (ملاحظة: من أجل الوضوح ، من الجيد دائمًا الحفاظ على قيمة بداية "الحالة 1" "مقابل" الحالة 2 "SMD عند الصفر ، والتي توضح بعد ذلك نقطة البداية التي لا يوجد فيها فرق على الإطلاق بين الطريقتين.) ثم يمكن رؤية كيفية زيادة هذه الخطورة في SMD بين هذه الحالة.
يتم تصوير القيم بطريقتين مختلفتين: كدقة تامة ، وكما اكتسبت الدقة . يتم حساب الدقة المكتسبة ببساطة كدقة كاملة ناقص الأولي (الطريقة 1) الدقة. تحتوي المؤامرة المدمجة على كلا النوعين ، في حين أن المخططات الفرعية تصور هذه الأنواع بشكل منفصل ، ويمكن استكشافها بشكل تفاعلي عن طريق التحوم على الخطوط مع المؤشر لقراءة القيم الدقيقة لل SMDs ودقة في النقاط المحددة على المؤامرة (انظر القسم المثال أدناه).
نظرًا لأن حجم العينة ليس غير محدود ، فإن التوزيع الطبيعي لا يمكن أن يكون أبدًا مثاليًا حقًا ، وبالتالي سيكون هناك انحرافات صغيرة في نتائج SMD المحسوبة مقارنةً بإعدادات SMD المعطاة: على سبيل المثال ، قد يتم إعطاء SMD أولي كـ 0.5 في الإعدادات ، ولكن قد تكون النتائج الفعلية ، على سبيل المثال ، 0.51 . يمكن ضبط حجم العينة (عدد نقاط بيانات البيانات التي تم إنشاؤها) تحت Sample size العينة: يؤدي عدد أكبر إلى زيادة وقت الحساب إلى حد ما ، ولكن نتائج أكثر دقة. عادةً ما يعطي حجم عينة يبلغ حوالي 4000 دقة ما يصل إلى رقمين كسريين ، بينما CA. قد يكون 15000 دقيقًا حتى ثلاثة أرقام كسرية. الأهم من ذلك ، بغض النظر عن حجم العينة (ومراسلة الإعدادات والنتائج) ، فإن علاقة SMD والتشخيصات للنتائج المحددة دائمًا دقيقة وصحيحة.
تتعلق إعدادات المؤامرة بتصوير البيانات ، ويجب أن تكون غير متوسطة. تتوفر جميع القيم الخاصة بحساب المخططات ضمن علامة التبويب الجدول في جدول بيانات تفاعلي.
تحليل الطاقة المحتملين ( مسبق ) لتحديد حجم العينة المطلوب أمر بالغ الأهمية للتجارب السلوكية (على سبيل المثال ، Perugini ، 2018). لتحديد أصغر تأثير الاهتمام المطلوب لتحليل الطاقة ، فإن الطريقة المثالية هي الاعتماد على التبرير الموضوعي (Lakens ، 2013 ؛ Lakens et al ، 2018). على سبيل المثال ، لمقارنة طريقتين تشخيصيين مختلفين ، قد ينظر المرء في آثار الحياة الحقيقية لزيادة معينة في معدل الاكتشافات الصحيحة للمرض فيما يتعلق بتكاليف حجم العينة المطلوبة لإظهار الأدلة الإحصائية لتلك الزيادة المحددة. قد يتخذ الباحث قرارًا مستنيرًا ودقيقًا بأنه من المفيد جمع 120 مشاركًا للكشف عن زيادة بنسبة 8 ٪ على الأقل في دقة الكشف: قد يكون للزيادة بنسبة 2 ٪ أو حتى 0.1 ٪ أيضًا فائدة مهمة مهمة ، ولكن بسبب الموارد المحدودة ، لا يستحق جمع أحجام العينات الأكبر حجمًا المطلوبة للكشف عن مثل هذه التغييرات الأصغر.
ومع ذلك ، فإن الآثار العملية ليست دائما واضحة جدا للتقييم. في سيناريو واحد محدد في التصميم التجريبي ، قد تتم مقارنة طريقتين تشخيصتين بشكل صحيح باستخدام حالات شرط أحادية ، وحذف عناصر التحكم (المعروفة أيضًا باسم "خط الأساس" أو "الحالة السلبية") لتجنيب الموارد. يمكن أن يحدث هذا السيناريو في أي من الحقول العديدة التي تطبق تصنيفًا ثنائيًا ، وربما الأكثر تميزًا في الطب. قد يتم تشخيص مرض افتراضية مع مقياس مستمر X ، والذي عادةً ما يكون أعلى للأشخاص الذين يعانون من مرض معين (مثل عثرة صغيرة أو احمرار في رد الفعل لاختبار وخز الجلد ؛ الحالات الإيجابية) ، في حين أنه هو نفسه بشكل عام للأشخاص الأصحاء (مثل عدم وجود رد فعل أو القليل من اختبار وخز الجلد ؛ الحالات السلبية). وبالتالي ، يمكن اكتشاف الحالات الإيجابية بدقة معينة - ولكن ليس بشكل مثالي ، لأن بعض القياسات معيب إلى حد ما وتعطي قيمًا منخفضة عن طريق الخطأ للحالات الإيجابية أيضًا. إذا اقترح شخص ما تحسنًا في الإجراء لتحقيق قيم أعلى في المقياس X ، فسيكون من الممكن مقارنة الطريقتين في الحالات الإيجابية فقط: نظرًا لأن المقياس سيكون دائمًا ثابتًا (منخفضًا) في الحالات السلبية (الأشخاص الأصحاء) ، فإن القيم الأعلى للحالات الإيجابية تعني أن الإجراء سيكون له أيضًا كفاءة تشخيصية أفضل.
المشكلة هنا هي أن حجم التأثير لحساب الطاقة المحتمل هو بين شرطين إيجابيين ، والتي ليس لها تأثير مباشر على العواقب العملية في التشخيص. يساعد البرنامج الحالي من خلال توفير تقديرات لقيم الكفاءة التشخيصية (معدلات الكشف الصحيحة والمناطق تحت المنحنيات) لأحجام التأثير المعطاة بين الظروف الإيجابية وحدها.
استلهم هذا البرنامج فعليًا من دراسات اختبار المعلومات المخفية (CIT): يمكن أن تكشف CIT أن الشخص يعترف ببند التحقيق ذي الصلة (على سبيل المثال سلاح قتل محدد يستخدم في جريمة حديثة) من بين عناصر أخرى غير ذات صلة (على سبيل المثال الأسلحة الأخرى المعقولة) ، بناءً على مختلف الأسلحة ، على سبيل المثال ، الاستجابة للمسبار مقارنة بالعناصر غير المخصصة. نظرًا لأن الأشخاص الأبرياء لا يتعرفون على المسبار على أنه ذا صلة ، فإن استجاباتهم ستختلف في المتوسط بين المجس والعناصر غير ذات الصلة. وبالتالي ، استنادًا إلى اختلافات التحقيق الكبرى-الإشعال ( PI ) ، يمكن تمييز الأشخاص المذنبين عن تلك الأبرياء. من الأهمية بمكان ، نظرًا لأن PI دائمًا ما يكون حول الصفر بالنسبة للبطائمين ، فإن العديد من الدراسات تقارن الإصدارات المختلفة من CIT باستخدام مجموعات مذنبة فقط ، مع فهم أن مجموعة PI الكبيرة تعني لإصدار معين يعني أن الكفاءة التشخيصية ستكون أيضًا أفضل استخدام هذا الإصدار (أي أن الأشخاص الأكثر مذنبًا يمكن تمييزه بشكل صحيح عن تلك البريئة). ومع ذلك ، فإن الفرق في الوسط الحسابي بين مجموعتين مذنبين (أو SMD ذات الصلة) ليس له أي آثار عملية معقولة ، وبالتالي لا يمكن استخدامه لقرار متعلم بشأن حجم العينة. في الواقع ، استخدم 13 من أصل 24 دراسة تم جمعها في التحليل التلوي الأخير (Lukács & Specker ، 2020) مقارنة شرط أحادي ، ولم يتم الإبلاغ عن حساب السلطة المسبق لأحجام العينات ، وحتى تفسير أحجام التأثيرات الشهيرة في Cohen ، ولكن في نهاية المعايير التعرية النهائية ، مع عدم وجود معنى عملي مباشر (Cohen ، 1988 ؛ Lakens et al ، 2018).
الآن ، أبلغ هذا التحليل التلوي أيضًا عن متوسط SDS (استنادًا إلى 12 تجربة) للحالات (مجموعات مذنب) وضوابط (مجموعات بريئة) ، 33.6 و 23.5 ، على التوالي-لذلك يمكن استخدامها في تطبيق ESDI كقيم إدخال للحالة SD والتحكم في SD . ومع ذلك ، فإن استخدام القيمة الافتراضية لـ 1 لكلا SDS يعطي بالفعل نتائج متشابهة للغاية: بشكل عام ، فإن معرفة وتقديرات SD الدقيقة ليست حيوية (ما لم تكن نسبة SD / Control SD كبيرة جدًا أو صغيرة جدًا).
إعطاء 33.6 و 23.5 للحالة SD والتحكم في SD ، 4000 لحجم العينة ، وترك جميع الإعدادات الأخرى دون تغيير ، ستبدو المؤامرة المشتركة الرئيسية مثل:
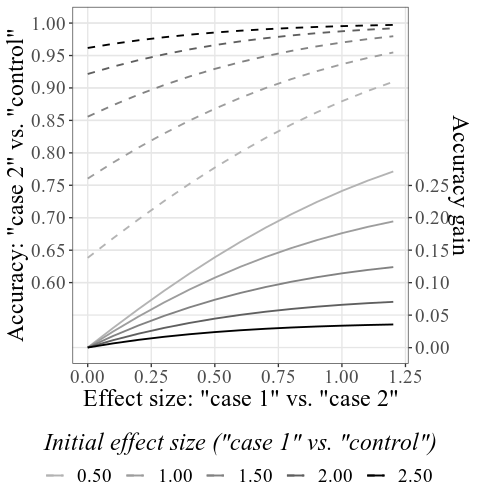
لاحظ أنه - كما هو موضح بالتفصيل بموجب القسم كيفية الاستخدام أعلاه - يتم حساب الدقة الأولية استنادًا إلى SMDs الأولية المحددة (انظر التسمية السفلية ؛ تحت إعدادات المؤامرة يمكن تغيير هذه التسمية لعرض الدقة بدلاً من SMDs). قد تختلف SMDs الناتجة قليلاً عن SMDs الواردة في الإعدادات ، نظرًا لعملية المحاكاة (مرة أخرى ، راجع كيفية الاستخدام للحصول على التفاصيل الفنية).
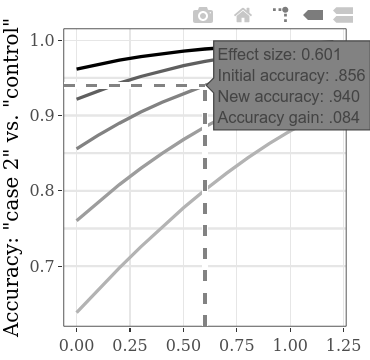
يمكن استكشاف زيادة الدقة الكلية أو الدقة المماثلة ، في وظيفة الزيادة بين الشرط (مذنب 1 مقابل 2) SMD ، بشكل منفصل على المخططات الفرعية التفاعلية. على سبيل المثال ، تحوم فوق الخط كما هو موضح أدناه ، توضح الملصق الذي يظهر أنه إذا وجدنا حجم تأثير (SMD) 0.601 بين نتائج مجموعتين مذنبين ، بالنظر إلى دقة أولية قدرها. إذا افترضنا أن الدقة الأولية (أي ، الدقة باستخدام الطريقة مع الكفاءة التشخيصية السفلية) لهذا النوع من CIT هي في الواقع حول .856 ، يمكننا استخدام قيم SMD على هذا الخط لحساب الطاقة. على سبيل المثال ، مع SMD 0.6 ، لقوة 0.9 ، فإن حجم العينة المطلوب لكل مجموعة هو 60 (للاختبار t غير المقيد مع alpha = .05). وبالتالي ، لاكتشاف إحصائيا زيادة ما لا يقل عن 0.084 في دقة الكشف ، يجب جمع ما مجموعه 120 شخصًا في الشرطين المذنبين.
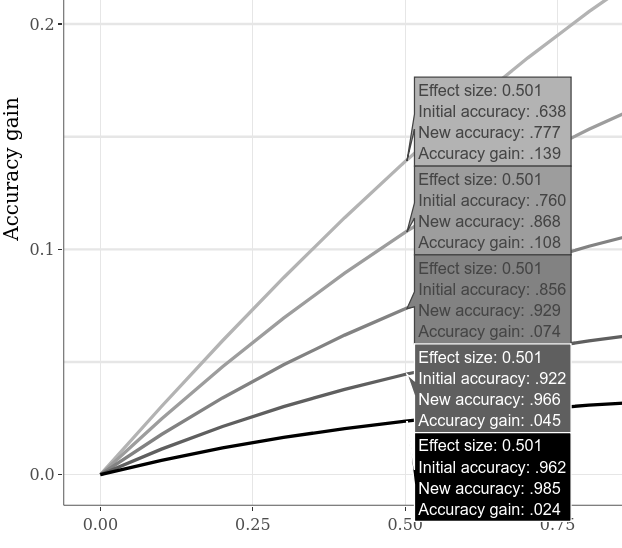
يمكن مقارنة الدقة الأولية البديلة ، على سبيل المثال ، بالتبديل إلى علامة التبويب المخططات الفرعية التفاعلية الكبيرة ، والنقر فوق خيار "مقارنة البيانات على Hover" في المؤامرة السفلية ، ونقل المؤشر أفقيًا على طول المؤامرة. يوضح المثال أدناه مكاسب دقة مختلفة عندما تكون "الحالة 1" "مقابل" الحالة 2 "SMD هي 0.5. نظرًا لأنه كان واضحًا بالفعل على مؤامرات المثال السابق ، فإن الدقة الأولية المنخفضة تتيح دائمًا زيادة دقة أكبر.
لاستكشاف المزيد من قيم البداية الأولية في نفس الوقت ، يمكن خفض إعداد الخطوة لـ "CASE 1" مقابل "التحكم" SMD ، مما يؤدي إلى المزيد من الخطوط على المؤامرة (وإلى زيادة وقت الحساب إلى حد ما). (ستؤدي الخطوة الخاصة بـ "الحالة 1" "مقابل" الحالة 2 "SMD إلى المزيد من نقاط البيانات الأفقية.)
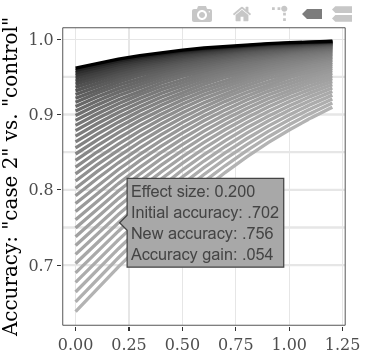
افتراضيًا ، يتم عرض معدلات بسيطة للكشف الصحيح (عدد جميع الموضوعات المصنفة بشكل صحيح مقسومًا على عدد جميع الموضوعات) لقياس "الدقة" ، لأن هذا ربما يكون المؤشر الأكثر وضوحًا لكفاءة التشخيص. يمكن تغييره إلى المنطقة أسفل المنحنى تحت علامة التبويب "قطعة الأرض" في اللوحة اليسرى. تحت نفس علامة التبويب ، يمكن أيضًا تخصيص ملصقات المؤامرة.
يمكن التحقق من الوظيفة الأساسية للبرنامج باستخدام حزمة shinytest لتشغيل بدلة اختبار آلية (على سبيل المثال بعد تقديم المساهمات). فقط قم بتشغيل shinytest::recordTest("/path/to/directory/") - حيث "/path/to/directory/" يجب استبداله بالمسار إلى دليل التطبيقات ، على سبيل المثال "C:/apps/esdi/" .
إذا كان لديك أي أسئلة أو ابحث عن أي مشكلات (الأخطاء أو الميزات المطلوبة) ، فاكتب بريدًا إلكترونيًا أو افتح مشكلة جديدة.
كوهين ، ج. (1988). تحليل القوة الإحصائية للعلوم السلوكية (الطبعة الثانية). Hillsdale ، NJ: Erlbaum.
Lakens ، D. (2013). حساب أحجام التأثير والإبلاغ عن الإبلاغ لتسهيل العلوم التراكمية: التمهيدي العملي لاختبارات t و ANOVAs. الحدود في علم النفس ، 4. https://doi.org/10.3389/fpsyg.2013.00863
Lakens ، D. ، Scheel ، Am ، & Isager ، PM (2018). اختبار التكافؤ للبحث النفسي: برنامج تعليمي. التقدم في الأساليب والممارسات في العلوم النفسية ، 1 (2) ، 259-269. https://doi.org/10.1177/2515245918770963
Perugini ، M. ، Gallucci ، M. ، & Costantini ، G. (2018). تمهيدي عملي لتحليل الطاقة للتصميمات التجريبية البسيطة. المراجعة الدولية لعلم النفس الاجتماعي ، 31 (1) ، 20. https://doi.org/10.5334/irsp.181
استشهد بهذا البرنامج على النحو التالي:
Lukács ، G. ، & Specker ، E. (2020). مسائل التشتت: التشخيص والتحكم في محاكاة الكمبيوتر في دراسات اختبار المعلومات المخفية. PLOS ONE ، 15 (10) ، E0240259. https://doi.org/10.1371/journal.pone.0240259