En utilisant des simulations pour les valeurs d'entrée données, cette application R Shiny R montre comment l'efficacité diagnostique (telle que mesurée par les taux de détection correcte ou les zones dans les courbes) change par rapport à la différence moyenne standardisée ( SMD ) Différences de taille d'effet entre les cas à condition unique (lorsque ceux-ci sont directement comparés par manque de contrôles).
La demande est disponible en ligne (pour être simplement ouvert dans n'importe quel navigateur Web): https://gasparl.shinyapps.io/esdi/
Cependant, il est également facile de l'exécuter à partir de votre PC. Il vous suffit d'exécuter la commande suivante dans R :
shiny :: runGitHub( " esdi " , " gasparl " )` Pour cette dernière alternative, si vous ne les avez pas déjà, vous devez installer R , puis installer le package shiny dans R EG en entrant install.packages("shiny") dans la console. Copiez ensuite la ligne shiny::runGitHub("esdi", "gasparl") par exemple dans la console et appuyez sur Entrée. Les composants nécessaires seront téléchargés automatiquement et l'application s'ouvrira dans une nouvelle fenêtre.
Enfin, pour utiliser l'application à tout moment sans accès Internet, vous pouvez télécharger l'intégralité du référentiel (ou simplement app.r ) et exécuter le code dans le fichier app.r. Pour cela, vous devrez installer tous les packages R utilisés dans le code (répertorié dans les premières lignes).
Pour saisir rapidement l'essence de l'application, consultez l' exemple de la section ci-dessous ou consultez les antécédents pour la motivation générale. Ce qui suit ici est une explication technique détaillée.
Les seuls paramètres qui influencent la relation clé SMD-Diagnostics sont le (rapport des émires-types (SDS) (rapport) des valeurs prédictives pour les cas et pour les contrôles , qui représentent le SD généralement assumé pour les données des cas positifs et pour les données des contrôles, respectivement (encore une fois, pour plus d'explication, voir les antécédents et les exemples ci-dessous). Le SDS doit être estimé sur la base des SD typiques pour les cas et les contrôles dans la zone de recherche donnée. Cependant, les différences en SD ont relativement peu d'impact sur les résultats, et pour la plupart des cas (lorsque le SD n'est pas connu ou ne peut pas être facilement estimé), il peut être supposé que laisser les paramètres par défaut ( 1 pour les deux SD) donnera toujours des résultats approximativement corrects (sauf si le cas SD / Control SD peut être très grand ou très petit). En d'autres termes, les paramètres par défaut de ce logiciel sont probablement applicables pour la plupart des scénarios.
Sur la base des SDS donnés, les moyennes des échantillons sont automatiquement calculées pour chacun des SMD spécifiés dans les autres paramètres. Remarque: Pour être bref et pourtant éviter l'abréviation, SMD (différence moyenne standardisée) est indiqué comme «taille de l'effet» pour les étiquettes d'option et de tracé sur l'interface. Des ensembles de données sont générés pour toutes les différentes moyennes (en utilisant les deux SD constantes) avec une distribution normale presque parfaite. La spécification des SMD est assez simple: une valeur de départ, une valeur finale et une étape doivent être données. Par exemple, un début de 0.2 , une fin de 0.6 et un pas de 0.1 définiront les SMD suivants: 0.2 , 0.3 , 0.4 , 0.5 , 0.6 . Un pas plus petit (ou plus de démarrage et de fin éloigné) signifie plus de points de données à calculer, et donc ces paramètres peuvent augmenter considérablement le temps de calcul.
Il est important de garder à l'esprit la différence entre (a) SMD entre les conditions uniques ("Cas 1" contre "cas 2") et (b) le SMD entre le cas et le contrôle d'une condition unique ("cas" vs "contrôle"). Le premier (a) indique des différences d'efficacité diagnostique entre deux méthodes de diagnostic (par exemple une ancienne méthode et une nouvelle méthode améliorée), tandis que la seconde (b) n'est qu'une mesure alternative pour l'efficacité diagnostique dans une méthode donnée (par exemple, l'efficacité diagnostique de l'ancienne méthode), et ce dernier cas est toujours plus grande "Contrôle directement avec la corrélation toujours avec une plus grande signification des mesures d'efficacité diagnostique (donc le case" Contrôle "SDD avec une corrélation toujours plus grande avec les mesures d'efficacité diagnostique (donc la vitesse" Contrôle "SDD toujours avec la caractéristique de l'efficacité diagnostique (SO ARRIÈRE" CONTROSS "SEMPORT SIGNIFICATIVE LA CORRÉLÉATION POUR TOUJOURS ATTABLE de détection correcte et de surface plus grande sous la courbe).
Le SMD initial "Case 1" vs "Control" représente les efficacités de diagnostic supposées de la méthode à améliorer (méthode 1). (Remarque: il est possible, mais il n'a pas de sens dans la pratique d'inclure zéro pour la valeur de démarrage, sauf si à des fins de démonstration, car cela signifierait que la méthode 1 fonctionne au niveau du hasard, il est donc inutile en premier lieu.) Les graphiques décrivent la méthode améliorée (méthode 2) Efficacité de diagnostic ( précision 2 "Cas 2" Vs. " (Remarque: Pour plus de clarté, il est toujours bon de conserver la valeur de démarrage du SMD "Case 1" contre "Case 2" à zéro, qui illustre ensuite le point de départ où il n'y a pas encore de différence entre les deux méthodes.) Ensuite, il peut être vu comment les augmentations de la SMD entre l'initiation "Cas 1" et "Cas 2" ont conduit à certaines étendus de la précision.
Les valeurs sont représentées de deux manières différentes: en tant que précision totale et en tant que précision gagnée . La précision acquise est calculée simplement comme une précision totale moins la précision initiale (méthode 1). Le tracé combiné contient les deux types, tandis que les sous-intrigues représentent ces types séparément et peuvent être explorés de manière interactive en survolant les lignes avec le curseur pour lire les valeurs précises des SMD et des précisions aux points donnés sur le tracé (voir l' exemple de la section ci-dessous).
Étant donné que la taille de l'échantillon n'est pas infinie, la distribution normale ne peut jamais être vraiment parfaite, et donc il y aura de petits écarts dans les résultats SMD calculés par rapport aux paramètres SMD donnés: par exemple, un SMD initial peut être donné comme 0.5 dans les paramètres, mais les résultats réels peuvent être, par exemple, 0.51 . La taille de l'échantillon (nombre de points de données générés) peut être définie sous l'étiquette Sample size : un nombre plus grand conduit à un temps de calcul quelque peu accru, mais des résultats plus précis. Une taille d'échantillon d'environ 4000 donnera généralement de la précision jusqu'à deux chiffres fractionnaires, tandis que Ca. 15000 peuvent être précis jusqu'à trois chiffres fractionnaires. Surtout, quelle que soit la taille de l'échantillon (et la correspondance des paramètres et des résultats), la relation de SMD et de diagnostic pour les résultats donnés est toujours exacte et correcte.
Les paramètres de tracé sont liés à la représentation des données et devraient être explicites. Toutes les valeurs pour le calcul des tracés sont disponibles sous l'onglet Table dans une table de données interactive.
Une analyse de puissance prospective ( a priori ) pour déterminer la taille de l'échantillon requise est cruciale pour les expériences comportementales (par exemple, Perugini, 2018). Pour déterminer le plus petit effet d'intérêt requis pour l'analyse de puissance, le moyen idéal est de s'appuyer sur la justification objective (Lakens, 2013; Lakens et al, 2018). Par exemple, pour comparer deux méthodes de diagnostic différentes, on peut considérer les implications de la vie réelle d'une augmentation donnée du taux de détection correcte d'une maladie par rapport aux coûts de la taille de l'échantillon requis pour montrer des preuves statistiques de cette augmentation donnée. Un chercheur peut prendre la décision éclairée et minutieuse qu'il vaut la peine de collecter, disons, 120 participants pour détecter une augmentation d'au moins 8% de précision de détection: une augmentation de 2% ou même 0,1% pourrait également avoir un avantage réel important, mais en raison de ressources limitées, elle ne vaut pas la peine de collecter les tailles d'échantillon beaucoup plus importantes nécessaires pour détecter de tels changements plus petits.
Cependant, l'implication pratique n'est pas toujours aussi simple à évaluer. Dans un scénario spécifique dans la conception expérimentale, deux méthodes de diagnostic peuvent être valablement comparées à l'aide de cas à condition unique, en omettant des contrôles (aka "de base" ou "condition négative") pour épargner les ressources. Ce scénario peut se produire dans l'un des nombreux domaines appliquant une classification binaire, peut-être le plus caractéristique en médecine. Une maladie hypothétique peut être diagnostiquée avec une mesure continue X , qui est généralement plus élevée pour les personnes atteintes d'une maladie donnée (comme une petite bosse ou une rougeur en réaction à un test de piqûre cutanée; cas positifs), alors qu'il est généralement le même pour les personnes en bonne santé (telles que non ou peu de réaction à un test de piqûre cutanée; cas négatifs). Ainsi, des cas positifs peuvent être détectés avec une certaine précision - mais pas parfaitement, car certaines des mesures sont dans une certaine mesure défectueuses et donnent également des valeurs à tort dans des cas positifs. Si quelqu'un proposait une amélioration de la procédure pour obtenir des valeurs plus élevées dans la mesure X , il serait possible de comparer directement les deux méthodes sur des cas positifs uniquement: car la mesure sera toujours constante (faible) dans les cas négatifs (personnes en bonne santé), des valeurs plus élevées pour les cas positifs signifie que la procédure aura également une meilleure efficacité diagnostique.
Le problème ici est que la taille de l'effet pour le calcul potentiel de puissance se situe entre deux conditions positives, qui n'ont aucune implication directe pour les conséquences pratiques dans les diagnostics. Le logiciel actuel aide en fournissant des estimations pour les valeurs d'efficacité diagnostique (taux de détection corrects et zones dans les courbes) pour les tailles d'effet données entre les conditions positives.
Ce logiciel a en fait été inspiré par des études de test d'information dissimulées (CIT): le CIT peut révéler qu'une personne reconnaît un élément de sonde pertinent (par exemple, une arme de meurtre spécifique utilisée dans un crime récent), entre autres, des objets non pertinents (par exemple d'autres armes plausibles), basées sur différentes, par exemple plus lentement à la sonde par rapport aux éléments imprudents. Étant donné que les innocents ne reconnaissent pas la sonde comme pertinente, leurs réponses ne seront en moyenne pas en moyenne entre la sonde et les éléments non pertinents. Par conséquent, sur la base des différences plus importantes de sonde-minus-irrelinant ( PI ), les coupables peuvent être distingués des innocents. Surtout, puisque le PI est toujours autour de zéro pour les innocents, de nombreuses études comparent différentes versions du CIT en utilisant uniquement des groupes de culpabilité, avec la compréhension que le plus grand groupe PI signifie pour une version donnée signifie que l'efficacité diagnostique sera également mieux en utilisant cette version (c'est-à-dire des personnes plus coupables, peut être correctement distinguée des innocents). Cependant, la différence dans la moyenne arithmétique entre deux groupes coupables (ou le SMD apparenté) n'a pas vraiment d'implication pratique judicieuse, et donc elle ne peut pas être utilisée pour une décision instruite sur la taille de l'échantillon. En effet, 13 études sur 24 collectées dans une méta-analyse récente (Lukács & Specker, 2020) ont utilisé une comparaison unique, aucune n'a signalé de calcul de puissance antérieure pour les tailles d'échantillon, et même l'interprétation des tailles d'effet n'étaient basées sur le célèbre de Cohen mais dans la fin des commandes arbitraires, sans signification réalisée (Cohen, 1988; Lakens et al, 2018).
Désormais, cette méta-analyse a également signalé une SDS moyenne (sur la base de 12 expériences) pour les cas (groupes coupables) et des témoins (groupes innocents), 33.6 et 23.5 , respectivement - ils peuvent donc être utilisés dans l'application ESDI comme valeurs d'entrée pour les cas SD et les témoins SD . Cependant, l'utilisation de la valeur par défaut de 1 pour les deux SDS donne en fait des résultats très similaires: en général, connaître et donner des estimations SD précises n'est pas vitale (sauf si le rapport SD / Control SD peut être très grand ou très petit).
Donnant les 33.6 et 23.5 pour Case SD et Control SD , 4000 pour la taille de l'échantillon , et laissant tous les autres paramètres inchangés, le tracé combiné principal ressemblera à ceci:
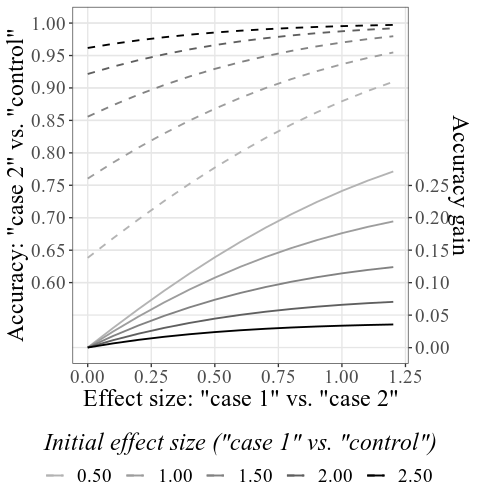
Notez que - comme expliqué en détail dans la section comment utiliser comment ci-dessus - les précisions initiales sont calculées en fonction des SMD initiaux donnés (voir l'étiquette inférieure; sous les paramètres de tracé, cette étiquette peut être modifiée pour afficher des précisions au lieu de SMD). Les SMD résultant peuvent être légèrement différés des SMD donnés dans les paramètres, en raison du processus de simulation (encore une fois, voir comment utiliser pour les détails techniques).
L'augmentation de la précision totale ou de la précision analogue a acquis une précision , en fonction de l'augmentation entre les conditions (coupable 1 contre coupable 2) SMD, peut être explorée séparément sur les sous-intrigues interactives. Par exemple, planant sur la ligne comme indiqué ci-dessous, l'étiquette qui apparaît montre que si nous trouvons une taille d'effet (SMD) de 0,601 entre les résultats de deux groupes coupables, étant donné une précision initiale de 0,856 (le taux de personnes correctement détectées, à la fois coupable et innocent), la précision augmente de 0,084 (ce qui donne une nouvelle précision de 0,940). Si nous supposons que la précision initiale (c'est-à-dire, la précision utilisant la méthode avec l'efficacité diagnostique inférieure) de ce type de CIT est en effet généralement autour de .856, nous pouvons utiliser les valeurs SMD sur cette ligne pour le calcul de la puissance. Par exemple, avec le SMD 0,6, pour une puissance de 0,9, la taille de l'échantillon requise par groupe est de 60 (pour un test t non apparié avec alpha = 0,05). Par conséquent, pour détecter statistiquement une augmentation d'au moins 0,084 dans la précision de la détection, un total de 120 personnes doivent être collectés pour les deux conditions coupables.
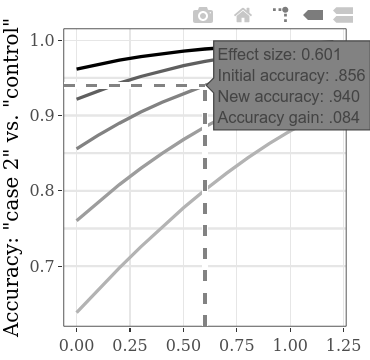
Des précisions initiales alternatives peuvent être comparées par, par exemple, en passant à l'onglet de sous-intrigues interactifs , en cliquant sur l'option "Comparer les données sur le survol" sur le tracé inférieur et en déplaçant le curseur horizontalement le long du tracé. L'exemple ci-dessous montre divers gains de précision lorsque le SMD "Case 1" contre "Cas 2" est de 0,5. Comme il était déjà apparent sur les complots d'exemples précédents, une précision initiale plus faible permet toujours un gain de précision plus important.
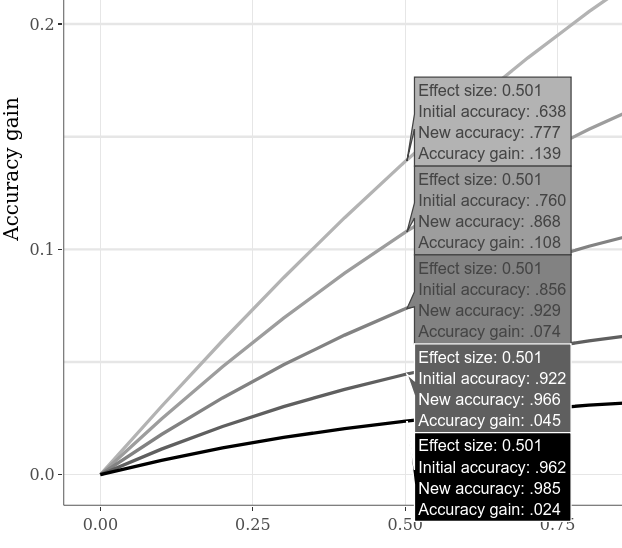
Pour explorer plus de valeurs de départ initiales en même temps, le paramètre de pas pour le SMD "Cas 1" contre "Control" peut être abaissé, conduisant à plus de lignes sur le tracé (et à un temps de calcul quelque peu accru). (L'étape du SMD "Case 1" vs "Cas 2" entraînera de manière analogue des points de données plus horizontaux.)
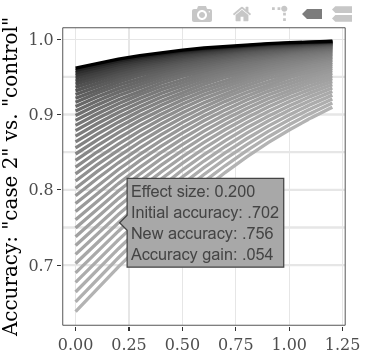
Par défaut, des taux simples de détection correcte (nombre de tous les sujets correctement classés divisés par le nombre de tous les sujets) sont affichés pour la mesure de "précision", car il s'agit probablement de l'indicateur le plus simple de l'efficacité diagnostique. Il peut être changé en zone sous la courbe sous l'onglet "Plot" dans le panneau de gauche. Dans le même onglet, les étiquettes de tracé peuvent également être personnalisées.
La fonctionnalité de base du logiciel peut être vérifiée à l'aide du package shinytest pour exécuter une combinaison de test automatisée (par exemple après avoir apporté des contributions). Il suffit d'exécuter shinytest::recordTest("/path/to/directory/") - où "/path/to/directory/" doit être remplacé par le chemin d'accès au répertoire des applications, par exemple "C:/apps/esdi/" .
Si vous avez des questions ou trouvez des problèmes (bogues, fonctionnalités souhaitées), écrivez un e-mail ou ouvrez un nouveau problème.
Cohen, J. (1988). Analyse statistique de la puissance pour les sciences du comportement (2e éd.). Hillsdale, NJ: Erlbaum.
Lakens, D. (2013). Calcul et indication de tailles d'effet pour faciliter la science cumulative: une amorce pratique pour les tests t et les ANOVA. Frontiers in Psychology, 4. https://doi.org/10.3389/fpsyg.2013.00863
Lakens, D., Scheel, AM et Isager, PM (2018). Test d'équivalence pour la recherche psychologique: un tutoriel. Advances in Methods and Practices in Psychological Science, 1 (2), 259-269. https://doi.org/10.1177/251524591870963
Perugini, M., Gallucci, M. et Costantini, G. (2018). Une introduction pratique à l'analyse de puissance pour des conceptions expérimentales simples. Revue internationale de la psychologie sociale, 31 (1), 20. https://doi.org/10.5334/IRSP.181
Citez ce logiciel comme:
Lukács, G. et Specker, E. (2020). Dispersion Matters: Diagnostics and Control Data Simulation informatique dans les études de test d'informations dissimulées. PLOS ONE, 15 (10), E0240259. https://doi.org/10.1371/journal.pone.0240259