space as scale

пространство как масштаб

хранилище для развития концепции пространства как масштаба, а не как расстояние

Пространство как расстояние - неправильная абстракция

Концепция пространства развивалась в течение тысячелетий construction и movement .

Чтобы выполнять строительные работы, мы измеряем:

• distance между объектами или точками
• area поверхности
• size или volume объекта
• height объекта, точки или поверхности
• длина и высота, связанные с штриховыми устройствами
• сила веревки на основе площади поперечного сечения
• и т. д.

Необходимость понимания физических тел в motion , как небесных, так и земных, привела к таким понятиям:

• скорость
• ускорение
• сила
• давление
• кинетическая и потенциальная энергия
• власть

Все требуют измерения расстояния в различном количестве размеров в пространстве.

Ньютон начал с этого пространства как данное, как абсолютная среда, через которую все существует и происходит: an arena we measure as distance .

Следовательно, классическая физика построила свою структуру законов и правил вокруг пространства, которое состоит из измеренных или измеримых расстояний, с помощью которых действий сил и энергии обмениваются.

Однако это пространство nothing делает. Это просто что -то, что we измеряем. Это inert . Это ничего не do . Это объясняет, почему силы были введены в act в этом пространстве, придавая энергию и способствуя изменения, т.е. causation .

Но ...

Существует причинно -следственный обмен между big и small , который не фиксируется путем измерения нормального линейного расстояния, а путем измерения scale расстояния между ними, то есть их relative размер. В широком диапазоне явлений, от супер -галактик кластеров и планетарных туманных, до форм растений и органов животных и паттернов роста, до молекул ДНК и атомных орбиталей: между окружающей средой и составляющей частью. Большое поглощение и охватывание меньшего. Каждый формирует другого внизу и выше в иерархии.

Вопросы, о которых у меня есть:

• Как маленькая и большая взаимодействие и обменубуация?
• Как выглядит такое взаимодействие?
• Какие характеристики у него есть?
• Как это можно описать?
• Как мы изучаем этот вид взаимодействия?
• Как мы изучаем иерархию в физике?

Если наши вопросы связаны не с конструкцией и движением, а о growth и contraction , мы не должны бороться с той же концепцией пространства - то есть то, что измеряется на линейном расстоянии: it would be the wrong abstraction .

Если мы строим физику из пространства, которое опосредует причинно -следственную связь между большим и маленьким - т.е. описывает, как вещи в разных масштабах растут, связываются и меняются вместе:

• В какую динамику мы прибываем?
• Что бы эта динамика была способна описать?
• Какие концепции мы найдем, параллельно скорости, ускорению, силе, давлению, энергии и мощности?
• Что они значат?
• Какие еще неизвестные, в дополнение к вышеуказанным, мы найдем?

Мы можем начать с рисования этого пространства и аннотировать его с тем, что мы знаем:

Рис (1) - масштаб и относительное расстояние

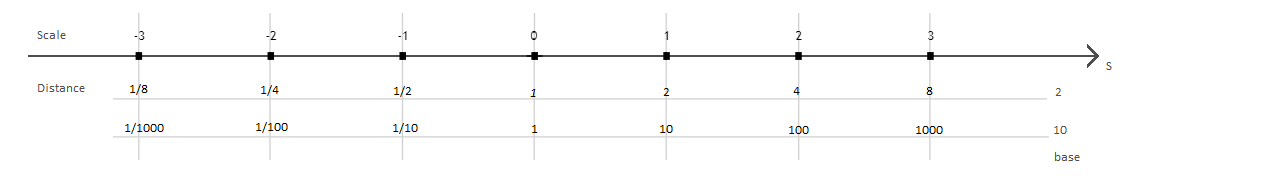
Если единица шага в масштабе в положительном направлении соответствует умножению связанного измерения (здесь расстояние) с базовым значением (то есть становится экспоненциально больше). Шаг единицы в отрицательном направлении соответствует делению значения на основание (то есть становится экспоненциально меньше).

Рис (1) показывает:

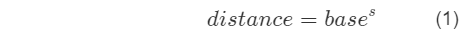
где s - значение масштаба.

Если я хочу описать объект в этом пространстве, я описываю его иерархическую структуру. Сам объект всегда сидит в точке 0, окруженный его непосредственным соседством: более крупная среда, непосредственно окружающая его, и его меньшие компоненты.

Идея состоит в том, что в любое время, когда наблюдатель хочет что -то описать, они корректируют масштаб, так что они описывают, находится в точке 0 (размер 1, независимо от того, какая база используется).

Другими словами: наше описание сосредотачивает масштаб вокруг его дескриптора. Например, описывает дом, где находится дом, где находится дом (его большая среда, улица, район и т. Д.), Его комнаты и их содержимое (его меньшие и меньшие размеры).

В этот момент мы можем найти таблетки Алисы довольно удобными:

one pill makes you larger, and one pill makes you small

.. и вот кикер:

and the ones that mother gives you, don't do anything at all

На самом деле, эти таблетки могут восстановить вас до вашего normal размера, поскольку ваша мать похожа на точку отсчета на масштабной земле.

Итак, давайте повторим, что это значит:

Чтобы описать объект, возьмите таблетку, которая делает вас своим размером, и вы становитесь вместе с тем, что описывается, в точке 0 в масштабе. Сделайте шаг вправо, и это умножает ваш размер на основание, которое вы выбрали для описания, которое вы описываете. Шаг слева - наоборот, и вы становитесь меньше по базовым значениям.

Это настаивает на том, что наблюдатель описывает объект с точки зрения своей собственной шкалы, воспроизводит субъективную природу наблюдения и описания. Описание всегда с точки зрения определенной шкалы.

Теперь мы можем получить показатели изменений и посмотреть, что мы получаем.