space as scale

Espaço em escala

repositório para evoluir o conceito de espaço como escala, em vez de distância

Espaço como distância é a abstração errada

O conceito de espaço evoluiu através de milênios de construction e movement .

Para fazer o trabalho de construção, medimos:

• A distance entre objetos ou pontos
• a area de uma superfície
• o size , ou volume , de um objeto
• a height de um objeto, ponto ou superfície
• comprimentos e alturas envolvidas em dispositivos pivô
• força de corda com base na área da seção transversal
• etc.

A necessidade de entender os corpos físicos em motion , celestial e terrestre, levou a conceitos como:

• velocidade
• aceleração
• vigor
• pressão
• energia cinética e potencial
• poder

Todos requerem a distância de medição em um número variável de dimensões no espaço.

Newton começou com esse espaço como um dado, como o meio absoluto pelo qual tudo existe e acontece: an arena we measure as distance .

Portanto, a física clássica construiu sua estrutura de leis e regras em torno de um espaço que consiste em distâncias medidas ou mensuráveis, através das quais as forças agem, e as energias são trocadas.

No entanto, esse espaço não faz nothing . Está lá como algo we . É inert . Não do nada. Isso explica por que as forças foram introduzidas para act nesse espaço, transmitindo energia e efetivando mudanças - ou seja, causation .

Mas ...

Há uma troca causal entre big e small que não é capturada pela medição da distância linear normal, mas medindo a distância scale entre eles, ou seja, seu tamanho relative . Em uma ampla gama de fenômenos, de grupos de super galáxias e nebulosas planetárias, a formas de órgãos e padrões de crescimento de plantas e animais, a moléculas de DNA e orbitais atômicos: parece haver um fio bastante entre o ambiente e a parte constituinte. O maior envolvimento e envolvendo o menor. Cada um moldando o outro abaixo e acima na hierarquia.

As perguntas que tenho são sobre:

• Como a causalidade pequena e a grande interage e troca?
• Como é essa interação?
• Que características ele tem?
• Como isso pode ser descrito?
• Como estudamos esse tipo de interação?
• Como estudamos uma hierarquia em física?

Se nossas perguntas não são sobre construção e movimento, mas sobre growth e contraction , não devemos ter que lidar com o mesmo conceito de espaço - ou seja, o que é medido a uma distância linear: it would be the wrong abstraction .

Se construirmos uma física a partir de um espaço que medeia a causa entre grande e pequena - ou seja, descreve como as coisas em diferentes escalas crescem, se relacionam e mudam juntas:

• Em que dinâmica chegamos?
• O que essa dinâmica seria capaz de descrever?
• Que conceitos encontraríamos, paralelos à velocidade, aceleração, força, pressão, energia e poder?
• O que eles significariam?
• Que outras incógnitas, além das acima, encontraríamos?

Podemos começar ganhando esse espaço e anotando -o com o que sabemos:

Fig (1) - Escala e distância relativa

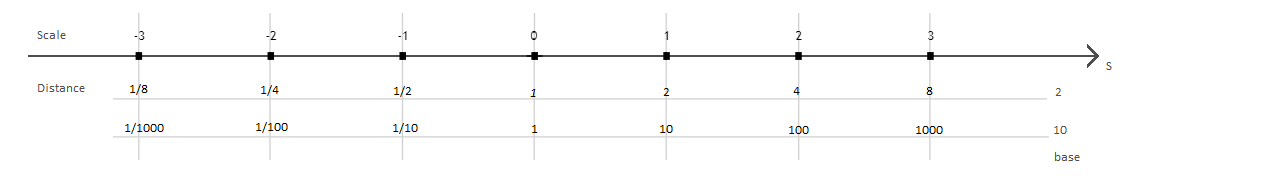
onde uma etapa de unidade em escala na direção positiva corresponde à multiplicação da dimensão associada (aqui distância) com o valor base (ou seja, se tornando exponencialmente maior). Uma etapa da unidade na direção negativa corresponde à divisão do valor pela base (ou seja, tornando -se exponencialmente menor).

Fig (1) mostra:

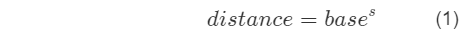
onde s é o valor da escala.

Se eu quiser descrever um objeto neste espaço, descrevo sua estrutura hierárquica. O objeto em si está sempre sentado no ponto 0, cercado por seu bairro de escala imediata: o ambiente maior imediatamente ao redor e seus componentes menores.

A idéia aqui é que, sempre que um observador deseja descrever algo, eles ajustam a escala, então o que está descrevendo é no ponto 0 (tamanho 1, independentemente da base usada).

Em outras palavras: nossa descrição centra a escala em torno de seu descritor. Por exemplo, descrever uma casa começa onde a casa está (seu ambiente maior, a rua, o bairro etc.), seus quartos e seu conteúdo (suas dimensões cada vez menores).

Neste ponto, podemos achar que as pílulas de Alice são bastante úteis:

one pill makes you larger, and one pill makes you small

.. e aqui está o kicker:

and the ones that mother gives you, don't do anything at all

Na verdade, esses comprimidos podem restaurá -lo ao seu tamanho normal , pois sua mãe é como um ponto de referência na terra da escala.

Então, vamos recapitular o que isso significa:

Para descrever um objeto, tome uma pílula que faz de você o seu tamanho e você se torna, juntamente com o que está sendo descrito, no ponto 0 na escala. Dê um passo para a direita, e isso multiplica seu tamanho pela base que você escolheu para a dimensão que está descrevendo. Um passo à esquerda é o inverso e você fica menor pelo valor base.

Essa insistência, que o observador descreve um objeto do ponto de vista de sua própria escala, reproduz a natureza subjetiva da observação e da descrição. Uma descrição é sempre do ponto de vista de uma escala específica.

Agora podemos derivar taxas de mudança e ver o que recebemos.