A simple e-book recommendation system based on the SSM framework and item collaborative filtering algorithm (ItemCF)
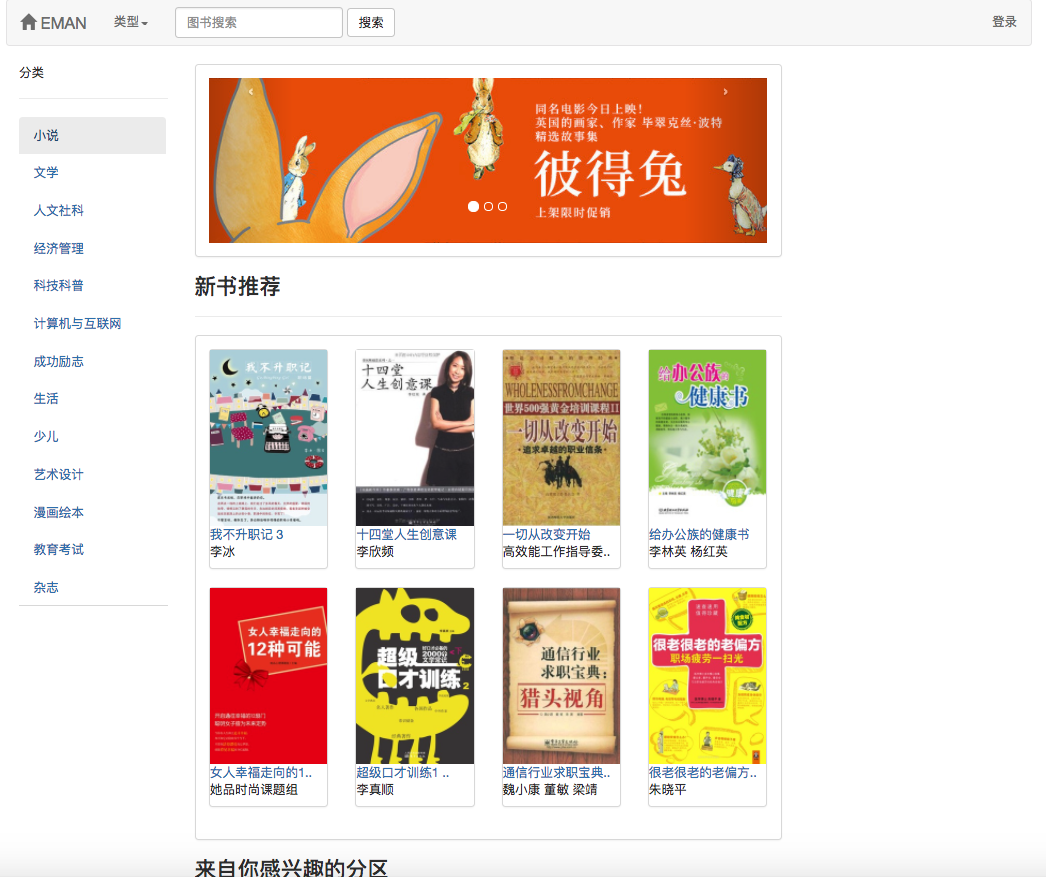
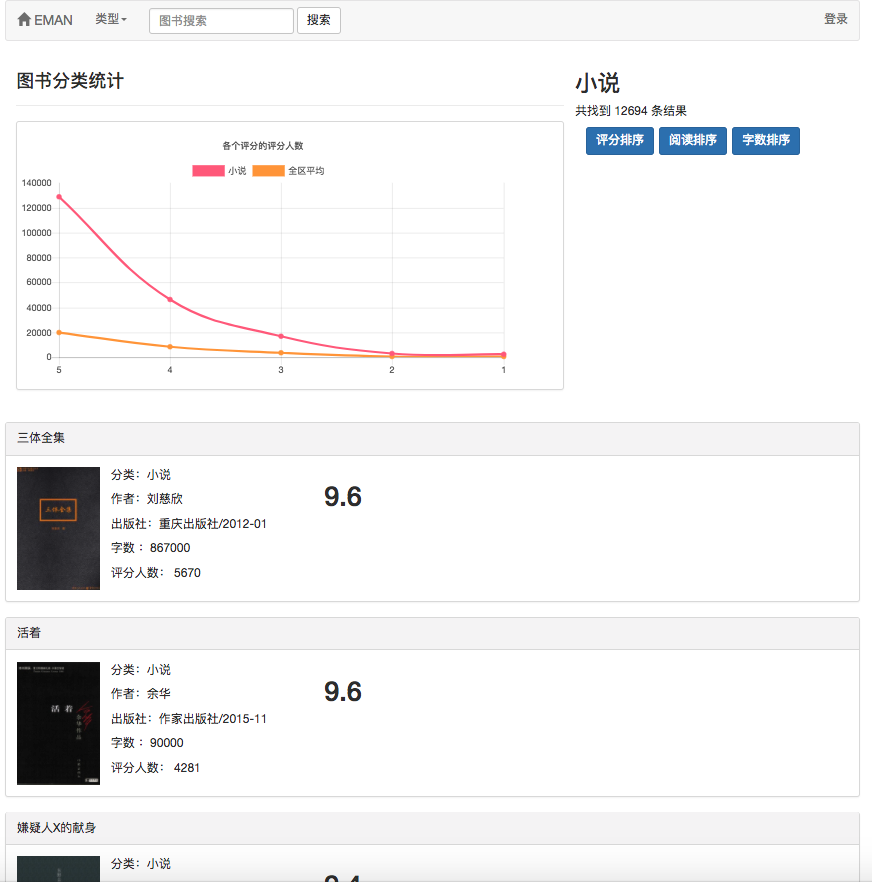
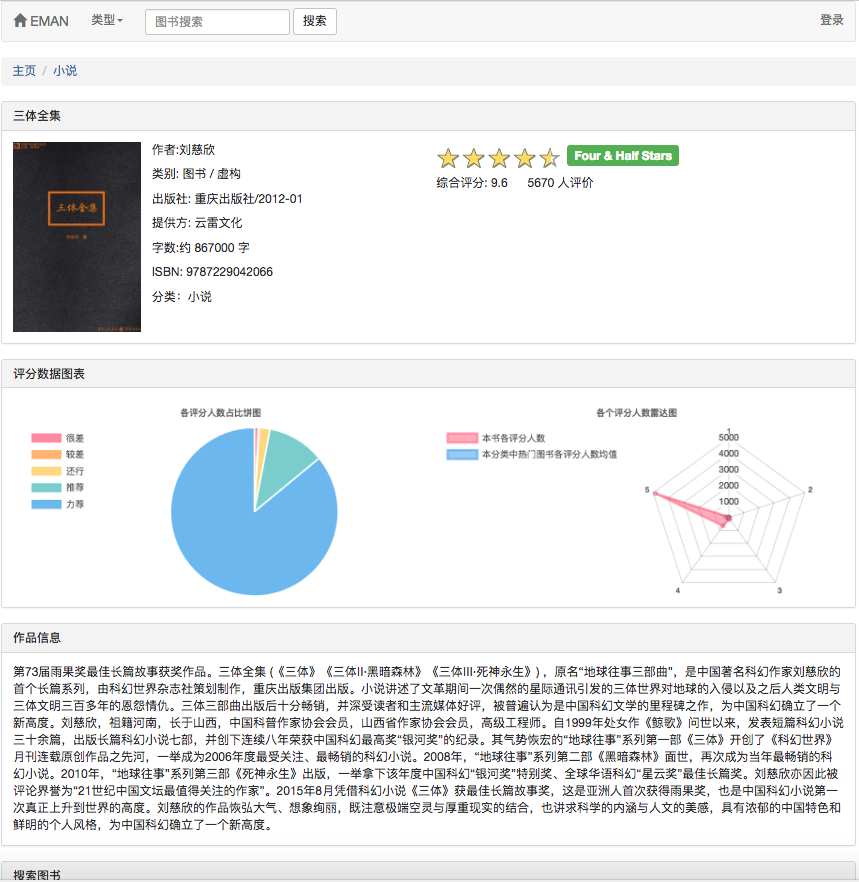
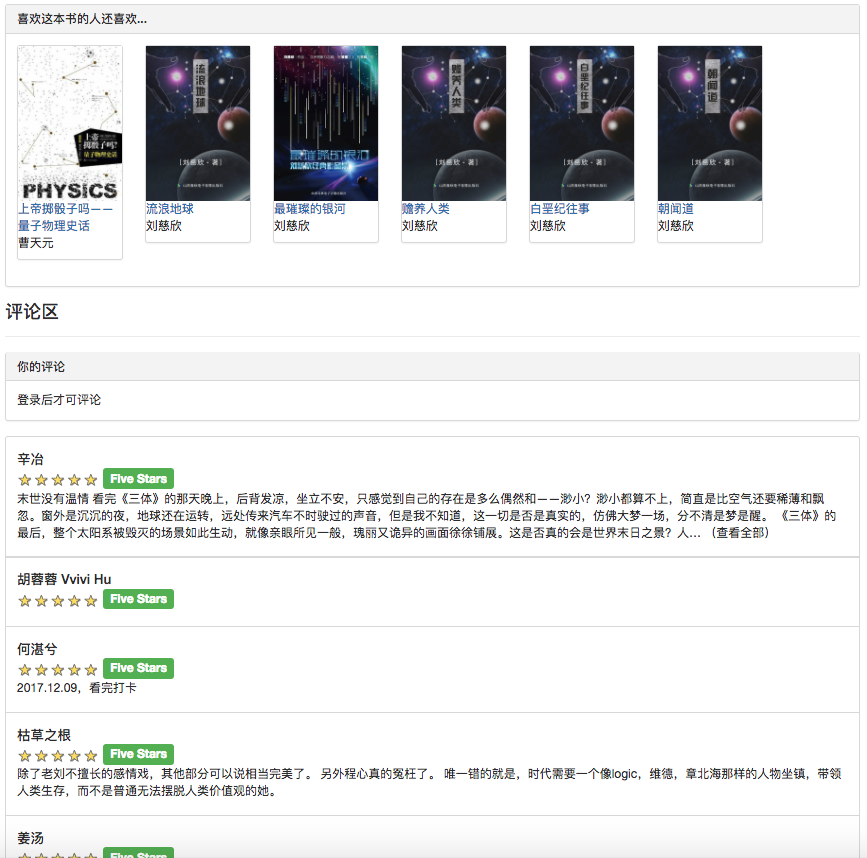

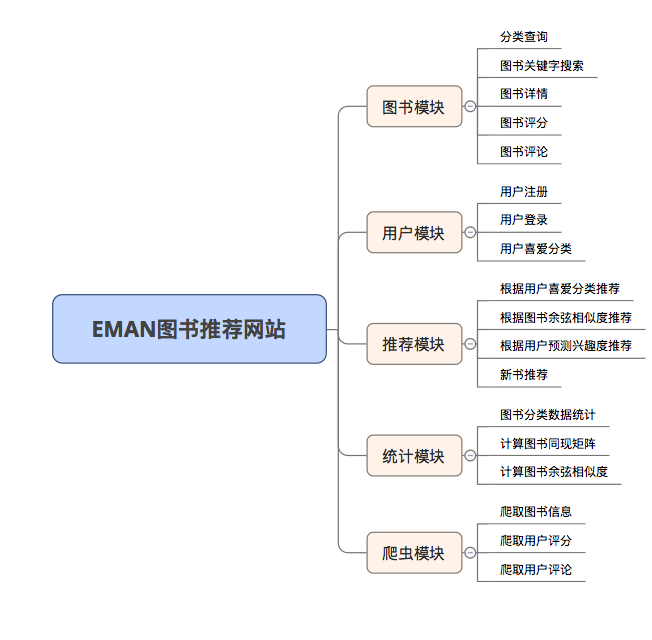
Because some recommendation algorithms need to use the user's favorite data as parameters. If the user is not logged in, the recommendation strategy for tourists will be adopted. If the user is logged in, the recommendation policy for the logged-in user is adopted. If the logged-in user has a partition record of interest in the database, a recommendation from the partition you are interested in will be added. Therefore, the recommendation strategy is divided into two situations: whether to log in or not.
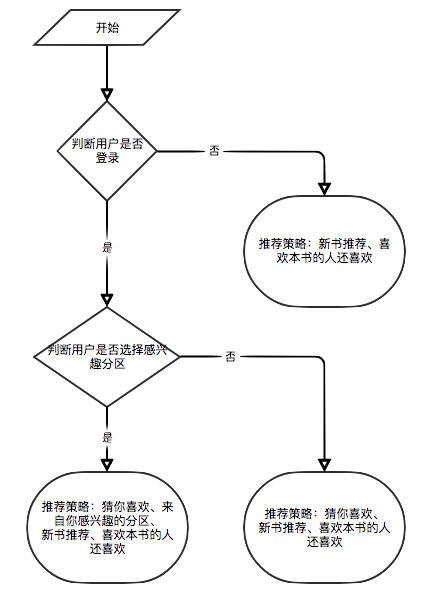
If the user is not logged in, the user rating display strategy for tourists will be adopted. If the user is logged in, the user rating display policy for the logged in user is adopted. If the logged-in user has already scored the e-book on the current details page, its rating record will be displayed.
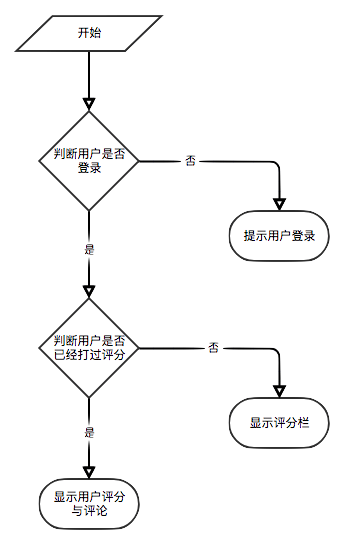
As shown in the use case diagram, there are three basic users in this system. These are tourists, registered users, and administrators. Visitors can visit the homepage of the e-book recommendation platform, user registration page, and view the e-book page. The function of registering users is that they can rate and comment on e-books and recommend e-books determined by the user's predicted interest. Administrators can regularly use the crawler module to update e-book information and use the statistics module to update classified statistics, e-book co-occurrence matrix and e-book cosine similarity matrix.

Considering that there is a cold start problem with this algorithm. That is, for new users, they often lack rating data, which leads to the recommendation based on the user's predicted interest level and cannot be smoothly carried out. To solve this problem, I added a module to directly use the cosine similarity matrix w to directly perform similar e-book recommendations, so that unregistered users and new users can better obtain recommendations. As for the sparse data matrix problems in collaborative filtering algorithms, some unpopular e-books may have no user ratings, low e-book correlation, and some users have few e-book ratings. To solve this problem, add a new book recommendation module to the homepage to better recommend e-books that have no rated; add a partition recommendation module to recommend e-books based on the user's interest in order to increase the interest of specific users to recommend e-books. It is worth noting that the e-book recommended by users to predict interest is calculated using formulas on the cosine similarity matrix W calculated by this algorithm. In addition, the user's favorite e-book is also required as input parameters during calculation. The recommended similar e-book is to use the string similarity matrix W for statistics directly. This means that the above two recommendations need to complete the calculation of the co-occurrence matrix of the e-book and the cosine similarity matrix of the e-book. Because the above two matrices are computationally large and all data is required for each calculation, it is set to be performed regularly by the administrator.
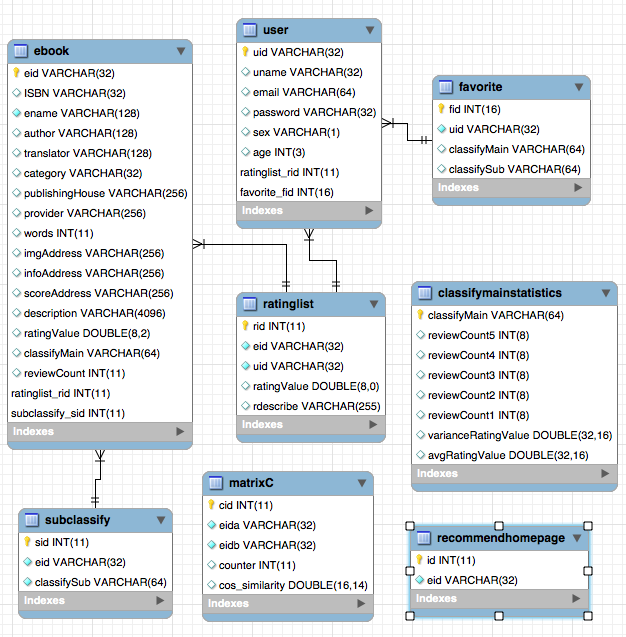
Symbol → indicates that the class is a regular manual operation of modules

There are two main steps for the collaborative filtering algorithm based on items:
Suppose N(i) is the number of users who like item i. N(i)⋂N(j) represents the number of users who like item i item j at the same time. Then the similarity between item i and item j is:
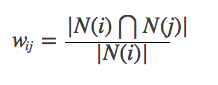
However, the above formula has a defect: when item j is a very popular product and everyone likes it, then wij will be very close to 1, that is, the above formula will make many items have a great similarity to popular products, so you can improve the formula:
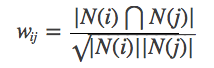
Create a list of user items inverted (suppose uppercase letters represent users, lowercase letters represent items):

Calculate the co-occurrence matrix C (the co-occurrence matrix C represents the number of users who like two items at the same time, and is calculated based on the user item inversion table):
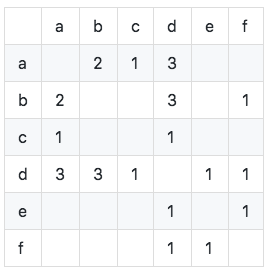
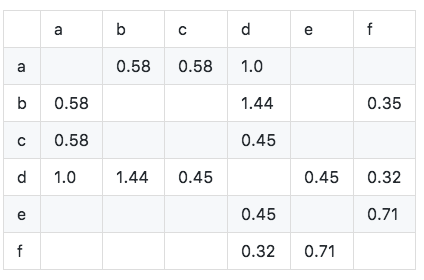
As shown in the figure, we can see that the diagonal elements of the co-occurrence matrix are all 0 and are real symmetric sparse matrices. The algorithm is implemented as follows:
com.statistics.ItemCollaborationFilter
/**
* 计算共现矩阵C
*/
private void computerMatrixC (){
// 建立用户物品倒排表
// 若用户对物品评分大于等于4则认为喜欢(出现)
List < User > allUser = userDao . queryAllUser ();
for ( int i = 0 ; i < allUser . size (); i ++){ // 遍历全部用户
// 获取一个用户的评分列表中>=4的评分记录
List < RatingList > likeList = ratingListDao . selectRatingListByUidAndRatingValue ( allUser . get ( i ). getUid (), 4 );
if ( likeList . size () <= 1 ){ // 若用户只喜欢一本或不喜欢任何图书
continue ;
}
for ( int j = 0 ; j < likeList . size (); j ++){ // 计算likeList中两两出现的图书并写入同现矩阵C
for ( int k = j + 1 ; k < likeList . size (); k ++){
int a = Integer . valueOf ( likeList . get ( j ). getEid ());
int b = Integer . valueOf ( likeList . get ( k ). getEid ());
// 生成key
String key = null ;
if ( a < b ){
key = a + "," + b ;
} else {
key = b + "," + a ;
}
// 检查key是否已经存在
if ( this . matrixC . get ( key ) != null ){
int value = this . matrixC . get ( key );
this . matrixC . put ( key , value + 1 );
} else {
this . matrixC . put ( key , 1 );
}
}
}
System . out . println ( "[" + df . format ( new Date ())+ "]" + "[已完成" + i + ",共" + allUser . size ()+ "]:用户uid=" + allUser . get ( i ). getUid ()+ "的记录以计算完成,共" + likeList . size ()+ "本图书" );
}
}The number of times each item appears is:

Calculate the cosine similarity matrix W: The cosine similarity matrix can be obtained using the improved formula.
The algorithm is implemented as follows:
com.statistics.ItemCollaborationFilter
/**
* 计算余弦相似度矩阵W
* 计算方法:
* 使用矩阵C的每个value作为分子,key中的两个图书的喜欢人数的积开根号作为分母
*/
private Double computerMatrixW ( String eida , String eidb , int value ){
DecimalFormat df = new DecimalFormat ( "#.##" );
// 查询每个图书有多少人喜欢
try {
Statement statemenet = conn . createStatement ();
ResultSet rs = statemenet . executeQuery ( "select count(rid) from ratinglist where eid = '" + eida + "' and ratingValue >= 4;" );
rs . next ();
int likeANum = rs . getInt ( "count(rid)" );
rs = statemenet . executeQuery ( "select count(rid) from ratinglist where eid = '" + eidb + "' and ratingValue >= 4;" );
rs . next ();
int likeBNum = rs . getInt ( "count(rid)" );
if ( likeANum == 0 )
likeANum = 1 ;
if ( likeBNum == 0 )
likeBNum = 1 ;
// 开始计算
Double answer = value * 1.0 / Math . sqrt ( likeANum * likeBNum );
// 精确到小数点后两位
Double result = Double . parseDouble ( df . format ( answer ));
// 返回计算结果
return result ;
} catch ( SQLException e ) {
e . printStackTrace ();
}
return null ;
}What item is ultimately recommended is determined by predicting interest.
Item j predicts interest = interest of item i that the user likes × similarity between item i and item j.
For example: a user likes items a, b, and c. Their interest is 1, 2 and 2 respectively. Then the predicted interest of items c, d, e, and f are:
Therefore, item d should be recommended to the user. The algorithm is implemented as follows:
@ Override
public List < EBook > userRecommendedList ( String uid ) {
// 获取用户喜爱图书列表
List < RatingList > likeList = this . ratingListDao . selectRatingListByUidAndRatingValue ( uid , 4 );
// debug
System . out . println ( "uid=" + uid + "用户喜爱图书列表" );
for ( RatingList r : likeList ){
System . out . println ( r . getEid ()+ "," + r . getRatingValue ());
}
System . out . println ( "likeList.size=" + likeList . size ());
// 定义计算用矩阵
List < Item > matrix = new ArrayList <>();
// 将用户喜爱的图书作为矩阵的列
// 将与用户喜爱的图书同现的图书作为矩阵的行
// 建立工作矩阵
for ( int i = 0 ; i < likeList . size (); i ++){ // 遍历用户喜爱的图书
RatingList temp = likeList . get ( i );
// 获取同现图书
List < MatrixC > itemList = this . matrixCDao . selectMatrixCByEidAOrEidB ( temp . getEid (), temp . getEid ());
for ( int j = 0 ; j < itemList . size (); j ++){
MatrixC c = itemList . get ( j );
// 从matrixC的key中选出同现图书的eid
String sEid = null ;
if ( c . getEida (). equals ( temp . getEid ())){
sEid = c . getEidb ();
} else {
sEid = c . getEida ();
}
// 在行中查询同现图书是否存在
if ( matrix . indexOf ( sEid ) == - 1 ){ // 若列中不存在
double [] col = new double [ likeList . size ()];
// 将同现图书所在行对应喜爱图书的数组值设为对应的余弦相似度*用户喜爱程度(4分为1,5分为2)
col [ likeList . indexOf ( temp )] = c . getCos_similarity ()*( temp . getRatingValue ()- 3 );
matrix . add ( new Item ( sEid , col )); // 增加行
} else { // 若列中存在
// 则将同现图书所在行对应喜爱图书的数组值设为对应的余弦相似度*用户喜爱程度(4分为1,5分为2)
matrix . get ( matrix . indexOf ( sEid )). col [ likeList . indexOf ( temp )] = c . getCos_similarity ()*( temp . getRatingValue ()- 3 );
}
}
}
// 计算预测兴趣度
for ( int i = 0 ; i < matrix . size (); i ++){
Item item = matrix . get ( i );
double interestValue = 0 ;
for ( int j = 0 ; j < item . col . length ; j ++){
interestValue += item . col [ j ];
}
matrix . get ( i ). interestValue = interestValue ;
}
// 根据预测兴趣度进行排序
Collections . sort ( matrix );
// 返回推荐图书列表
List < EBook > resultList = new ArrayList <>();
for ( int i = 0 ; i < matrix . size () && i < 20 ; i ++){ // 返回排前10的书
if ( matrix . get ( i ). interestValue > 0 ){
EBook eBook = this . eBookDao . queryEBookByEid ( matrix . get ( i ). eid );
resultList . add ( eBook );
// debug
System . out . println ( matrix . get ( i ). eid + "," + eBook . getEname ()+ ",interestValue=" + matrix . get ( i ). interestValue );
}
}
return EBookServiceImpl . initEBookImgAddress ( resultList );
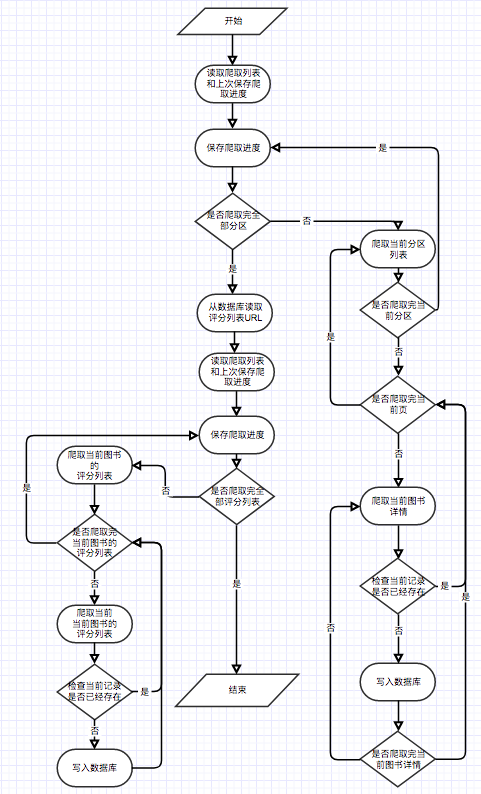
}The recommended module uses the data crawled by the crawler as input to output the calculation results into the matrixC table. The entire calculation process is divided into 2 stages. The first stage calculates the co-occurrence matrix C. The second stage calculates the cosine similarity w of the e-books that appear in pairs. For the recommended function based on user predicted interest, because the user likes the real-time and total calculation amount of e-book data is too large, the user will use real-time calculations when accessing the page. After multiple tests, the average waiting time of the user is within an acceptable range.
Because Douban movie web page upgrade has added anti-crawling measures, data used to run the recommended algorithm is provided here.