
Randomisierte Phase -II -Onkologieversuche mit Bernoulli -Ergebnissen
PH2RAND bietet Funktionen zur Unterstützung des Designs randomisierter Vergleichsphase -II -Onkologieversuche, die davon ausgehen, dass ihre primäre Ergebnisvariable Bernoulli verteilt ist. Insbesondere wird die Unterstützung (a) eine Stichprobengröße berechnet, wenn eines von mehreren veröffentlichten Entwürfen verwendet wird (Jung, 2008; Jung und Sargent, 2014; Kepner, 2010; Litwin et al ., 2017, Shan et al.
Sie können die neueste Entwicklungsversion von PH2RAND installieren, die bei GitHub erhältlich ist, mit
devtools :: install_github( " mjg211/ph2rand " )Ein einführendes Beispiel für die Verwendung der Kernfunktionalität des Pakets finden Sie unten. Weitere Hilfe finden Sie im Paket Vignetten oder senden Sie eine E -Mail an [email protected].
Wir zeigen die Funktionalität für zweistufige Designs, wobei der Ansatz für einstufige Designs ähnlich ist. Suchen Sie zunächst ein zweistufiges Design von Jung (2008) für die Standardparameter
des_jung <- des_two_stage()Untersuchen Sie dann die erforderliche Probengröße in jedem Arm in jeder Phase
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17Schauen Sie sich als nächstes die wichtigsten Betriebsmerkmale an
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Vergleichen Sie dies mit dem äquivalenten Design von Litwin et al. (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Nun dazu von Shan (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Und schließlich das von Jung und Sargent (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Anschließend finden wir die Terminalpunkte eines dieser Entwürfe sowie ihre Wahrscheinlichkeitsmassenfunktionen und Betriebsmerkmale für echte Antwortraten. Betrachten Sie beispielsweise zwei Szenarien, die von angegeben wurden
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))Ermitteln Sie dann die Terminalpunkte, Wahrscheinlichkeitsmassenfunktionen und Betriebsmerkmale (sowohl analytisch als auch über Simulation) des Jung (2008) -Dsigns mit
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Schließlich können wir verschiedene Faktoren in Bezug auf die Designs zeichnen. Zeichnen Sie beispielsweise die Terminalpunkte des Jung (2008) -Desende (mit ihren zugehörigen Entscheidungen) zusammen mit der Wahrscheinlichkeit, die Nullhypothese abzulehnen, wenn die Reaktionswahrscheinlichkeiten in den beiden Armen gleich sind oder wenn die Differenz der Reaktionswahrscheinlichkeiten der gewählte Behandlungseffekt ist
plot( des_jung )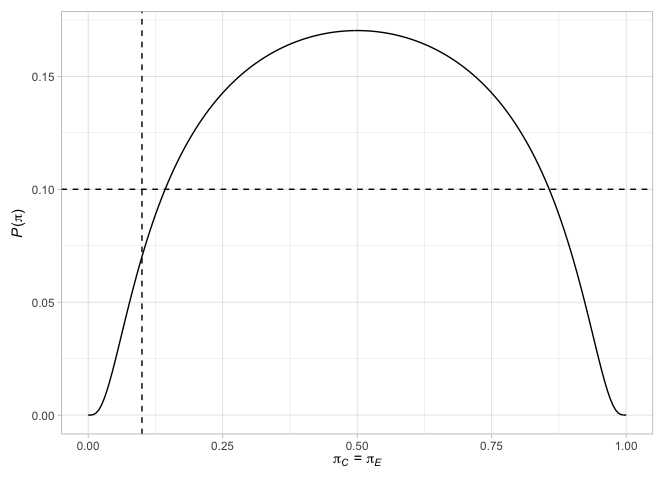
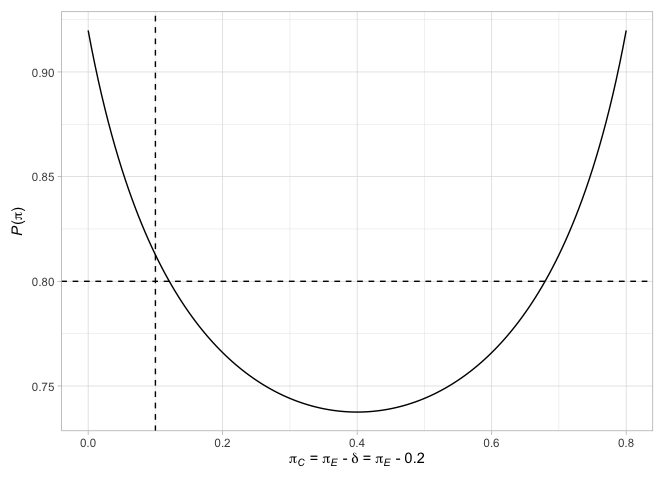
Weitere Informationen finden Sie in den Paketvignetten.
Jung SH (2008) Randomisierte Phase -II -Studien mit einer prospektiven Kontrolle. STAT MED 27 (4): 568–83. Doi: 10.1002/sim.2961. PMID: 17573688.
Jung SH, Sargent DJ (2014) Randomisierte klinische Phase -II -Studien. J Biopharm STAT 24 (4): 802–16. Doi: 10.1080/10543406.2014.901343. PMID: 24697589.
Kepner JL (2010) über Gruppen -sequentielle Designs, die zwei Binomialanteile vergleichen. J Biopharm STAT 20 (1): 145–59. Doi: 10.1080/10543400903280621. PMID: 20077254.
Litwin S, Basickes S, Ross EA (2017) Binär-Phase-2-Versuche mit zwei Stichproben mit niedrigem Typ I-Fehler und niedriger Stichprobengröße. STAT MED 36 (9): 1383–94. Doi: 10.1002/sim.7226. PMID: 28118686.
Shan G, MA C, Hutson AD, Wilding GE (2013) Randomisierte zweistufige klinische Studienentwürfe in der Phase II, die auf dem genauen Barnard-Test basiert. J Biopharm STAT 23 (5): 1081–90. Doi: 10.1080/10543406.2013.813525. PMID: 23957517.