
การทดลองมะเร็งระยะที่สองแบบสุ่มด้วยผลลัพธ์ของ Bernoulli
PH2RAND ให้ฟังก์ชั่นที่จะช่วยในการออกแบบการทดลองด้านเนื้องอกวิทยาแบบสุ่มแบบสุ่มซึ่งถือว่าตัวแปรผลลัพธ์หลักของพวกเขาคือ Bernoulli กระจาย โดยเฉพาะการสนับสนุนมีให้กับ (a) ทำการคำนวณขนาดตัวอย่างเมื่อใช้หนึ่งในการออกแบบที่ตีพิมพ์หลายครั้ง (Jung, 2008; Jung and Sargent, 2014; Kepner, 2010; Litwin et al , 2017, Shan et al , 2013), (b) ประเมินลักษณะการทำงานของการออกแบบที่กำหนด
คุณสามารถติดตั้ง Ph2Rand เวอร์ชันการพัฒนาล่าสุดที่มีให้จาก GitHub ด้วย
devtools :: install_github( " mjg211/ph2rand " )ตัวอย่างเบื้องต้นของวิธีการใช้ประโยชน์จากฟังก์ชันการทำงานหลักของแพ็คเกจสามารถดูได้ด้านล่าง สำหรับความช่วยเหลือเพิ่มเติมโปรดดู Vignettes หรืออีเมล [email protected]
เราแสดงให้เห็นถึงฟังก์ชั่นสำหรับการออกแบบสองขั้นตอนด้วยวิธีการสำหรับการออกแบบขั้นตอนเดียวที่คล้ายกัน ก่อนอื่นค้นหาการออกแบบสองขั้นตอนจาก Jung (2008) สำหรับพารามิเตอร์เริ่มต้น
des_jung <- des_two_stage()จากนั้นตรวจสอบขนาดตัวอย่างที่ต้องการในแต่ละแขนในแต่ละขั้นตอน
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17จากนั้นดูที่ลักษณะการทำงานที่สำคัญ
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>เปรียบเทียบสิ่งนี้กับการออกแบบที่เทียบเท่าจาก Litwin et al (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>ตอนนี้จาก Shan (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>และในที่สุดก็จากจองและซาร์เจนท์ (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>จากนั้นเราสามารถค้นหาจุดเทอร์มินัลของการออกแบบเหล่านี้ได้อย่างง่ายดายพร้อมกับฟังก์ชั่นมวลความน่าจะเป็นและลักษณะการทำงานสำหรับอัตราการตอบสนองที่แท้จริง ตัวอย่างเช่นพิจารณาสองสถานการณ์ที่กำหนดโดย
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))จากนั้นค้นหาจุดเทอร์มินัลฟังก์ชั่นมวลความน่าจะเป็นและลักษณะการทำงาน (ทั้งการวิเคราะห์และผ่านการจำลอง) ของการออกแบบ Jung (2008) ด้วย
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>ในที่สุดเราสามารถพล็อตปัจจัยต่าง ๆ ที่เกี่ยวข้องกับการออกแบบ ตัวอย่างเช่นพล็อตจุดเทอร์มินัลของ Jung (2008) การออกแบบ (ด้วยการตัดสินใจที่เกี่ยวข้อง) พร้อมกับความน่าจะเป็นที่จะปฏิเสธสมมติฐานว่างเมื่อความน่าจะเป็นในการตอบสนองเท่ากันในสองแขนหรือเมื่อความแตกต่างของความน่าจะเป็นในการตอบสนองคือผลการรักษาที่เลือก
plot( des_jung )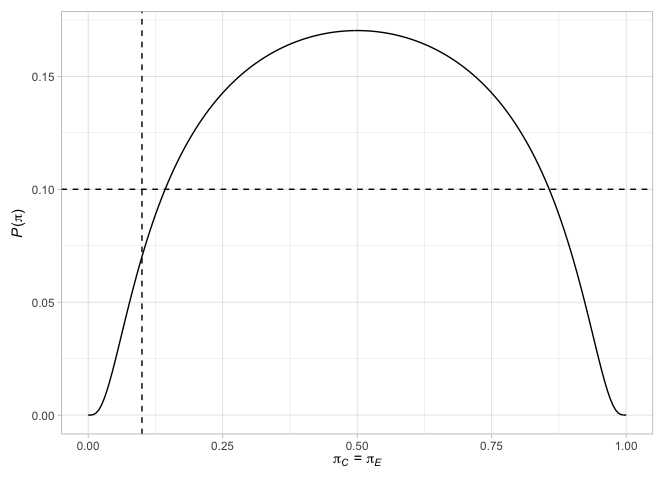
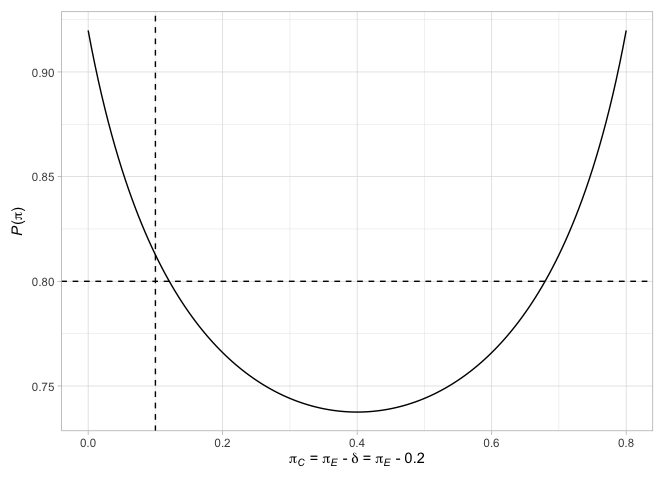
ดูบทความสั้น ๆ สำหรับรายละเอียดเพิ่มเติม
Jung SH (2008) การทดลองระยะที่สองแบบสุ่มด้วยการควบคุมที่คาดหวัง Stat Med 27 (4): 568–83 ดอย: 10.1002/sim.2961 PMID: 17573688
Jung SH, Sargent DJ (2014) การทดลองทางคลินิกระยะที่สองแบบสุ่ม J Biopharm Stat 24 (4): 802–16 ดอย: 10.1080/10543406.2014.901343 PMID: 24697589
Kepner JL (2010) เกี่ยวกับการออกแบบตามลำดับกลุ่มเปรียบเทียบสองสัดส่วนทวินาม J Biopharm Stat 20 (1): 145–59 ดอย: 10.1080/10543400903280621 PMID: 20077254
Litwin S, Basickes S, Ross EA (2017) การทดลองแบบไบนารีสองตัวอย่างสองตัวอย่างที่มีข้อผิดพลาดประเภทต่ำและขนาดตัวอย่างต่ำ Stat Med 36 (9): 1383–94 ดอย: 10.1002/sim.7226 PMID: 28118686
Shan G, Ma C, Hutson AD, Wilding GE (2013) สุ่มการออกแบบการทดลองทางคลินิกระยะที่สองระยะที่สองจากการทดสอบที่แน่นอนของบาร์นาร์ด J Biopharm Stat 23 (5): 1081–90 ดอย: 10.1080/10543406.2013.813525 PMID: 23957517