
ベルヌーリの結果を伴うランダム化第II相腫瘍学試験
PH2RANDは、主要な結果変数がベルヌーリ分布であると仮定する、ランダム化比較フェーズII腫瘍学試験の設計を支援する機能を提供します。具体的には、(a)いくつかの公開されたデザインのいずれかを使用する場合のサンプルサイズの計算を実行するためにサポートが提供されます(Jung、2008; Jung and Sargent、2014; Kepner、2010; Litwin et al 、2017、Shan et al 、2013)、(b)特定のデザインの動作特性を評価します(分析的および介して、実質的なプロットを生成します。
Githubから入手可能なPh2Randの最新の開発バージョンをインストールできます。
devtools :: install_github( " mjg211/ph2rand " )パッケージのコア機能を使用する方法の紹介例を以下に示します。さらにヘルプについては、パッケージビネットまたはメール[email protected]にメールしてください。
2段階の設計の機能を実証し、単一段階のデザインのアプローチが似ています。まず、デフォルトのパラメーターについては、Jung(2008)から2段階のデザインを見つけます
des_jung <- des_two_stage()次に、各腕の各段階で必要なサンプルサイズを調べます
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17次に、その主要な動作特性を見てください
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Litwin et al (2017)の同等のデザインとこれを比較してください
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>今、シャン(2013)から
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>そして最後に、Jung and Sargent(2014)から
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>その後、これらの設計のいずれかの端子ポイントと、その確率の質量関数と真の応答率の動作特性を容易に見つけることができます。たとえば、次の2つのシナリオを検討してください
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))次に、Jung(2008)の設計の端子点、確率質量関数、および動作特性(分析的およびシミュレーション経由)を見つけます
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>最後に、デザインに関連するさまざまな要因をプロットできます。たとえば、Jung(2008)設計の端子ポイント(関連する決定を伴う)をプロットし、応答確率が2つの腕で等しい場合、または応答確率の違いが選択された治療効果である場合に帰無仮説を拒否する確率とともにプロットします。
plot( des_jung )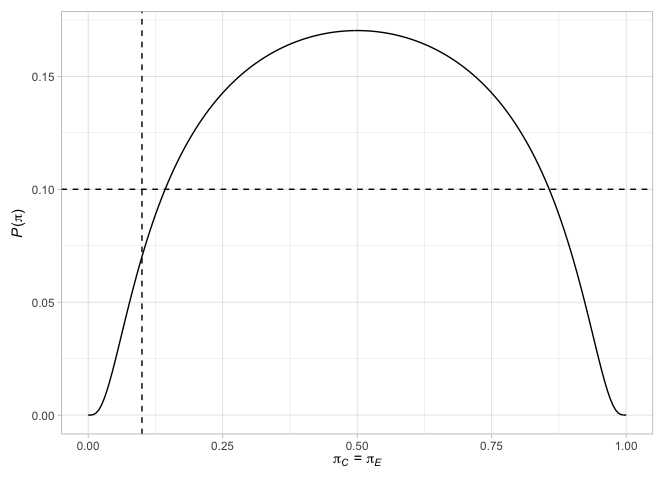
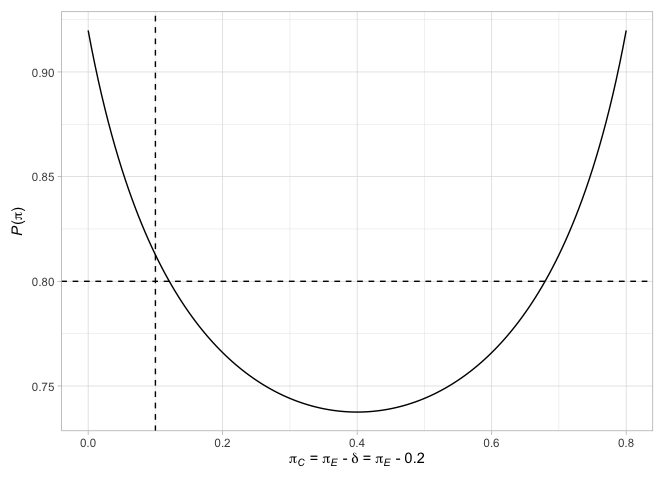
詳細については、パッケージビネットを参照してください。
Jung SH(2008)将来のコントロールを伴う第II相試験を無作為化。 Stat Med 27(4):568–83。 doi:10.1002/sim.2961。 PMID:17573688。
Jung SH、Sargent DJ(2014)無作為化第II相臨床試験。 J Biopharm Stat 24(4):802–16。 doi:10.1080/10543406.2014.901343。 PMID:24697589。
Kepner JL(2010)2つの二項式の割合を比較するグループシーケンシャルデザイン。 J Biopharm Stat 20(1):145–59。 doi:10.1080/10543400903280621。 PMID:20077254。
Litwin S、Basickes S、Ross EA(2017)タイプIエラーが低く、サンプルサイズが低い2サンプルバイナリフェーズ2試験。 Stat Med 36(9):1383–94。 doi:10.1002/sim.7226。 PMID:28118686。
Shan G、Ma C、Hutson AD、Wilding GE(2013)Barnardの正確なテストに基づいて、2段階の第II相臨床試験設計を無作為化しました。 J Biopharm Stat 23(5):1081–90。 doi:10.1080/10543406.2013.813525。 PMID:23957517。