
Ensayos aleatorizados de oncología de la Fase II con resultados de Bernoulli
PH2RAND proporciona funciones para ayudar con el diseño de ensayos de oncología de fase II comparativos aleatorios que suponen que su variable de resultado primaria está distribuida por Bernoulli. Específicamente, el soporte se proporciona a (a) realizar un cálculo de tamaño de muestra cuando se usa uno de varios diseños publicados (Jung, 2008; Jung y Sargent, 2014; Kepner, 2010; Litwin et al , 2017, Shan et al , 2013), (b) evalúan las características operativas de un diseño dado (tanto analíticamente como por simulación) y ((c) c) gráficos informativos.
Puede instalar la última versión de desarrollo de Ph2Rand , disponible en Github, con
devtools :: install_github( " mjg211/ph2rand " )A continuación se puede encontrar un ejemplo introductorio de cómo hacer uso de la funcionalidad central del paquete. Para obtener más ayuda, consulte el paquete Vignettes o envíe un correo electrónico a [email protected].
Demostramos la funcionalidad para los diseños de dos etapas, con el enfoque de diseños de una sola etapa es similar. Primero, encuentre un diseño de dos etapas de Jung (2008) para los parámetros predeterminados
des_jung <- des_two_stage()Luego examine su tamaño de muestra requerido en cada brazo, en cada etapa
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17A continuación, mire sus características operativas clave
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Compare esto con el diseño equivalente de Litwin et al (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Ahora a eso de Shan (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Y finalmente eso de Jung y Sargent (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Luego podemos encontrar fácilmente los puntos terminales de cualquiera de estos diseños, junto con sus funciones de masa de probabilidad y características operativas para cualquier tasa de respuesta verdadera. Por ejemplo, considere dos escenarios dados por
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))Luego encuentre los puntos terminales, las funciones de masa de probabilidad y las características operativas (tanto analíticamente como mediante simulación) del diseño de Jung (2008) con
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Finalmente, podemos trazar varios factores relacionados con los diseños. Por ejemplo, traza los puntos terminales del diseño de Jung (2008) (con sus decisiones asociadas), junto con la probabilidad de rechazar la hipótesis nula cuando las probabilidades de respuesta son iguales en los dos brazos o cuando la diferencia en las probabilidades de respuesta es el efecto de tratamiento elegido
plot( des_jung )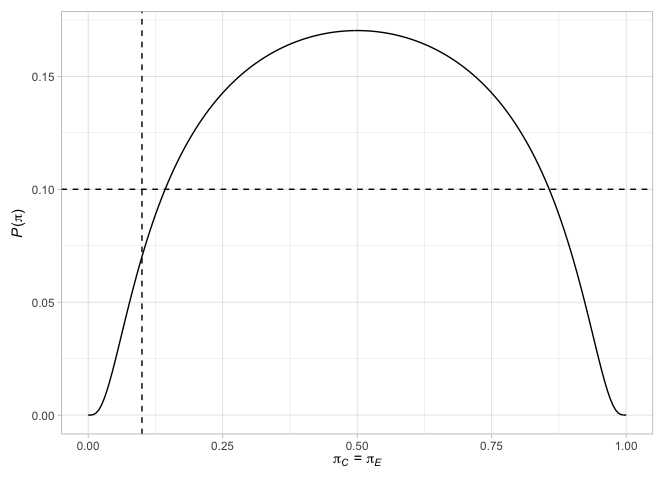
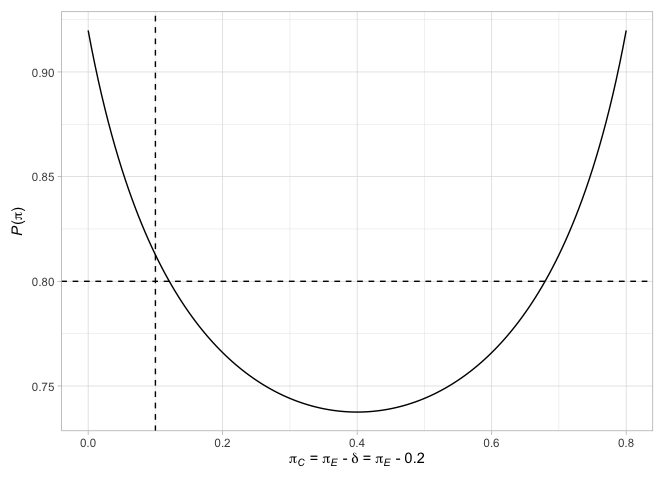
Consulte el paquete de viñetas para más detalles.
Jung SH (2008) ensayos aleatorios de fase II con un control prospectivo. Stat Med 27 (4): 568–83. Doi: 10.1002/sim.2961. PMID: 17573688.
Jung SH, Sargent DJ (2014) Ensayos clínicos aleatorios de fase II. J Biopharm Stat 24 (4): 802–16. Doi: 10.1080/10543406.2014.901343. PMID: 24697589.
Kepner JL (2010) en diseños secuenciales grupales que comparan dos proporciones binomiales. J Biopharm Stat 20 (1): 145–59. Doi: 10.1080/10543400903280621. PMID: 20077254.
Litwin S, Basickes S, Ross EA (2017) Ensayos binarios de fase 2 de dos muestras con bajo error de tipo I y bajo tamaño de muestra. Stat Med 36 (9): 1383–94. Doi: 10.1002/sim.7226. PMID: 28118686.
Shan G, Ma C, Hutson AD, Wilding GE (2013) Diseños aleatorizados de ensayos clínicos de fase II de dos etapas basados en la prueba exacta de Barnard. J Biopharm Stat 23 (5): 1081–90. Doi: 10.1080/10543406.2013.813525. PMID: 23957517.