
Bernoulli 결과를 이용한 무작위 2 상 종양학 시험
PH2Rand는 그들의 주요 결과 변수가 Bernoulli 분포라고 가정하는 무작위 비교 2 단계 종양학 시험의 설계를 지원하는 기능을 제공합니다. 구체적으로, (a) 여러 출판 된 디자인 중 하나를 사용할 때 (a) 샘플 크기 계산을 수행하기위한 지원이 제공됩니다 (Jung, 2008; Jung and Sargent, 2014; Kepner, 2010; Litwin et al , 2017, Shan et al , 2013), (b) 주어진 디자인의 작동 특성 (분석적 및 시뮬레이션을 통해), (C)의 정보를 제공합니다.
Github에서 제공하는 Ph2rand 의 최신 개발 버전을 다음과 같이 설치할 수 있습니다.
devtools :: install_github( " mjg211/ph2rand " )패키지의 핵심 기능을 사용하는 방법에 대한 소개 예는 아래에서 찾을 수 있습니다. 추가 도움은 패키지 비네팅 또는 이메일 [email protected]를 참조하십시오.
우리는 단일 단계 디자인에 대한 접근 방식이 비슷한 2 단계 디자인의 기능을 보여줍니다. 먼저 기본 매개 변수에 대한 Jung (2008)에서 2 단계 디자인을 찾으십시오.
des_jung <- des_two_stage()그런 다음 각 단계에서 필요한 샘플 크기를 검사하십시오.
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17다음으로 주요 작동 특성을 살펴보십시오
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>이것을 Litwin et al (2017)의 동등한 설계와 비교하십시오.
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>이제 Shan (2013)에서
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>그리고 마침내 Jung and Sargent (2014)의
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>그런 다음 이러한 설계의 터미널 포인트와 실제 응답 속도에 대한 확률 질량 기능 및 작동 특성과 함께 쉽게 찾을 수 있습니다. 예를 들어, 두 가지 시나리오를 고려하십시오
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))그런 다음 Jung (2008) 디자인의 터미널 포인트, 확률 질량 기능 및 작동 특성 (분석적 및 시뮬레이션을 통해)을 찾으십시오.
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>마지막으로, 우리는 디자인과 관련된 다양한 요소를 그릴 수 있습니다. 예를 들어, Jung (2008) 설계의 터미널 포인트 (관련 결정과 함께)와 반응 확률이 두 팔에서 동일 할 때 귀무 가설을 거부 할 확률과 함께 또는 응답 확률의 차이가 선택된 치료 효과 일 때
plot( des_jung )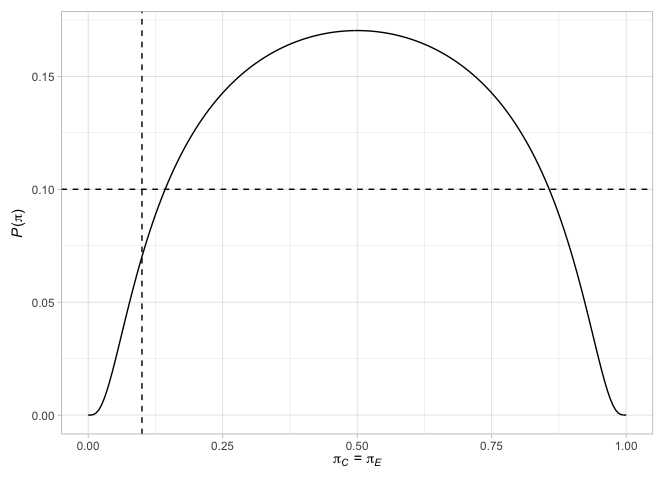
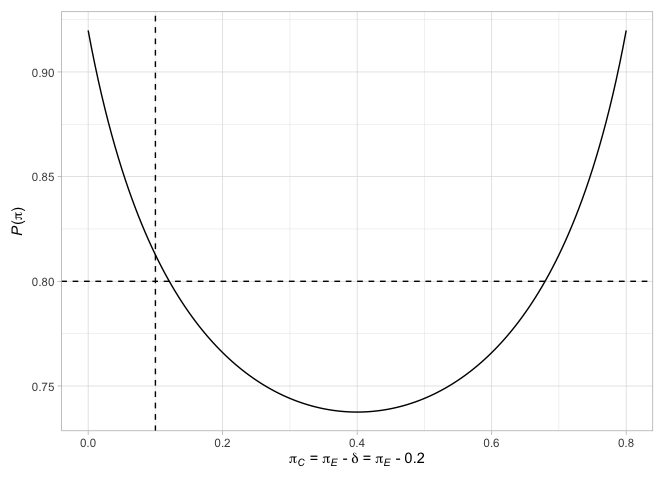
자세한 내용은 패키지 비네팅을 참조하십시오.
Jung SH (2008) 전향 적 통제를 가진 무작위 2 상 시험. STAT MED 27 (4) : 568–83. doi : 10.1002/sim.2961. PMID : 17573688.
Jung SH, Sargent DJ (2014) 무작위 2 상 임상 시험. J Biopharm Stat 24 (4) : 802–16. doi : 10.1080/10543406.2014.901343. PMID : 24697589.
Kepner JL (2010)는 두 가지 이항 비율을 비교하는 그룹 순차 디자인에 관한 것입니다. J Biopharm Stat 20 (1) : 145–59. doi : 10.1080/10543400903280621. PMID : 20077254.
Litwin S, Basickes S, Ross EA (2017) 낮은 유형 I 오류 및 낮은 샘플 크기를 갖는 2- 샘플 바이너리 상 2 시험. STAT MED 36 (9) : 1383–94. doi : 10.1002/sim.7226. PMID : 28118686.
Shan G, Ma C, Hutson AD, Wilding GE (2013) Barnard의 정확한 테스트를 기반으로 2 단계 2 단계 2 단계 임상 시험 설계. J Biopharm Stat 23 (5) : 1081–90. doi : 10.1080/10543406.2013.813525. PMID : 23957517.