
Uji Onkologi Tahap II Acak Dengan Hasil Bernoulli
PH2RAND menyediakan fungsi untuk membantu desain uji onkologi Fase II komparatif acak yang mengasumsikan variabel hasil utama mereka didistribusikan Bernoulli. Secara khusus, dukungan diberikan kepada (a) melakukan perhitungan ukuran sampel saat menggunakan salah satu dari beberapa desain yang diterbitkan (Jung, 2008; Jung dan Sargent, 2014; Kepner, 2010; Litwin et al , 2017, Shan et al , 2013), (b) mengevaluasi karakteristik operasi dari desain yang diberikan (baik secara analitik maupun melalui simulasi), dan (c).
Anda dapat menginstal versi pengembangan terbaru Ph2Rand , tersedia dari GitHub, dengan
devtools :: install_github( " mjg211/ph2rand " )Contoh pengantar tentang cara memanfaatkan fungsi inti paket dapat ditemukan di bawah. Untuk bantuan lebih lanjut, silakan lihat paket sketsa atau email [email protected].
Kami menunjukkan fungsionalitas untuk desain dua tahap, dengan pendekatan untuk desain tahap tunggal serupa. Pertama, temukan desain dua tahap dari Jung (2008) untuk parameter default
des_jung <- des_two_stage()Kemudian periksa ukuran sampel yang diperlukan di setiap lengan, di setiap tahap
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17Selanjutnya, lihat karakteristik operasi utamanya
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Bandingkan ini dengan desain yang setara dari Litwin et al (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Sekarang untuk itu dari Shan (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Dan akhirnya dari Jung dan Sargent (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Kami kemudian dapat dengan mudah menemukan titik -titik terminal dari salah satu dari desain ini, bersama dengan fungsi massa probabilitas dan karakteristik operasi untuk setiap tingkat respons sejati. Misalnya, pertimbangkan dua skenario yang diberikan oleh
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))Kemudian temukan titik terminal, fungsi massa probabilitas, dan karakteristik operasi (baik secara analitik maupun melalui simulasi) dari desain Jung (2008) dengan
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
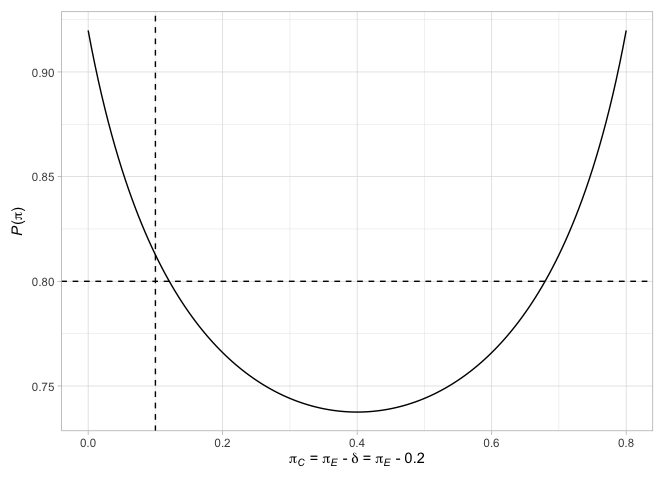
# > # N` <int>Akhirnya, kita dapat merencanakan berbagai faktor yang berkaitan dengan desain. Sebagai contoh, plot titik -titik terminal dari desain Jung (2008) (dengan keputusan terkait), bersama dengan probabilitas menolak hipotesis nol ketika probabilitas respons sama pada kedua lengan atau ketika perbedaan probabilitas respons adalah efek pengobatan yang dipilih
plot( des_jung )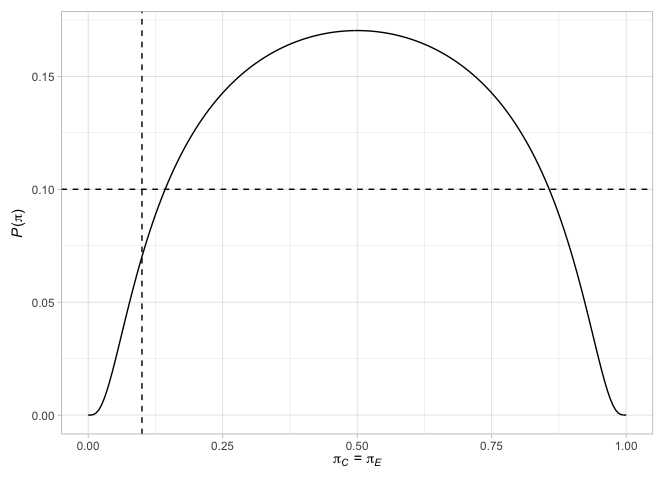
Lihat sketsa paket untuk perincian lebih lanjut.
Jung SH (2008) Uji coba Fase II secara acak dengan kontrol prospektif. Stat Med 27 (4): 568–83. Doi: 10.1002/sim.2961. PMID: 17573688.
Jung SH, Sargent DJ (2014) Uji klinis Fase II secara acak. J Biopharm Stat 24 (4): 802–16. Doi: 10.1080/10543406.2014.901343. PMID: 24697589.
Kepner JL (2010) pada desain sekuensial grup yang membandingkan dua proporsi binomial. J Biopharm Stat 20 (1): 145–59. Doi: 10.1080/10543400903280621. PMID: 20077254.
Litwin S, Basickes S, Ross EA (2017) Uji coba biner dua sampel fase 2 dengan kesalahan tipe I rendah dan ukuran sampel rendah. Stat Med 36 (9): 1383–94. Doi: 10.1002/sim.7226. PMID: 28118686.
Shan G, Ma C, Hutson AD, Wilding GE (2013) Desain uji klinis fase II dua tahap secara acak berdasarkan tes eksak Barnard. J Biopharm Stat 23 (5): 1081–90. Doi: 10.1080/10543406.2013.813525. PMID: 23957517.