
Essais d'oncologie randomisés de phase II avec les résultats de Bernoulli
PH2RAND fournit des fonctions pour aider à la conception d'essais d'oncologie comparative randomisés de phase II qui supposent que leur principale variable de résultat est distribuée par Bernoulli. Plus précisément, le support est fourni pour (a) effectuer un calcul de la taille de l'échantillon lors de l'utilisation de l'une des nombreuses conceptions publiées (Jung, 2008; Jung et Sargent, 2014; Kepner, 2010; Litwin et al , 2017, Shan et al , 2013), (b) évaluer les caractéristiques de fonctionnement d'une conception donnée (à la fois analytiquement et via la simulation) et (C) produisent des places informatives.
Vous pouvez installer la dernière version de développement de Ph2Rand , disponible auprès de GitHub, avec
devtools :: install_github( " mjg211/ph2rand " )Un exemple d'introduction de la façon d'utiliser la fonctionnalité principale du package peut être trouvé ci-dessous. Pour plus d'aide, veuillez consulter les vignettes du package ou envoyer un courriel à [email protected].
Nous démontrons les fonctionnalités des conceptions en deux étapes, l'approche pour les conceptions à un stade étant similaire. Tout d'abord, trouvez une conception en deux étapes de Jung (2008) pour les paramètres par défaut
des_jung <- des_two_stage()Ensuite, examinez sa taille d'échantillon requise dans chaque bras, à chaque étape
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17Ensuite, regardez ses caractéristiques de fonctionnement clés
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Comparez cela à la conception équivalente de Litwin et al (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Maintenant à cela de Shan (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Et enfin cela de Jung et Sargent (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Nous pouvons alors facilement trouver les points terminaux de l'une de ces conceptions, ainsi que leurs fonctions de masse de probabilité et leurs caractéristiques de fonctionnement pour tout taux de réponse réel. Par exemple, considérez deux scénarios donnés par
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))Trouvez ensuite les points terminaux, les fonctions de masse de probabilité et les caractéristiques de fonctionnement (à la fois analytiquement et via la simulation) de la conception de Jung (2008) avec
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Enfin, nous pouvons tracer divers facteurs relatifs aux conceptions. Par exemple, tracer les points terminaux de la conception de Jung (2008) (avec leurs décisions associées), ainsi que la probabilité de rejeter l'hypothèse nulle lorsque les probabilités de réponse sont égales dans les deux bras ou lorsque la différence dans les probabilités de réponse est l'effet de traitement choisi
plot( des_jung )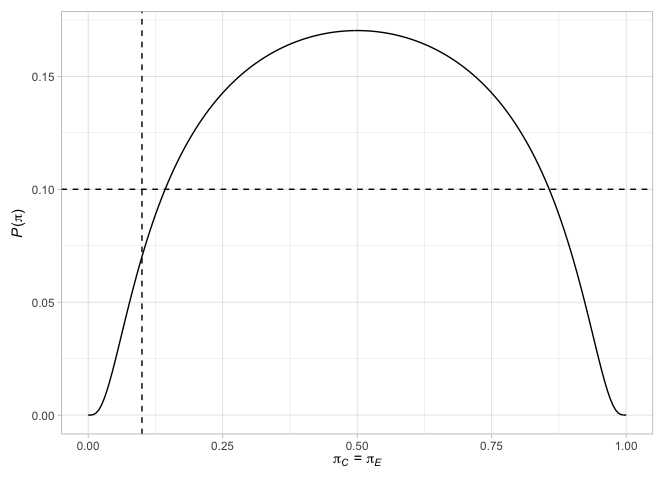
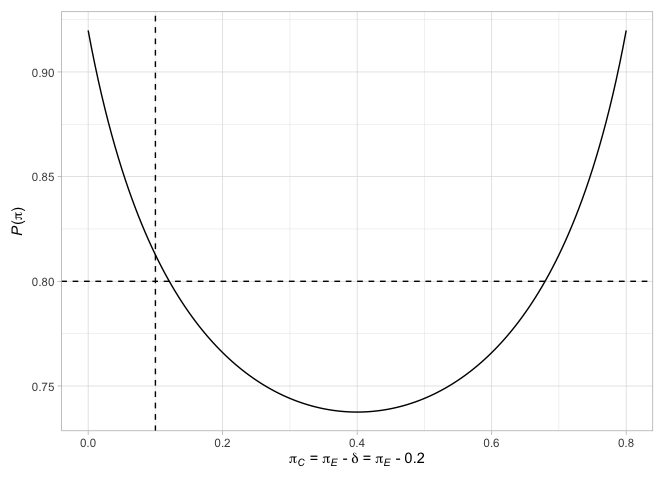
Voir les vignettes du package pour plus de détails.
Jung SH (2008) essais randomisés de phase II avec un contrôle prospectif. Stat Med 27 (4): 568–83. Doi: 10.1002 / sim.2961. PMID: 17573688.
Jung SH, Sargent DJ (2014) essais cliniques randomisés de phase II. J Biopharm Stat 24 (4): 802–16. Doi: 10.1080 / 10543406.2014.901343. PMID: 24697589.
Kepner JL (2010) sur des conceptions séquentielles de groupe comparant deux proportions binomiales. J Biopharm Stat 20 (1): 145–59. Doi: 10.1080 / 10543400903280621. PMID: 20077254.
Litwin S, Basickes S, Ross EA (2017) Essais de phase binaire à deux échantillons 2 avec une erreur de type I faible et une faible taille d'échantillon. Stat Med 36 (9): 1383–94. Doi: 10.1002 / sim.7226. PMID: 28118686.
Shan G, Ma C, Hutson AD, Wilding GE (2013) Randomisé des conceptions d'essais cliniques de phase II en deux étapes basés sur le test exact de Barnard. J Biopharm Stat 23 (5): 1081–90. Doi: 10.1080 / 10543406.2013.813525. PMID: 23957517.