
Ensaios de oncologia da Fase II randomizada com resultados de Bernoulli
O PH2RAND fornece funções para ajudar no projeto de ensaios de oncologia comparativa e randomizada que assumem que sua variável de resultado primário é distribuída em Bernoulli. Especificamente, o suporte é fornecido para (a) realizar um cálculo de tamanho de amostra ao usar um dos vários projetos publicados (Jung, 2008; Jung e Sargent, 2014; Kepner, 2010; Litwin et al , 2017, Shan et al , 2013), (B) avaliar as características de operação de um determinado design (analticamente e via simulação), e (C).
Você pode instalar a versão mais recente de desenvolvimento do PH2Rand , disponível no GitHub, com
devtools :: install_github( " mjg211/ph2rand " )Um exemplo introdutório de como usar a funcionalidade principal do pacote pode ser encontrado abaixo. Para obter mais ajuda, consulte as vinhetas do pacote ou envie um email para [email protected].
Demonstramos a funcionalidade para projetos de dois estágios, com a abordagem para designs de estágio único sendo semelhantes. Primeiro, encontre um design de duas etapas de Jung (2008) para os parâmetros padrão
des_jung <- des_two_stage()Em seguida, examine seu tamanho de amostra necessário em cada braço, em cada estágio
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17Em seguida, veja suas principais características operacionais
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Compare isso com o design equivalente de Litwin et al (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Agora para isso de Shan (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>E finalmente isso de Jung e Sargent (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Podemos então encontrar prontamente os pontos terminais de qualquer um desses projetos, juntamente com suas funções de massa de probabilidade e características operacionais para quaisquer taxas de resposta verdadeiras. Por exemplo, considere dois cenários dados por
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))Em seguida, encontre os pontos terminais, as funções de massa de probabilidade e as características operacionais (analiticamente e via simulação) do design de Jung (2008) com
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>Finalmente, podemos plotar vários fatores relacionados aos projetos. Por exemplo, plote os pontos terminais do projeto de Jung (2008) (com suas decisões associadas), juntamente com a probabilidade de rejeitar a hipótese nula quando as probabilidades de resposta são iguais nos dois braços ou quando a diferença nas probabilidades de resposta é o efeito de tratamento escolhido
plot( des_jung )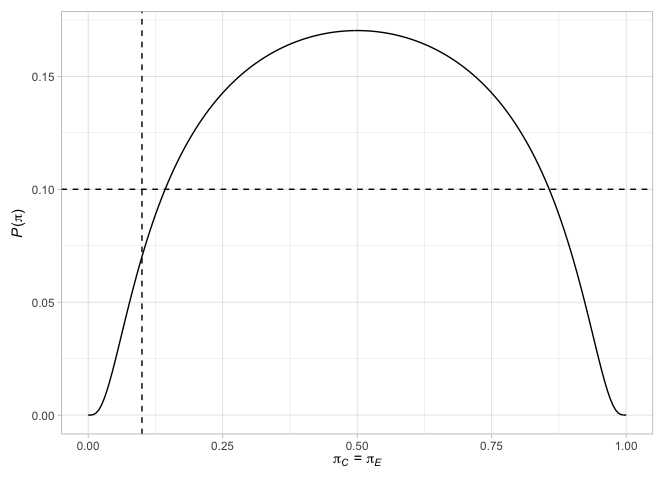
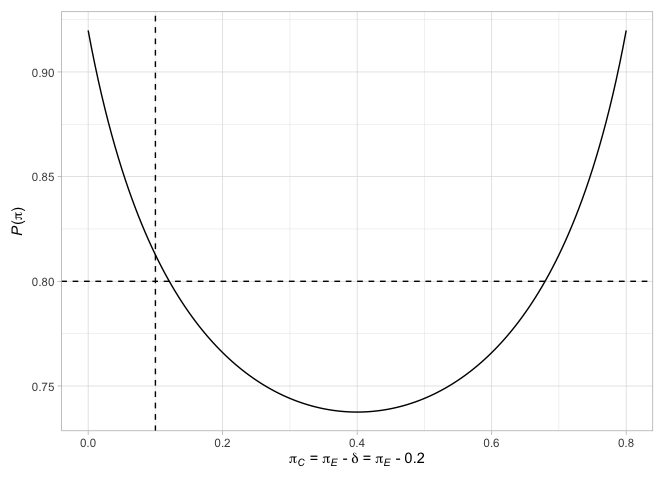
Veja as vinhetas do pacote para obter mais detalhes.
Jung Sh (2008) Ensaios randomizados de fase II com um controle prospectivo. Stat Med 27 (4): 568–83. Doi: 10.1002/sim.2961. PMID: 17573688.
Jung SH, Sargent DJ (2014) Ensaios clínicos randomizados da Fase II. J Biopharm Stat 24 (4): 802–16. Doi: 10.1080/10543406.2014.901343. PMID: 24697589.
Kepner JL (2010) em projetos seqüenciais do grupo comparando duas proporções binomiais. J Biopharm Stat 20 (1): 145–59. Doi: 10.1080/10543400903280621. PMID: 20077254.
Litwin S, Bastices S, Ross EA (2017) Ensaios binários de fase 2 de duas amostras com erro baixo do tipo I e baixo tamanho de amostra. Stat Med 36 (9): 1383–94. Doi: 10.1002/sim.7226. PMID: 28118686.
Shan G, Ma C, Hutson AD, Wilding GE (2013) Projetos randomizados de ensaios clínicos de Fase II de dois estágios com base no teste exato de Barnard. J Biopharm Stat 23 (5): 1081–90. Doi: 10.1080/10543406.2013.813525. PMID: 23957517.