
تجارب الأورام المرحلة الثانية العشوائية مع نتائج برنولي
يوفر PH2RAND وظائف للمساعدة في تصميم تجارب الأورام المقارنة العشوائية التي تفترض أن متغير النتيجة الأولية هو بيرنولي الموزعة. على وجه التحديد ، يتم توفير الدعم إلى (أ) إجراء حساب حجم العينة عند استخدام أحد التصميمات المنشورة العديدة (Jung ، 2008 ؛ Jung and Sargent ، 2014 ؛ Kepner ، 2010 ؛ Litwin et al ، 2017 ، Shan et al ، 2013) ، (ب) تقييم خصائص التشغيل لتصميم معين (سواء تحليليًا أو عبر المحاكاة) ، و (C).
يمكنك تثبيت أحدث إصدار تطوير من ph2rand ، متاح من Github ، مع
devtools :: install_github( " mjg211/ph2rand " )يمكن العثور على مثال تمهيدي على كيفية الاستفادة من الوظائف الأساسية للحزمة أدناه. لمزيد من المساعدة ، يرجى الاطلاع على الحزمة المقالات القصيرة أو البريد الإلكتروني [email protected].
نوضح وظائف التصميمات على مرحلتين ، مع كون نهج التصميمات أحادية المرحلة متشابهة. أولاً ، ابحث عن تصميم على مرحلتين من Jung (2008) للمعلمات الافتراضية
des_jung <- des_two_stage()ثم فحص حجم العينة المطلوب في كل ذراع ، في كل مرحلة
des_jung $ nC
# > [1] 17 17
des_jung $ nE
# > [1] 17 17بعد ذلك ، انظر إلى خصائص التشغيل الرئيسية
des_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>قارن هذا بالتصميم المكافئ من Litwin et al (2017)
des_litwin_et_al <- des_two_stage( type = " sat " ,
nCmax = 20L )
des_litwin_et_al $ nC
# > [1] 10 10
des_litwin_et_al $ nE
# > [1] 10 10
des_litwin_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.100 25.2 8.79 20 0 0.100 0.739
# > 2 0.1 0.3 0.804 36.9 7.20 40 0 0.804 0.153
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>الآن إلى ذلك من شان (2013)
des_shan_et_al <- des_two_stage( type = " barnard " ,
nCmax = 40L )
des_shan_et_al $ nC
# > [1] 17 17
des_shan_et_al $ nE
# > [1] 17 17
des_shan_et_al $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0968 47.0 16.5 34 0 0.0968 0.617
# > 2 0.1 0.3 0.800 64.7 10.1 68 0 0.800 0.0977
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>وأخيرا ذلك من يونغ وسارجنت (2014)
des_jung_sargent <- des_two_stage( type = " fisher " )
des_jung_sargent $ nC
# > [1] 22 22
des_jung_sargent $ nE
# > [1] 22 22
des_jung_sargent $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0530 61.5 21.5 44 0 0.0530 0.602
# > 2 0.1 0.3 0.808 85.2 10.7 88 0 0.808 0.0627
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>يمكننا بعد ذلك العثور على النقاط الطرفية لأي من هذه التصميمات ، إلى جانب وظائف كتلة الاحتمالات وخصائص التشغيل لأي معدلات استجابة حقيقية. على سبيل المثال ، ضع في اعتبارك سيناريوهين قدمهما
pi <- rbind(c( 0.1 , 0.1 ),
c( 0.1 , 0.3 ))ثم ابحث عن نقاط الطرفية ، وظائف كتلة الاحتمالات ، وخصائص التشغيل (سواء تحليليًا أو عبر محاكاة) لتصميم Jung (2008) مع
terminal_jung <- terminal( des_jung )
terminal_jung $ terminal
# > # A tibble: 1,344 x 7
# > xC xE mC mE statistic decision k
# > <int> <int> <int> <int> <int> <fct> <fct>
# > 1 0 0 17 17 0 Do not reject 1
# > 2 0 1 17 17 1 Continue to stage 2 1
# > 3 0 2 17 17 2 Continue to stage 2 1
# > 4 0 3 17 17 3 Continue to stage 2 1
# > 5 0 4 17 17 4 Continue to stage 2 1
# > 6 0 5 17 17 5 Continue to stage 2 1
# > 7 0 6 17 17 6 Continue to stage 2 1
# > 8 0 7 17 17 7 Continue to stage 2 1
# > 9 0 8 17 17 8 Continue to stage 2 1
# > 10 0 9 17 17 9 Continue to stage 2 1
# > # … with 1,334 more rows
pmf_jung <- pmf( des_jung , pi )
pmf_jung $ pmf
# > # A tibble: 2,382 x 10
# > piC piE xC xE mC mE statistic decision k `f(x,m|pi)`
# > <dbl> <dbl> <int> <int> <int> <int> <int> <fct> <fct> <dbl>
# > 1 0.1 0.1 0 0 17 17 0 Do not reject 1 0.0278
# > 2 0.1 0.1 1 0 17 17 -1 Do not reject 1 0.0525
# > 3 0.1 0.1 1 1 17 17 0 Do not reject 1 0.0992
# > 4 0.1 0.1 2 0 17 17 -2 Do not reject 1 0.0467
# > 5 0.1 0.1 2 1 17 17 -1 Do not reject 1 0.0882
# > 6 0.1 0.1 2 2 17 17 0 Do not reject 1 0.0784
# > 7 0.1 0.1 3 0 17 17 -3 Do not reject 1 0.0259
# > 8 0.1 0.1 3 1 17 17 -2 Do not reject 1 0.0490
# > 9 0.1 0.1 3 2 17 17 -1 Do not reject 1 0.0436
# > 10 0.1 0.1 3 3 17 17 0 Do not reject 1 0.0242
# > # … with 2,372 more rows
opchar_jung <- opchar( des_jung , pi )
opchar_jung $ opchar
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0702 47.0 16.5 34 0 0.0702 0.617
# > 2 0.1 0.3 0.813 64.7 10.1 68 0 0.813 0.0972
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>
sim_jung <- sim( des_jung , pi )
sim_jung $ sim
# > # A tibble: 2 x 13
# > piC piE `P(pi)` `ESS(pi)` `SDSS(pi)` `MSS(pi)` `E1(pi)` `E2(pi)` `F1(pi)`
# > <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# > 1 0.1 0.1 0.0727 47.0 16.5 34 0 0.0727 0.617
# > 2 0.1 0.3 0.815 64.7 10.0 68 0 0.815 0.0961
# > # … with 4 more variables: `F2(pi)` <dbl>, `S1(pi)` <dbl>, `S2(pi)` <dbl>, `max
# > # N` <int>أخيرًا ، يمكننا رسم عوامل مختلفة تتعلق بالتصميمات. على سبيل المثال ، ارسم النقاط الطرفية لتصميم Jung (2008) (مع القرارات المرتبطة بها) ، إلى جانب احتمال رفض الفرضية الفارغة عندما تكون احتمالات الاستجابة متساوية في الذراعين أو عندما يكون الفرق في احتمالات الاستجابة هو تأثير العلاج المختار
plot( des_jung )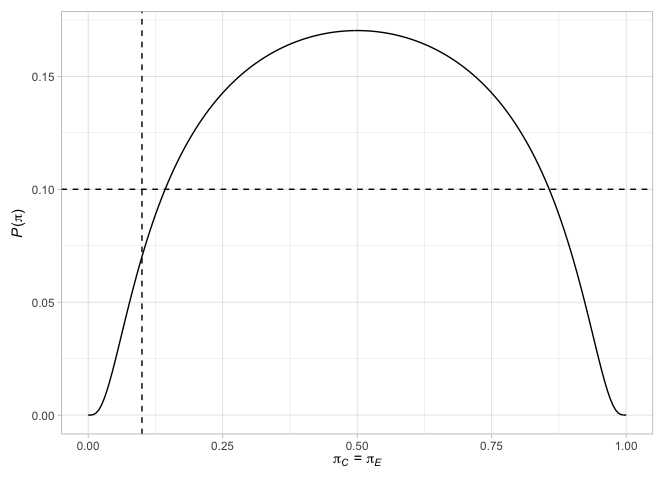
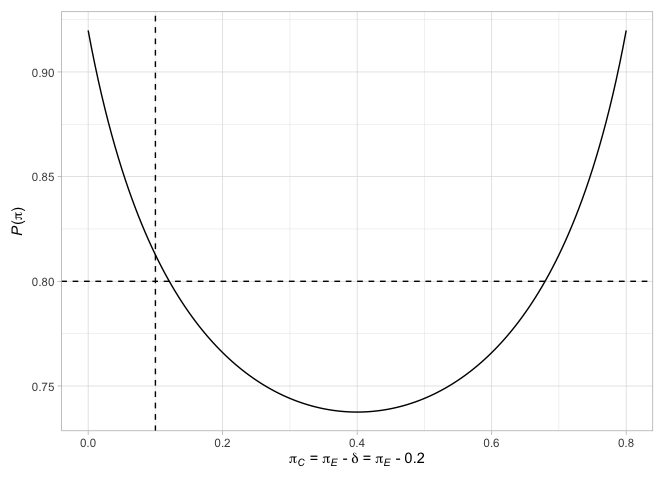
انظر الحزمة المقالات القصيرة لمزيد من التفاصيل.
Jung SH (2008) تجارب المرحلة الثانية العشوائية مع سيطرة محتملة. Stat Med 27 (4): 568–83. doi: 10.1002/sim.2961. بميد: 17573688.
Jung SH ، Sargent DJ (2014) التجارب السريرية المرحلة الثانية العشوائية. J Biopharm Stat 24 (4): 802–16. doi: 10.1080/10543406.2014.901343. بميد: 24697589.
Kepner JL (2010) على التصميمات المتسلسلة للمجموعة تقارن نسبتين ذوو الحدين. J Biopharm Stat 20 (1): 145–59. doi: 10.1080/10543400903280621. بميد: 20077254.
Litwin S ، Basickes S ، Ross EA (2017) تجارب ثنائية العينة ثنائية المرحلة 2 مع خطأ منخفض من النوع الأول وحجم العينة المنخفض. Stat Med 36 (9): 1383–94. doi: 10.1002/sim.7226. بميد: 28118686.
Shan G ، Ma C ، Hutson AD ، Wilding GE (2013) تصميمات عشوائية المرحلة الثانية من المرحلة الثانية من المرحلة الثانية على أساس اختبار بارنارد الدقيق. J Biopharm Stat 23 (5): 1081–90. doi: 10.1080/10543406.2013.813525. بميد: 23957517.