Sort_Algorithms
V1.1
一個程序,顯示執行時間和用C語言對算法進行排序的變化。有48種分類算法可用分佈在8種不同的類別中。
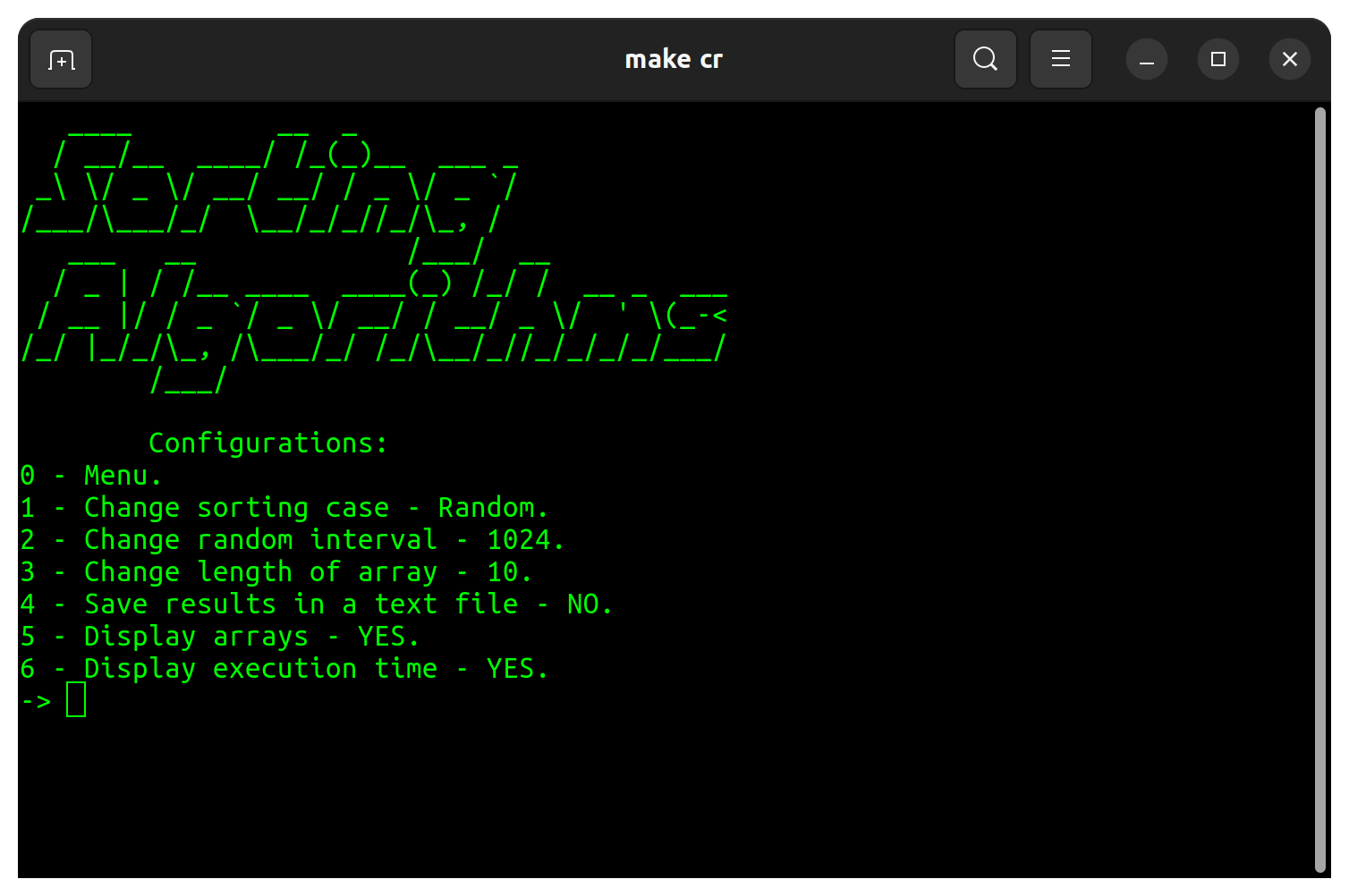
在程序設置上,下表中指出了可用的修改:
| 配置 | 預設 |
|---|---|
| 排序案例 | 隨機的 |
| 隨機間隔 | 32 |
| 陣列的長度 | 10 |
| 將結果保存在文本文件中 | 不 |
| 顯示數組 | 是的 |
| 顯示執行時間 | 是的 |
注意:您需要在計算機中安裝GCC編譯器才能執行以下說明以運行程序。
打開終端並轉到項目目錄。在終端中make允許編譯程序。命令可以使用Make( make ${command} )執行:
| 命令 | 描述 |
|---|---|
| 乾淨的 | 清除生成的所有對象 |
| Cr | 編譯和運行 |
| rmproper | 清除所有對象文件 |
| 跑步 | 執行主程序 |
在命令提示或powerShell上,然後轉到項目目錄並execute.bat 。
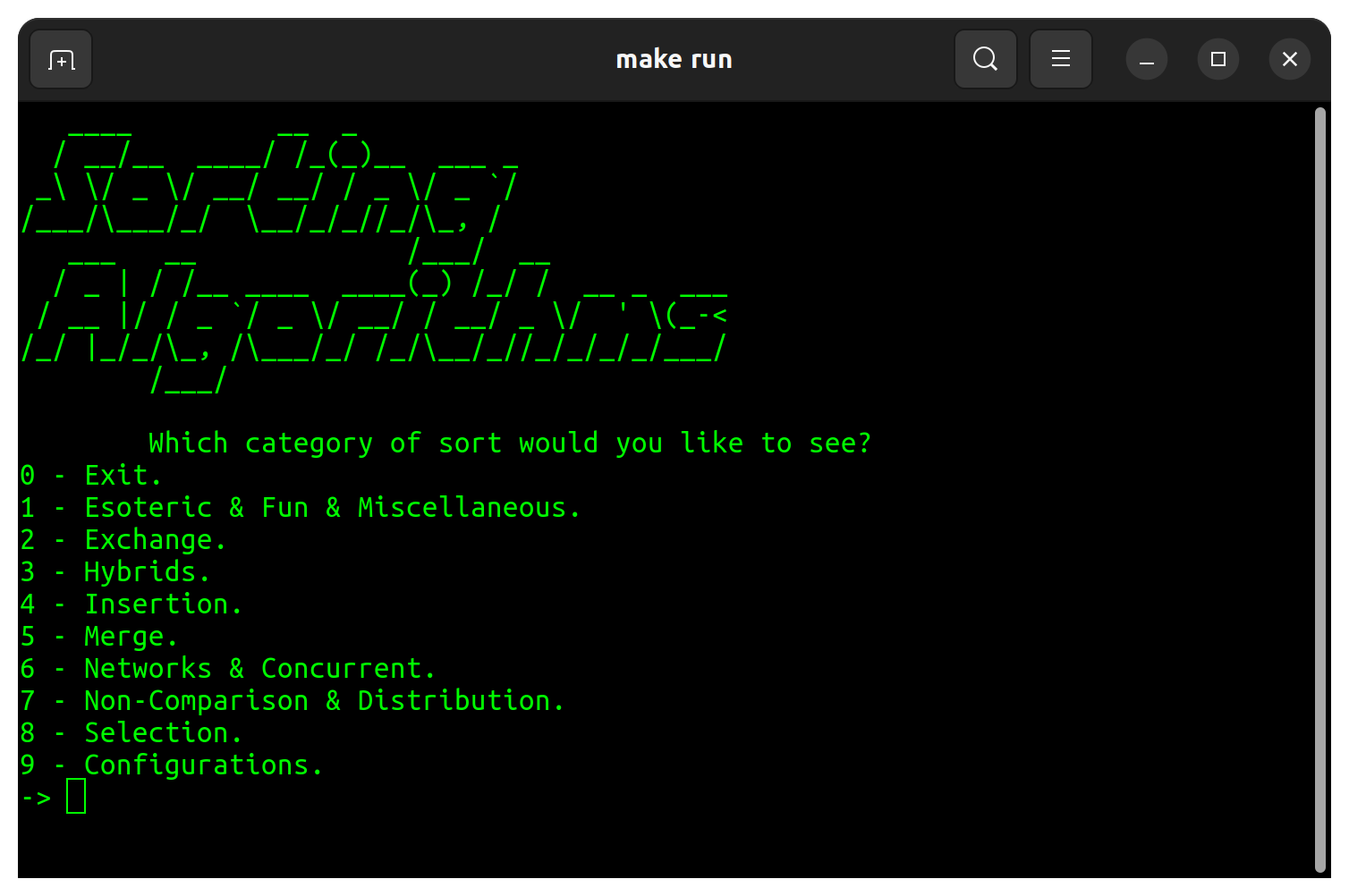
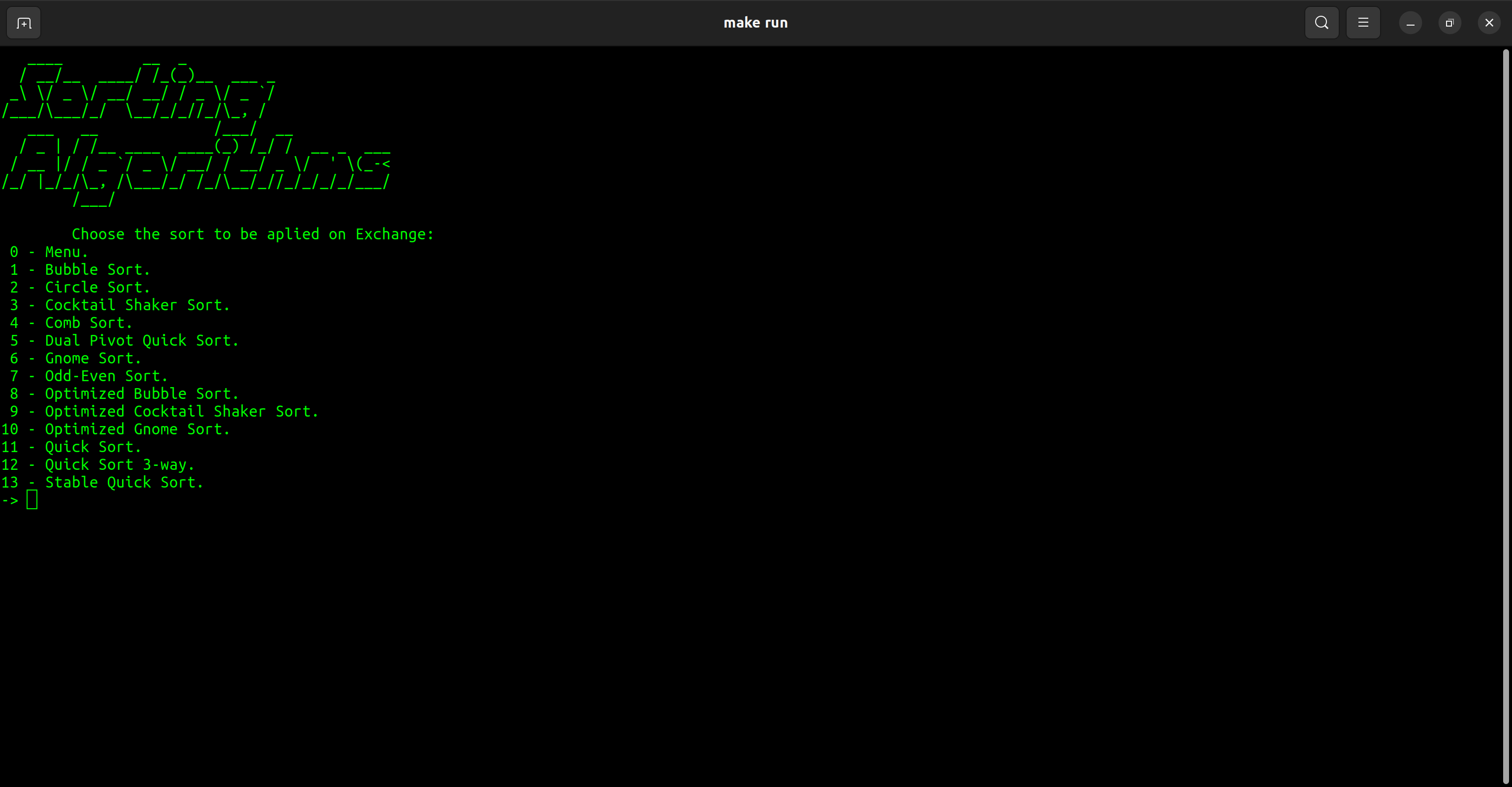
| 類別 | 種類 |
|---|---|
| 深奧,娛樂和雜項 | 不好 Bogo Bogo排序 Bogo排序 泡泡bogo排序 雞尾酒Bogo排序 Exchange Bogo排序 較少的bogo排序 煎餅排序 愚蠢的排序 睡眠排序 慢排序 意大利麵條 Stooge排序 |
| 交換 | 氣泡排序 圓排序 雞尾酒振盪器排序 梳子排序 雙樞軸快速排序 侏儒排序 奇怪的是 優化的氣泡排序 優化的雞尾酒振盪器排序 優化的侏儒排序 快速排序 快速排序3向 穩定的快速排序 |
| 雜種 | 蒂姆排序 |
| 插入 | AVL樹排序 二進制插入排序 週期排序 插入排序 耐心排序 外殼排序 樹排序 |
| 合併 | 自下而上的合併排序 現場合併排序 合併排序 |
| 網絡和並發 | Bitonic排序 成對網絡排序 |
| 不適合和分銷 | 水桶排序 計數排序 重力(珠)排序 鴿洞排序 Radix LSD排序 |
| 選擇 | 雙重選擇排序 最大堆排序 最小堆排序 選擇排序 |
| 演算法 | 最壞的情況 | 最好的情況 | 平均的 | 空間複雜性 | 就地 | 穩定的 | 筆記 |
|---|---|---|---|---|---|---|---|
| 不好 | o(n³) | o(n³) | o(n³) | o(1) | ✔️ | ||
| Bogo Bogo排序 | o(無窮大) | o(n²) | o((n+1)!) | o(1) | ✔️ | 由於隨機操縱,最壞的情況可能是無限的 | |
| Bogo排序 | o(無窮大) | 在) | o((n+1)!) | o(1) | ✔️ | 由於隨機操縱,最壞的情況可能是無限的 | |
| 泡泡bogo排序 | o(無窮大) | 在) | o((n+1)!) | o(1) | ✔️ | ✔️ | 由於隨機操縱,最壞的情況可能是無限的 |
| 雞尾酒Bogo排序 | o(無窮大) | 在) | o((n+1)!) | o(1) | ✔️ | 由於隨機操縱,最壞的情況可能是無限的 | |
| Exchange Bogo排序 | o(無窮大) | 在) | o((n+1)!) | o(1) | ✔️ | 由於隨機操縱,最壞的情況可能是無限的 | |
| 較少的bogo排序 | o(無窮大) | o(n²) | o((n+1)!) | o(1) | ✔️ | 由於隨機操縱,最壞的情況可能是無限的 | |
| 煎餅排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ||
| 愚蠢的排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ||
| 睡眠排序 | o(int_max) | O(最大(輸入) + n) | O(最大(輸入) + n) | 在) | ✔️ | 使用CPU調度程序排序 | |
| 慢排序 | o(n*n!) | 在) | o((n+1)!) | o(1) | ✔️ | ||
| 意大利麵條 | 在) | 在) | 在) | 在) | ✔️ | ||
| Stooge排序 |  |  |  | 在) | |||
| 氣泡排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 圓排序 | o(n log n log n) | o(n log n) | o(n log n) | o(1) | ✔️ | ||
| 雞尾酒振盪器排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ✔️ | |
| 梳子排序 | o(n²) | o(n log n) | 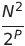 | o(1) | ✔️ | P是增量的數量 | |
| 雙樞軸快速排序 | o(n²) | o(n log n) | o(n log n) | o(log n) | ✔️ | ||
| 侏儒排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 奇怪的是 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 優化的氣泡排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 優化的雞尾酒振盪器排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 優化的侏儒排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 快速排序 | o(n²) | o(n log n) | o(n log n) | o(log n) | ✔️ | ||
| 快速排序3向 | o(n²) | 在) | o(n log n) | o(log n)或o(n) | ✔️ | ||
| 穩定的快速排序 | o(n²) | o(n log n) | o(n log n) | 在) | ✔️ | ✔️ | |
| 蒂姆排序 | o(n log n) | 在) | o(n log n) | 在) | ✔️ | ||
| AVL樹排序 | o(n log n) | 在) | o(n log n) | 在) | ✔️ | 在最壞的情況下,使用二進制搜索樹和O(n log n)使用自平衡二進制搜索樹時 | |
| 二進制插入排序 | o(n log n) | 在) | o(n log n) | o(1) | ✔️ | ✔️ | |
| 週期排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ||
| 插入排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 耐心排序 | o(n log n) | 在) | o(n log n) | 在) | ✔️ | ||
| 外殼排序 | 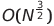 或o(nlog²n) 或o(nlog²n) | o(n log n) | o(n^1.25)至o(n²) | o(1) | ✔️ | ||
| 樹排序 | o(n²) | o(n log n) | o(n log n) | 在) | ✔️ | 在最壞的情況下,使用二進制搜索樹和O(n log n)使用自平衡二進制搜索樹時 | |
| 自下而上的合併排序 | o(n log n) | o(n log n) | o(n log n) | 在) | ✔️ | ||
| 現場合併排序 | o(n²) | o(n²) | o(n²) | o(log n) | ✔️ | ✔️ | |
| 合併排序 | o(n log n) | o(n log n) | o(n log n) | 在) | ✔️ | ||
| Bitonic排序 | o(log²n) | o(log²n) | o(log²n) | o(nlog²n) | ✔️ | ||
| 成對網絡排序 | 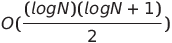 或o(n log n) 或o(n log n) | o(n log n) | o(n log n) | 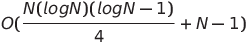 | ✔️ | 最壞的情況是使用並行時間和空間複雜性非平行時間 | |
| 水桶排序 | o(n²) | o(n+k) | o(n+k) | o(n+k) | ✔️ | k是水桶的數量 | |
| 計數排序 | o(n+k) | o(n+k) | o(n+k) | o(n+k) | ✔️ | k是輸入數據的範圍 | |
| 重力(珠)排序 | o(s) | o(1)或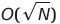 | 在) | o(n²) | ✔️ | s是數組元素的總和,o(1)不能在實踐中實現 | |
| 鴿洞排序 | o(n+n) | o(n+n) | o(n+n) | o(n+n) | ✔️ | n是元素的數量, n是輸入數據的範圍 | |
| Radix LSD排序 | O(NW) | O(NW) | O(NW) | 在) | ✔️ | W是最大元素寬度(位) | |
| 雙重選擇排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | 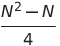 比較 比較 | |
| 最大堆排序 | o(n log n) | o(n log n) | o(n log n) | o(1) | ✔️ | ||
| 最小堆排序 | o(n log n) | o(n log n) | o(n log n) | o(1) | ✔️ | ||
| 選擇排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | 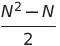 比較 比較 |