Sort_Algorithms
V1.1
Ein Programm, mit dem die Ausführungszeit und die Varize der Sortierung von Algorithmen in C -Sprache angezeigt werden. Es gibt 48 Sortieralgorithmen, die in 8 verschiedenen Kategorien verteilt sind.
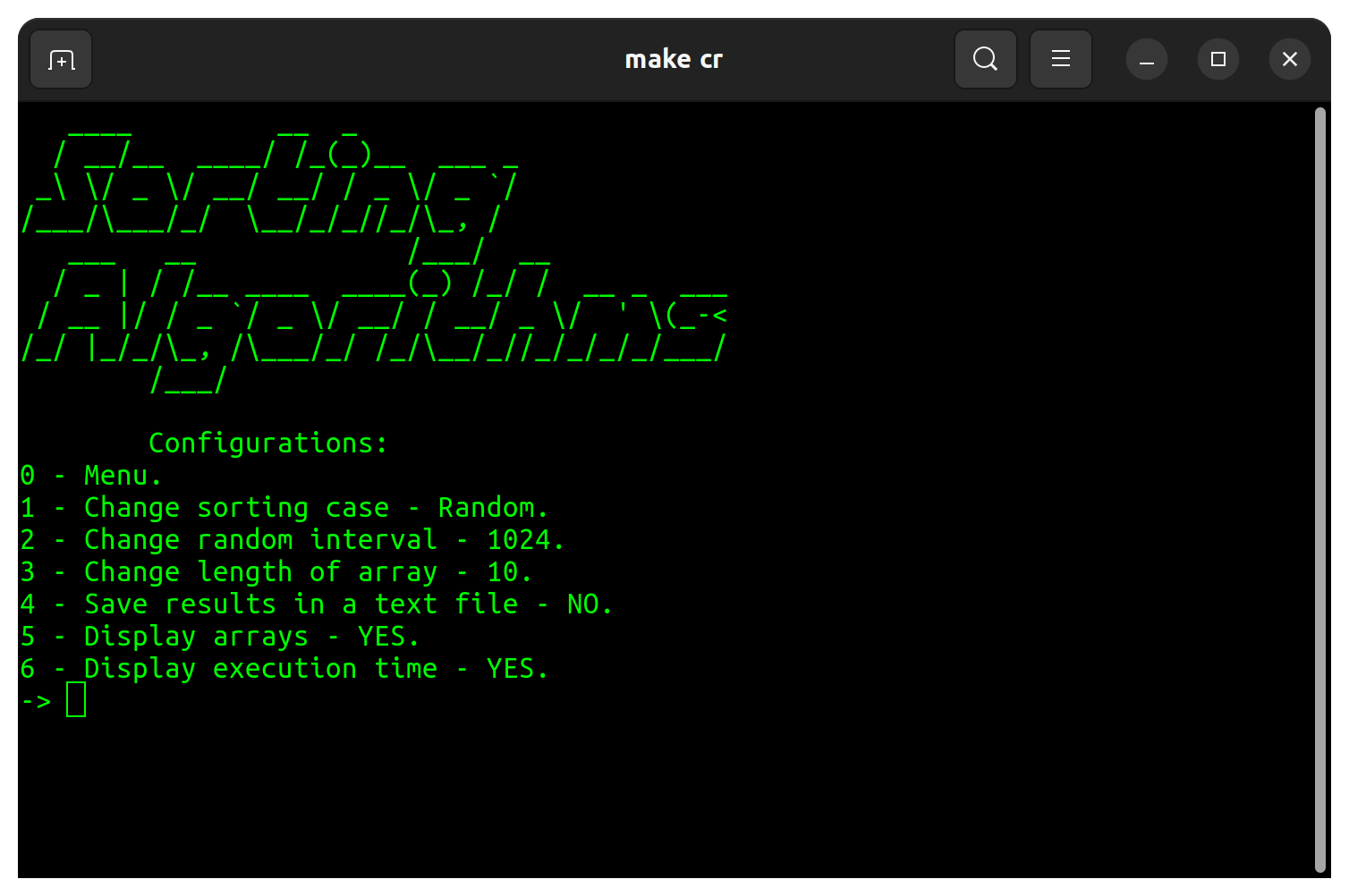
Bei den Programmeinstellungen sind in der Tabelle unten durchschnittliche Änderungen festgestellt:
| Konfiguration | Standard |
|---|---|
| Sortierfall | Zufällig |
| Zufällige Intervall | 32 |
| Länge des Arrays | 10 |
| Speichern Sie Ergebnisse in einer Textdatei | NEIN |
| Arrays anzeigen | JA |
| Ausführungszeit anzeigen | JA |
Hinweis: Sie müssen den GCC -Compiler in Ihrem Computer installieren lassen, um die folgenden Anweisungen auszuführen, um das Programm auszuführen.
Öffnen Sie ein Terminal und gehen Sie zum Projekt des Projekts. make in terminal erlauben das Programm zu kompilieren. Befehle, die mit Make ( make ${command} ) auszuführen sind:
| Befehl | Beschreibung |
|---|---|
| sauber | Alle erzeugten Objekte löschen |
| Cr | Kompilieren und rennen |
| rmproper | Alle Objektdateien löschen |
| laufen | Hauptprogramm ausführen |
Auf Eingabeaufforderung oder PowerShell und in das Verzeichnis des Projekts gehen und execute.bat ausführen.
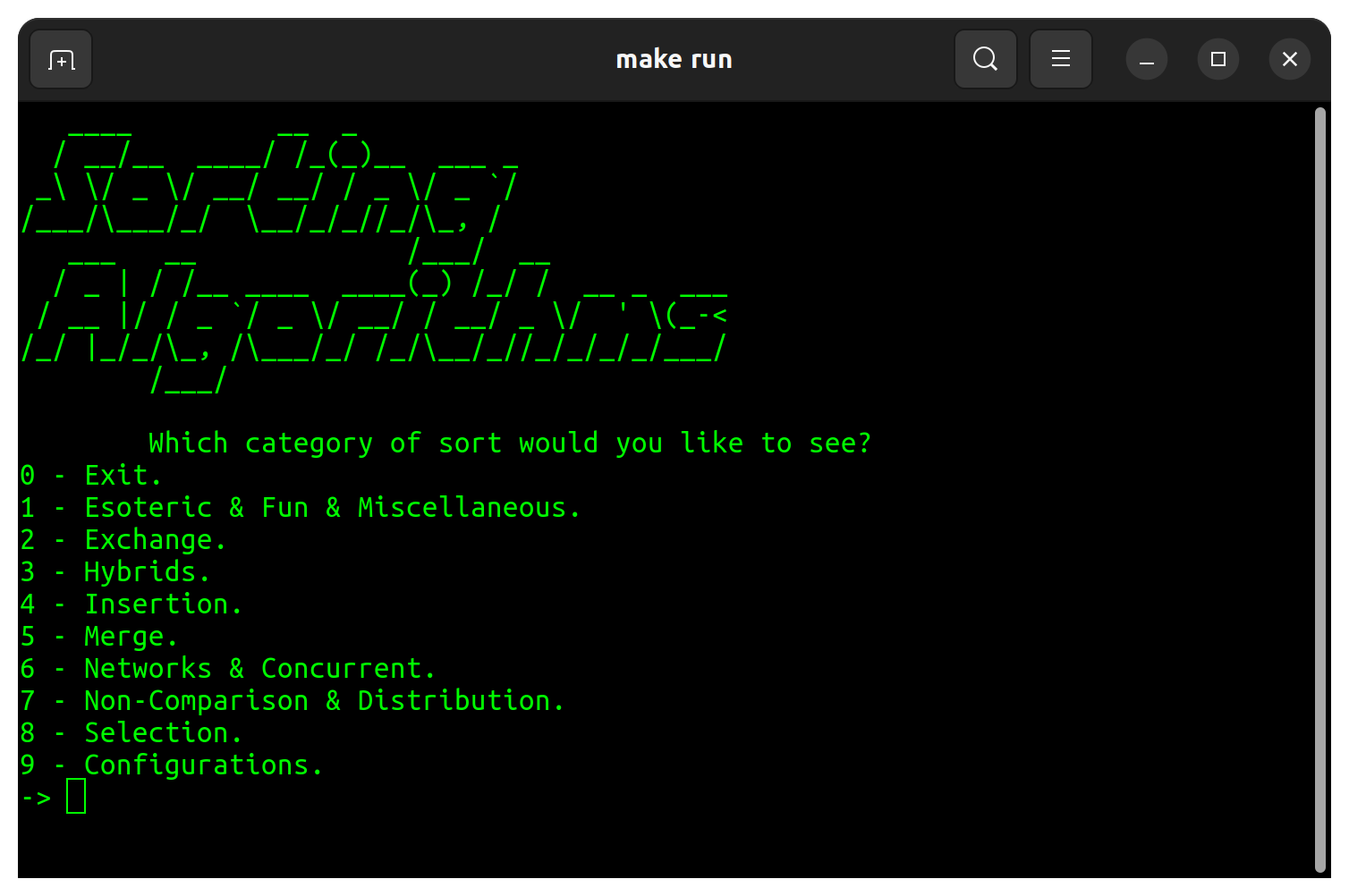
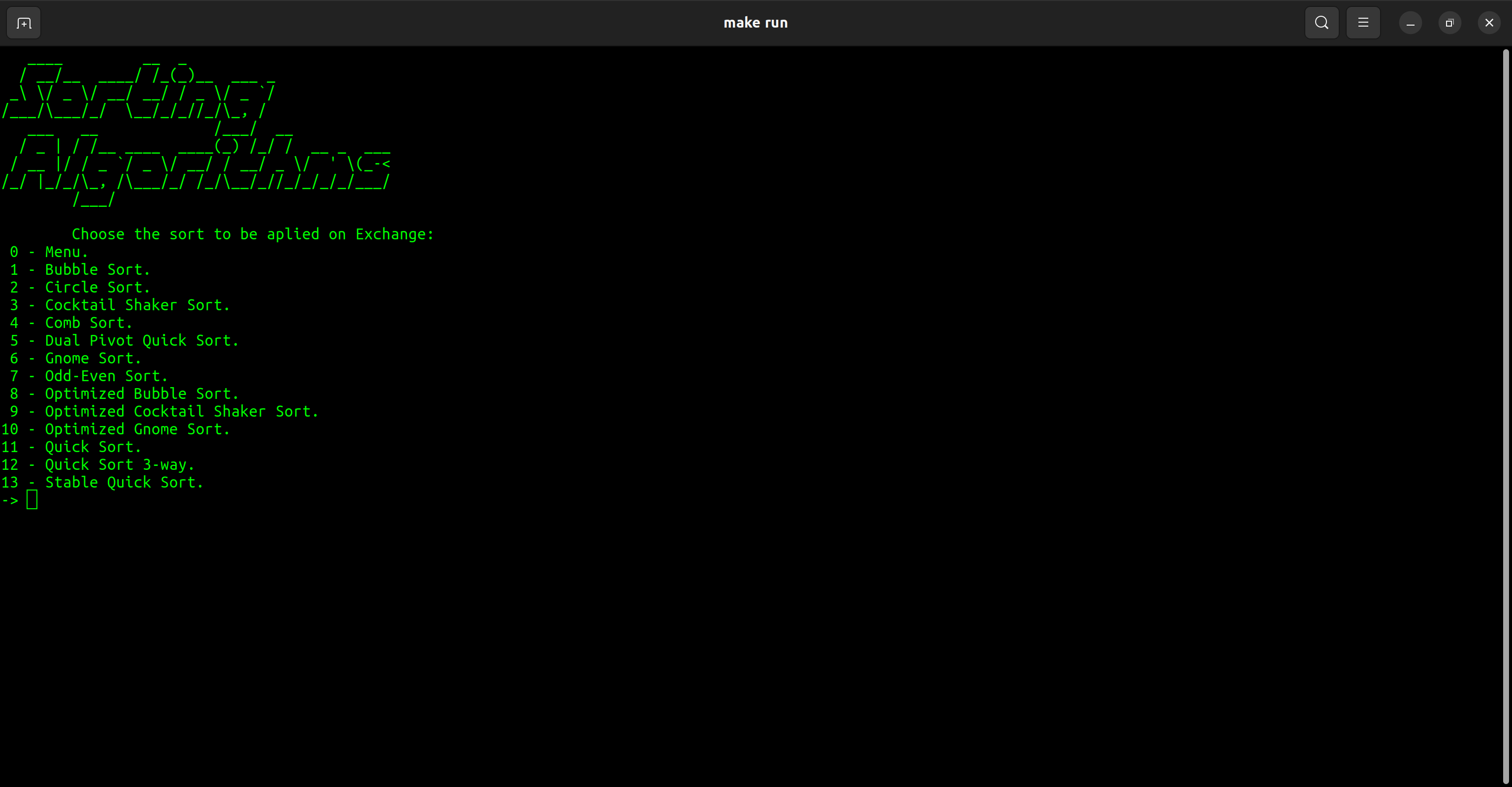
| Kategorie | Sortieren |
|---|---|
| Esoterisch & lustig & verschieden | Schlechte Art Bogo Bogo Sort Bogo Sort Bubble Bogo Sort Cocktail Bogo Sort Bogo -Sortierung austauschen Weniger Bogo -Sort Pfannkuchen -Sort Alberne Sorte Schlafsart Langsame Art Spaghetti -Art Sortierstöckchen |
| Austausch | Blasenart Kreis Sortierung Cocktail Shaker Sort Kammsart Dual Pivot Quick Sort Gnom -Sort Seltsame Art Optimierte Blasensortierung Optimierte Cocktail Shaker -Sortierung Optimierte Gnom -Sorte Schnelle Sortierung Schnelle Sortierung 3-Wege Stabile schnelle Sorte |
| Hybriden | Tim Art |
| Einfügen | AVL -Baumsortierung Binärinsertionsart Zyklusart Insertion -Sortierung Geduld Sortierung Shell -Sortierung Baumart |
| Verschmelzen | Bottom-up-Zusammenführungsart In-Place-Zusammenführungsart Sortierung zusammenführen |
| Netzwerke und gleichzeitiger | Bitonische Sorte Paarweise Netzwerksortierung |
| Nichtvergleich und Verbreitung | Eimer -Sort Zählsart Schwerkraft (Perle) Sortierung Taubenloch -Art Radix LSD -Sortierung |
| Auswahl | Doppelauswahl -Sortierung Max Haufensart Min Haufensart Auswahlsart |
| Algorithmus | Schlimmster Fall | Bester Fall | Durchschnitt | Raumkomplexität | Einort | Stabil | Notizen |
|---|---|---|---|---|---|---|---|
| Schlechte Art | O (n³) | O (n³) | O (n³) | O (1) | ✔️ | ||
| Bogo Bogo Sort | O (Unendlichkeit) | O (n²) | O ((n+1)!) | O (1) | ✔️ | Der schlimmste Fall kann aufgrund zufälliger Manipulation unbegrenzt werden | |
| Bogo Sort | O (Unendlichkeit) | AN) | O ((n+1)!) | O (1) | ✔️ | Der schlimmste Fall kann aufgrund zufälliger Manipulation unbegrenzt werden | |
| Bubble Bogo Sort | O (Unendlichkeit) | AN) | O ((n+1)!) | O (1) | ✔️ | ✔️ | Der schlimmste Fall kann aufgrund zufälliger Manipulation unbegrenzt werden |
| Cocktail Bogo Sort | O (Unendlichkeit) | AN) | O ((n+1)!) | O (1) | ✔️ | Der schlimmste Fall kann aufgrund zufälliger Manipulation unbegrenzt werden | |
| Bogo -Sortierung austauschen | O (Unendlichkeit) | AN) | O ((n+1)!) | O (1) | ✔️ | Der schlimmste Fall kann aufgrund zufälliger Manipulation unbegrenzt werden | |
| Weniger Bogo -Sort | O (Unendlichkeit) | O (n²) | O ((n+1)!) | O (1) | ✔️ | Der schlimmste Fall kann aufgrund zufälliger Manipulation unbegrenzt werden | |
| Pfannkuchen -Sort | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Alberne Sorte | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Schlafsart | O (int_max) | O (max (Eingabe) + n) | O (max (Eingabe) + n) | AN) | ✔️ | Nutzen Sie die CPU -Scheduler, um sie zu sortieren | |
| Langsame Art | O (n*n!) | AN) | O ((n+1)!) | O (1) | ✔️ | ||
| Spaghetti -Art | AN) | AN) | AN) | AN) | ✔️ | ||
| Sortierstöckchen |  |  |  | AN) | |||
| Blasenart | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Kreis Sortierung | O (n log n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Cocktail Shaker Sort | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ✔️ | |
| Kammsart | O (n²) | O (n log n) | 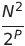 | O (1) | ✔️ | P ist die Anzahl der Schritte | |
| Dual Pivot Quick Sort | O (n²) | O (n log n) | O (n log n) | O (log n) | ✔️ | ||
| Gnom -Sort | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Seltsame Art | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Optimierte Blasensortierung | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Optimierte Cocktail Shaker -Sortierung | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Optimierte Gnom -Sorte | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Schnelle Sortierung | O (n²) | O (n log n) | O (n log n) | O (log n) | ✔️ | ||
| Schnelle Sortierung 3-Wege | O (n²) | AN) | O (n log n) | O (log n) oder o (n) | ✔️ | ||
| Stabile schnelle Sorte | O (n²) | O (n log n) | O (n log n) | AN) | ✔️ | ✔️ | |
| Tim Art | O (n log n) | AN) | O (n log n) | AN) | ✔️ | ||
| AVL -Baumsortierung | O (n log n) | AN) | O (n log n) | AN) | ✔️ | Im schlimmsten Fall, O (n²) bei der Verwendung von Binär-Suchbaum und O (n log n) bei der Verwendung eines selbstausgleicheren Binär-Suchbaums | |
| Binärinsertionsart | O (n log n) | AN) | O (n log n) | O (1) | ✔️ | ✔️ | |
| Zyklusart | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Insertion -Sortierung | O (n²) | AN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Geduld Sortierung | O (n log n) | AN) | O (n log n) | AN) | ✔️ | ||
| Shell -Sortierung | 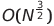 oder o (n log² n) oder o (n log² n) | O (n log n) | O (n^1,25) bis o (n²) | O (1) | ✔️ | ||
| Baumart | O (n²) | O (n log n) | O (n log n) | AN) | ✔️ | Im schlimmsten Fall, O (n²) bei der Verwendung von Binär-Suchbaum und O (n log n) bei der Verwendung eines selbstausgleicheren Binär-Suchbaums | |
| Bottom-up-Zusammenführungsart | O (n log n) | O (n log n) | O (n log n) | AN) | ✔️ | ||
| In-Place-Zusammenführungsart | O (n²) | O (n²) | O (n²) | O (log n) | ✔️ | ✔️ | |
| Sortierung zusammenführen | O (n log n) | O (n log n) | O (n log n) | AN) | ✔️ | ||
| Bitonische Sorte | O (log² n) | O (log² n) | O (log² n) | O (n log² n) | ✔️ | ||
| Paarweise Netzwerksortierung | 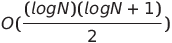 oder o (n log n) oder o (n log n) | O (n log n) | O (n log n) | 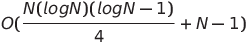 | ✔️ | Der schlimmste Fall ist die Verwendung paralleler Zeit und Raumkomplexität nicht parallel | |
| Eimer -Sort | O (n²) | O (n+k) | O (n+k) | O (n+k) | ✔️ | K ist die Anzahl der Eimer | |
| Zählsart | O (n+k) | O (n+k) | O (n+k) | O (n+k) | ✔️ | K ist der Bereich der Eingabedaten | |
| Schwerkraft (Perle) Sortierung | O (s) | O (1) oder 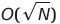 | AN) | O (n²) | ✔️ | S ist die Summe der Array -Elemente, o (1) kann in der Praxis nicht implementiert werden | |
| Taubenloch -Art | O (n+n) | O (n+n) | O (n+n) | O (n+n) | ✔️ | N ist die Anzahl der Elemente und n ist der Bereich der Eingabedaten | |
| Radix LSD -Sortierung | O (NW) | O (NW) | O (NW) | AN) | ✔️ | W ist die Maxumum -Elementbreite (Bits) | |
| Doppelauswahl -Sortierung | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | 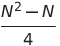 Vergleiche Vergleiche | |
| Max Haufensart | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Min Haufensart | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Auswahlsart | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | 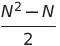 Vergleiche Vergleiche |