Sort_Algorithms
V1.1
A program to show the execution time and the variaty of sorting algorithms in C language. There are 48 sorting algorithms avaliable distributed in 8 different categories.
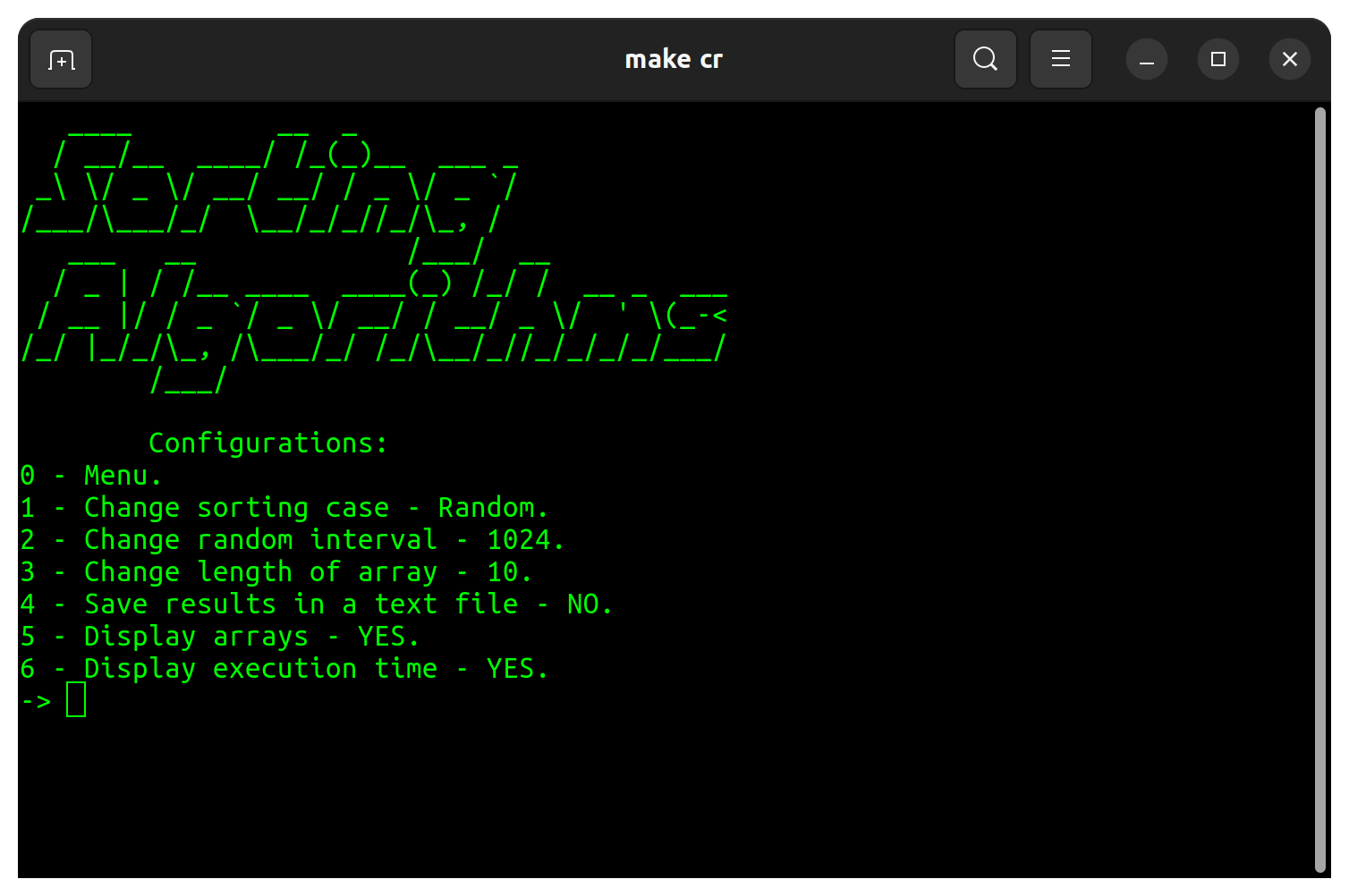
On program settings there are avaliable modifications noted in table below:
| Configuration | Default |
|---|---|
| Sorting case | Random |
| Random interval | 32 |
| Length of array | 10 |
| Save results in a text file | NO |
| Display arrays | YES |
| Display execution time | YES |
Note: you need to have the GCC compiler installed in your machine to execute the instructions below to run the program.
Open a terminal and go to project's directory. Execute make in terminal allow to compile the program. Commands avaliable to execute with make (make ${command}):
| Command | Description |
|---|---|
| clean | Clear all objects generated |
| cr | Compile and run |
| rmproper | Clear all object files |
| run | Execute main program |
On Command Prompt or PowerShell and go to project's directory and execute execute.bat.
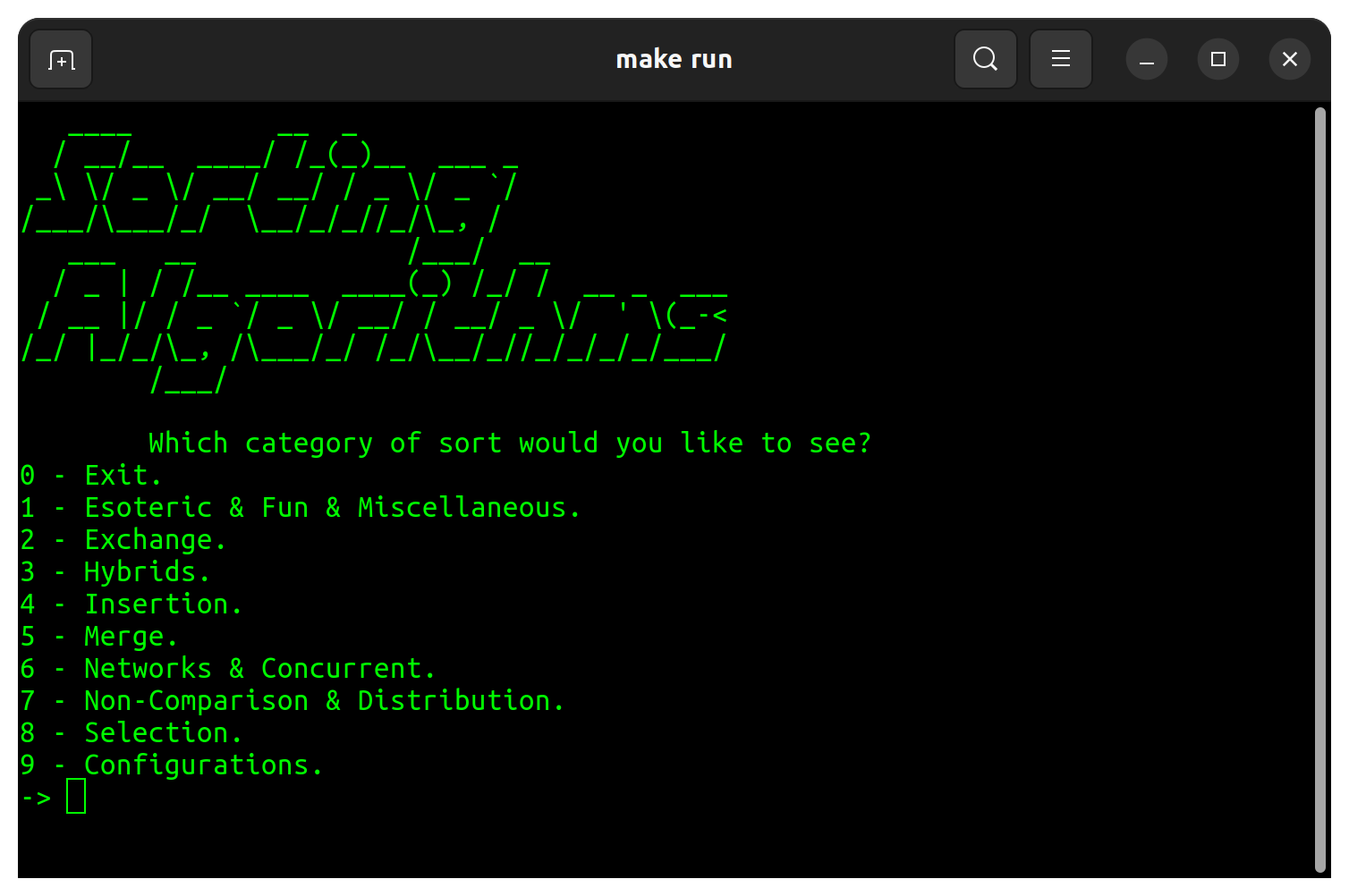
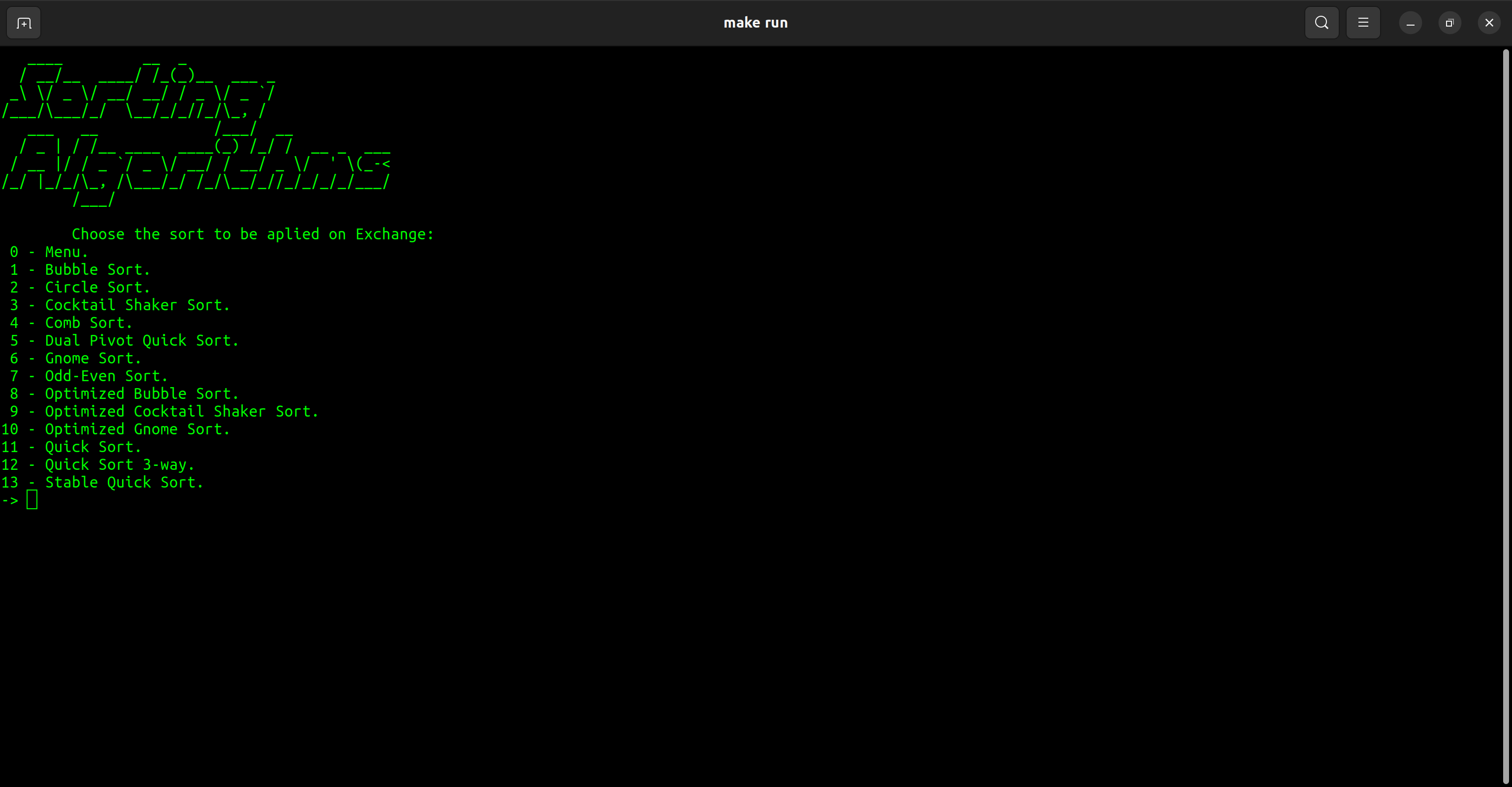
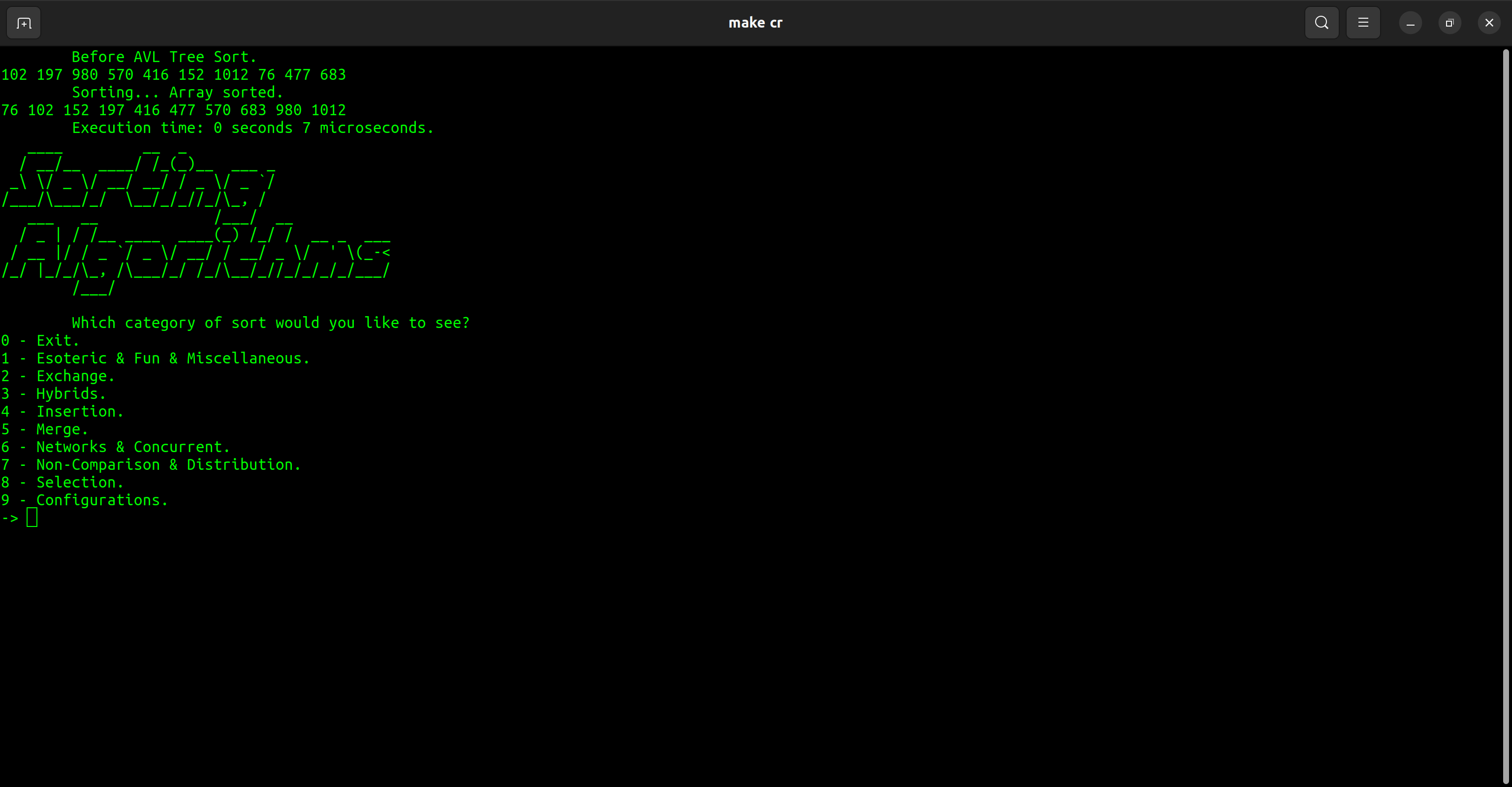
| Category | Sort |
|---|---|
| Esoteric & Fun & Miscellaneous | Bad Sort Bogo Bogo Sort Bogo Sort Bubble Bogo Sort Cocktail Bogo Sort Exchange Bogo Sort Less Bogo Sort Pancake Sort Silly Sort Sleep Sort Slow Sort Spaghetti Sort Stooge Sort |
| Exchange | Bubble Sort Circle Sort Cocktail Shaker Sort Comb Sort Dual Pivot Quick Sort Gnome Sort Odd-Even Sort Optimized Bubble Sort Optimized Cocktail Shaker Sort Optimized Gnome Sort Quick Sort Quick Sort 3-way Stable Quick Sort |
| Hybrids | Tim Sort |
| Insertion | AVL Tree Sort Binary Insertion Sort Cycle Sort Insertion Sort Patience Sort Shell Sort Tree Sort |
| Merge | Bottom-up Merge Sort In-Place Merge Sort Merge Sort |
| Networks & Concurrent | Bitonic Sort Pairwise Network Sort |
| Non-Comparison & Distribution | Bucket Sort Counting Sort Gravity (Bead) Sort Pigeonhole Sort Radix LSD Sort |
| Selection | Double Selection Sort Max Heap Sort Min Heap Sort Selection Sort |
| Algorithm | Worst case | Best case | Average | Space complexity | In-place | Stable | Notes |
|---|---|---|---|---|---|---|---|
| Bad Sort | O(N³) | O(N³) | O(N³) | O(1) | ✔️ | ||
| Bogo Bogo Sort | O(infinity) | O(N²) | O((N+1)!) | O(1) | ✔️ | The worst case can be unbounded due to random manipulation | |
| Bogo Sort | O(infinity) | O(N) | O((N+1)!) | O(1) | ✔️ | The worst case can be unbounded due to random manipulation | |
| Bubble Bogo Sort | O(infinity) | O(N) | O((N+1)!) | O(1) | ✔️ | ✔️ | The worst case can be unbounded due to random manipulation |
| Cocktail Bogo Sort | O(infinity) | O(N) | O((N+1)!) | O(1) | ✔️ | The worst case can be unbounded due to random manipulation | |
| Exchange Bogo Sort | O(infinity) | O(N) | O((N+1)!) | O(1) | ✔️ | The worst case can be unbounded due to random manipulation | |
| Less Bogo Sort | O(infinity) | O(N²) | O((N+1)!) | O(1) | ✔️ | The worst case can be unbounded due to random manipulation | |
| Pancake Sort | O(N²) | O(N²) | O(N²) | O(1) | ✔️ | ||
| Silly Sort | O(N²) | O(N²) | O(N²) | O(1) | ✔️ | ||
| Sleep Sort | O(INT_MAX) | O(max(input) + N) | O(max(input) + N) | O(N) | ✔️ | Take use of CPU scheduler to sort | |
| Slow Sort | O(N*N!) | O(N) | O((N+1)!) | O(1) | ✔️ | ||
| Spaghetti Sort | O(N) | O(N) | O(N) | O(N) | ✔️ | ||
| Stooge Sort |  |
 |
 |
O(N) | |||
| Bubble Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Circle Sort | O(N log N log N) | O(N log N) | O(N log N) | O(1) | ✔️ | ||
| Cocktail Shaker Sort | O(N²) | O(N²) | O(N²) | O(1) | ✔️ | ✔️ | |
| Comb Sort | O(N²) | O(N log N) | 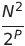 |
O(1) | ✔️ | P is the number of increments | |
| Dual Pivot Quick Sort | O(N²) | O(N log N) | O(N log N) | O(log N) | ✔️ | ||
| Gnome Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Odd-Even Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Optimized Bubble Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Optimized Cocktail Shaker Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Optimized Gnome Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Quick Sort | O(N²) | O(N log N) | O(N log N) | O(log N) | ✔️ | ||
| Quick Sort 3-way | O(N²) | O(N) | O(N log N) | O(log N) or O(N) | ✔️ | ||
| Stable Quick Sort | O(N²) | O(N log N) | O(N log N) | O(N) | ✔️ | ✔️ | |
| Tim Sort | O(N log N) | O(N) | O(N log N) | O(N) | ✔️ | ||
| AVL Tree Sort | O(N log N) | O(N) | O(N log N) | O(N) | ✔️ | In worst case, O(N²) when using Binary Search Tree and O(N log N) when using Self-Balanced Binary Search Tree | |
| Binary Insertion Sort | O(N log N) | O(N) | O(N log N) | O(1) | ✔️ | ✔️ | |
| Cycle Sort | O(N²) | O(N²) | O(N²) | O(1) | ✔️ | ||
| Insertion Sort | O(N²) | O(N) | O(N²) | O(1) | ✔️ | ✔️ | |
| Patience Sort | O(N log N) | O(N) | O(N log N) | O(N) | ✔️ | ||
| Shell Sort | 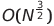 or O(N log² N) or O(N log² N) |
O(N log N) | O(N^1.25) to O(N²) | O(1) | ✔️ | ||
| Tree Sort | O(N²) | O(N log N) | O(N log N) | O(N) | ✔️ | In worst case, O(N²) when using Binary Search Tree and O(N log N) when using Self-Balanced Binary Search Tree | |
| Bottom-up Merge Sort | O(N log N) | O(N log N) | O(N log N) | O(N) | ✔️ | ||
| In-Place Merge Sort | O(N²) | O(N²) | O(N²) | O(log N) | ✔️ | ✔️ | |
| Merge Sort | O(N log N) | O(N log N) | O(N log N) | O(N) | ✔️ | ||
| Bitonic Sort | O(log² N) | O(log² N) | O(log² N) | O(N log² N) | ✔️ | ||
| Pairwise Network Sort | 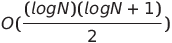 or O(N log N) or O(N log N) |
O(N log N) | O(N log N) | 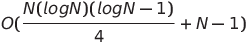 |
✔️ | Worst case is using parallel time and space complexity non-parallel time | |
| Bucket Sort | O(N²) | O(N+k) | O(N+k) | O(N+k) | ✔️ | k is the number of buckets | |
| Counting Sort | O(N+k) | O(N+k) | O(N+k) | O(N+k) | ✔️ | k is the range of input data | |
| Gravity (Bead) Sort | O(S) | O(1) or 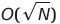 |
O(N) | O(N²) | ✔️ | S is the sum of array elements, O(1) cannot be implemented in practice | |
| Pigeonhole Sort | O(N+n) | O(N+n) | O(N+n) | O(N+n) | ✔️ | N is the number of elements and n is the range of input data | |
| Radix LSD Sort | O(NW) | O(NW) | O(NW) | O(N) | ✔️ | W is the maxumum element width (bits) | |
| Double Selection Sort | O(N²) | O(N²) | O(N²) | O(1) | ✔️ | 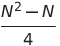 Comparisons Comparisons |
|
| Max Heap Sort | O(N log N) | O(N log N) | O(N log N) | O(1) | ✔️ | ||
| Min Heap Sort | O(N log N) | O(N log N) | O(N log N) | O(1) | ✔️ | ||
| Selection Sort | O(N²) | O(N²) | O(N²) | O(1) | ✔️ | 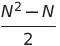 Comparisons Comparisons |