Sort_Algorithms
V1.1
一个程序,显示执行时间和用C语言对算法进行排序的变化。有48种分类算法可用分布在8种不同的类别中。
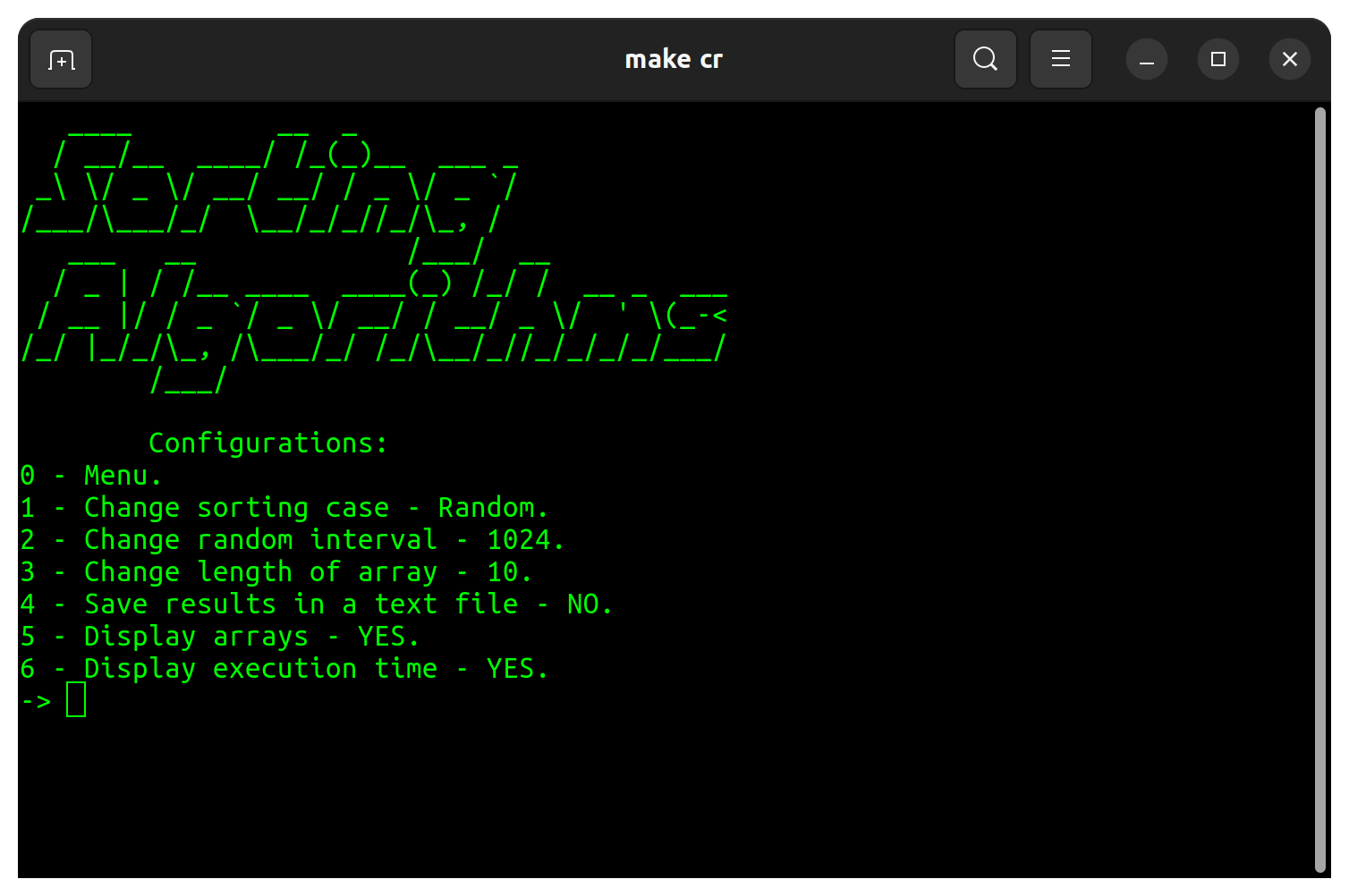
在程序设置上,下表中指出了可用的修改:
| 配置 | 默认 |
|---|---|
| 排序案例 | 随机的 |
| 随机间隔 | 32 |
| 阵列的长度 | 10 |
| 将结果保存在文本文件中 | 不 |
| 显示数组 | 是的 |
| 显示执行时间 | 是的 |
注意:您需要在计算机中安装GCC编译器才能执行以下说明以运行程序。
打开终端并转到项目目录。在终端中make允许编译程序。命令可以使用Make( make ${command} )执行:
| 命令 | 描述 |
|---|---|
| 干净的 | 清除生成的所有对象 |
| Cr | 编译和运行 |
| rmproper | 清除所有对象文件 |
| 跑步 | 执行主程序 |
在命令提示或powerShell上,然后转到项目目录并execute.bat 。
| 类别 | 种类 |
|---|---|
| 深奥,娱乐和杂项 | 不好 Bogo Bogo排序 Bogo排序 泡泡bogo排序 鸡尾酒Bogo排序 Exchange Bogo排序 较少的bogo排序 煎饼排序 愚蠢的排序 睡眠排序 慢排序 意大利面条 Stooge排序 |
| 交换 | 气泡排序 圆排序 鸡尾酒振荡器排序 梳子排序 双枢轴快速排序 侏儒排序 奇怪的是 优化的气泡排序 优化的鸡尾酒振荡器排序 优化的侏儒排序 快速排序 快速排序3向 稳定的快速排序 |
| 杂种 | 蒂姆排序 |
| 插入 | AVL树排序 二进制插入排序 周期排序 插入排序 耐心排序 外壳排序 树排序 |
| 合并 | 自下而上的合并排序 现场合并排序 合并排序 |
| 网络和并发 | Bitonic排序 成对网络排序 |
| 不适合和分销 | 水桶排序 计数排序 重力(珠)排序 鸽洞排序 Radix LSD排序 |
| 选择 | 双重选择排序 最大堆排序 最小堆排序 选择排序 |
| 算法 | 最坏的情况 | 最好的情况 | 平均的 | 空间复杂性 | 就地 | 稳定的 | 笔记 |
|---|---|---|---|---|---|---|---|
| 不好 | o(n³) | o(n³) | o(n³) | o(1) | ✔️ | ||
| Bogo Bogo排序 | o(无穷大) | o(n²) | o((n+1)!) | o(1) | ✔️ | 由于随机操纵,最坏的情况可能是无限的 | |
| Bogo排序 | o(无穷大) | 在) | o((n+1)!) | o(1) | ✔️ | 由于随机操纵,最坏的情况可能是无限的 | |
| 泡泡bogo排序 | o(无穷大) | 在) | o((n+1)!) | o(1) | ✔️ | ✔️ | 由于随机操纵,最坏的情况可能是无限的 |
| 鸡尾酒Bogo排序 | o(无穷大) | 在) | o((n+1)!) | o(1) | ✔️ | 由于随机操纵,最坏的情况可能是无限的 | |
| Exchange Bogo排序 | o(无穷大) | 在) | o((n+1)!) | o(1) | ✔️ | 由于随机操纵,最坏的情况可能是无限的 | |
| 较少的bogo排序 | o(无穷大) | o(n²) | o((n+1)!) | o(1) | ✔️ | 由于随机操纵,最坏的情况可能是无限的 | |
| 煎饼排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ||
| 愚蠢的排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ||
| 睡眠排序 | o(int_max) | O(最大(输入) + n) | O(最大(输入) + n) | 在) | ✔️ | 使用CPU调度程序排序 | |
| 慢排序 | o(n*n!) | 在) | o((n+1)!) | o(1) | ✔️ | ||
| 意大利面条 | 在) | 在) | 在) | 在) | ✔️ | ||
| Stooge排序 |  |  |  | 在) | |||
| 气泡排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 圆排序 | o(n log n log n) | o(n log n) | o(n log n) | o(1) | ✔️ | ||
| 鸡尾酒振荡器排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ✔️ | |
| 梳子排序 | o(n²) | o(n log n) | 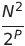 | o(1) | ✔️ | P是增量的数量 | |
| 双枢轴快速排序 | o(n²) | o(n log n) | o(n log n) | o(log n) | ✔️ | ||
| 侏儒排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 奇怪的是 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 优化的气泡排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 优化的鸡尾酒振荡器排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 优化的侏儒排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 快速排序 | o(n²) | o(n log n) | o(n log n) | o(log n) | ✔️ | ||
| 快速排序3向 | o(n²) | 在) | o(n log n) | o(log n)或o(n) | ✔️ | ||
| 稳定的快速排序 | o(n²) | o(n log n) | o(n log n) | 在) | ✔️ | ✔️ | |
| 蒂姆排序 | o(n log n) | 在) | o(n log n) | 在) | ✔️ | ||
| AVL树排序 | o(n log n) | 在) | o(n log n) | 在) | ✔️ | 在最坏的情况下,使用二进制搜索树和O(n log n)使用自平衡二进制搜索树时 | |
| 二进制插入排序 | o(n log n) | 在) | o(n log n) | o(1) | ✔️ | ✔️ | |
| 周期排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | ||
| 插入排序 | o(n²) | 在) | o(n²) | o(1) | ✔️ | ✔️ | |
| 耐心排序 | o(n log n) | 在) | o(n log n) | 在) | ✔️ | ||
| 外壳排序 | 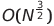 或o(nlog²n) 或o(nlog²n) | o(n log n) | o(n^1.25)至o(n²) | o(1) | ✔️ | ||
| 树排序 | o(n²) | o(n log n) | o(n log n) | 在) | ✔️ | 在最坏的情况下,使用二进制搜索树和O(n log n)使用自平衡二进制搜索树时 | |
| 自下而上的合并排序 | o(n log n) | o(n log n) | o(n log n) | 在) | ✔️ | ||
| 现场合并排序 | o(n²) | o(n²) | o(n²) | o(log n) | ✔️ | ✔️ | |
| 合并排序 | o(n log n) | o(n log n) | o(n log n) | 在) | ✔️ | ||
| Bitonic排序 | o(log²n) | o(log²n) | o(log²n) | o(nlog²n) | ✔️ | ||
| 成对网络排序 | 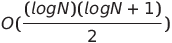 或o(n log n) 或o(n log n) | o(n log n) | o(n log n) | 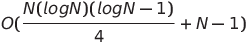 | ✔️ | 最坏的情况是使用并行时间和空间复杂性非平行时间 | |
| 水桶排序 | o(n²) | o(n+k) | o(n+k) | o(n+k) | ✔️ | k是水桶的数量 | |
| 计数排序 | o(n+k) | o(n+k) | o(n+k) | o(n+k) | ✔️ | k是输入数据的范围 | |
| 重力(珠)排序 | o(s) | o(1)或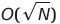 | 在) | o(n²) | ✔️ | s是数组元素的总和,o(1)不能在实践中实现 | |
| 鸽洞排序 | o(n+n) | o(n+n) | o(n+n) | o(n+n) | ✔️ | n是元素的数量, n是输入数据的范围 | |
| Radix LSD排序 | O(NW) | O(NW) | O(NW) | 在) | ✔️ | W是最大元素宽度(位) | |
| 双重选择排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | 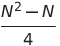 比较 比较 | |
| 最大堆排序 | o(n log n) | o(n log n) | o(n log n) | o(1) | ✔️ | ||
| 最小堆排序 | o(n log n) | o(n log n) | o(n log n) | o(1) | ✔️ | ||
| 选择排序 | o(n²) | o(n²) | o(n²) | o(1) | ✔️ | 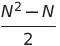 比较 比较 |