Sort_Algorithms
V1.1
실행 시간과 C 언어로 분류 알고리즘의 변동성을 보여주는 프로그램. 8 개의 다른 범주로 분산 된 48 개의 분류 알고리즘이 있습니다.
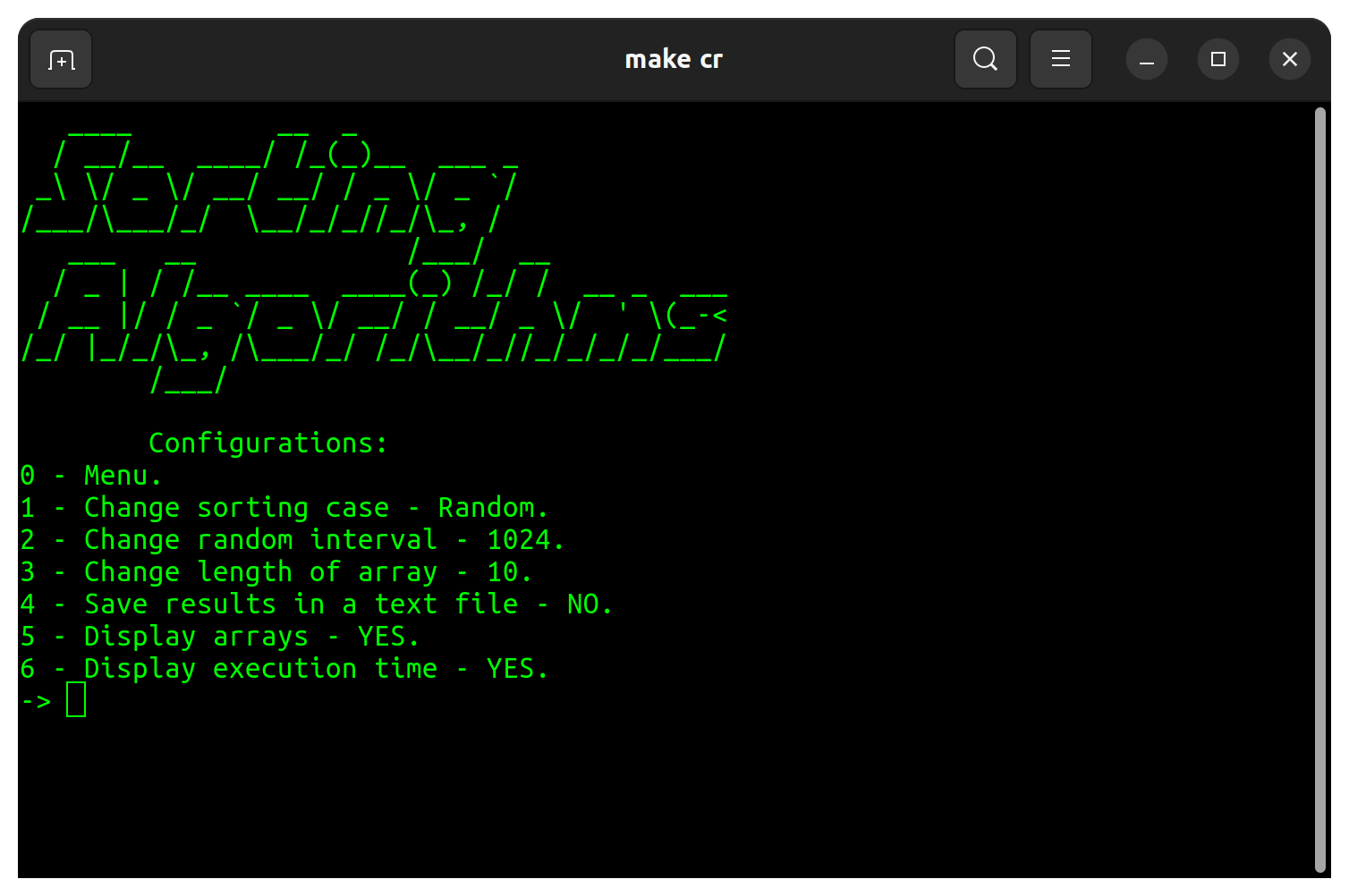
프로그램 설정에는 아래 표에 언급 된 수정 사항이 있습니다.
| 구성 | 기본 |
|---|---|
| 정렬 케이스 | 무작위의 |
| 임의의 간격 | 32 |
| 배열의 길이 | 10 |
| 텍스트 파일로 결과를 저장합니다 | 아니요 |
| 디스플레이 어레이 | 예 |
| 실행 시간을 표시합니다 | 예 |
참고 : 프로그램을 실행하려면 아래 지침을 실행하려면 컴퓨터에 GCC 컴파일러를 설치해야합니다.
터미널을 열고 프로젝트 디렉토리로 이동하십시오. 터미널에서 make 실행하면 프로그램을 컴파일 할 수 있습니다. make와 함께 실행할 수있는 명령 ( make ${command} ) :
| 명령 | 설명 |
|---|---|
| 깨끗한 | 생성 된 모든 객체를 지우십시오 |
| Cr | 컴파일하고 실행하십시오 |
| rmproper | 모든 객체 파일을 지우십시오 |
| 달리다 | 메인 프로그램을 실행하십시오 |
명령 프롬프트 또는 PowerShell에서 Project의 디렉토리로 이동하여 execute.bat 실행하십시오.
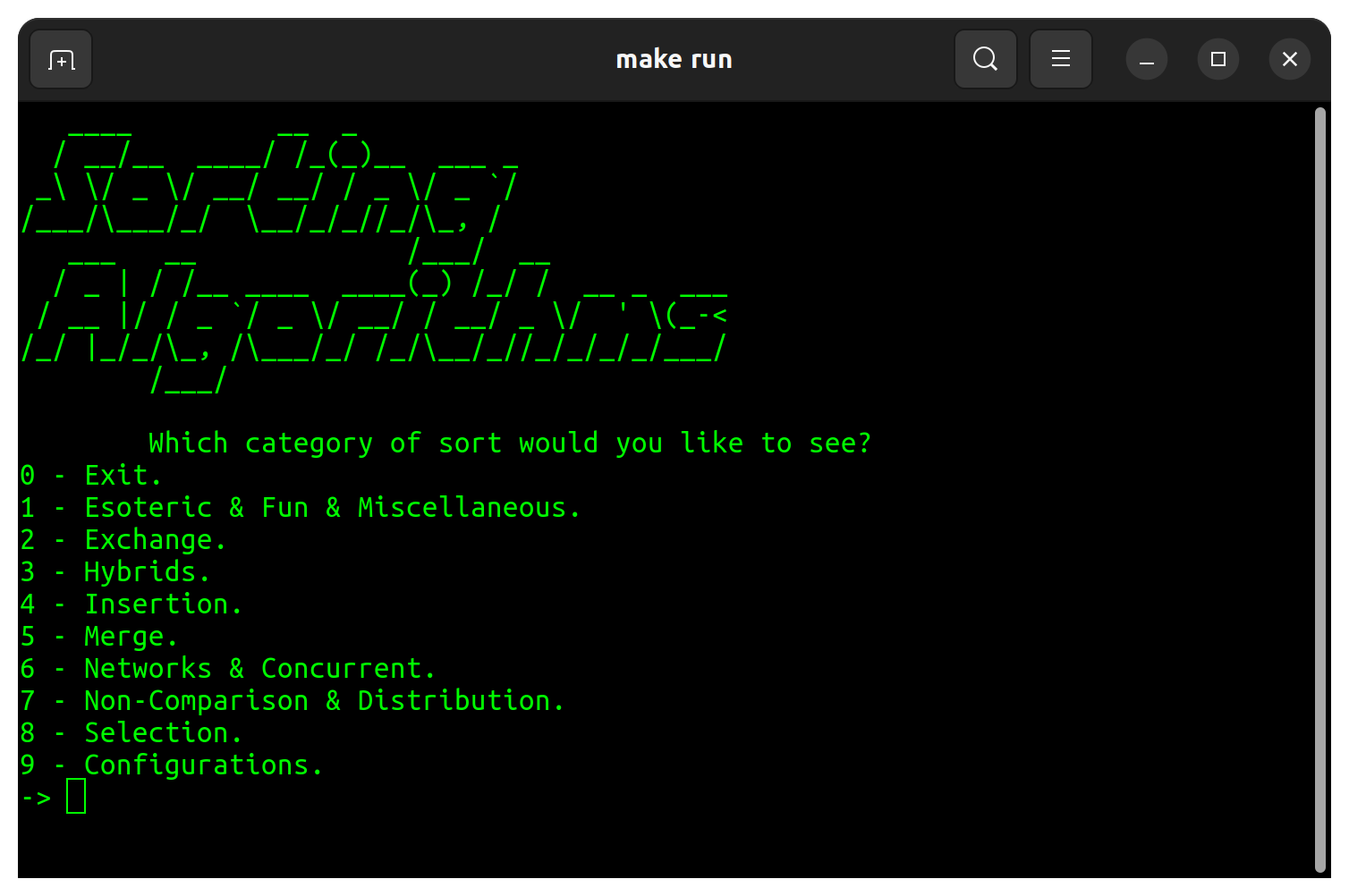
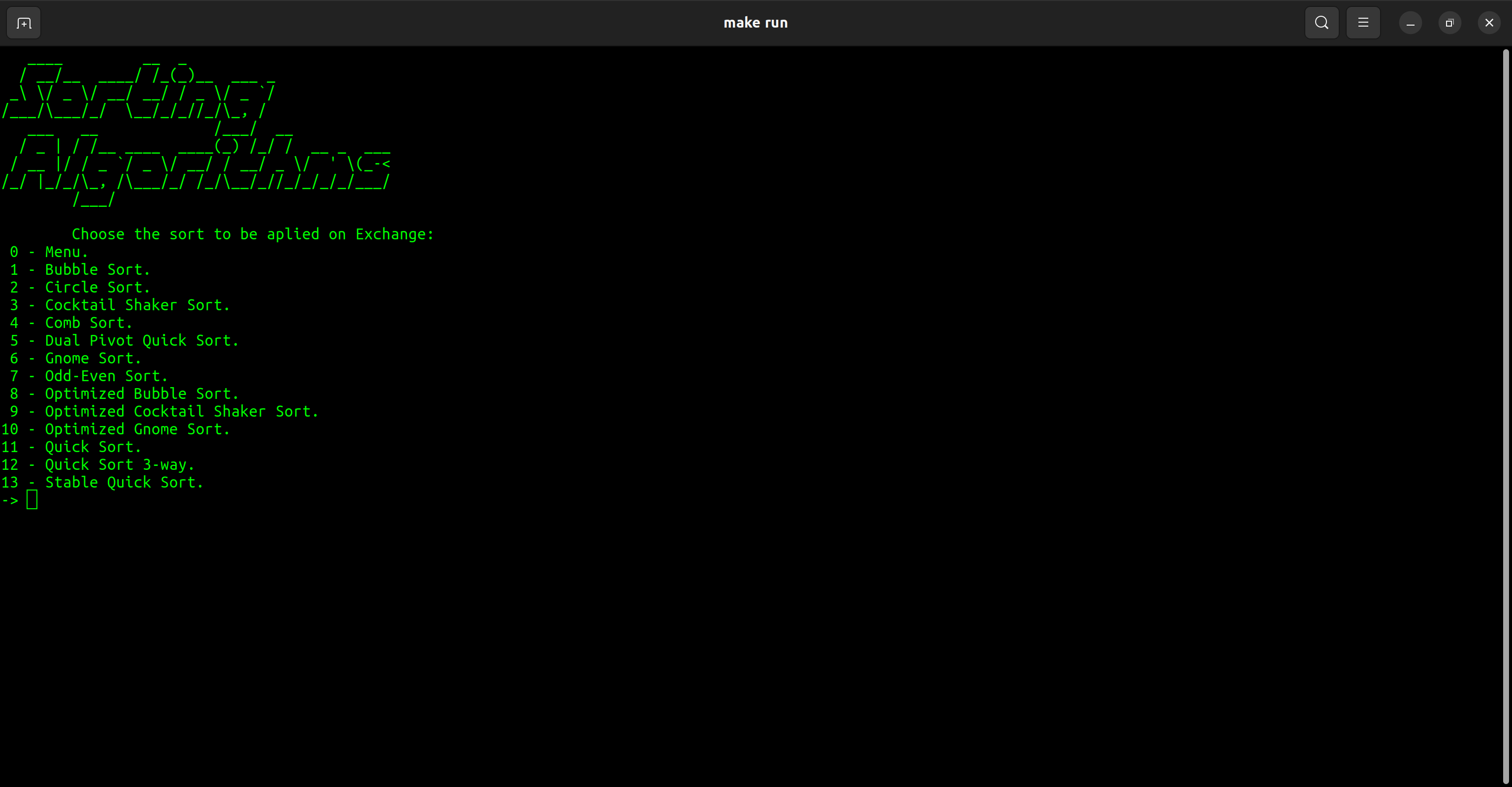
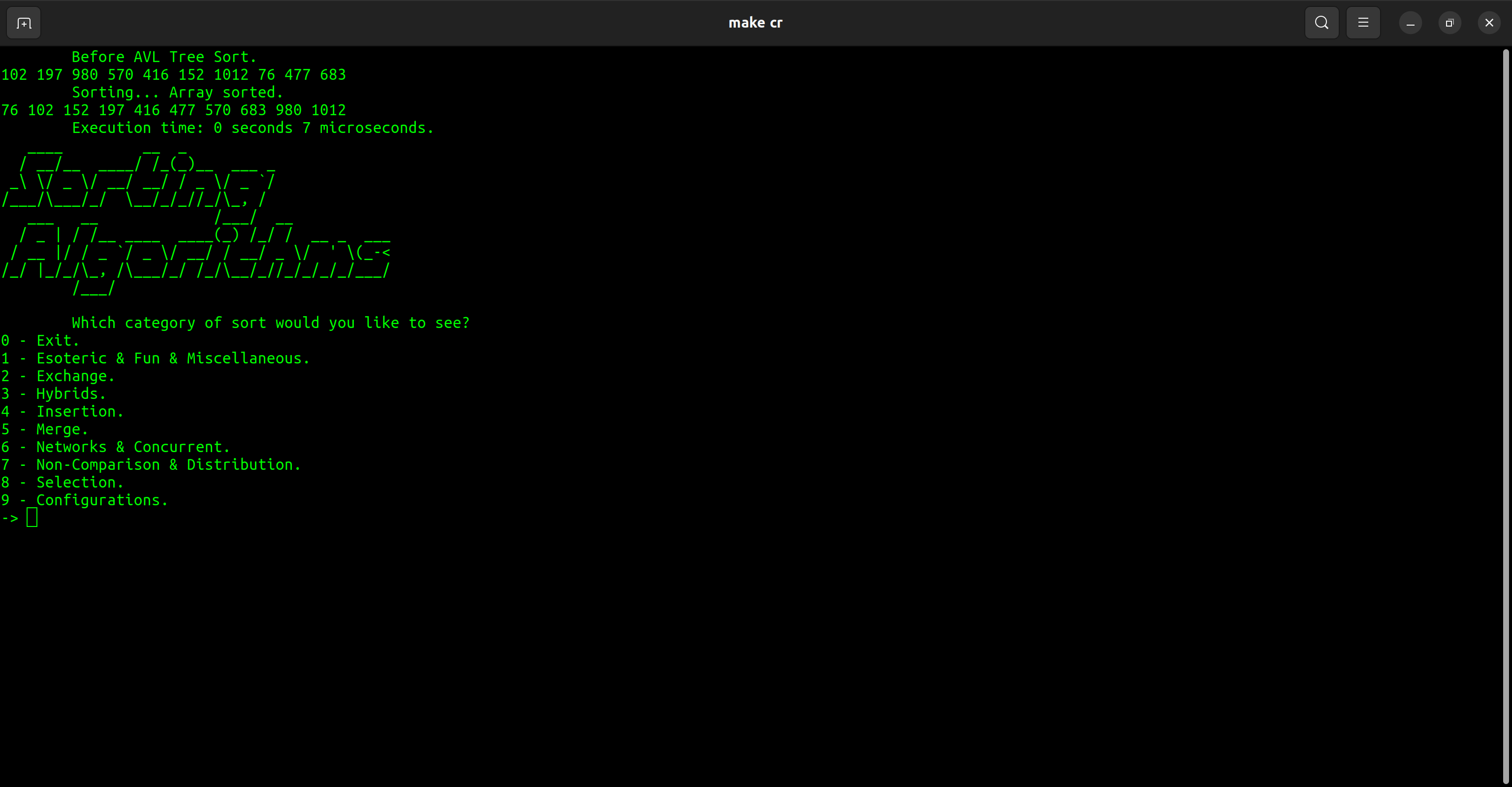
| 범주 | 종류 |
|---|---|
| 밀교 및 재미 및 기타 | 나쁜 종류 Bogo Bogo 정렬 BOGO 정렬 버블보고 정렬 칵테일보고 정렬 교환 bogo 정렬 덜 bogo 정렬 팬케이크 정렬 어리석은 정렬 수면 정렬 느린 정렬 스파게티 정렬 Stooge 정렬 |
| 교환 | 버블 정렬 원형 칵테일 셰이커 정렬 빗 정렬 듀얼 피벗 빠른 정렬 그놈 정렬 이상한 정렬 최적화 된 거품 정렬 최적화 된 칵테일 셰이커 정렬 최적화 된 그놈 정렬 빠른 정렬 빠른 정렬 3 방향 안정적인 빠른 정렬 |
| 하이브리드 | 팀 정렬 |
| 삽입 | AVL 트리 정렬 이진 삽입 정렬 사이클 정렬 삽입 정렬 인내 정렬 쉘 정렬 나무 정렬 |
| 병합 | 상향식은 정렬을 병합합니다 내부 병합 정렬 정렬을 병합하십시오 |
| 네트워크 및 동시 | Bitonic 정렬 쌍별 네트워크 정렬 |
| 비교 및 배포 | 버킷 정렬 계산 정렬 중력 (비드) 정렬 비둘기 구멍 정렬 Radix LSD 정렬 |
| 선택 | 이중 선택 정렬 최대 힙 정렬 최소 힙 정렬 선택 정렬 |
| 연산 | 최악의 경우 | 가장 좋습니다 | 평균 | 공간 복잡성 | 현장 | 안정적인 | 메모 |
|---|---|---|---|---|---|---|---|
| 나쁜 종류 | O (n³) | O (n³) | O (n³) | o (1) | ✔️ | ||
| Bogo Bogo 정렬 | O (인피니티) | O (n²) | O ((n+1)!) | o (1) | ✔️ | 무작위 조작으로 인해 최악의 경우가 무한할 수 있습니다. | |
| BOGO 정렬 | O (인피니티) | 에) | O ((n+1)!) | o (1) | ✔️ | 무작위 조작으로 인해 최악의 경우가 무한할 수 있습니다. | |
| 버블보고 정렬 | O (인피니티) | 에) | O ((n+1)!) | o (1) | ✔️ | ✔️ | 무작위 조작으로 인해 최악의 경우가 무한할 수 있습니다. |
| 칵테일보고 정렬 | O (인피니티) | 에) | O ((n+1)!) | o (1) | ✔️ | 무작위 조작으로 인해 최악의 경우가 무한할 수 있습니다. | |
| 교환 bogo 정렬 | O (인피니티) | 에) | O ((n+1)!) | o (1) | ✔️ | 무작위 조작으로 인해 최악의 경우가 무한할 수 있습니다. | |
| 덜 bogo 정렬 | O (인피니티) | O (n²) | O ((n+1)!) | o (1) | ✔️ | 무작위 조작으로 인해 최악의 경우가 무한할 수 있습니다. | |
| 팬케이크 정렬 | O (n²) | O (n²) | O (n²) | o (1) | ✔️ | ||
| 어리석은 정렬 | O (n²) | O (n²) | O (n²) | o (1) | ✔️ | ||
| 수면 정렬 | o (int_max) | o (max (입력) + n) | o (max (입력) + n) | 에) | ✔️ | CPU 스케줄러를 사용하여 정렬하십시오 | |
| 느린 정렬 | O (n*n!) | 에) | O ((n+1)!) | o (1) | ✔️ | ||
| 스파게티 정렬 | 에) | 에) | 에) | 에) | ✔️ | ||
| Stooge 정렬 |  |  |  | 에) | |||
| 버블 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 원형 | o (n log n log n) | o (n log n) | o (n log n) | o (1) | ✔️ | ||
| 칵테일 셰이커 정렬 | O (n²) | O (n²) | O (n²) | o (1) | ✔️ | ✔️ | |
| 빗 정렬 | O (n²) | o (n log n) | 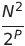 | o (1) | ✔️ | P 는 증분 수입니다 | |
| 듀얼 피벗 빠른 정렬 | O (n²) | o (n log n) | o (n log n) | O (로그 N) | ✔️ | ||
| 그놈 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 이상한 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 최적화 된 거품 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 최적화 된 칵테일 셰이커 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 최적화 된 그놈 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 빠른 정렬 | O (n²) | o (n log n) | o (n log n) | O (로그 N) | ✔️ | ||
| 빠른 정렬 3 방향 | O (n²) | 에) | o (n log n) | O (로그 N) 또는 O (N) | ✔️ | ||
| 안정적인 빠른 정렬 | O (n²) | o (n log n) | o (n log n) | 에) | ✔️ | ✔️ | |
| 팀 정렬 | o (n log n) | 에) | o (n log n) | 에) | ✔️ | ||
| AVL 트리 정렬 | o (n log n) | 에) | o (n log n) | 에) | ✔️ | 최악의 경우, 이진 검색 트리와 O (n log n)를 사용할 때 o (n²) 자체 균형 이진 검색 트리를 사용할 때 | |
| 이진 삽입 정렬 | o (n log n) | 에) | o (n log n) | o (1) | ✔️ | ✔️ | |
| 사이클 정렬 | O (n²) | O (n²) | O (n²) | o (1) | ✔️ | ||
| 삽입 정렬 | O (n²) | 에) | O (n²) | o (1) | ✔️ | ✔️ | |
| 인내 정렬 | o (n log n) | 에) | o (n log n) | 에) | ✔️ | ||
| 쉘 정렬 | 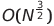 또는 O (n log² n) 또는 O (n log² n) | o (n log n) | o (n^1.25) ~ O (n²) | o (1) | ✔️ | ||
| 나무 정렬 | O (n²) | o (n log n) | o (n log n) | 에) | ✔️ | 최악의 경우, 이진 검색 트리와 O (n log n)를 사용할 때 o (n²) 자체 균형 이진 검색 트리를 사용할 때 | |
| 상향식은 정렬을 병합합니다 | o (n log n) | o (n log n) | o (n log n) | 에) | ✔️ | ||
| 내부 병합 정렬 | O (n²) | O (n²) | O (n²) | O (로그 N) | ✔️ | ✔️ | |
| 정렬을 병합하십시오 | o (n log n) | o (n log n) | o (n log n) | 에) | ✔️ | ||
| Bitonic 정렬 | O (log² n) | O (log² n) | O (log² n) | O (n log² n) | ✔️ | ||
| 쌍별 네트워크 정렬 | 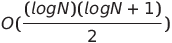 또는 O (n log n) 또는 O (n log n) | o (n log n) | o (n log n) | 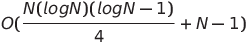 | ✔️ | 최악의 경우는 평행 시간과 공간 복잡성을 사용하고 있습니다. | |
| 버킷 정렬 | O (n²) | O (N+K) | O (N+K) | O (N+K) | ✔️ | K 는 버킷 수입니다 | |
| 계산 정렬 | O (N+K) | O (N+K) | O (N+K) | O (N+K) | ✔️ | K 는 입력 데이터의 범위입니다 | |
| 중력 (비드) 정렬 | O (s) | o (1) 또는 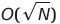 | 에) | O (n²) | ✔️ | S 는 배열 요소의 합입니다. O (1)는 실제로 구현할 수 없습니다. | |
| 비둘기 구멍 정렬 | O (N+N) | O (N+N) | O (N+N) | O (N+N) | ✔️ | n 은 요소 수이고 n은 입력 데이터의 범위입니다. | |
| Radix LSD 정렬 | O (NW) | O (NW) | O (NW) | 에) | ✔️ | w 는 Maxumum 요소 너비 (비트)입니다. | |
| 이중 선택 정렬 | O (n²) | O (n²) | O (n²) | o (1) | ✔️ | 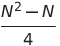 비교 비교 | |
| 최대 힙 정렬 | o (n log n) | o (n log n) | o (n log n) | o (1) | ✔️ | ||
| 최소 힙 정렬 | o (n log n) | o (n log n) | o (n log n) | o (1) | ✔️ | ||
| 선택 정렬 | O (n²) | O (n²) | O (n²) | o (1) | ✔️ | 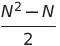 비교 비교 |