Sort_Algorithms
V1.1
Un programa para mostrar el tiempo de ejecución y la variabilidad de clasificar los algoritmos en el lenguaje C Hay 48 algoritmos de clasificación avalables distribuidos en 8 categorías diferentes.
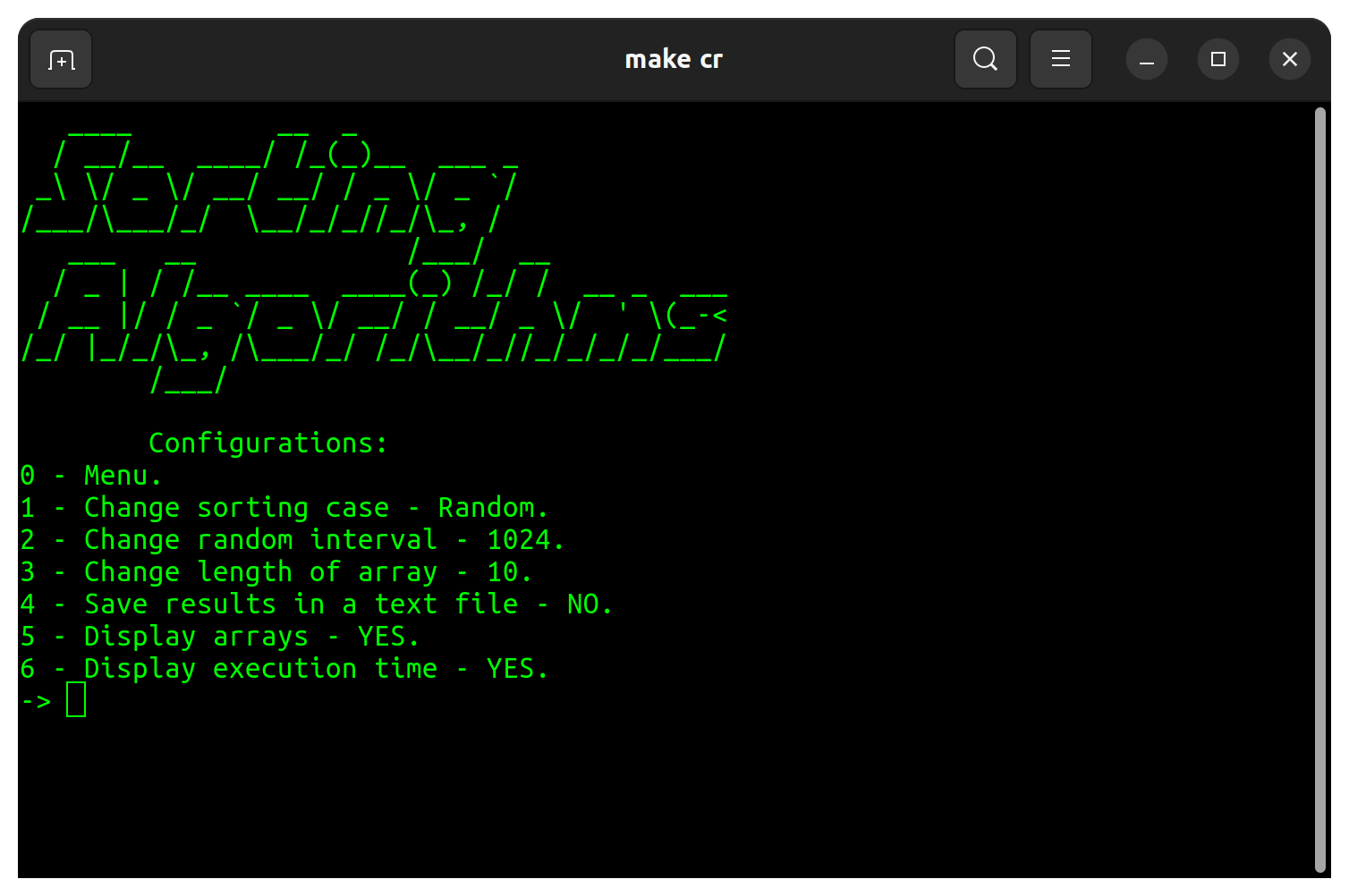
En la configuración del programa, hay modificaciones avalables en la tabla a continuación:
| Configuración | Por defecto |
|---|---|
| Caso de clasificación | Aleatorio |
| Intervalo aleatorio | 32 |
| Longitud de matriz | 10 |
| Guardar resultados en un archivo de texto | NO |
| Mostrar matrices | SÍ |
| Mostrar tiempo de ejecución | SÍ |
Nota: Debe tener instalado el compilador GCC en su máquina para ejecutar las instrucciones a continuación para ejecutar el programa.
Abra una terminal y vaya al directorio del proyecto. Ejecutar make en Terminal Permitir compilar el programa. Comandos avalables para ejecutar con make ( make ${command} )::
| Dominio | Descripción |
|---|---|
| limpio | Borrar todos los objetos generados |
| CR | Compilar y ejecutar |
| rmproper | Borrar todos los archivos de objetos |
| correr | Ejecutar el programa principal |
En el símbolo del sistema o PowerShell y vaya al directorio del proyecto y ejecute execute.bat .
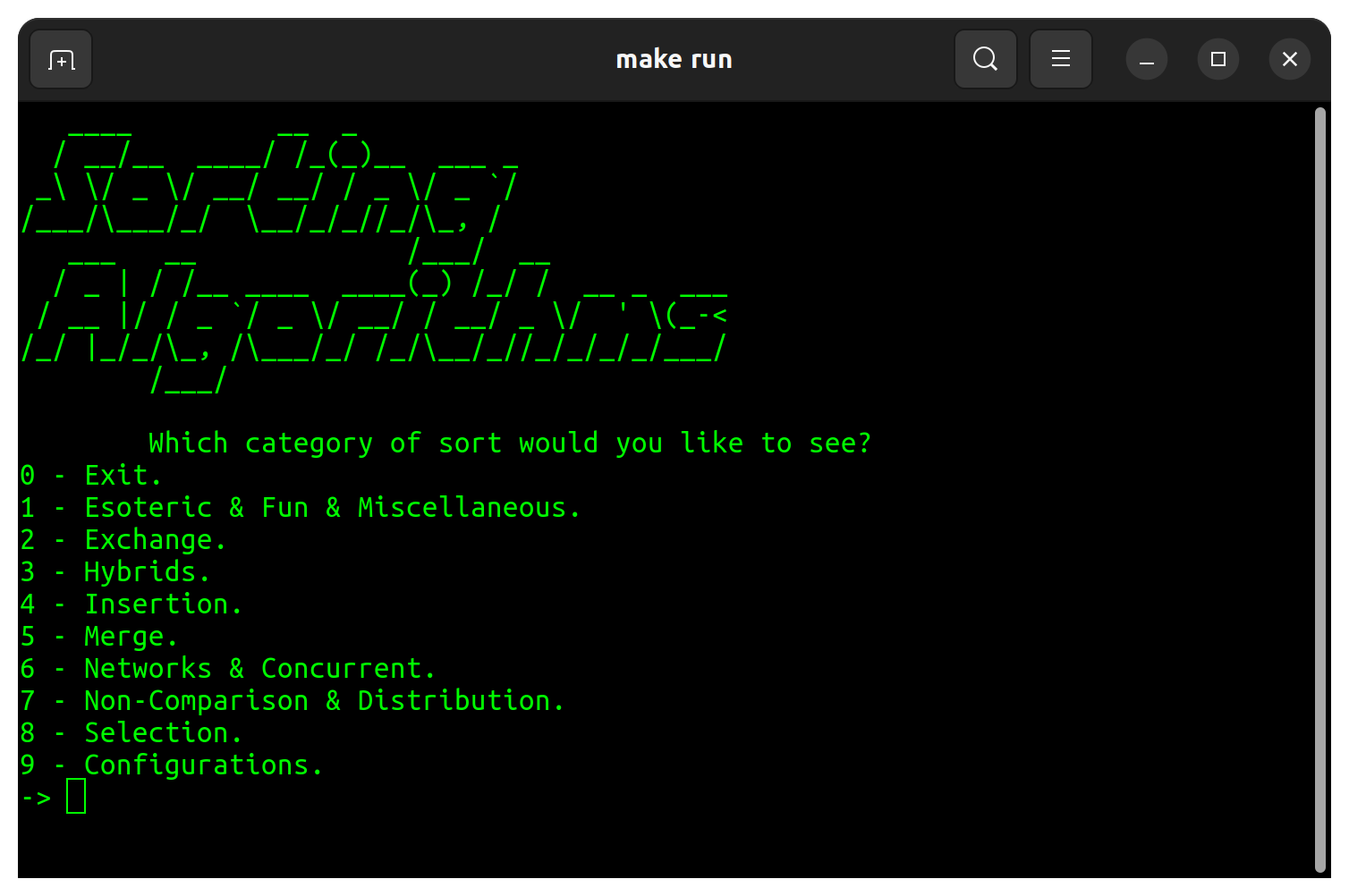
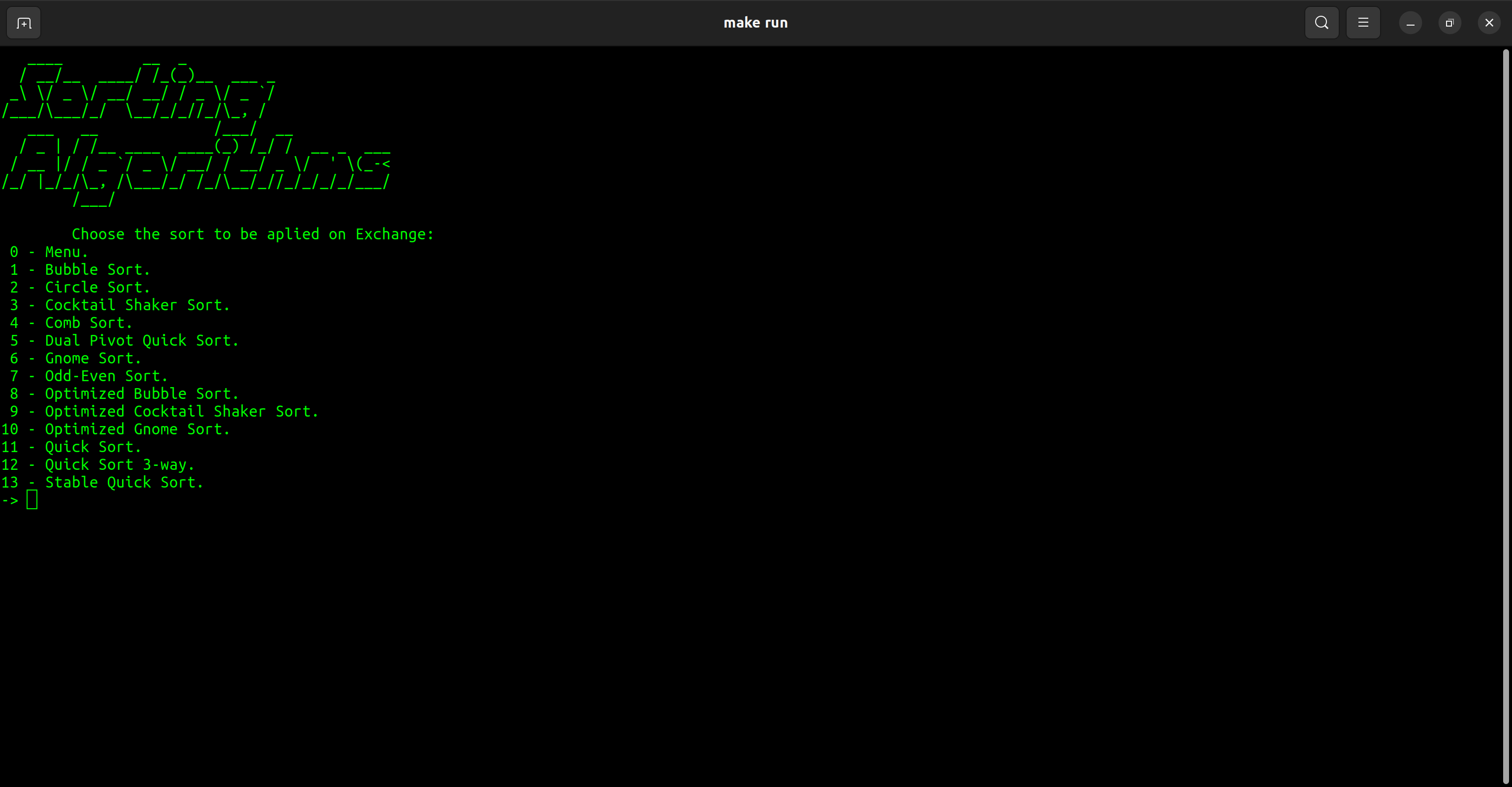
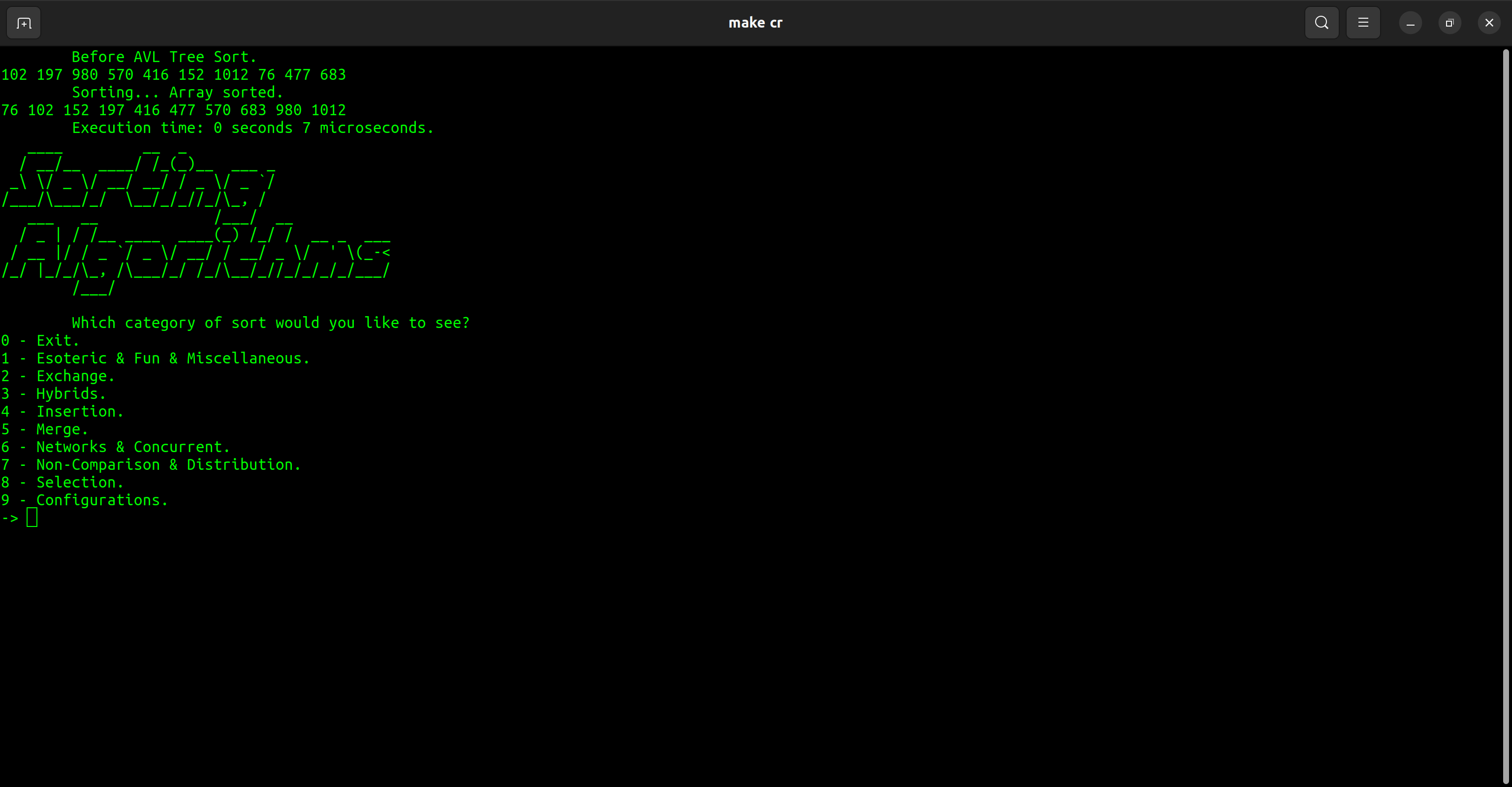
| Categoría | Clasificar |
|---|---|
| Esotérico y diversión y misceláneo | Malo Bogo bogo sort Bogo sort Bubble Bogo Sort Cóctel bogo sort Exchange bogo sort Menos clasificación de Bogo Clasificación de panqueques Tipo tonto Sorteo de sueño Clasificación lenta Spaghetti Sort STOOGE SUPER |
| Intercambio | Burbuja Ortográfico Sorteo de cócteles Ordenar Dual pivote Sort de gnomo Orden de incluso incluso Clasificación de burbujas optimizada Sorteo de cócteles optimizado Clasificación de gnomo optimizado Clasificación rápida Sort Rápido 3 vías Estable clasificación rápida |
| Híbridos | Tim sort |
| Inserción | Clasificación de árbol AVL Clasificación de inserción binaria Clasificación de ciclo Clasificación de inserción Clasificación de paciencia Clasificar con cáscara Ordena de árboles |
| Unir | Clasificación de fusión de abajo hacia arriba Clasificación de fusión en el lugar Fusionar |
| Redes y concurrentes | Bitónico Clasificación de red por pares |
| No comparación y distribución | Clasificación de cubos Clasificación de contabilidad Gravedad (Bead) Sorteo Clasificación de paloma Radix lsd sort |
| Selección | Clasificación de doble selección Sort de montón máximo Mindade sort Clasificación de selección |
| Algoritmo | Peor de los casos | Mejor caso | Promedio | Complejidad espacial | En el lugar | Estable | Notas |
|---|---|---|---|---|---|---|---|
| Malo | O (n³) | O (n³) | O (n³) | O (1) | ✔️ | ||
| Bogo bogo sort | O (infinito) | O (n²) | O ((n+1)!) | O (1) | ✔️ | El peor de los casos puede ser ilimitado debido a la manipulación aleatoria | |
| Bogo sort | O (infinito) | EN) | O ((n+1)!) | O (1) | ✔️ | El peor de los casos puede ser ilimitado debido a la manipulación aleatoria | |
| Bubble Bogo Sort | O (infinito) | EN) | O ((n+1)!) | O (1) | ✔️ | ✔️ | El peor de los casos puede ser ilimitado debido a la manipulación aleatoria |
| Cóctel bogo sort | O (infinito) | EN) | O ((n+1)!) | O (1) | ✔️ | El peor de los casos puede ser ilimitado debido a la manipulación aleatoria | |
| Exchange bogo sort | O (infinito) | EN) | O ((n+1)!) | O (1) | ✔️ | El peor de los casos puede ser ilimitado debido a la manipulación aleatoria | |
| Menos clasificación de Bogo | O (infinito) | O (n²) | O ((n+1)!) | O (1) | ✔️ | El peor de los casos puede ser ilimitado debido a la manipulación aleatoria | |
| Clasificación de panqueques | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Tipo tonto | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Sorteo de sueño | O (int_max) | O (max (entrada) + n) | O (max (entrada) + n) | EN) | ✔️ | Tomemos el uso del planificador de CPU para clasificar | |
| Clasificación lenta | O (N*n!) | EN) | O ((n+1)!) | O (1) | ✔️ | ||
| Spaghetti Sort | EN) | EN) | EN) | EN) | ✔️ | ||
| STOOGE SUPER |  |  |  | EN) | |||
| Burbuja | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Ortográfico | O (n log n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Sorteo de cócteles | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ✔️ | |
| Ordenar | O (n²) | O (n log n) | 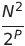 | O (1) | ✔️ | P es el número de incrementos | |
| Dual pivote | O (n²) | O (n log n) | O (n log n) | O (log n) | ✔️ | ||
| Sort de gnomo | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Orden de incluso incluso | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Clasificación de burbujas optimizada | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Sorteo de cócteles optimizado | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Clasificación de gnomo optimizado | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Clasificación rápida | O (n²) | O (n log n) | O (n log n) | O (log n) | ✔️ | ||
| Sort Rápido 3 vías | O (n²) | EN) | O (n log n) | O (log n) o o (n) | ✔️ | ||
| Estable clasificación rápida | O (n²) | O (n log n) | O (n log n) | EN) | ✔️ | ✔️ | |
| Tim sort | O (n log n) | EN) | O (n log n) | EN) | ✔️ | ||
| Clasificación de árbol AVL | O (n log n) | EN) | O (n log n) | EN) | ✔️ | En el peor de los casos, o (n²) cuando se usa el árbol de búsqueda binario y o (n log n) cuando se usa el árbol de búsqueda binario auto-equilibrado | |
| Clasificación de inserción binaria | O (n log n) | EN) | O (n log n) | O (1) | ✔️ | ✔️ | |
| Clasificación de ciclo | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Clasificación de inserción | O (n²) | EN) | O (n²) | O (1) | ✔️ | ✔️ | |
| Clasificación de paciencia | O (n log n) | EN) | O (n log n) | EN) | ✔️ | ||
| Clasificar con cáscara | 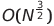 o o (n log² n) o o (n log² n) | O (n log n) | O (n^1.25) a o (n²) | O (1) | ✔️ | ||
| Ordena de árboles | O (n²) | O (n log n) | O (n log n) | EN) | ✔️ | En el peor de los casos, o (n²) cuando se usa el árbol de búsqueda binario y o (n log n) cuando se usa el árbol de búsqueda binario auto-equilibrado | |
| Clasificación de fusión de abajo hacia arriba | O (n log n) | O (n log n) | O (n log n) | EN) | ✔️ | ||
| Clasificación de fusión en el lugar | O (n²) | O (n²) | O (n²) | O (log n) | ✔️ | ✔️ | |
| Fusionar | O (n log n) | O (n log n) | O (n log n) | EN) | ✔️ | ||
| Bitónico | O (log² n) | O (log² n) | O (log² n) | O (n log² n) | ✔️ | ||
| Clasificación de red por pares | 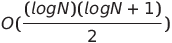 o o (n log n) o o (n log n) | O (n log n) | O (n log n) | 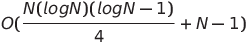 | ✔️ | El peor de los casos es usar tiempo paralelo y complejidad del espacio no paralelo | |
| Clasificación de cubos | O (n²) | O (N+K) | O (N+K) | O (N+K) | ✔️ | k es el número de cubos | |
| Clasificación de contabilidad | O (N+K) | O (N+K) | O (N+K) | O (N+K) | ✔️ | k es el rango de datos de entrada | |
| Gravedad (Bead) Sorteo | O (s) | O (1) o 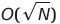 | EN) | O (n²) | ✔️ | S es la suma de los elementos de matriz, o (1) no se puede implementar en la práctica | |
| Clasificación de paloma | O (N+N) | O (N+N) | O (N+N) | O (N+N) | ✔️ | N es el número de elementos y n es el rango de datos de entrada | |
| Radix lsd sort | O (NW) | O (NW) | O (NW) | EN) | ✔️ | W es el ancho del elemento maxumum (bits) | |
| Clasificación de doble selección | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | 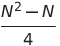 Comparaciones Comparaciones | |
| Sort de montón máximo | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Mindade sort | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Clasificación de selección | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | 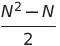 Comparaciones Comparaciones |