Sort_Algorithms
V1.1
Программа, показывающая время исполнения и переменную переменную алгоритмы сортировки на языке C Существует 48 алгоритмов сортировки, распределенных в 8 различных категориях.
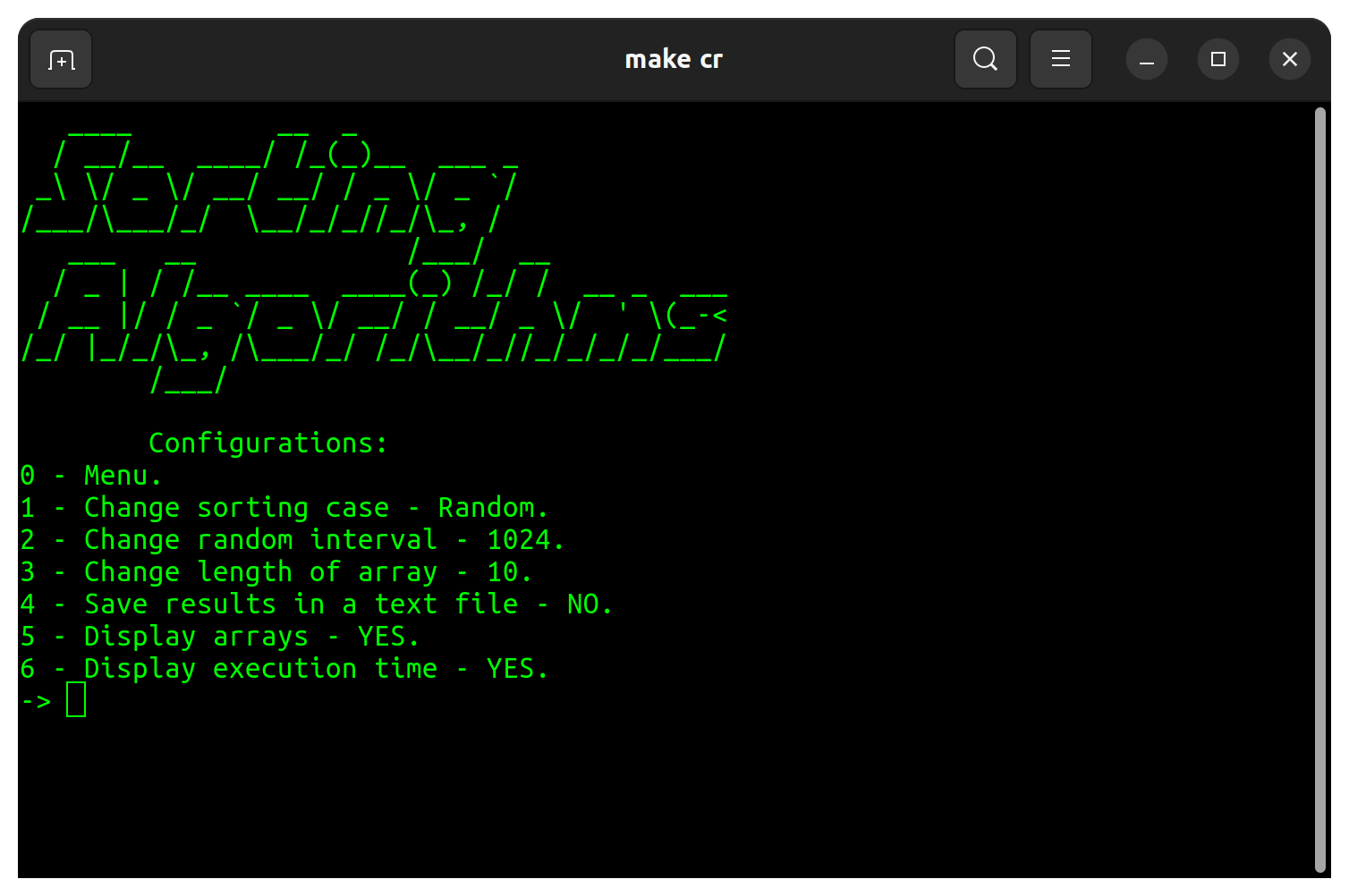
В настройках программы есть доступные модификации, отмеченные в таблице ниже:
| Конфигурация | По умолчанию |
|---|---|
| Сортировка | Случайный |
| Случайный интервал | 32 |
| Длина массива | 10 |
| Сохранить результаты в текстовом файле | НЕТ |
| Отображение массивов | ДА |
| Отображение времени выполнения | ДА |
Примечание. Вам необходимо установить компилятор GCC в вашем компьютере, чтобы выполнить инструкции ниже, чтобы запустить программу.
Откройте терминал и перейдите в каталог проекта. Выполнить make в терминале позволить компилировать программу. Команды доступны для выполнения с помощью make ( make ${command} ):
| Командование | Описание |
|---|---|
| чистый | Очистить все сгенерированные объекты |
| герметичный | Скомпилируйте и бегите |
| RMProper | Очистить все объектные файлы |
| бегать | Выполнить основную программу |
В командной строке или PowerShell и перейдите в каталог Project и execute.bat .
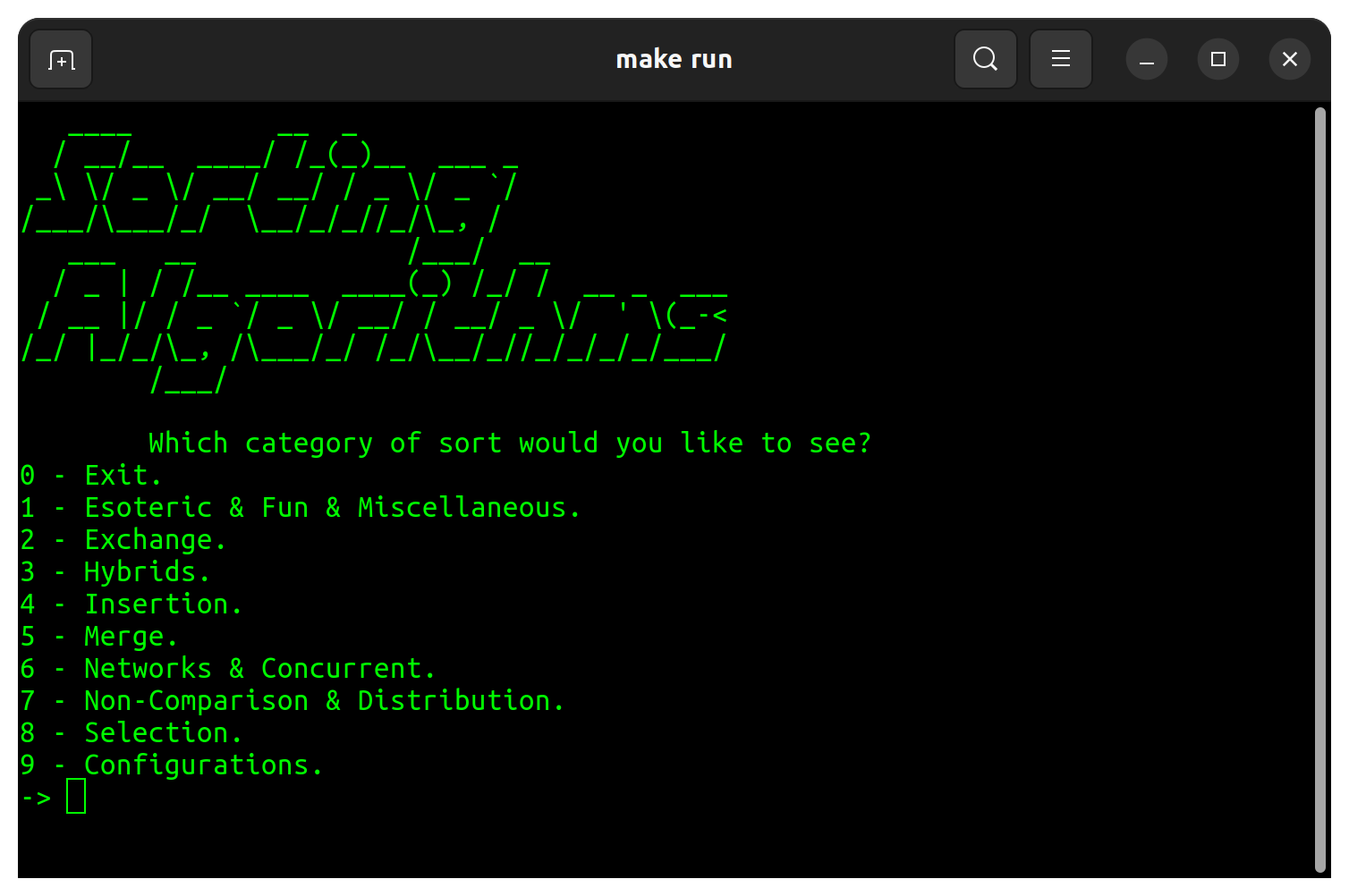
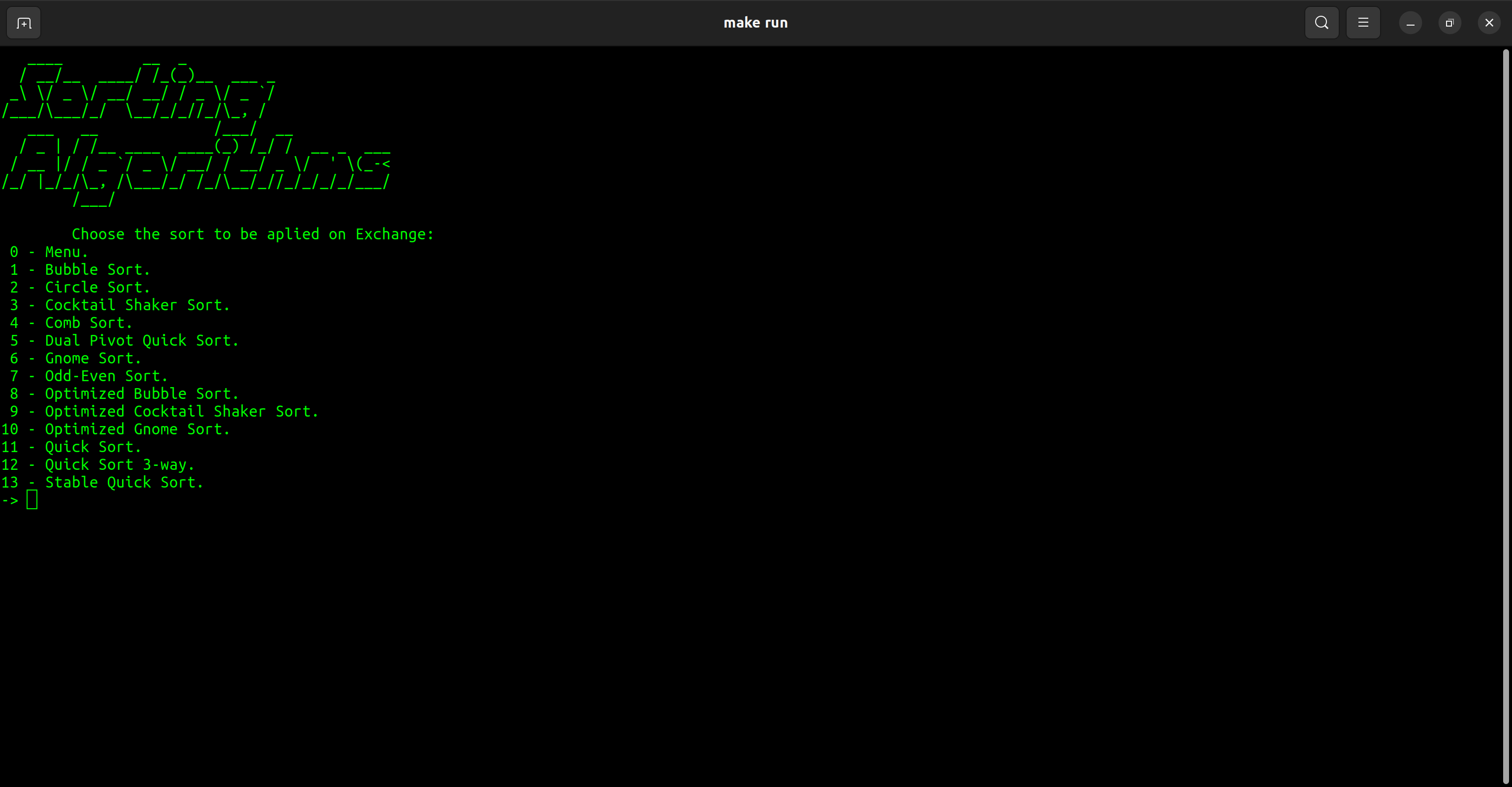
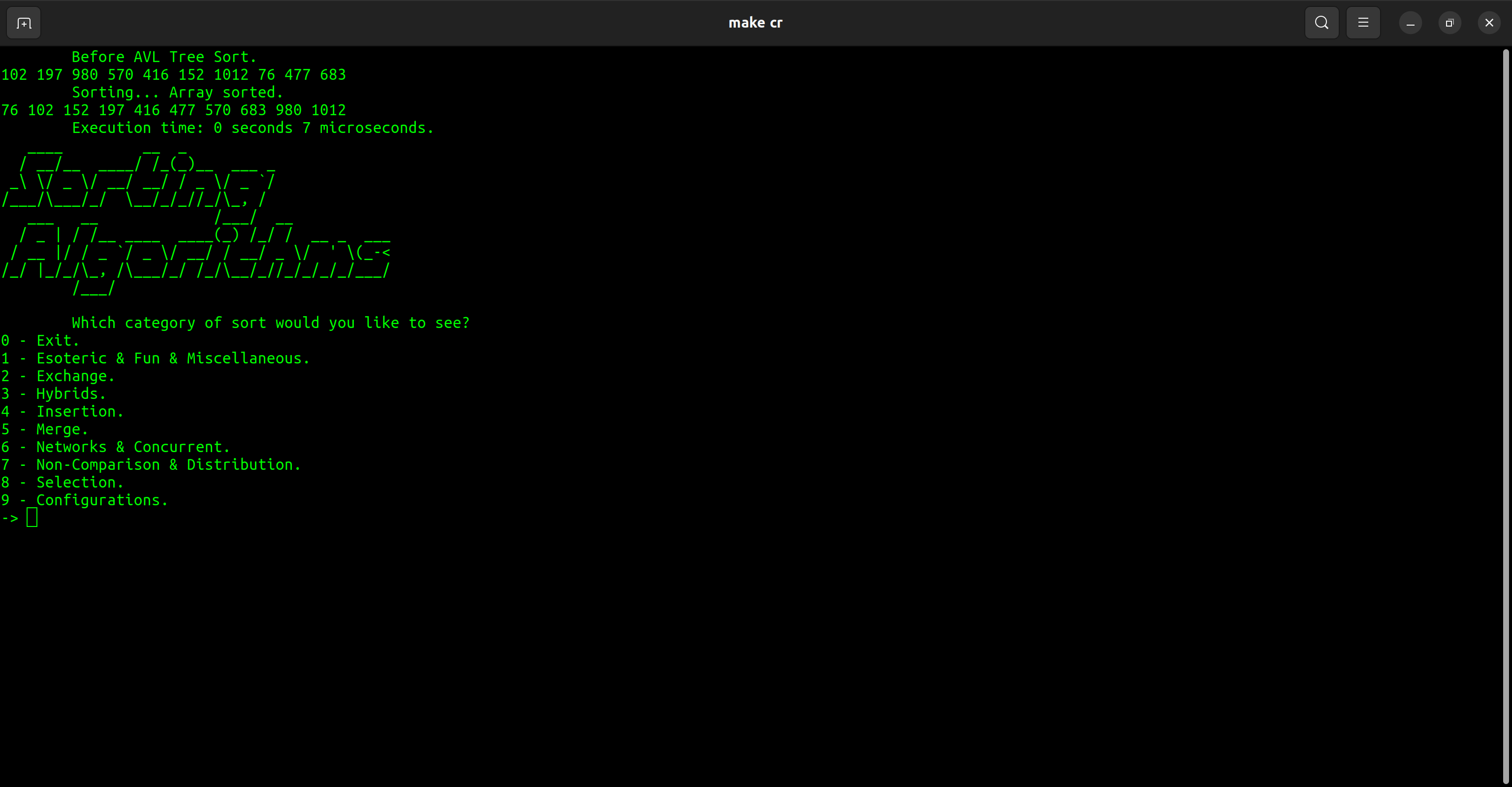
| Категория | Сортировка |
|---|---|
| Эзотерический и веселый и разнообразный | Плохой вид Бого Бого Сорт Бого, сортируем Пузырьковой сортировка Коктейль Бого Сорт Обмен Бого Сорт Меньше бого сортировки Блин Глупый вид Сон Медленный сортировка Сорта спагетти Сортировка сорта |
| Обмен | Пузырьковые сортировки Круговой сортировка Коктейльный шейкер Сортировка расчески Двойной шар Сорт Гнома Сторонний сортировка Оптимизированная пузырька Оптимизированный сортировка коктейля Оптимизированный гноме Быстрый сортировка Быстрый сортировка 3-й Стабильный быстрый сортировка |
| Гибриды | Тим Сорт |
| Вставка | AVL ДЕРЕВЫЕ Сорт Бинарная вставка Цикл Вставка сортировки Терпение Shell Sort Деревья |
| Слияние | Снизу вверх Сорт На месте слияние Слияние сортировки |
| Сети и одновременно | Битуническое сортирование Парная сеть сортировки |
| Несоответствие и распределение | Ведро сортировка Счет Гравитация (бус) сортировка Голубь Radix LSD Sort |
| Выбор | Двойной выбор Максимальная куча сортировки Миш куча сортировки Выбор сортировки |
| Алгоритм | Худший случай | Лучший случай | Средний | Сложность пространства | На месте | Стабильный | Примечания |
|---|---|---|---|---|---|---|---|
| Плохой вид | O (N ним) | O (N ним) | O (N ним) | O (1) | ✔ | ||
| Бого Бого Сорт | O (бесконечность) | O (N²) | O ((n+1)!) | O (1) | ✔ | Худший случай может быть неограничен из -за случайных манипуляций | |
| Бого, сортируем | O (бесконечность) | НА) | O ((n+1)!) | O (1) | ✔ | Худший случай может быть неограничен из -за случайных манипуляций | |
| Пузырьковой сортировка | O (бесконечность) | НА) | O ((n+1)!) | O (1) | ✔ | ✔ | Худший случай может быть неограничен из -за случайных манипуляций |
| Коктейль Бого Сорт | O (бесконечность) | НА) | O ((n+1)!) | O (1) | ✔ | Худший случай может быть неограничен из -за случайных манипуляций | |
| Обмен Бого Сорт | O (бесконечность) | НА) | O ((n+1)!) | O (1) | ✔ | Худший случай может быть неограничен из -за случайных манипуляций | |
| Меньше бого сортировки | O (бесконечность) | O (N²) | O ((n+1)!) | O (1) | ✔ | Худший случай может быть неограничен из -за случайных манипуляций | |
| Блин | O (N²) | O (N²) | O (N²) | O (1) | ✔ | ||
| Глупый вид | O (N²) | O (N²) | O (N²) | O (1) | ✔ | ||
| Сон | O (int_max) | O (max (вход) + n) | O (max (вход) + n) | НА) | ✔ | Используйте планировщик процессора, чтобы сортировать | |
| Медленный сортировка | O (n*n!) | НА) | O ((n+1)!) | O (1) | ✔ | ||
| Сорта спагетти | НА) | НА) | НА) | НА) | ✔ | ||
| Сортировка сорта |  |  |  | НА) | |||
| Пузырьковые сортировки | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Круговой сортировка | O (n log n log n) | O (n log n) | O (n log n) | O (1) | ✔ | ||
| Коктейльный шейкер | O (N²) | O (N²) | O (N²) | O (1) | ✔ | ✔ | |
| Сортировка расчески | O (N²) | O (n log n) | 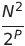 | O (1) | ✔ | P - количество приращений | |
| Двойной шар | O (N²) | O (n log n) | O (n log n) | O (log n) | ✔ | ||
| Сорт Гнома | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Сторонний сортировка | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Оптимизированная пузырька | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Оптимизированный сортировка коктейля | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Оптимизированный гноме | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Быстрый сортировка | O (N²) | O (n log n) | O (n log n) | O (log n) | ✔ | ||
| Быстрый сортировка 3-й | O (N²) | НА) | O (n log n) | O (log n) или O (n) | ✔ | ||
| Стабильный быстрый сортировка | O (N²) | O (n log n) | O (n log n) | НА) | ✔ | ✔ | |
| Тим Сорт | O (n log n) | НА) | O (n log n) | НА) | ✔ | ||
| AVL ДЕРЕВЫЕ Сорт | O (n log n) | НА) | O (n log n) | НА) | ✔ | В худшем случае O (N²) при использовании бинарного дерева поиска и O (n log n) при использовании самостоятельного бинарного дерева поиска | |
| Бинарная вставка | O (n log n) | НА) | O (n log n) | O (1) | ✔ | ✔ | |
| Цикл | O (N²) | O (N²) | O (N²) | O (1) | ✔ | ||
| Вставка сортировки | O (N²) | НА) | O (N²) | O (1) | ✔ | ✔ | |
| Терпение | O (n log n) | НА) | O (n log n) | НА) | ✔ | ||
| Shell Sort | 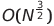 или O (n log² n) или O (n log² n) | O (n log n) | O (n^1.25) до O (n²) | O (1) | ✔ | ||
| Деревья | O (N²) | O (n log n) | O (n log n) | НА) | ✔ | В худшем случае O (N²) при использовании бинарного дерева поиска и O (n log n) при использовании самостоятельного бинарного дерева поиска | |
| Снизу вверх Сорт | O (n log n) | O (n log n) | O (n log n) | НА) | ✔ | ||
| На месте слияние | O (N²) | O (N²) | O (N²) | O (log n) | ✔ | ✔ | |
| Слияние сортировки | O (n log n) | O (n log n) | O (n log n) | НА) | ✔ | ||
| Битуническое сортирование | O (log² n) | O (log² n) | O (log² n) | O (n log² n) | ✔ | ||
| Парная сеть сортировки | 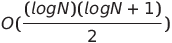 или O (n log n) или O (n log n) | O (n log n) | O (n log n) | 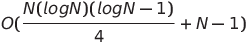 | ✔ | В худшем случае используется параллельное время и сложность пространства непараллельное время | |
| Ведро сортировка | O (N²) | O (n+k) | O (n+k) | O (n+k) | ✔ | k - это количество ведра | |
| Счет | O (n+k) | O (n+k) | O (n+k) | O (n+k) | ✔ | k - это диапазон входных данных | |
| Гравитация (бус) сортировка | O (s) | O (1) или 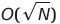 | НА) | O (N²) | ✔ | S - сумма элементов массива, O (1) не может быть реализована на практике | |
| Голубь | O (n+n) | O (n+n) | O (n+n) | O (n+n) | ✔ | N - количество элементов, а n - диапазон входных данных | |
| Radix LSD Sort | O (NW) | O (NW) | O (NW) | НА) | ✔ | W - ширина элемента максимального элемента (биты) | |
| Двойной выбор | O (N²) | O (N²) | O (N²) | O (1) | ✔ | 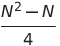 Сравнения Сравнения | |
| Максимальная куча сортировки | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔ | ||
| Миш куча сортировки | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔ | ||
| Выбор сортировки | O (N²) | O (N²) | O (N²) | O (1) | ✔ | 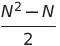 Сравнения Сравнения |