Sort_Algorithms
V1.1
C言語でのソートアルゴリズムの実行時間と変数を示すプログラム。 8つの異なるカテゴリに分散されている48のソートアルゴリズムがあります。
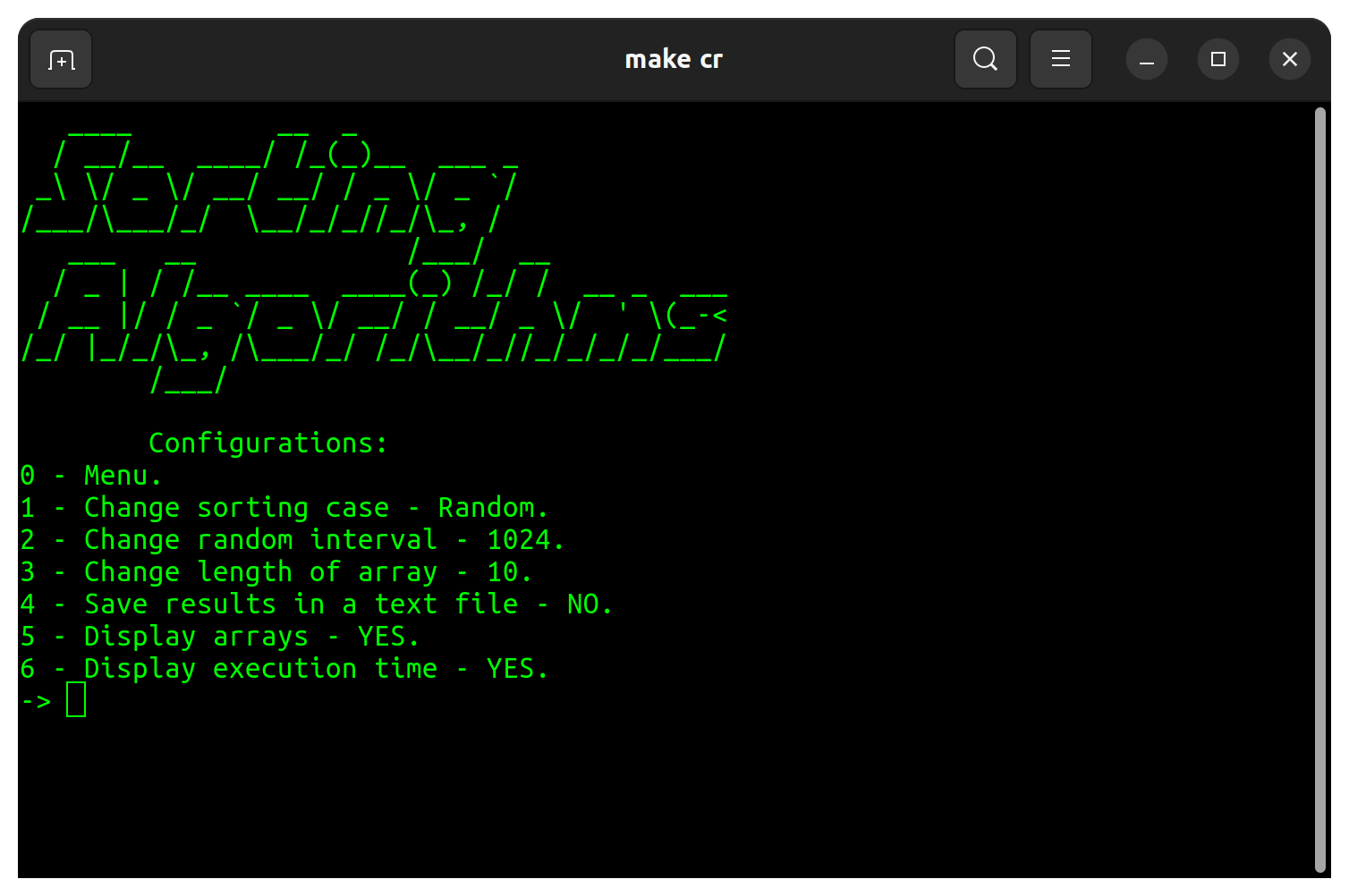
プログラムの設定には、以下の表に記載されている利用可能な変更があります。
| 構成 | デフォルト |
|---|---|
| ソートケース | ランダム |
| ランダム間隔 | 32 |
| 配列の長さ | 10 |
| テキストファイルに結果を保存します | いいえ |
| アレイを表示します | はい |
| 実行時間を表示します | はい |
注:GCCコンパイラをマシンにインストールして、以下の指示を実行してプログラムを実行する必要があります。
端末を開き、Projectのディレクトリに移動します。ターミナルでmakeを実行して、プログラムをコンパイルします。 make( make ${command} )で実行できるコマンド:
| 指示 | 説明 |
|---|---|
| クリーン | 生成されたすべてのオブジェクトをクリアします |
| cr | コンパイルして実行します |
| rmproper | すべてのオブジェクトファイルをクリアします |
| 走る | メインプログラムを実行します |
コマンドプロンプトまたはPowerShellで、Projectのディレクトリに移動してexecute.batを実行します。
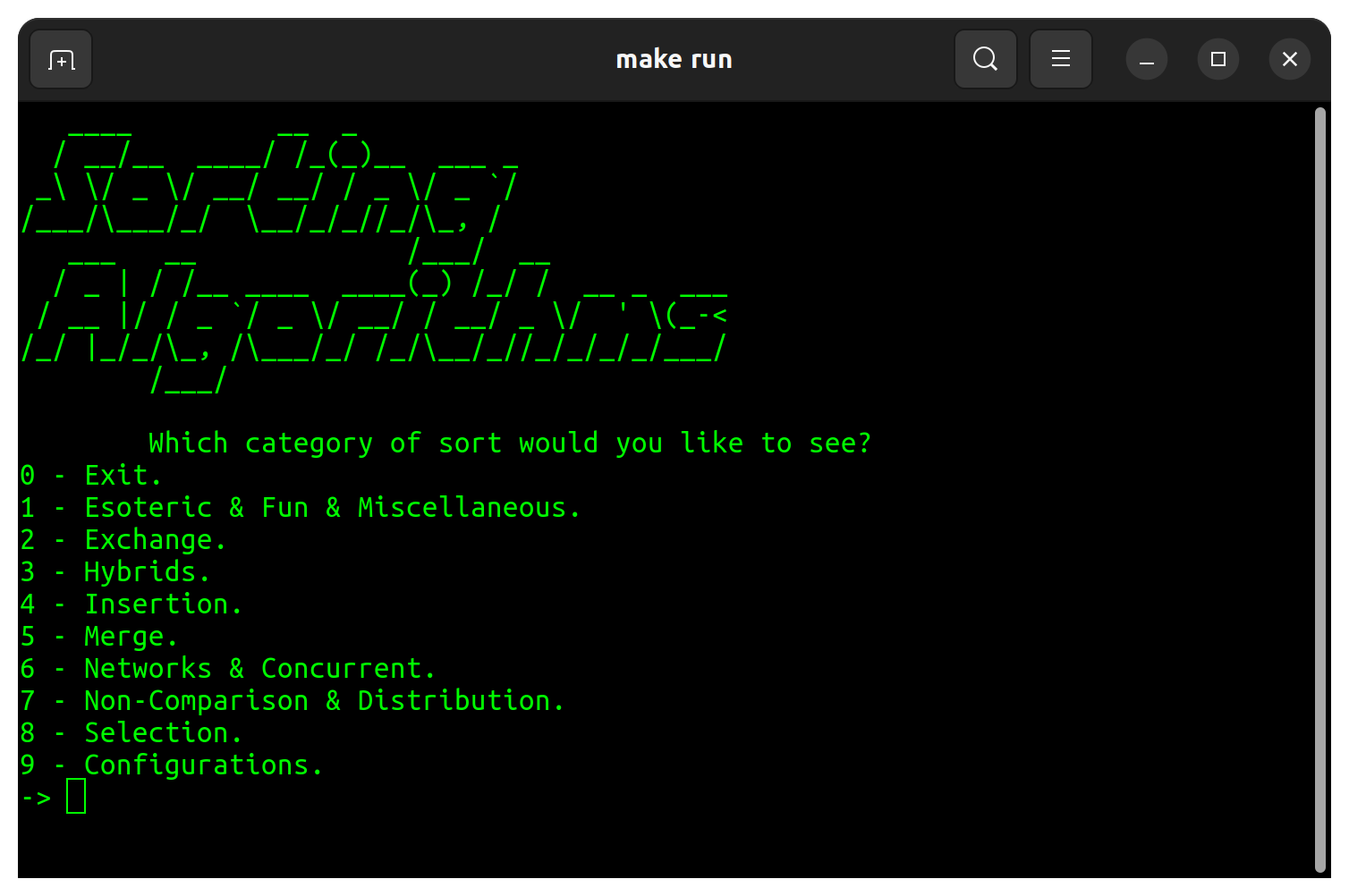
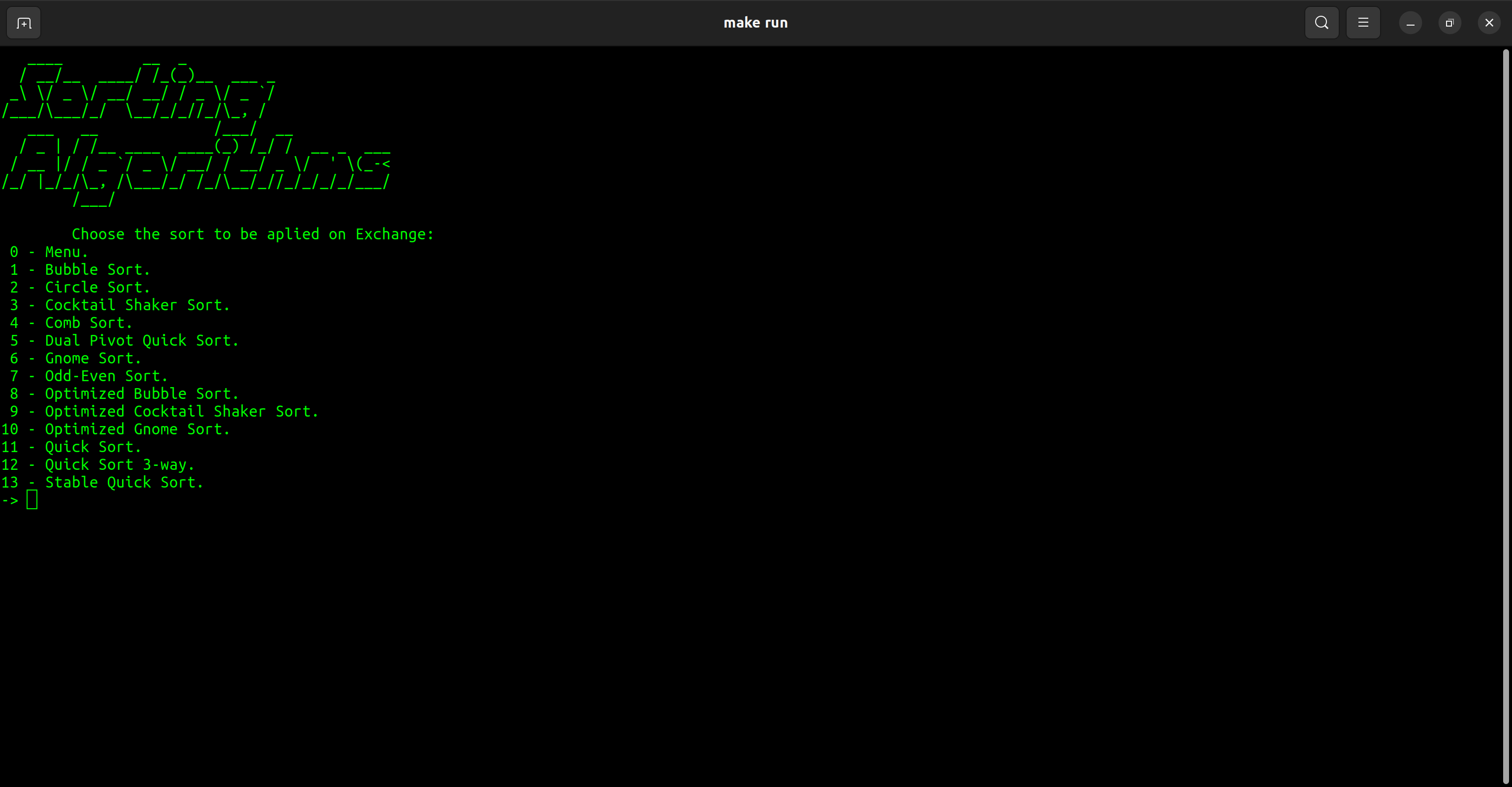
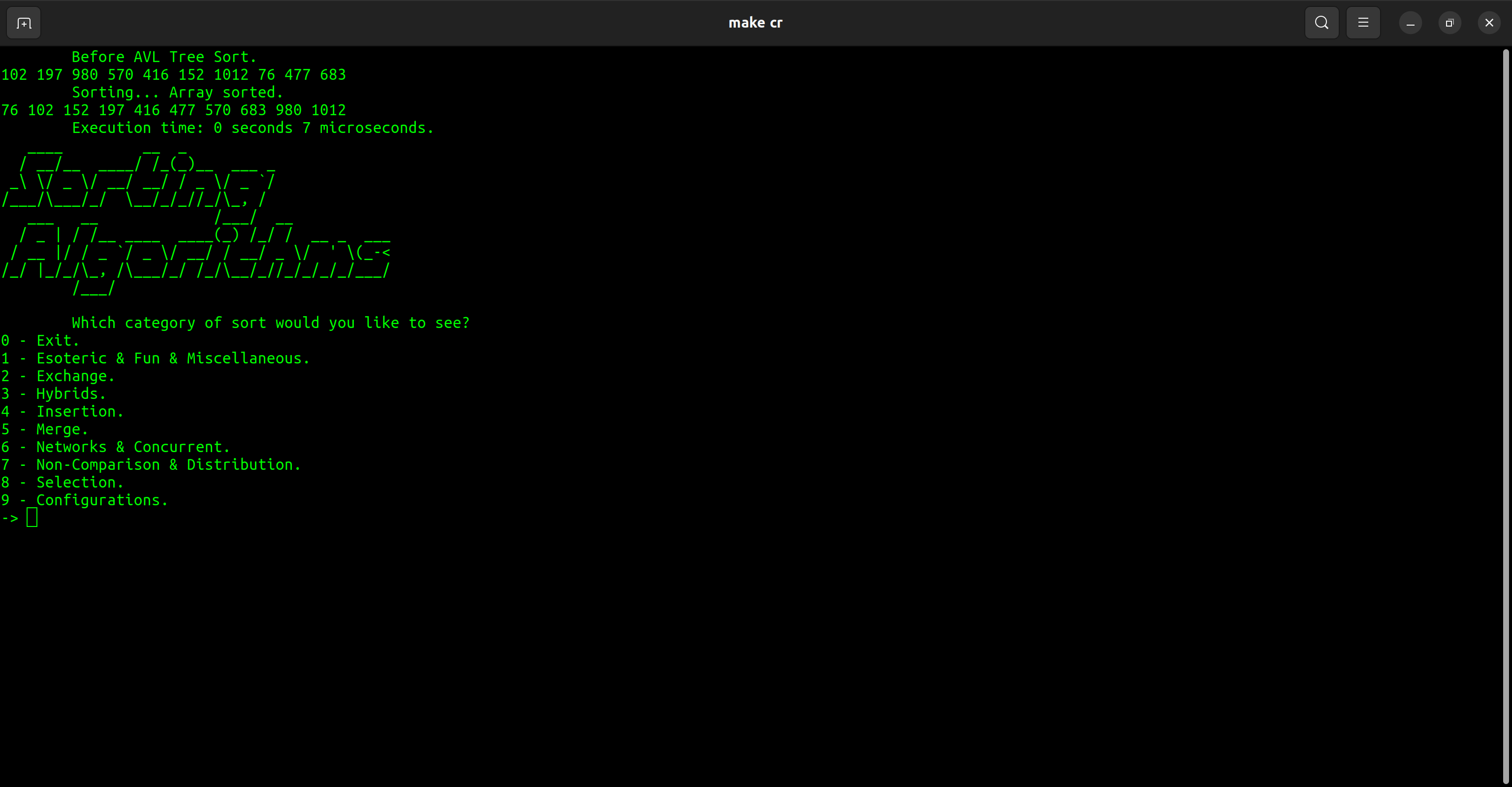
| カテゴリ | 選別 |
|---|---|
| 難解で楽しく&その他 | 悪いソート ボゴボゴソート ボゴソート バブルボゴソート カクテルボゴソート Bogoソートを交換します ボゴのソートが少ない パンケーキソート 愚かなソート スリープソート 遅いソート スパゲッティソート Stooge Sort |
| 交換 | バブルソート サークルソート カクテルシェーカーソート 櫛のソート デュアルピボットクイックソート gnomeソート 奇数 - されています 最適化されたバブルソート 最適化されたカクテルシェーカーソート 最適化されたGNOMEソート クイックソート クイックソート3ウェイ 安定したクイックソート |
| ハイブリッド | ティムソート |
| 挿入 | AVLツリーソート バイナリ挿入ソート サイクルソート 挿入ソート 忍耐のソート シェルソート ツリーソート |
| マージ | ボトムアップマージソート インプレースマージソート ソートをマージします |
| ネットワークと同時 | Bitonicソート ペアワイズネットワークソート |
| 非比較および分布 | バケットソート カウントソート 重力(ビーズ)ソート ピジョンホールソート RADIX LSDソート |
| 選択 | ダブル選択ソート 最大ヒープソート 最小ヒープソート 選択ソート |
| アルゴリズム | 最悪の場合 | ベストケース | 平均 | スペースの複雑さ | インプレース | 安定した | メモ |
|---|---|---|---|---|---|---|---|
| 悪いソート | O(n³) | O(n³) | O(n³) | o(1) | ✔✔️ | ||
| ボゴボゴソート | O(無限) | O(n²) | o((n+1)!) | o(1) | ✔✔️ | 最悪のケースは、ランダムな操作のために無制限になる可能性があります | |
| ボゴソート | O(無限) | の上) | o((n+1)!) | o(1) | ✔✔️ | 最悪のケースは、ランダムな操作のために無制限になる可能性があります | |
| バブルボゴソート | O(無限) | の上) | o((n+1)!) | o(1) | ✔✔️ | ✔✔️ | 最悪のケースは、ランダムな操作のために無制限になる可能性があります |
| カクテルボゴソート | O(無限) | の上) | o((n+1)!) | o(1) | ✔✔️ | 最悪のケースは、ランダムな操作のために無制限になる可能性があります | |
| Bogoソートを交換します | O(無限) | の上) | o((n+1)!) | o(1) | ✔✔️ | 最悪のケースは、ランダムな操作のために無制限になる可能性があります | |
| ボゴのソートが少ない | O(無限) | O(n²) | o((n+1)!) | o(1) | ✔✔️ | 最悪のケースは、ランダムな操作のために無制限になる可能性があります | |
| パンケーキソート | O(n²) | O(n²) | O(n²) | o(1) | ✔✔️ | ||
| 愚かなソート | O(n²) | O(n²) | O(n²) | o(1) | ✔✔️ | ||
| スリープソート | o(int_max) | o(max(input) + n) | o(max(input) + n) | の上) | ✔✔️ | CPUスケジューラを使用してソートします | |
| 遅いソート | o(n*n!) | の上) | o((n+1)!) | o(1) | ✔✔️ | ||
| スパゲッティソート | の上) | の上) | の上) | の上) | ✔✔️ | ||
| Stooge Sort |  |  |  | の上) | |||
| バブルソート | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| サークルソート | o(n log n log n) | o(n log n) | o(n log n) | o(1) | ✔✔️ | ||
| カクテルシェーカーソート | O(n²) | O(n²) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| 櫛のソート | O(n²) | o(n log n) | 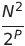 | o(1) | ✔✔️ | Pは増分数です | |
| デュアルピボットクイックソート | O(n²) | o(n log n) | o(n log n) | o(log n) | ✔✔️ | ||
| gnomeソート | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| 奇数 - されています | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| 最適化されたバブルソート | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| 最適化されたカクテルシェーカーソート | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| 最適化されたGNOMEソート | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| クイックソート | O(n²) | o(n log n) | o(n log n) | o(log n) | ✔✔️ | ||
| クイックソート3ウェイ | O(n²) | の上) | o(n log n) | o(log n)またはo(n) | ✔✔️ | ||
| 安定したクイックソート | O(n²) | o(n log n) | o(n log n) | の上) | ✔✔️ | ✔✔️ | |
| ティムソート | o(n log n) | の上) | o(n log n) | の上) | ✔✔️ | ||
| AVLツリーソート | o(n log n) | の上) | o(n log n) | の上) | ✔✔️ | 最悪の場合、バイナリ検索ツリーを使用する場合、o(n²)自己バランスのとれたバイナリ検索ツリーを使用する場合は、o(n log n) | |
| バイナリ挿入ソート | o(n log n) | の上) | o(n log n) | o(1) | ✔✔️ | ✔✔️ | |
| サイクルソート | O(n²) | O(n²) | O(n²) | o(1) | ✔✔️ | ||
| 挿入ソート | O(n²) | の上) | O(n²) | o(1) | ✔✔️ | ✔✔️ | |
| 忍耐のソート | o(n log n) | の上) | o(n log n) | の上) | ✔✔️ | ||
| シェルソート | 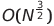 またはo(nlog²n) またはo(nlog²n) | o(n log n) | o(n^1.25)からo(n²)へ | o(1) | ✔✔️ | ||
| ツリーソート | O(n²) | o(n log n) | o(n log n) | の上) | ✔✔️ | 最悪の場合、バイナリ検索ツリーを使用する場合、o(n²)自己バランスのとれたバイナリ検索ツリーを使用する場合は、o(n log n) | |
| ボトムアップマージソート | o(n log n) | o(n log n) | o(n log n) | の上) | ✔✔️ | ||
| インプレースマージソート | O(n²) | O(n²) | O(n²) | o(log n) | ✔✔️ | ✔✔️ | |
| ソートをマージします | o(n log n) | o(n log n) | o(n log n) | の上) | ✔✔️ | ||
| Bitonicソート | o(log²n) | o(log²n) | o(log²n) | o(nlog²n) | ✔✔️ | ||
| ペアワイズネットワークソート | 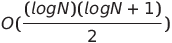 またはo(n log n) またはo(n log n) | o(n log n) | o(n log n) | 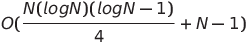 | ✔✔️ | 最悪の場合は、平行時間と空間の複雑さを使用することです。 | |
| バケットソート | O(n²) | o(n+k) | o(n+k) | o(n+k) | ✔✔️ | Kはバケットの数です | |
| カウントソート | o(n+k) | o(n+k) | o(n+k) | o(n+k) | ✔✔️ | Kは入力データの範囲です | |
| 重力(ビーズ)ソート | o(s) | o(1)または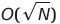 | の上) | O(n²) | ✔✔️ | sは配列要素の合計であり、o(1)は実際には実装できません | |
| ピジョンホールソート | o(n+n) | o(n+n) | o(n+n) | o(n+n) | ✔✔️ | nは要素の数、 nは入力データの範囲です | |
| RADIX LSDソート | O(NW) | O(NW) | O(NW) | の上) | ✔✔️ | wはmaxumum要素幅(ビット)です | |
| ダブル選択ソート | O(n²) | O(n²) | O(n²) | o(1) | ✔✔️ | 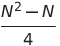 比較 比較 | |
| 最大ヒープソート | o(n log n) | o(n log n) | o(n log n) | o(1) | ✔✔️ | ||
| 最小ヒープソート | o(n log n) | o(n log n) | o(n log n) | o(1) | ✔✔️ | ||
| 選択ソート | O(n²) | O(n²) | O(n²) | o(1) | ✔✔️ | 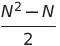 比較 比較 |