Sort_Algorithms
V1.1
Un programme pour afficher le temps d'exécution et la variation des algorithmes de tri dans le langage C Il existe 48 algorithmes de tri Avaliables distribués dans 8 catégories différentes.
Sur les paramètres du programme, il y a des modifications avalimes notées dans le tableau ci-dessous:
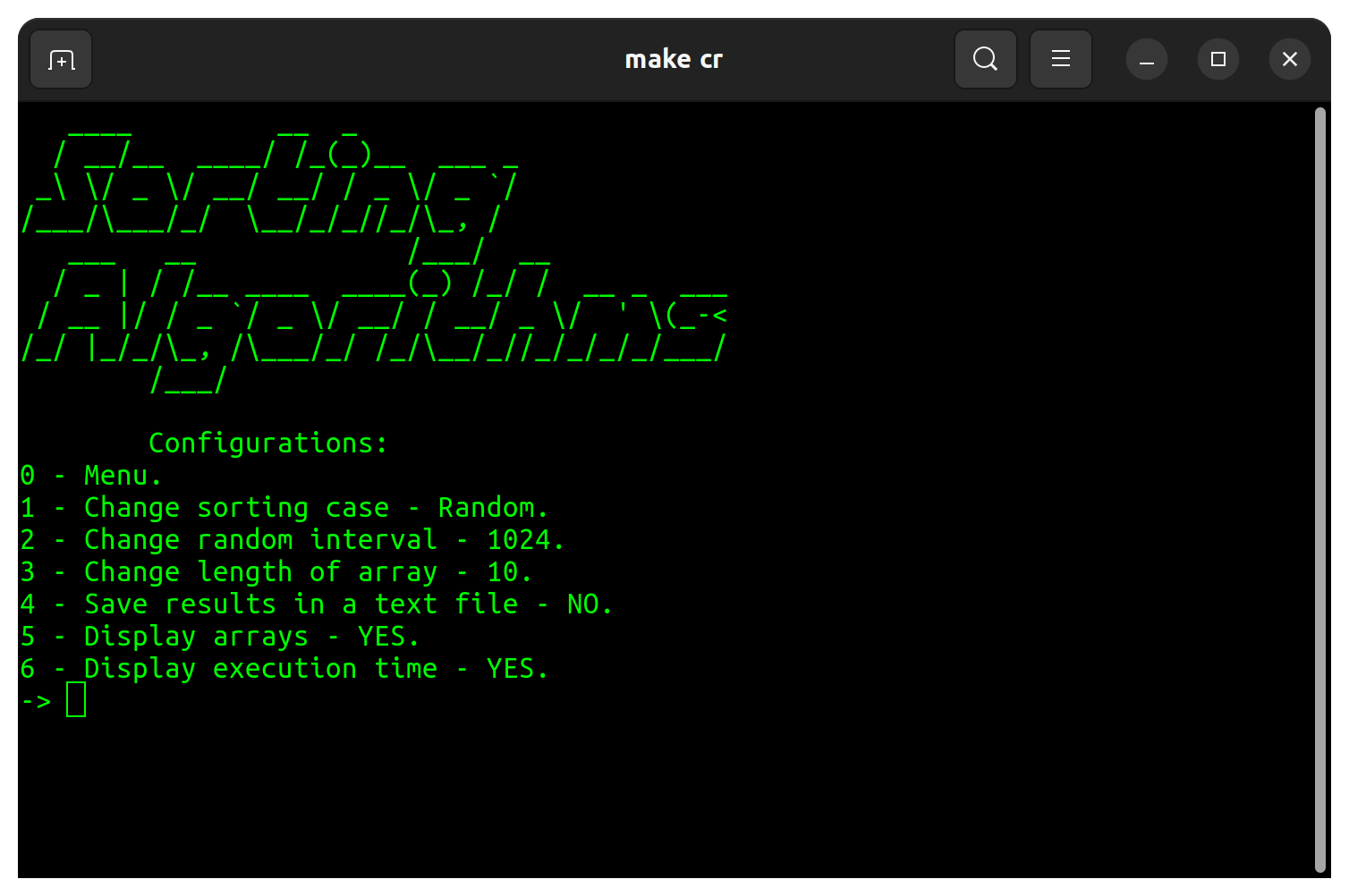
| Configuration | Défaut |
|---|---|
| Trieur | Aléatoire |
| Intervalle aléatoire | 32 |
| Durée du tableau | 10 |
| Enregistrer les résultats dans un fichier texte | NON |
| Afficher les tableaux | OUI |
| Afficher le temps d'exécution | OUI |
Remarque: vous devez faire installer le compilateur GCC dans votre machine pour exécuter les instructions ci-dessous pour exécuter le programme.
Ouvrez un terminal et allez dans le répertoire du projet. Exécuter make dans Terminal Permettez de compiler le programme. Commandes Avaliable pour exécuter avec Make ( make ${command} ):
| Commande | Description |
|---|---|
| faire le ménage | Effacer tous les objets générés |
| croisement | Compiler et courir |
| rmproper | Effacer tous les fichiers d'objets |
| courir | Exécuter le programme principal |
Sur l'invite de commande ou PowerShell et accédez au répertoire du projet et exécutez execute.bat .
| Catégorie | Trier |
|---|---|
| Ésotérique et amusant et divers | Mauvaise sorte Bogo bogo tri Tri bogo Bubble Bogo Toi Cocktail Bogo Sort ÉCHANGE DE BOGO Moins de bogo Tri de crêpes Tri idiot Sommeil Lent Toi de spaghetti Toi des lancers |
| Échange | Tri bulle Tricoter Toi de shaker à cocktails Peigne Tour rapide du double pivot Tri de gnome Toi étrange-même Tri à bulles optimisé Toi de shaker à cocktail optimisé Tour de gnome optimisé Tri rapide Sort rapide à 3 voies Sort rapide stable |
| Hybrides | Toi Tim |
| Insertion | Toi de l'arbre AVL Tri binaire Toi de cycle Tri insertion Toi de patience Tri Tri |
| Fusionner | Sort de fusion ascendant Tri de fusion en place Fusion |
| Réseaux et concurrents | Tri bitonic Tri de réseau par paire |
| Non-comparaison et distribution | Trier Tri de comptage Tri de gravité (perle) Pigeonhole Sort Radix LSD Toi |
| Sélection | Tri à double sélection Toi de tas max Toi de tas de min Tri de sélection |
| Algorithme | Pire | Meilleur cas | Moyenne | Complexité spatiale | En place | Écurie | Notes |
|---|---|---|---|---|---|---|---|
| Mauvaise sorte | O (n³) | O (n³) | O (n³) | O (1) | ✔️ | ||
| Bogo bogo tri | O (Infinity) | O (n²) | O ((n + 1)!) | O (1) | ✔️ | Le pire des cas peut être illimité en raison d'une manipulation aléatoire | |
| Tri bogo | O (Infinity) | SUR) | O ((n + 1)!) | O (1) | ✔️ | Le pire des cas peut être illimité en raison d'une manipulation aléatoire | |
| Bubble Bogo Toi | O (Infinity) | SUR) | O ((n + 1)!) | O (1) | ✔️ | ✔️ | Le pire des cas peut être illimité en raison d'une manipulation aléatoire |
| Cocktail Bogo Sort | O (Infinity) | SUR) | O ((n + 1)!) | O (1) | ✔️ | Le pire des cas peut être illimité en raison d'une manipulation aléatoire | |
| ÉCHANGE DE BOGO | O (Infinity) | SUR) | O ((n + 1)!) | O (1) | ✔️ | Le pire des cas peut être illimité en raison d'une manipulation aléatoire | |
| Moins de bogo | O (Infinity) | O (n²) | O ((n + 1)!) | O (1) | ✔️ | Le pire des cas peut être illimité en raison d'une manipulation aléatoire | |
| Tri de crêpes | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Tri idiot | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Sommeil | O (int_max) | O (max (entrée) + n) | O (max (entrée) + n) | SUR) | ✔️ | Utilisez le planificateur CPU pour trier | |
| Lent | O (n * n!) | SUR) | O ((n + 1)!) | O (1) | ✔️ | ||
| Toi de spaghetti | SUR) | SUR) | SUR) | SUR) | ✔️ | ||
| Toi des lancers |  |  |  | SUR) | |||
| Tri bulle | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Tricoter | O (n log n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Toi de shaker à cocktails | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ✔️ | |
| Peigne | O (n²) | O (n log n) | 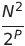 | O (1) | ✔️ | P est le nombre d'incréments | |
| Tour rapide du double pivot | O (n²) | O (n log n) | O (n log n) | O (log n) | ✔️ | ||
| Tri de gnome | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Toi étrange-même | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Tri à bulles optimisé | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Toi de shaker à cocktail optimisé | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Tour de gnome optimisé | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Tri rapide | O (n²) | O (n log n) | O (n log n) | O (log n) | ✔️ | ||
| Sort rapide à 3 voies | O (n²) | SUR) | O (n log n) | O (log n) ou o (n) | ✔️ | ||
| Sort rapide stable | O (n²) | O (n log n) | O (n log n) | SUR) | ✔️ | ✔️ | |
| Toi Tim | O (n log n) | SUR) | O (n log n) | SUR) | ✔️ | ||
| Toi de l'arbre AVL | O (n log n) | SUR) | O (n log n) | SUR) | ✔️ | Dans le pire des cas, O (n²) lors de l'utilisation de l'arbre de recherche binaire et O (n log n) lors de l'utilisation de l'arbre de recherche binaire auto-équilibré | |
| Tri binaire | O (n log n) | SUR) | O (n log n) | O (1) | ✔️ | ✔️ | |
| Toi de cycle | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | ||
| Tri insertion | O (n²) | SUR) | O (n²) | O (1) | ✔️ | ✔️ | |
| Toi de patience | O (n log n) | SUR) | O (n log n) | SUR) | ✔️ | ||
| Tri | 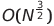 ou o (n log² n) ou o (n log² n) | O (n log n) | O (n ^ 1.25) à o (n²) | O (1) | ✔️ | ||
| Tri | O (n²) | O (n log n) | O (n log n) | SUR) | ✔️ | Dans le pire des cas, O (n²) lors de l'utilisation de l'arbre de recherche binaire et O (n log n) lors de l'utilisation de l'arbre de recherche binaire auto-équilibré | |
| Sort de fusion ascendant | O (n log n) | O (n log n) | O (n log n) | SUR) | ✔️ | ||
| Tri de fusion en place | O (n²) | O (n²) | O (n²) | O (log n) | ✔️ | ✔️ | |
| Fusion | O (n log n) | O (n log n) | O (n log n) | SUR) | ✔️ | ||
| Tri bitonic | O (log² n) | O (log² n) | O (log² n) | O (n log² n) | ✔️ | ||
| Tri de réseau par paire | 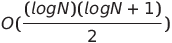 ou o (n log n) ou o (n log n) | O (n log n) | O (n log n) | 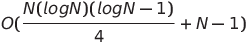 | ✔️ | Le pire des cas est d'utiliser le temps parallèle et la complexité spatiale non parallèle | |
| Trier | O (n²) | O (n + k) | O (n + k) | O (n + k) | ✔️ | k est le nombre de seaux | |
| Tri de comptage | O (n + k) | O (n + k) | O (n + k) | O (n + k) | ✔️ | k est la gamme de données d'entrée | |
| Tri de gravité (perle) | O (s) | O (1) ou 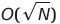 | SUR) | O (n²) | ✔️ | S est la somme des éléments du tableau, O (1) ne peut pas être mis en œuvre dans la pratique | |
| Pigeonhole Sort | O (n + n) | O (n + n) | O (n + n) | O (n + n) | ✔️ | N est le nombre d'éléments et n est la plage de données d'entrée | |
| Radix LSD Toi | O (NW) | O (NW) | O (NW) | SUR) | ✔️ | W est la largeur des éléments maxumums (bits) | |
| Tri à double sélection | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | 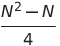 Comparaisons Comparaisons | |
| Toi de tas max | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Toi de tas de min | O (n log n) | O (n log n) | O (n log n) | O (1) | ✔️ | ||
| Tri de sélection | O (n²) | O (n²) | O (n²) | O (1) | ✔️ | 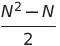 Comparaisons Comparaisons |