การใช้งาน Pytorch สำหรับวิธีการอนุมานโดยประมาณดังต่อไปนี้:
เรายังให้รหัสสำหรับ:
โครงการเขียนด้วย Python 2.7 และ Pytorch 1.0.1 หาก Cuda พร้อมใช้งานจะถูกใช้โดยอัตโนมัติ แบบจำลองยังสามารถทำงานบน CPU เนื่องจากไม่ใหญ่เกินไป
เราดำเนินการสัมผัสการถดถอยแบบ homoscedastic และ heteroscedastic ในชุดข้อมูลของเล่นที่สร้างขึ้นด้วย (ความจริงภาคพื้นดินของกระบวนการเกาส์เซียน) เช่นเดียวกับข้อมูลจริง (ชุดข้อมูล UCI หกชุด)
โน๊ตบุ๊ค/การจำแนก/(ModelName) _ (ExperimentType) .iPynb : มีการทดลองโดยใช้ (ModelName) บน (ExperimentType), เช่น homoscedastic/heteroscedastic สมุดบันทึก heteroscedastic มีทั้งการทดลองชุดข้อมูลของเล่นและ UCI สำหรับ (ModelName) ที่กำหนด
นอกจากนี้เรายังมีสมุดบันทึก Google Colab ซึ่งหมายความว่าคุณสามารถทำงานบน GPU (ฟรี!) ไม่จำเป็นต้องมีการแก้ไข -การพึ่งพาและชุดข้อมูลทั้งหมดจะถูกเพิ่มจากภายในโน้ตบุ๊ก -ยกเว้นการเลือกรันไทม์ -> เปลี่ยนประเภทรันไทม์ -> ฮาร์ดแวร์เร่งความเร็ว -> GPU
Train_ (ModelName) _ (ชุดข้อมูล) .py : รถไฟ (ModelName) บน (ชุดข้อมูล) ตัวชี้วัดการฝึกอบรมและน้ำหนักแบบจำลองจะถูกบันทึกลงในไดเรกทอรีที่ระบุ
SRC/ : ยูทิลิตี้ทั่วไปและคำจำกัดความรุ่น
สมุดบันทึก/การจำแนกประเภท : โน๊ตบุ๊คที่อนุญาตให้มีการฝึกอบรมแบบจำลองการประเมินและการทำงานของการทดลองความไม่แน่นอนของการหมุนหลัก พวกเขายังอนุญาตให้มีการวางแผนการกระจายน้ำหนักและการตัดแต่งน้ำหนัก พวกเขาอนุญาตให้โหลดโมเดลที่ผ่านการฝึกอบรมมาก่อนสำหรับการทดลอง
(https://arxiv.org/abs/1505.05424)
โน๊ตบุ๊ค colab ที่มีแบบจำลองการถดถอย: BBP homoscedastic / heteroscedastic
ฝึกอบรมแบบจำลองเกี่ยวกับ MNIST:
python train_BayesByBackprop_MNIST.py [--model [MODEL]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]สำหรับคำอธิบายของข้อโต้แย้งของสคริปต์:
python train_BayesByBackprop_MNIST.py -hผลลัพธ์ที่ดีที่สุดจะได้รับก่อนหน้านี้
(https://arxiv.org/abs/1506.02557)
Bayes โดยการอนุมาน backprop ที่ค่าเฉลี่ยและความแปรปรวนของการเปิดใช้งานคำนวณในรูปแบบปิด การเปิดใช้งานจะถูกสุ่มตัวอย่างแทนน้ำหนัก สิ่งนี้ทำให้ความแปรปรวนของมาตราส่วนตัวประมาณ Monte Carlo Elbo เป็น 1/m โดยที่ M คือขนาด minibatch การสุ่มตัวอย่างน้ำหนักเครื่องชั่ง (M-1)/m ความแตกต่างของ KL ระหว่าง Gaussians สามารถคำนวณได้ในรูปแบบปิดลดความแปรปรวนเพิ่มเติม การคำนวณของแต่ละยุคนั้นเร็วกว่าและเป็นการบรรจบกัน
ฝึกอบรมแบบจำลองเกี่ยวกับ MNIST:
python train_BayesByBackprop_MNIST.py --model Local_Reparam [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]](https://arxiv.org/abs/1506.02142)
มีการตั้งค่าอัตราการออกกลางคันคงที่ 0.5
โน๊ตบุ๊ค colab ที่มีรูปแบบการถดถอย: MC Dropout homoscedastic heteroscedastic
ฝึกอบรมแบบจำลองเกี่ยวกับ MNIST:
python train_MCDropout_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]สำหรับคำอธิบายของข้อโต้แย้งของสคริปต์:
python train_MCDropout_MNIST.py -h(https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf)
เพื่อที่จะมาบรรจบกันกับหลังที่แท้จริงมากกว่า W อัตราการเรียนรู้ควรได้รับการอบอ่อนตามเงื่อนไขของ Robbins-Monro ในทางปฏิบัติเราใช้อัตราการเรียนรู้ที่แน่นอน
โน๊ตบุ๊ค colab ที่มีแบบจำลองการถดถอย: SGLD homoscedastic / heteroscedastic
ฝึกอบรมแบบจำลองเกี่ยวกับ MNIST:
python train_SGLD_MNIST.py [--use_preconditioning [USE_PRECONDITIONING]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]สำหรับคำอธิบายของข้อโต้แย้งของสคริปต์:
python train_SGLD_MNIST.py -h(https://arxiv.org/abs/1512.07666)
SGLD กับ RMSPROP preconditioning ควรใช้อัตราการเรียนรู้ที่สูงขึ้นกว่าวานิลลา SGLD
ฝึกอบรมแบบจำลองเกี่ยวกับ MNIST:
python train_SGLD_MNIST.py --use_preconditioning True [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]หลายเครือข่ายได้รับการฝึกฝนเกี่ยวกับชุดย่อยของชุดข้อมูล
โน๊ตบุ๊ค colab ที่มีแบบจำลองการถดถอย: แผนที่ชุด homoscedastic / heteroscedastic
ฝึกอบรมวงดนตรีเกี่ยวกับ MNIST:
python train_Bootrap_Ensemble_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--subsample [SUBSAMPLE]] [--n_nets [N_NETS]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]สำหรับคำอธิบายของข้อโต้แย้งของสคริปต์:
python train_Bootrap_Ensemble_MNIST.py -h(https://openreview.net/pdf?id=skdvd2xaz)
ฝึกอบรมเครือข่ายแผนที่จากนั้นคำนวณลำดับที่สองของ Taylor Series aproxiamtion ไปยังความโค้งรอบ ๆ โหมดของหลัง มีการใช้การประมาณ Hessian ในแนวทแยงซึ่งมีเพียงการพึ่งพาภายในชั้นเท่านั้น Hessian ได้รับการประมาณเพิ่มเติมเป็นผลิตภัณฑ์ Kronecker ของความคาดหวังของปัจจัย Hessian ของ Datapoint เดียว การประมาณ Hessian อาจใช้เวลาสักครู่ โชคดีที่ต้องทำเพียงครั้งเดียว
ฝึกอบรมเครือข่ายแผนที่บน MNIST และ Hessian โดยประมาณ:
python train_KFLaplace_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--hessian_diag_sig [HESSIAN_DIAG_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]สำหรับคำอธิบายของข้อโต้แย้งของสคริปต์:
python train_KFLaplace_MNIST.py -hโปรดทราบว่าเราบันทึกปัจจัยเฮสเซียนที่ไม่ได้รับการลดระดับและไม่ตรงกัน สิ่งนี้จะช่วยให้การเปลี่ยนแปลงราคาถูกในการคำนวณก่อนเวลาอนุมานก่อนเนื่องจาก Hessian ไม่จำเป็นต้องคำนวณใหม่ การอนุมานจะต้องมีการพลิกคว่ำปัจจัย Hessian และการสุ่มตัวอย่างจากการแจกแจงแบบปกติของเมทริกซ์ สิ่งนี้แสดงในโน้ตบุ๊ก/kfac_laplace_mnist.ipynb
(https://arxiv.org/abs/1402.4102)
เราใช้อัลกอริทึมรุ่นที่ปรับขนาดได้ซึ่งเสนอที่นี่เพื่อค้นหาพารามิเตอร์ไฮเปอร์พารามิเตอร์โดยอัตโนมัติในระหว่างการเผาไหม้ เราวาง Gaussian ก่อนหน้านี้บนน้ำหนักเครือข่ายและ Gamma Hyperprior เหนือความแม่นยำของ Gaussian
เรียกใช้ SG-HMC-SA Burn In และ Sampler ประหยัดน้ำหนักในไฟล์ที่ระบุ
python train_SGHMC_MNIST.py [--epochs [EPOCHS]] [--sample_freq [SAMPLE_FREQ]] [--burn_in [BURN_IN]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]สำหรับคำอธิบายของข้อโต้แย้งของสคริปต์:
python train_SGHMC_MNIST.py -hการอนุมานแผนที่ให้ค่าประมาณจุดของค่าพารามิเตอร์ เมื่อได้รับอินพุตจากการกระจายเช่นตัวเลขหมุนรุ่นเหล่านี้จะทำการคาดการณ์ที่ผิดด้วยความมั่นใจสูง
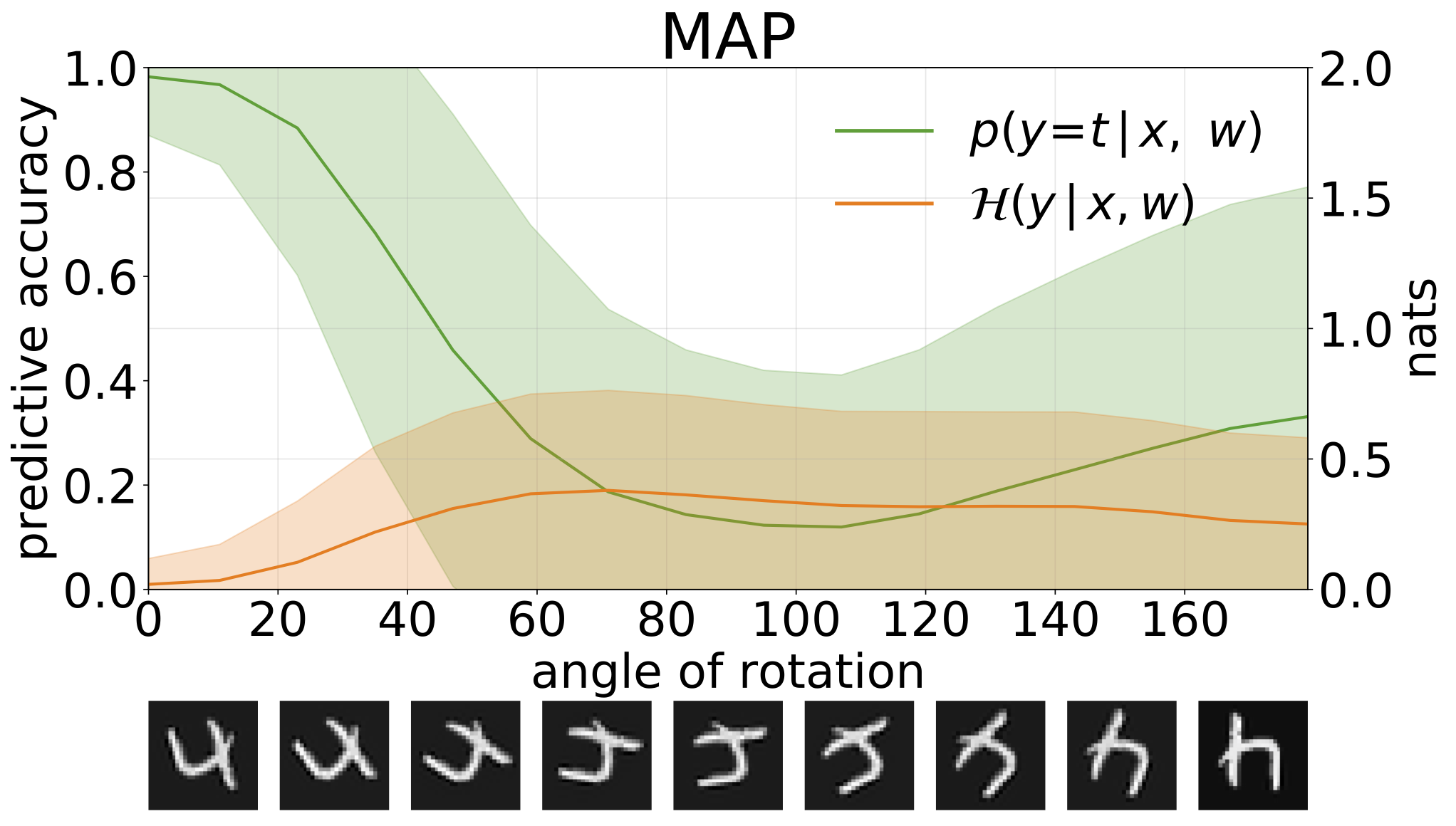
เราสามารถวัดความไม่แน่นอนในการทำนายแบบจำลองของเราผ่านเอนโทรปีที่ทำนายได้ เราสามารถย่อยสลายคำนี้เพื่อแยกแยะความไม่แน่นอนระหว่าง 2 ประเภท ความไม่แน่นอนที่เกิดจากเสียงรบกวนในข้อมูลหรือ ความไม่แน่นอนของ aleatoric สามารถหาปริมาณได้เป็นเอนโทรปีที่คาดหวังของการทำนายแบบจำลอง ความไม่แน่นอนของแบบจำลองหรือ ความไม่แน่นอนของ epistemic สามารถวัดได้ว่าเป็นความแตกต่างระหว่างเอนโทรปีทั้งหมดและเอนโทรปีของ Aleatoric
ภารกิจการถดถอยของเล่น homoscedastic ข้อมูลถูกสร้างขึ้นโดย GP ที่มีเคอร์เนล RBF (l = 1, σn = 0.3) เราใช้เครือข่าย FC เอาท์พุทเดียวที่มีชั้นที่ซ่อนอยู่หนึ่งชั้นของ 200 หน่วย relu เพื่อทำนายค่าเฉลี่ยการถดถอยμ (x) บันทึกที่คงที่σเรียนรู้แยกต่างหาก
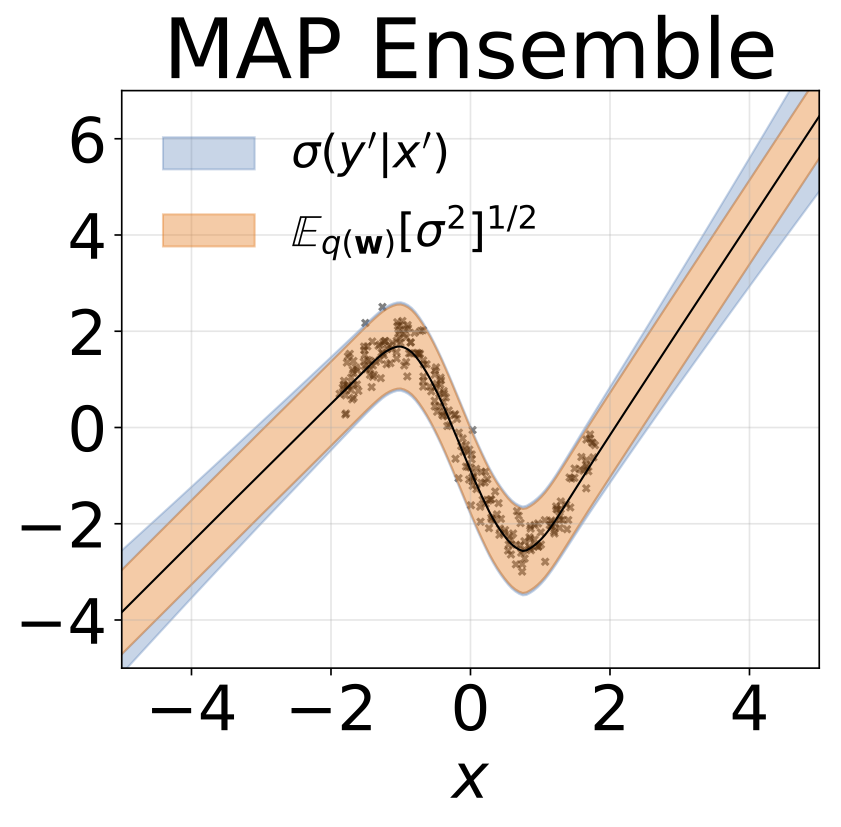
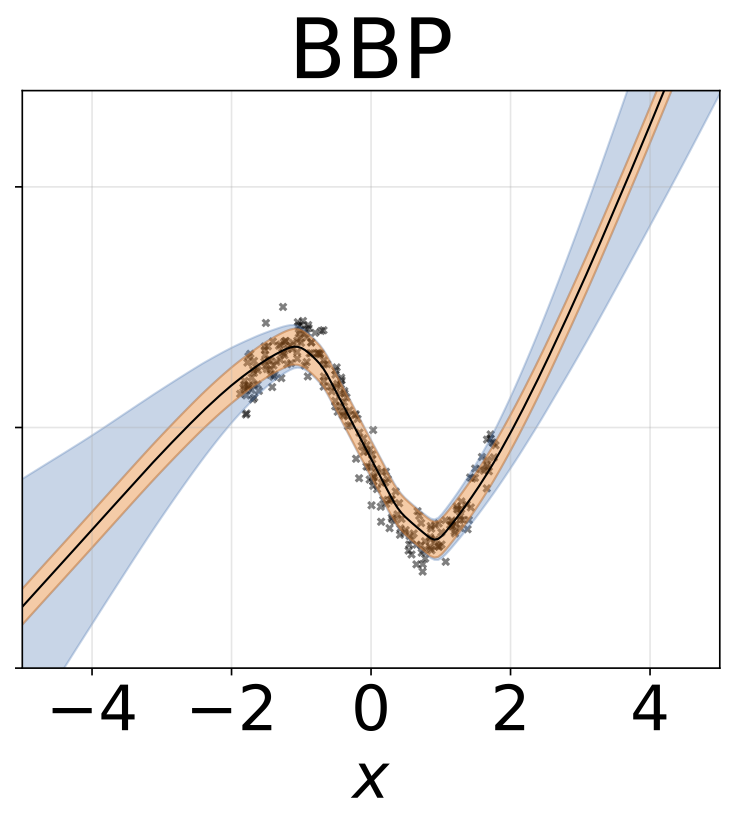
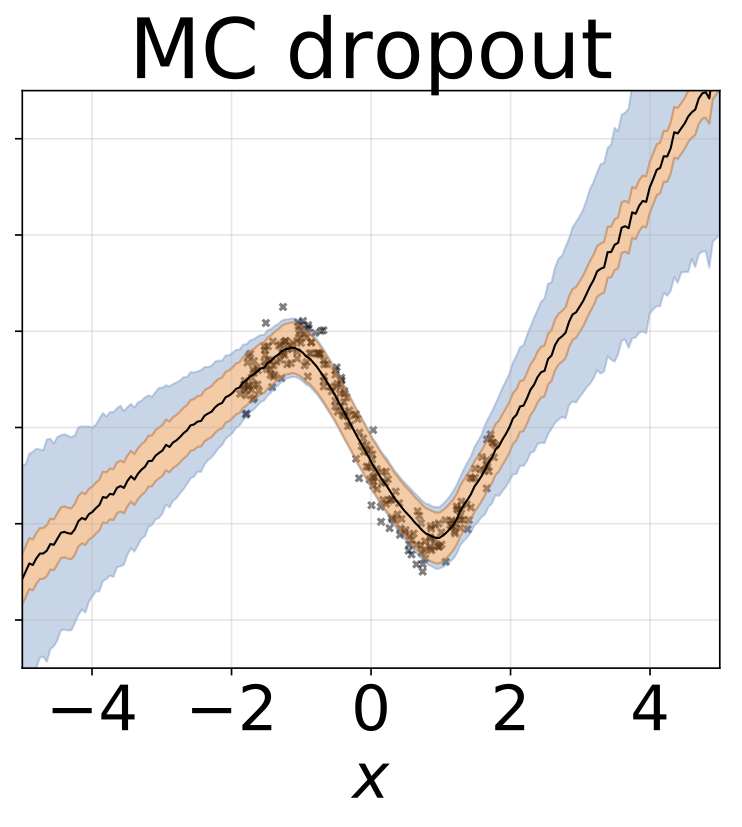
สถานการณ์เดียวกันกับส่วนก่อนหน้า แต่บันทึกσ (x) ถูกทำนายจากอินพุต
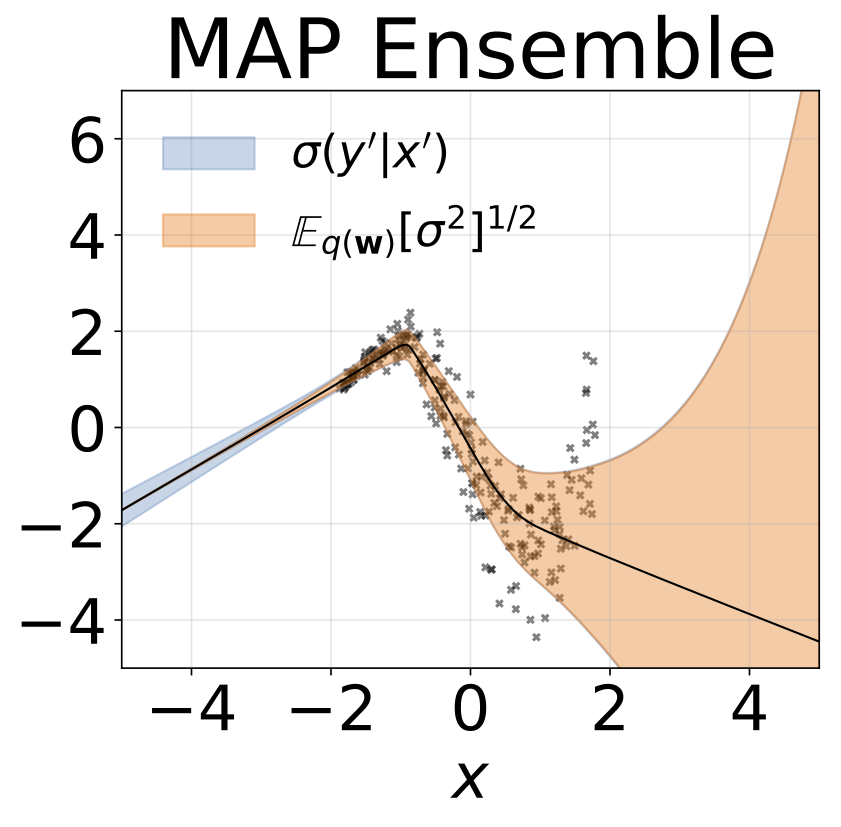
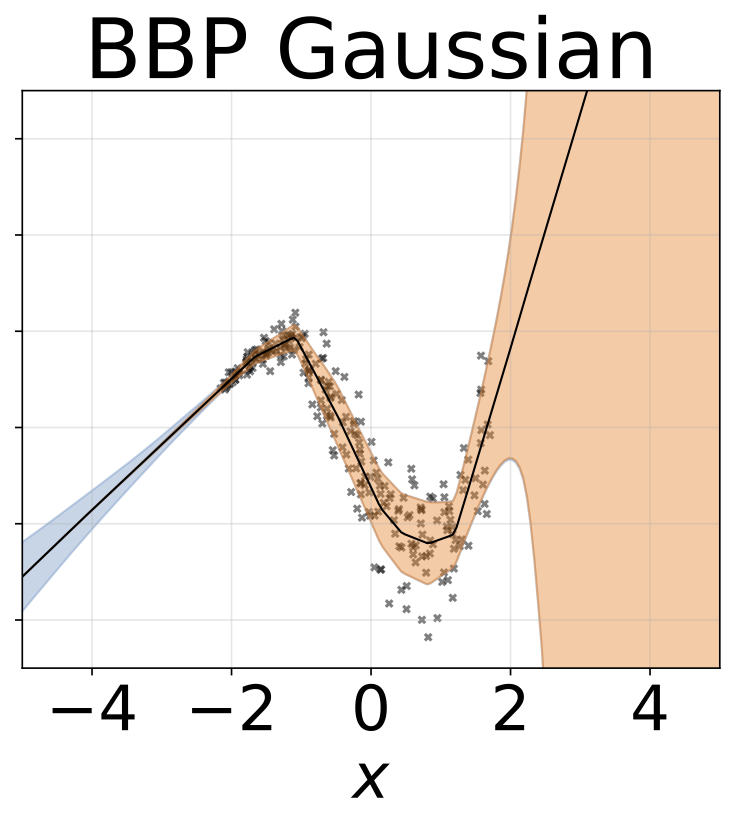
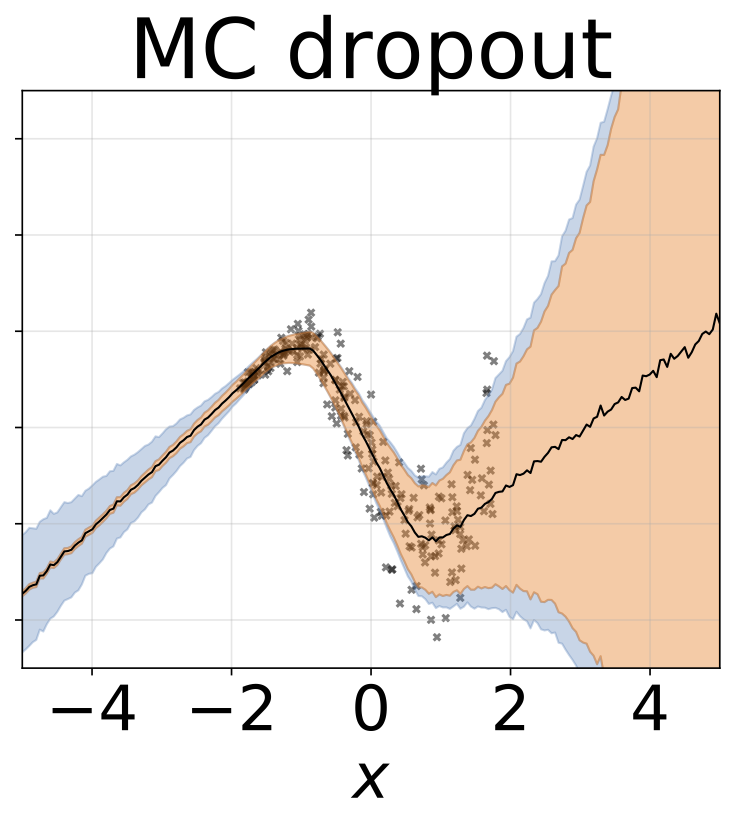
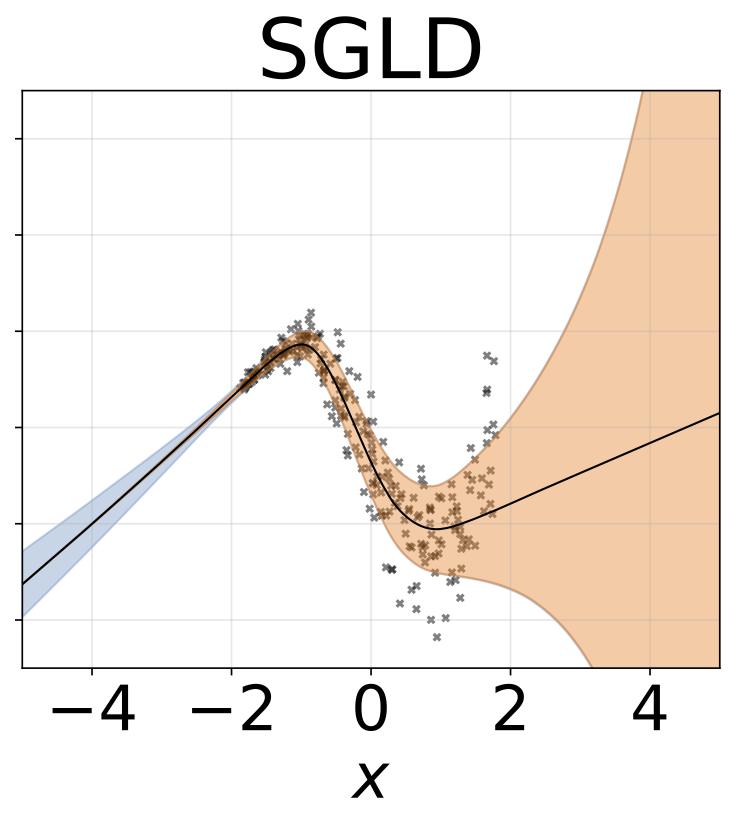
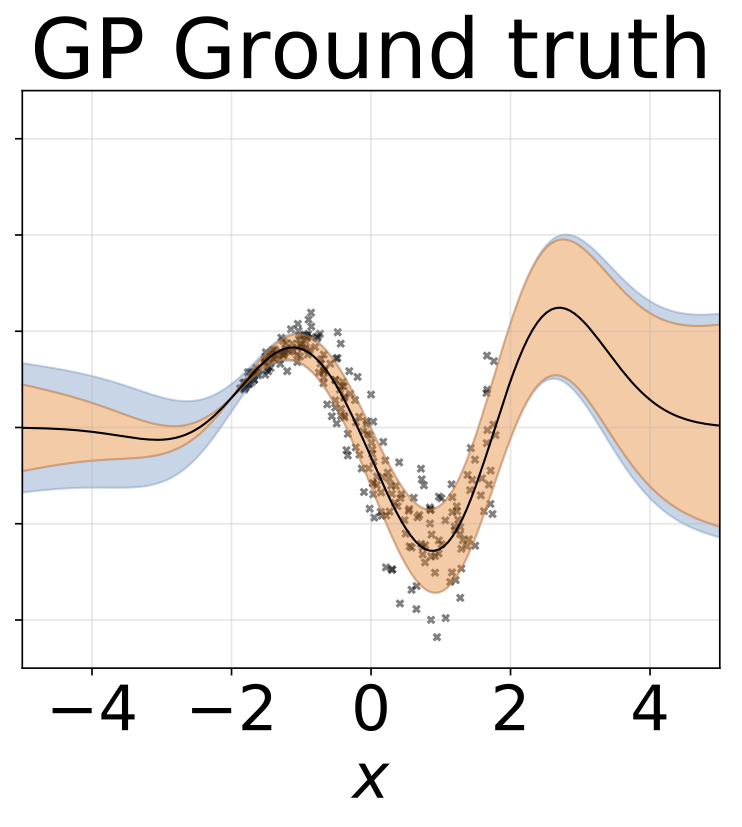
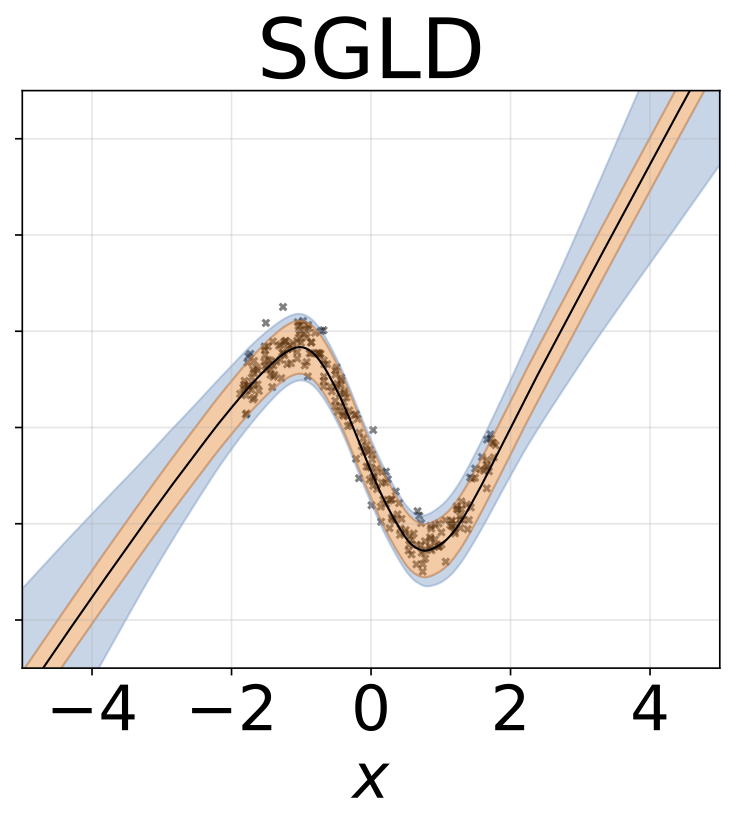
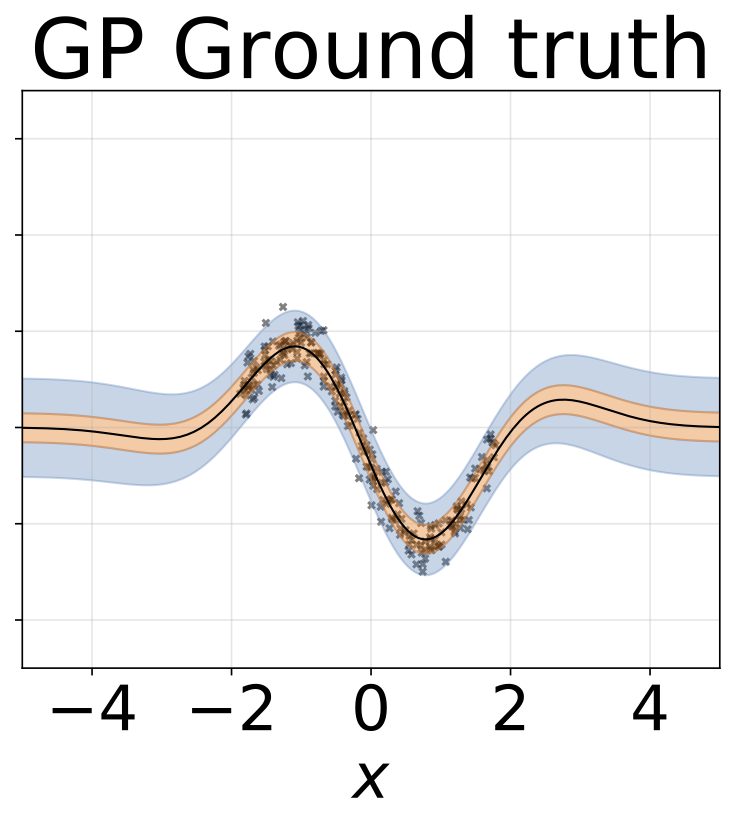
งานการถดถอยของเล่น heteroscedastic ข้อมูลถูกสร้างขึ้นโดย GP ที่มีเคอร์เนล RBF (l = 1 σn = 0.3 · | x + 2 |) เราใช้เครือข่ายสองหัวที่มี 200 หน่วย relu เพื่อทำนายค่าเฉลี่ยการถดถอยμ (x) และบันทึกการเบี่ยงเบนมาตรฐานมาตรฐานσ (x)
เราทำการถดถอยแบบ heteroscedastic ในชุดข้อมูล UCI หกชุด (ที่อยู่อาศัยคอนกรีตประสิทธิภาพการใช้พลังงานโรงไฟฟ้าไวน์แดงและชุดข้อมูลเรือยอชท์) โดยใช้การตรวจสอบความถูกต้องข้าม 10-Foild การทดลองทั้งหมดเหล่านี้มีอยู่ในสมุดบันทึก heteroscedastic โปรดทราบว่าผลลัพธ์ขึ้นอยู่กับการเลือกพารามิเตอร์ไฮเปอร์พารามิเตอร์เป็นอย่างมาก พล็อตด้านล่างแสดงโอกาสในการบันทึกและ RMSEs บนรถไฟ (สีกึ่งโปร่งใส) และการทดสอบ (สีทึบ) วงกลมและแถบข้อผิดพลาดสอดคล้องกับค่าเฉลี่ยการตรวจสอบข้าม 10 เท่าและค่าเบี่ยงเบนมาตรฐานตามลำดับ
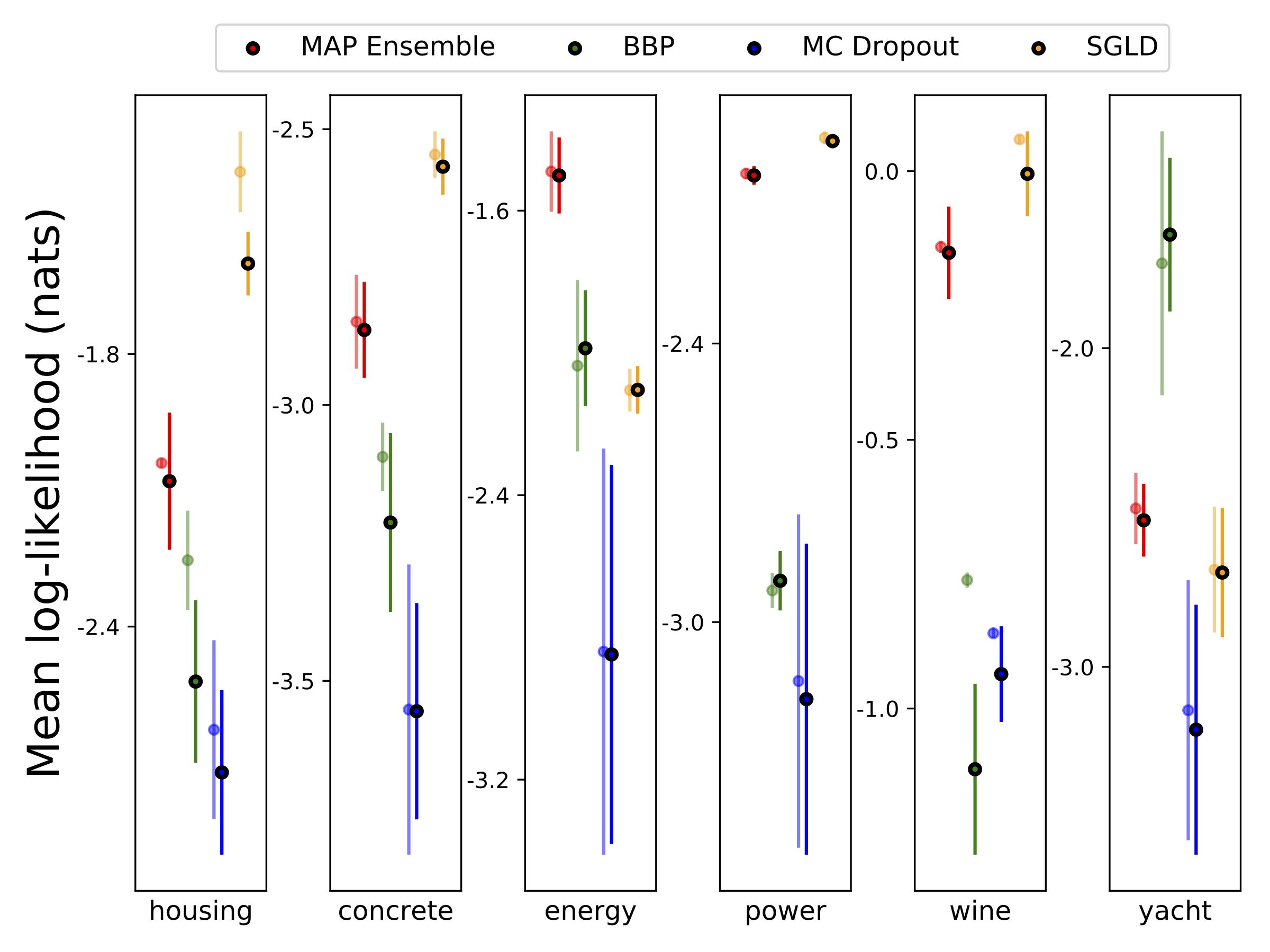
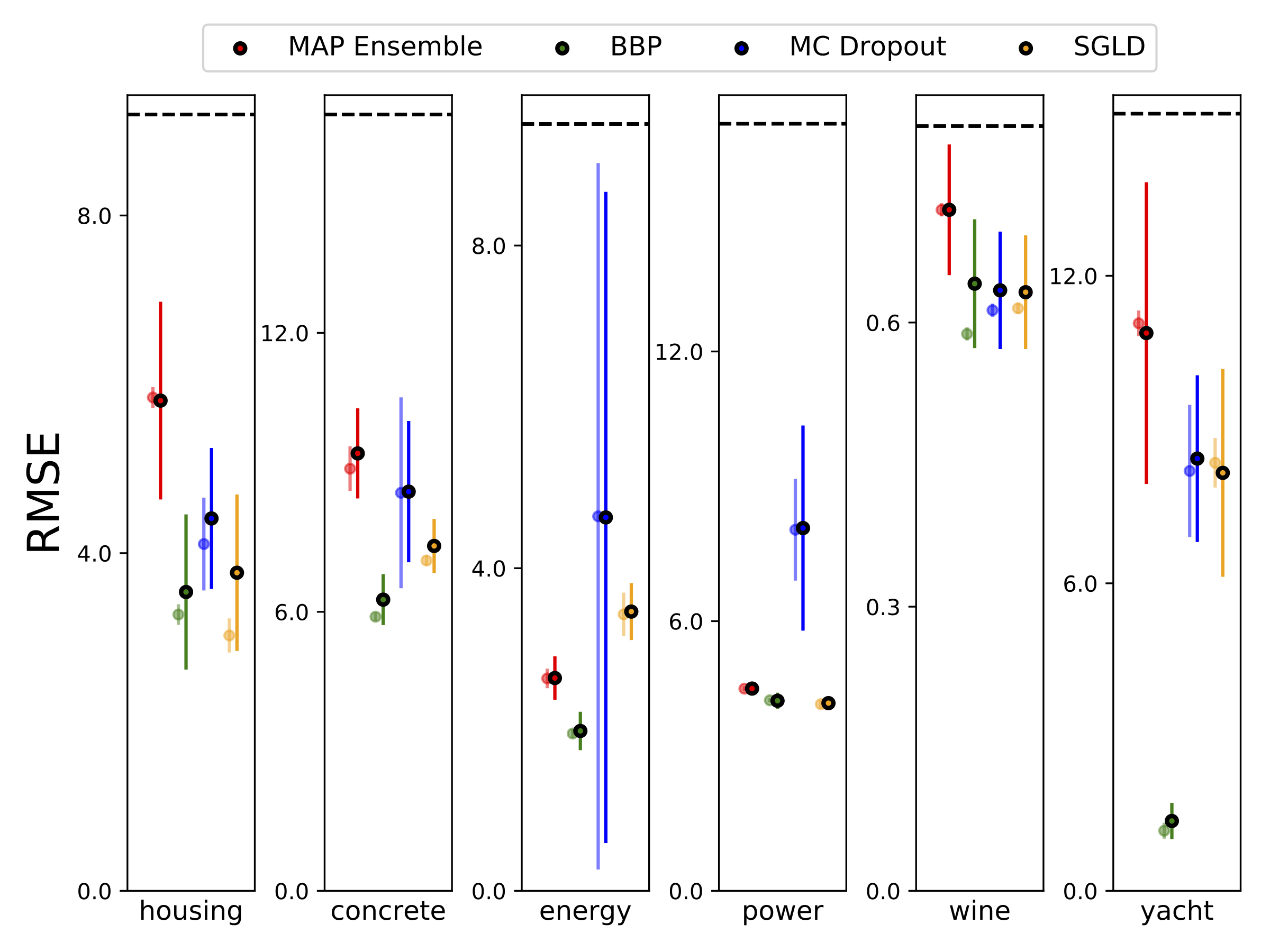
W ถูกทำให้เป็นชายขอบด้วยน้ำหนัก 100 ตัวอย่างสำหรับทุกรุ่นยกเว้น MAP โดยใช้น้ำหนักเพียงชุดเดียว
| การทดสอบ MNIST | แผนที่ | MAP Ensemble | BBP Gaussian | BBP GMM | bbp laplace | bbp reparam ท้องถิ่น | MC Dropout | SGLD | PSGLD |
|---|---|---|---|---|---|---|---|---|---|
| บันทึกเช่น | -572.9 | -496.54 | -1100.29 | -1008.28 | -892.85 | -1086.43 | -435.458 | -828.29 | -661.25 |
| ข้อผิดพลาด % | 1.58 | 1.53 | 2.60 | 2.38 | 2.28 | 2.61 | 1.37 | 1.76 | 1.76 |
ผลการทดสอบ MNIST สำหรับวิธีการที่อยู่ระหว่างการพิจารณา ยังไม่ได้ทำการปรับแต่งพารามิเตอร์ hyperparameter เราประมาณการกระจายการทำนายหลังด้วยตัวอย่าง 100 MC เราใช้เครือข่าย FC ที่มีเลเยอร์ Relu 1200 สองตัว หากไม่ระบุรายละเอียดก่อนหน้านี้คือ Gaussian กับ STD = 0.1 P-SGLD ใช้ RMSPROP preconditioning
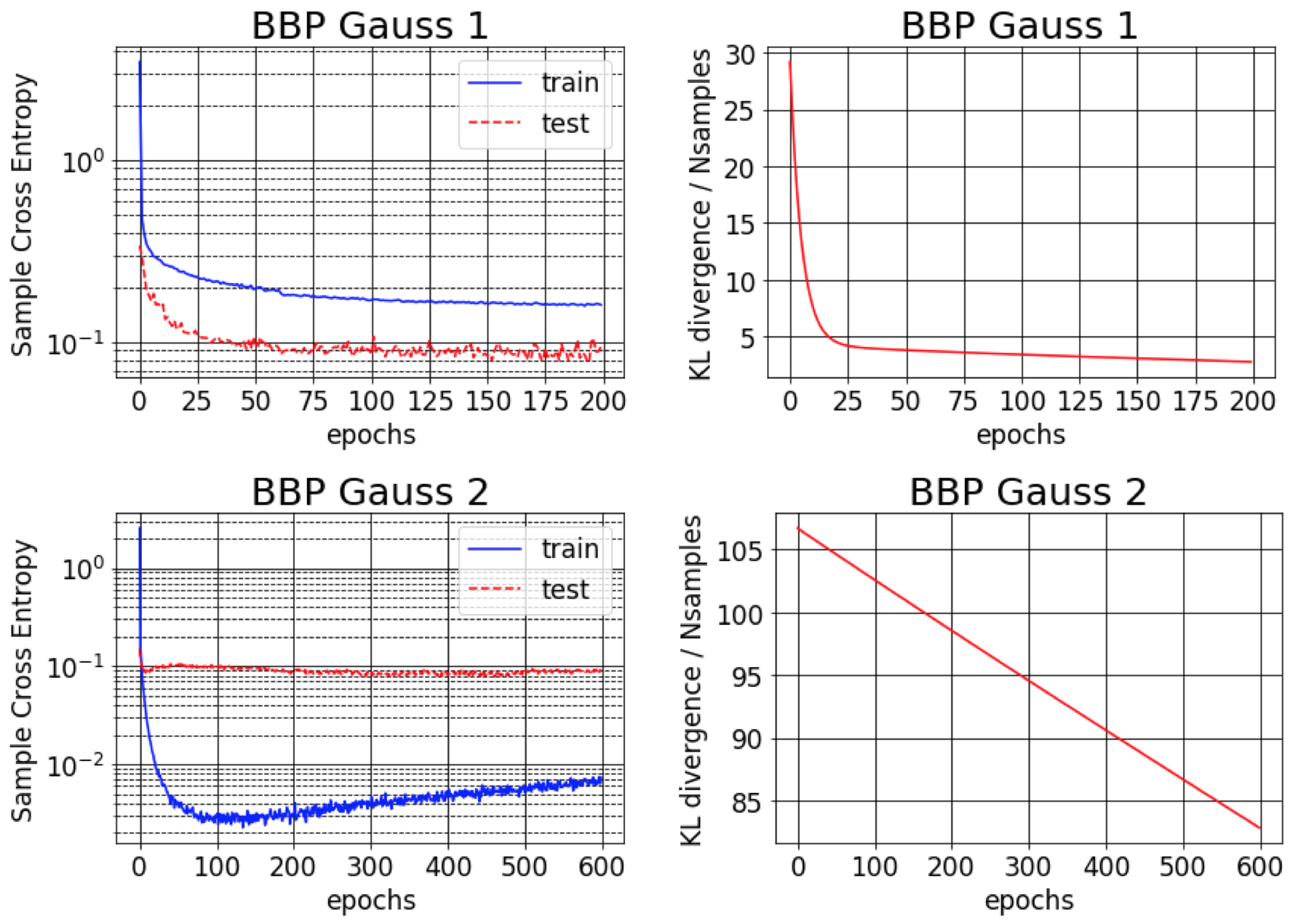
กระดาษต้นฉบับสำหรับ Bayes โดย Backprop รายงานข้อผิดพลาดประมาณ 1% สำหรับ MNIST เราพบว่าผลลัพธ์นี้สามารถบรรลุได้เฉพาะในกรณีที่ความแปรปรวนหลังโดยประมาณเริ่มต้นว่ามีขนาดเล็กมาก (BBP Gauss 2) ในสถานการณ์นี้การแจกแจงน้ำหนักมีลักษณะคล้ายกับเดลต้าให้ประสิทธิภาพการทำนายที่ดี แต่ประมาณความไม่แน่นอนที่ไม่ดี อย่างไรก็ตามเมื่อเริ่มต้นความแปรปรวนเพื่อให้ตรงกับก่อนหน้า (BBP Gauss 1) เราจะได้ผลลัพธ์ข้างต้น เส้นโค้งการฝึกอบรมสำหรับทั้งสองรูปแบบการกำหนดค่าไฮเปอร์พารามิเตอร์เหล่านี้แสดงอยู่ด้านล่าง:
ความไม่แน่นอนทั้งหมด, aleatoric และ epistemic ที่ได้รับเมื่อสร้างตัวอย่าง OOD โดยการเพิ่มชุดทดสอบ MNIST ด้วยการหมุน:
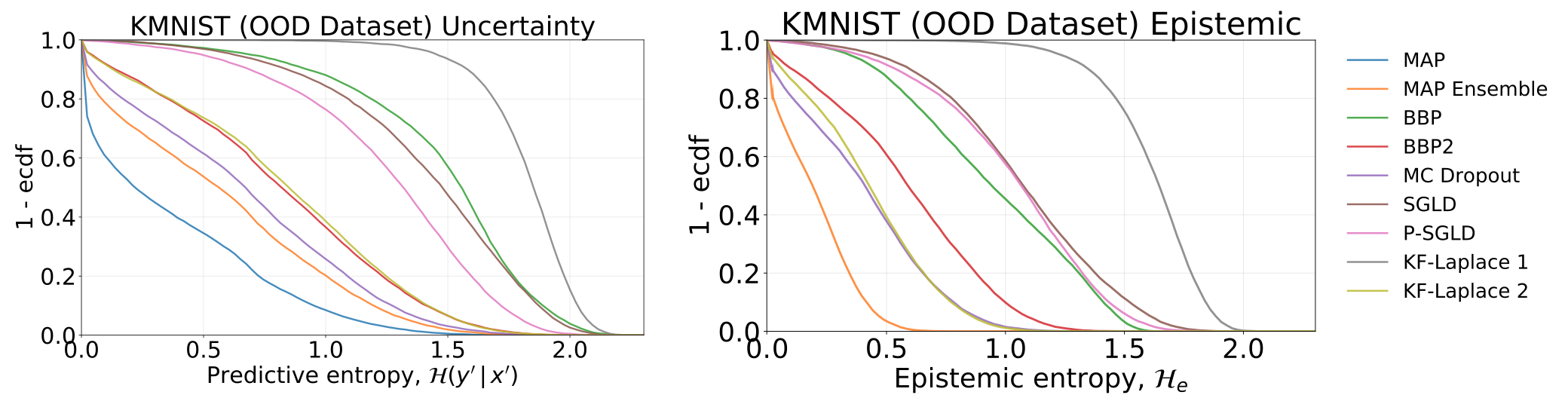
ความไม่แน่นอนทั้งหมดและ epistemic ที่ได้รับจากการทดสอบแบบจำลองของเรา - ซึ่งได้รับการฝึกอบรมเกี่ยวกับ MNIST - บนชุดข้อมูล KMNIST:
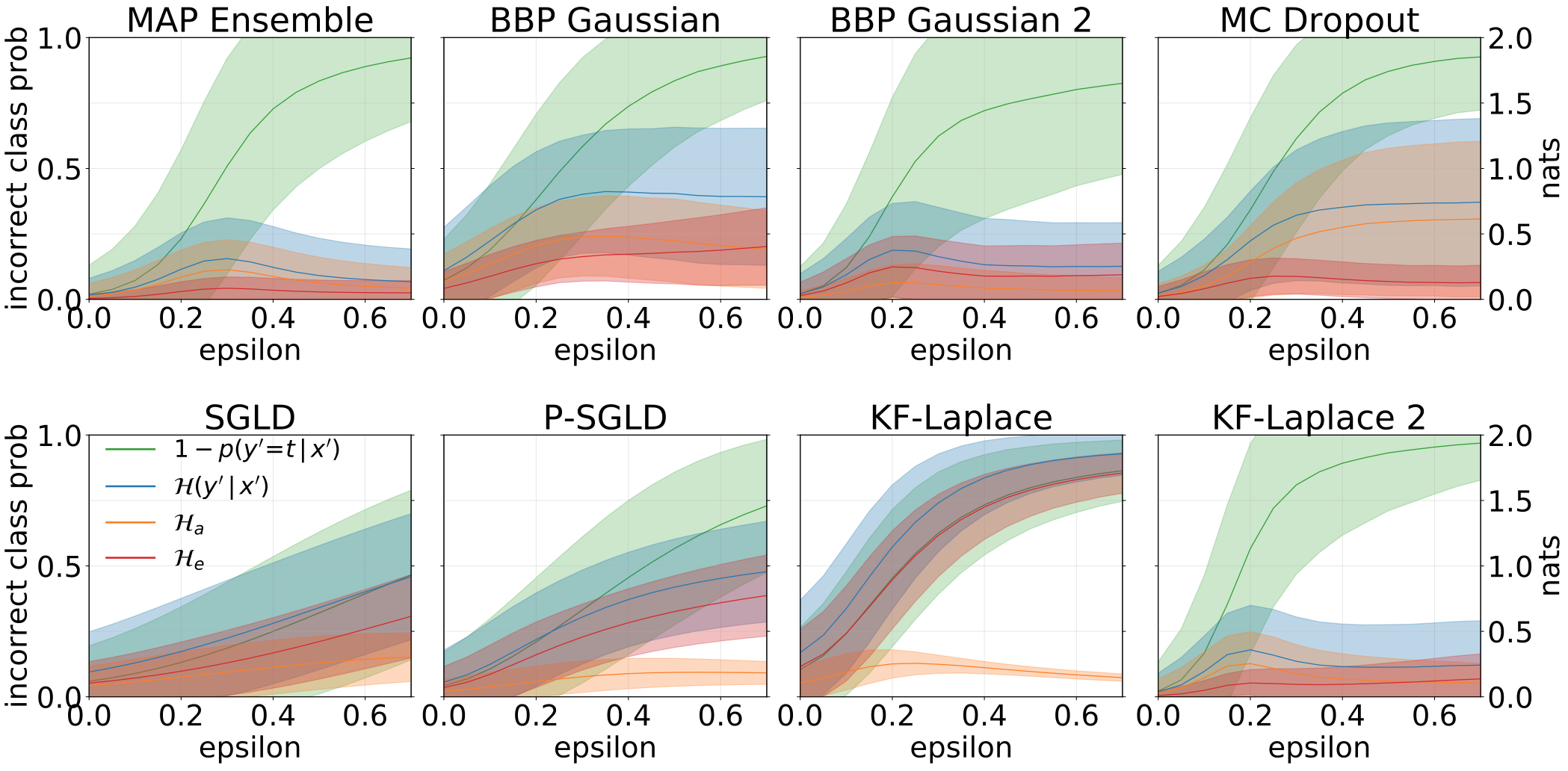
ความไม่แน่นอนทั้งหมด, aleatoric และ epistemic ที่ได้รับเมื่อให้อาหารแบบจำลองของเราด้วยตัวอย่างที่เป็นปฏิปักษ์ (FGSM)
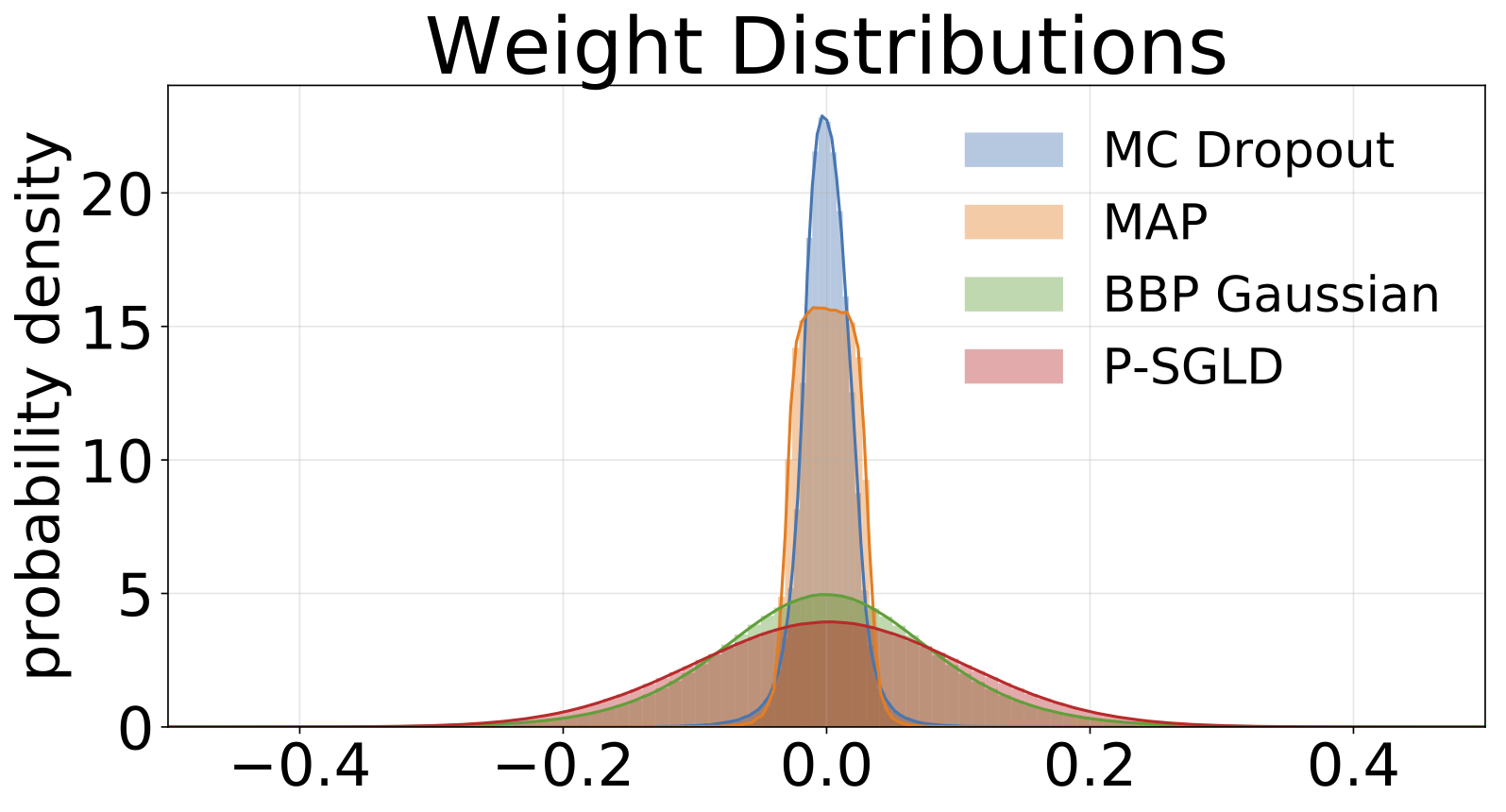
ฮิสโตแกรมของน้ำหนักตัวอย่างจากแต่ละรุ่นที่ผ่านการฝึกอบรมเกี่ยวกับ MNIST เราวาดตัวอย่าง W 10 ตัวอย่างสำหรับแต่ละรุ่น
#Todo