Pytorch -Implementierungen für die folgenden ungefähren Inferenzmethoden:
Wir bieten auch Code für:
Das Projekt ist in Python 2.7 und Pytorch 1.0.1 geschrieben. Wenn CUDA verfügbar ist, wird es automatisch verwendet. Die Modelle können auch auf CPU laufen, da sie nicht übermäßig groß sind.
Wir haben homoskedastische und heteroskedastische Regressionserfahrungen zu Spielzeugdatensätzen durchgeführt, die mit (Gaußschen Prozess der Grundwahrheit) sowie zu realen Daten (sechs UCI -Datensätze) generiert wurden.
Notebooks/Klassifizierung/(Modellname) _ (experimentTyPe) .IPYNB : Enthält Experimente mit (modelname) auf (experimentType), dh homoscedastic/heteroskedastisch. Die heteroskedastischen Notizbücher enthalten sowohl Spielzeug- als auch UCI -Datensatzexperimente für einen bestimmten (Modellname).
Wir stellen auch Google Colab -Notizbücher zur Verfügung. Dies bedeutet, dass Sie auf einer GPU (kostenlos!) Ausführen können. Keine Änderungen erforderlich -alle Abhängigkeiten und Datensätze werden aus den Notebooks hinzugefügt -mit Ausnahme der Auswahl von Laufzeit -> Laufzeittyp ändern -> Hardware Accelerator -> GPU.
train_ (modelName) _ (Datensatz) .py : Züge (modellname) auf (Datensatz). Trainingsmetriken und Modellgewichte werden in den angegebenen Verzeichnissen gespeichert.
SRC/ : Allgemeine Dienstprogramme und Modelldefinitionen.
Notizbücher/Klassifizierung : Eine Asortment von Notizbüchern, die Modelltraining, Bewertung und Ausführung von Unsicherheitsexperimenten der Ziffernrotation ermöglichen. Sie ermöglichen auch die Gewichtsverteilung und das Gewichtsschneiden. Sie ermöglichen die Belastung von vorgeborenen Modellen für das Experimentieren.
(https://arxiv.org/abs/1505.05424)
Colab -Notizbücher mit Regressionsmodellen: BBP homoskedastisch / heteroskedastisch
Trainieren Sie ein Modell auf MNIST:
python train_BayesByBackprop_MNIST.py [--model [MODEL]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Für eine Erklärung der Argumente des Skripts:
python train_BayesByBackprop_MNIST.py -hDie besten Ergebnisse werden mit einem Laplace Prior erzielt.
(https://arxiv.org/abs/1506.02557)
Bayes nach Backprop -Inferenz, bei der der Mittelwert und die Varianz der Aktivierungen in geschlossener Form berechnet werden. Aktivierungen werden anstelle von Gewichten abgetastet. Dies macht die Varianz der Monte -Carlo -ELBO -Schätzungsskala als 1/m, wobei m die Minibatchgröße ist. Probenahmegewichte (M-1)/m. Die KL -Divergenz zwischen Gaußern kann ebenfalls in geschlossener Form berechnet werden, wodurch die Varianz weiter verringert wird. Die Berechnung jeder Epoche ist schneller und die Konvergenz.
Trainieren Sie ein Modell auf MNIST:
python train_BayesByBackprop_MNIST.py --model Local_Reparam [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]](https://arxiv.org/abs/1506.02142)
Eine feste Abbrecherrate von 0,5 wird festgelegt.
Colab -Notizbücher mit Regressionsmodellen: MC -Tropfen homoskedastisch heteroskedastisch
Trainieren Sie ein Modell auf MNIST:
python train_MCDropout_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Für eine Erklärung der Argumente des Skripts:
python train_MCDropout_MNIST.py -h(https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf)
Um in das wahre hintere posterior über w zu konvergieren, sollte die Lernrate gemäß den Robbins-Monro-Bedingungen geglüht werden. In der Praxis verwenden wir eine feste Lernrate.
Colab -Notizbücher mit Regressionsmodellen: SGLD Homoscedastic / Heteroscedasticastic
Trainieren Sie ein Modell auf MNIST:
python train_SGLD_MNIST.py [--use_preconditioning [USE_PRECONDITIONING]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Für eine Erklärung der Argumente des Skripts:
python train_SGLD_MNIST.py -h(https://arxiv.org/abs/1512.07666)
SGLD mit RMSProp -Vorkonditionierung. Eine höhere Lernrate sollte verwendet werden als für Vanille -SGLD.
Trainieren Sie ein Modell auf MNIST:
python train_SGLD_MNIST.py --use_preconditioning True [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Mehrere Netzwerke werden auf Teilproben des Datensatzes geschult.
Colab -Notizbücher mit Regressionsmodellen: Karten -Ensemble homoskedastisch / heteroskedastisch
Trainieren Sie ein Ensemble auf MNIST:
python train_Bootrap_Ensemble_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--subsample [SUBSAMPLE]] [--n_nets [N_NETS]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Für eine Erklärung der Argumente des Skripts:
python train_Bootrap_Ensemble_MNIST.py -h(https://openreview.net/pdf?id=Skdvd2xaz)
Trainieren Sie ein Kartennetz und berechnen Sie dann eine Taylor -Serie zweiter Ordnung mit der Krümmung um einen Modus des hinteren. Es wird eine blockdiagonale hessische Näherung verwendet, bei der nur intra-Schicht-Abhängigkeiten berücksichtigt werden. Der Hessische wird als Kronecker -Produkt der Erwartung der hessischen Faktoren eines einzelnen DataPoint weiter angenähert. Das Annäherung an den Hessischen kann eine Weile dauern. Zum Glück muss es nur einmal gemacht werden.
Trainieren Sie ein Kartennetz auf MNIST und ungefähres Hessian:
python train_KFLaplace_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--hessian_diag_sig [HESSIAN_DIAG_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Für eine Erklärung der Argumente des Skripts:
python train_KFLaplace_MNIST.py -hBeachten Sie, dass wir die nicht skalierten und unbeschreiblichen hessischen Faktoren speichern. Dies ermöglicht rechnerisch billige Änderungen an der Prior-Zeit zum Inferenzzeit, da der Hessische nicht erneut berechnet werden muss. Inferenz erfordert die Umkehrung der angenäherten hessischen Faktoren und die Stichproben aus einer Matrixnormalverteilung. Dies ist in Notebooks/kfac_laplace_mnist.ipynb gezeigt
(https://arxiv.org/abs/1402.4102)
Wir implementieren die skalierungsbedingte Version dieses Algorithmus, die hier vorgeschlagen wurde, um Hyperparameter beim Burn-In automatisch zu finden. Wir platzieren einen Gaußschen früheren Netzwerkgewichte und einen Gamma -Hyperprior über die Präzision des Gaußschen.
Führen Sie SG-HMC-SA Burn In und Sampler aus und speichern Sie Gewichte in der angegebenen Datei.
python train_SGHMC_MNIST.py [--epochs [EPOCHS]] [--sample_freq [SAMPLE_FREQ]] [--burn_in [BURN_IN]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Für eine Erklärung der Argumente des Skripts:
python train_SGHMC_MNIST.py -hMAP -Inferenz liefert eine Punktschätzung der Parameterwerte. Wenn diese Modelle aus Verteilungseingängen wie rotierten Ziffern ausgesetzt sind, machen diese Modelle mit hohem Vertrauen falsche Vorhersagen.
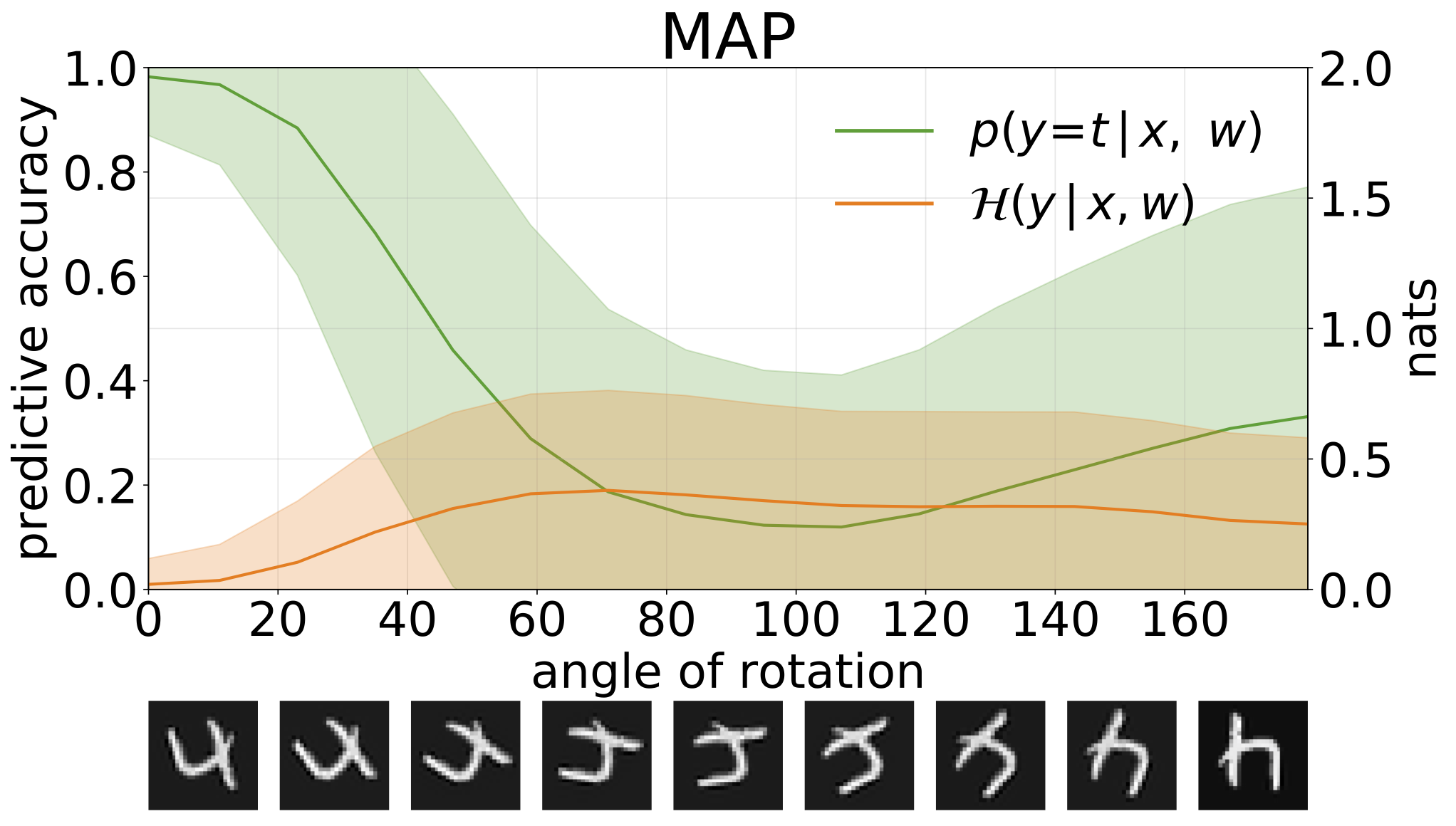
Wir können die Unsicherheit in den Vorhersagen unserer Modelle durch prädiktive Entropie messen. Wir können diesen Begriff zersetzen, um zwischen 2 Arten von Unsicherheiten zu unterscheiden. Unsicherheit, die durch Rauschen in den Daten oder die aleatorische Unsicherheit verursacht werden, kann als erwartete Entropie der Modellvorhersagen quantifiziert werden. Modellunsicherheit oder epistemische Unsicherheit kann als Differenz zwischen Gesamtentropie und aleatorischer Entropie gemessen werden.
Spielzeug homoskedastische Regressionsaufgabe. Die Daten werden von einem GP mit einem RBF -Kernel (L = 1, σn = 0,3) generiert. Wir verwenden ein einzelnes FC-Netzwerk mit einer versteckten Schicht von 200 Relu-Einheiten, um das Regressionsmittelwert μ (x) vorherzusagen. Ein festes Protokoll σ wird separat gelernt.
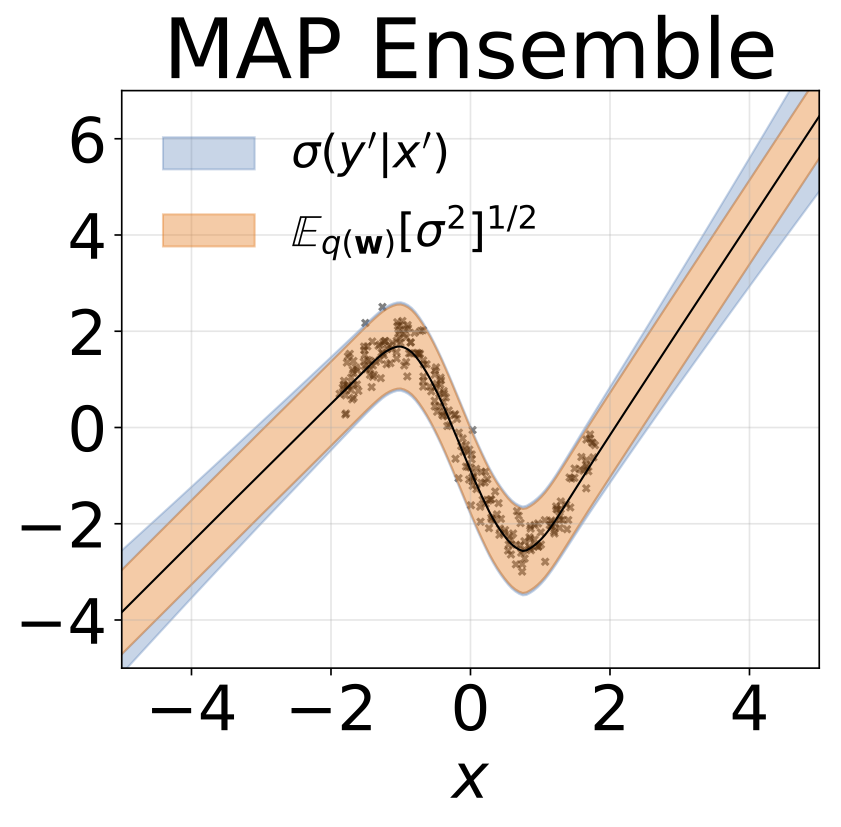
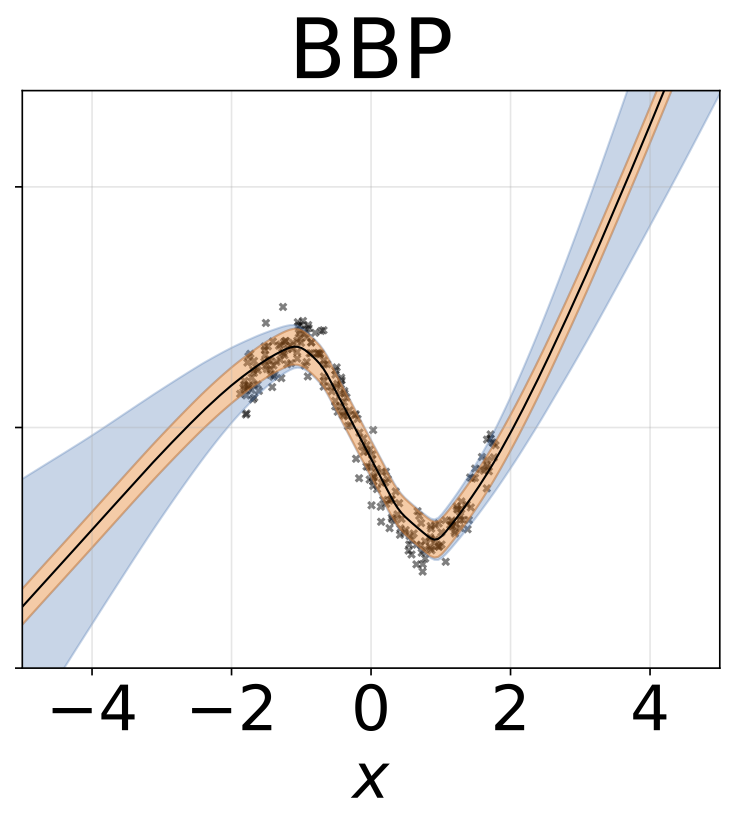
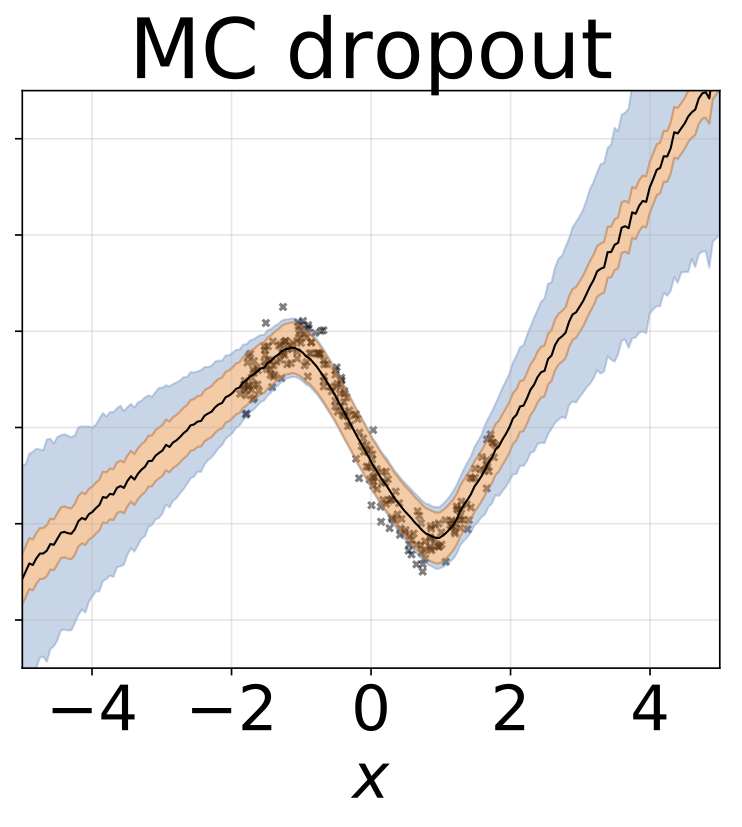
Das gleiche Szenario wie der vorherige Abschnitt, aber log σ (x) wird aus der Eingabe vorhergesagt.
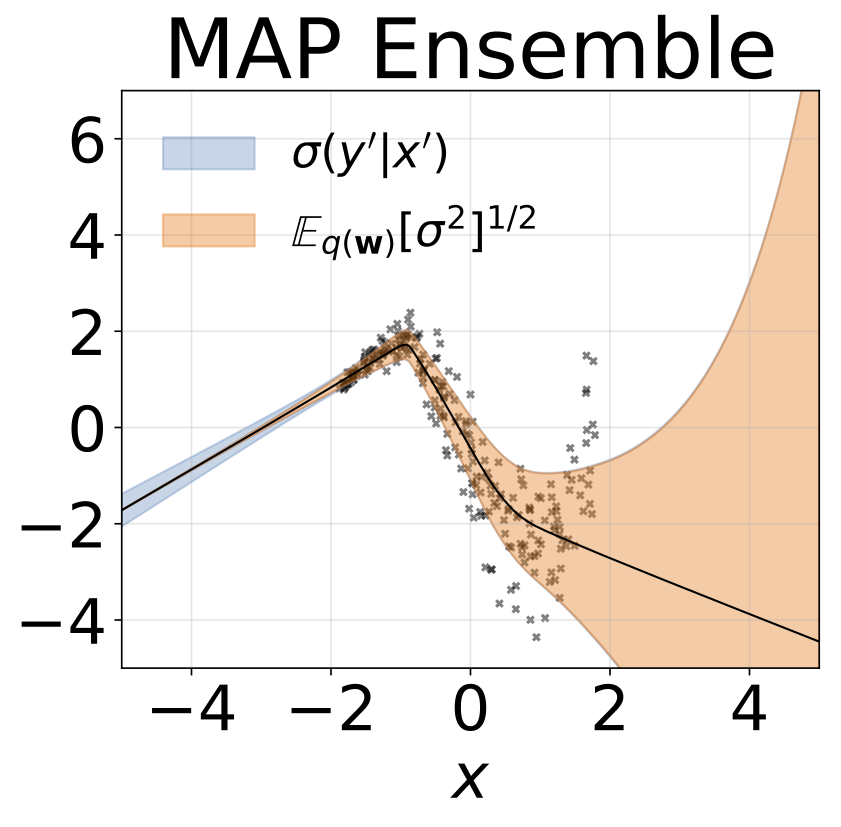
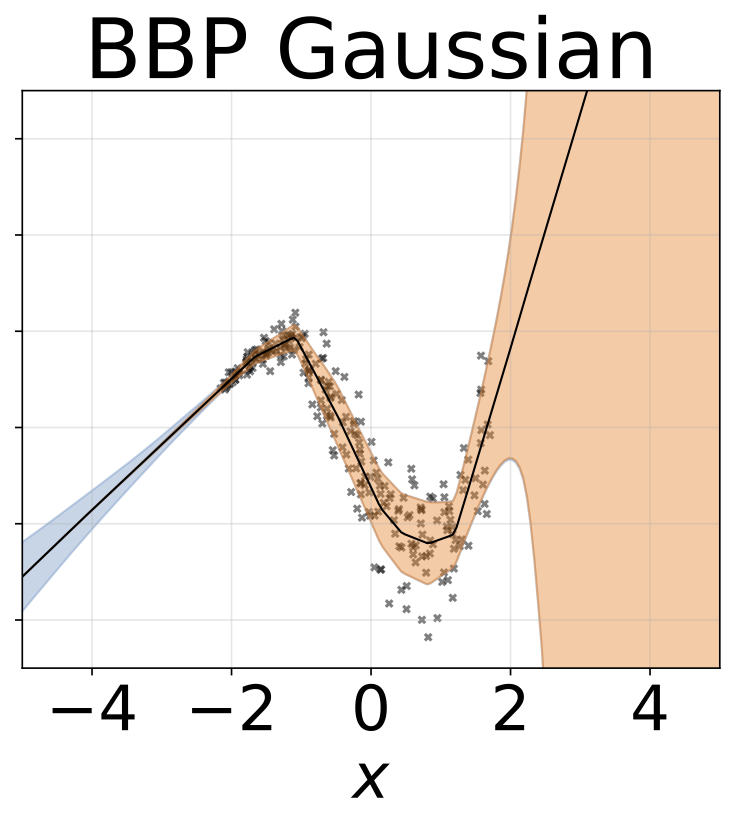
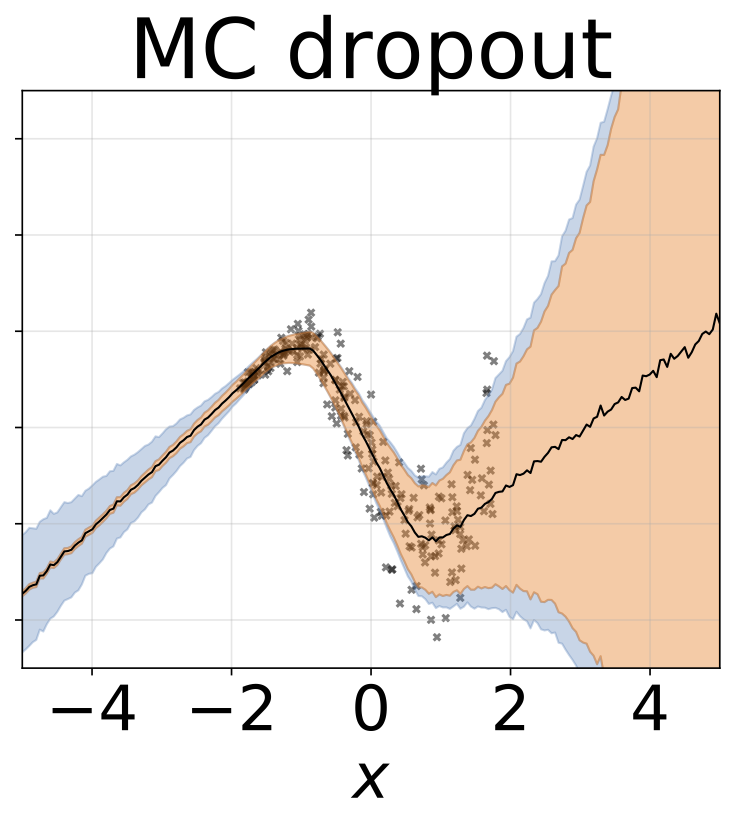
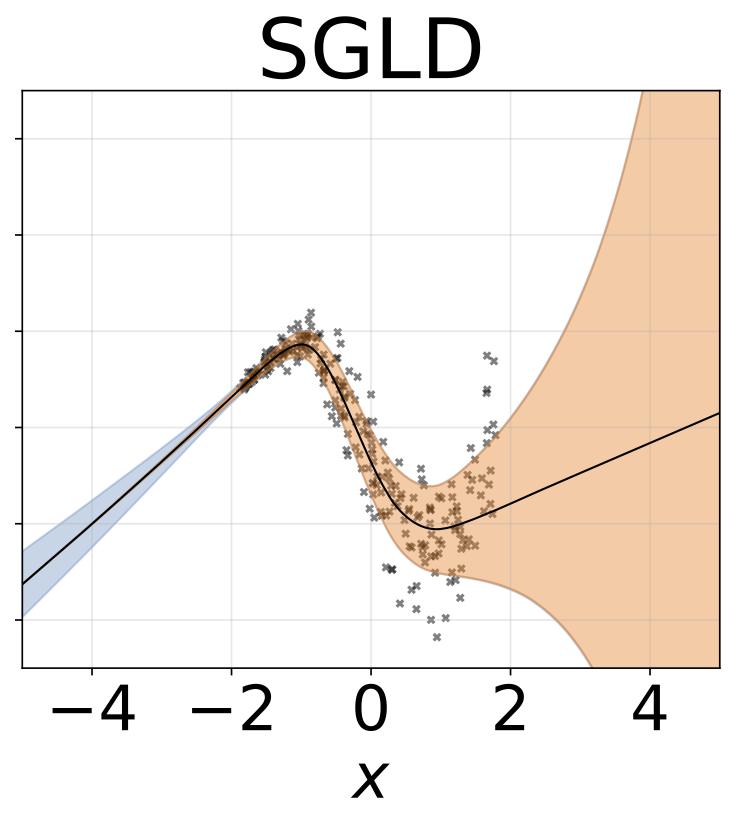
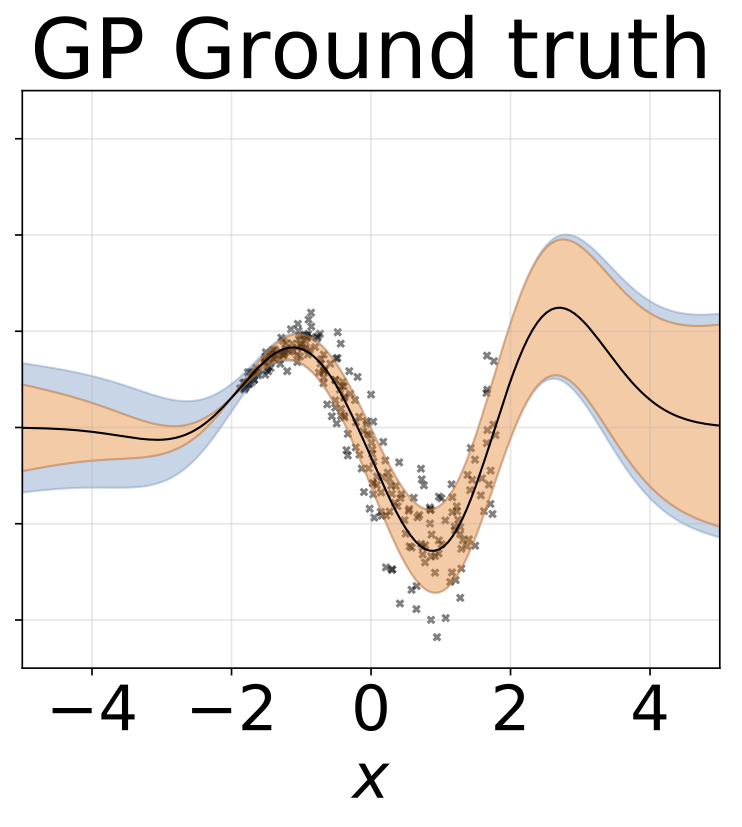
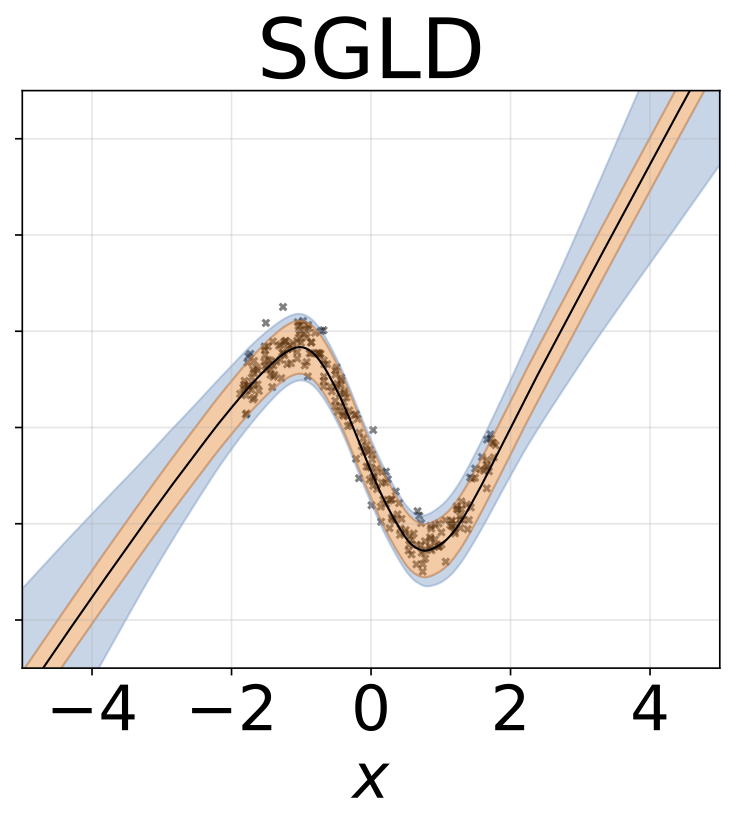
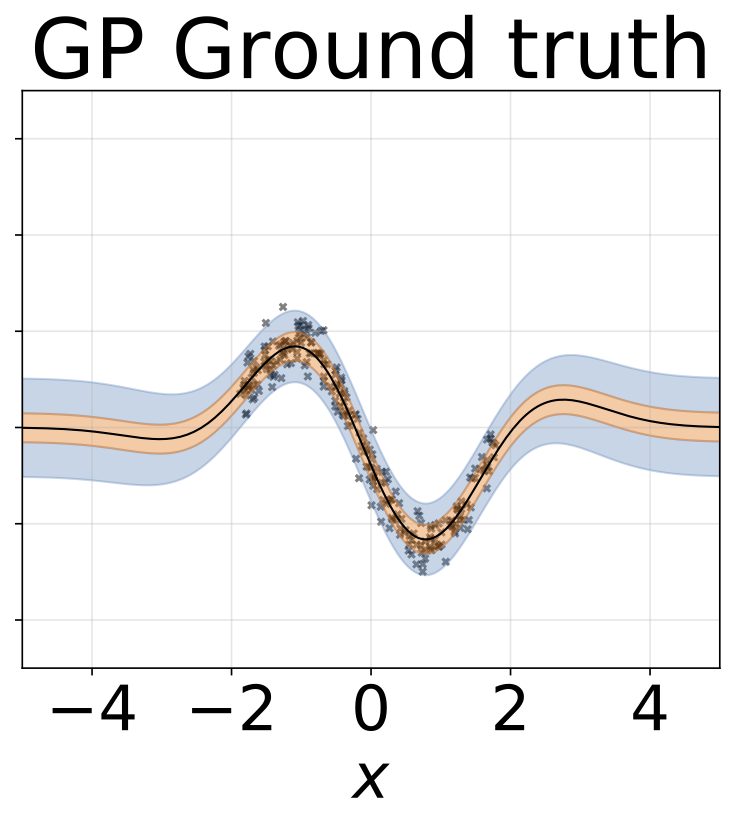
Heteroskedastische Regressionsaufgabe mit Spielzeug. Die Daten werden von einem GP mit einem RBF -Kernel erzeugt (L = 1 σn = 0,3 · | x + 2 |). Wir verwenden ein Zweiköpfungsnetzwerk mit 200 Relu-Einheiten, um das Regressionsmittelwert μ (x) und das logarithmische Abweichungsprotokoll σ (x) vorherzusagen.
Wir führten eine heteroskedastische Regression in den sechs UCI-Datensätzen (Gehäuse, Beton, Energieeffizienz, Kraftwerk, Rotwein und Yacht-Datensätze) unter Verwendung von 10-Foild-Kreuzvalidierung durch. Alle diese Experimente sind in den heteroskedastischen Notizbüchern enthalten. Beachten Sie, dass die Ergebnisse stark von der Hyperparameterauswahl abhängen. Die folgenden Diagramme zeigen Log-Likelihoods und RMSS im Zug (semi-transparente Farbe) und Test (feste Farbe). Kreise und Fehlerbalken entsprechen dem 10-fachen Quervalidierungsmittelwert bzw. Standardabweichungen.
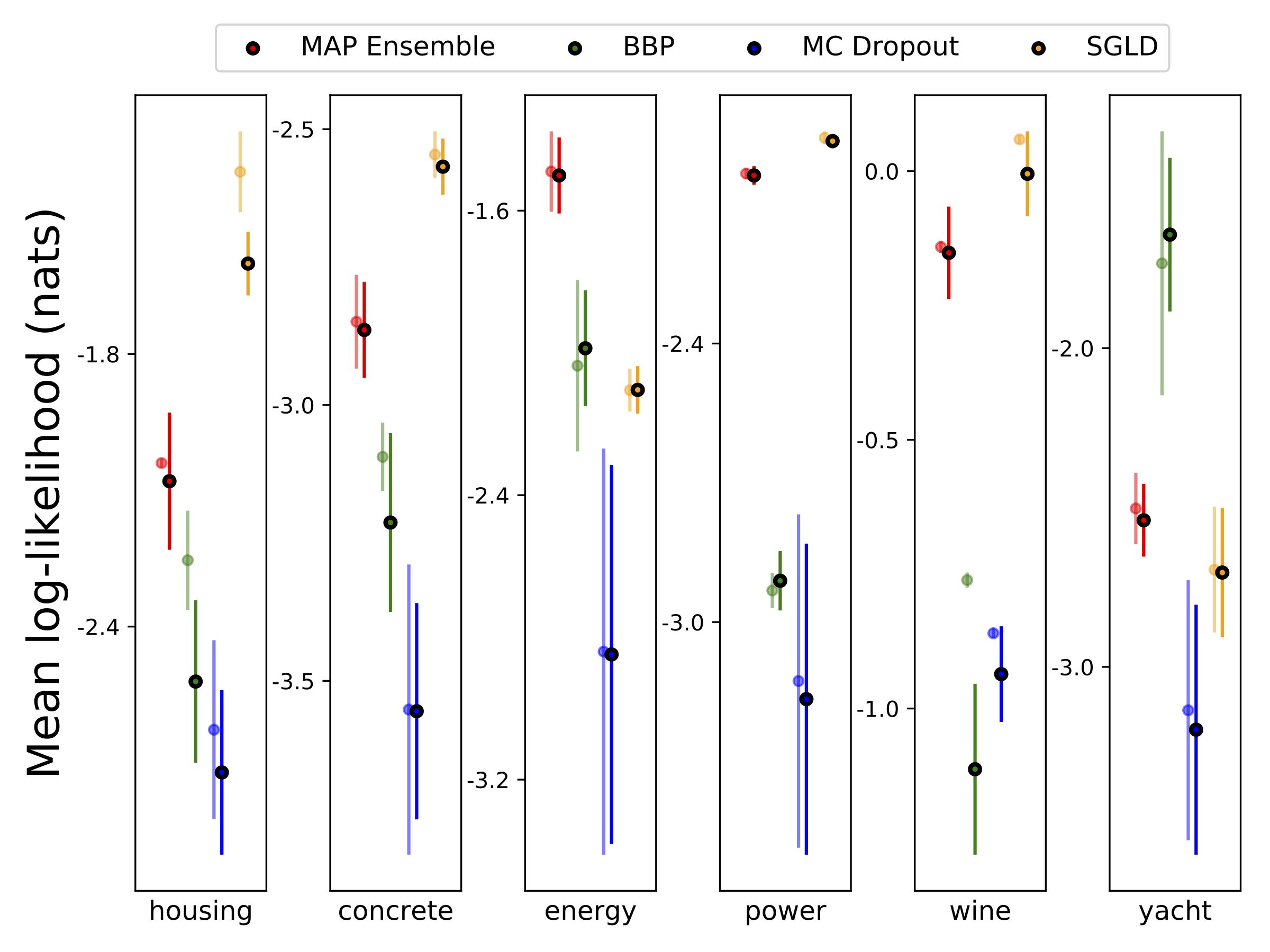
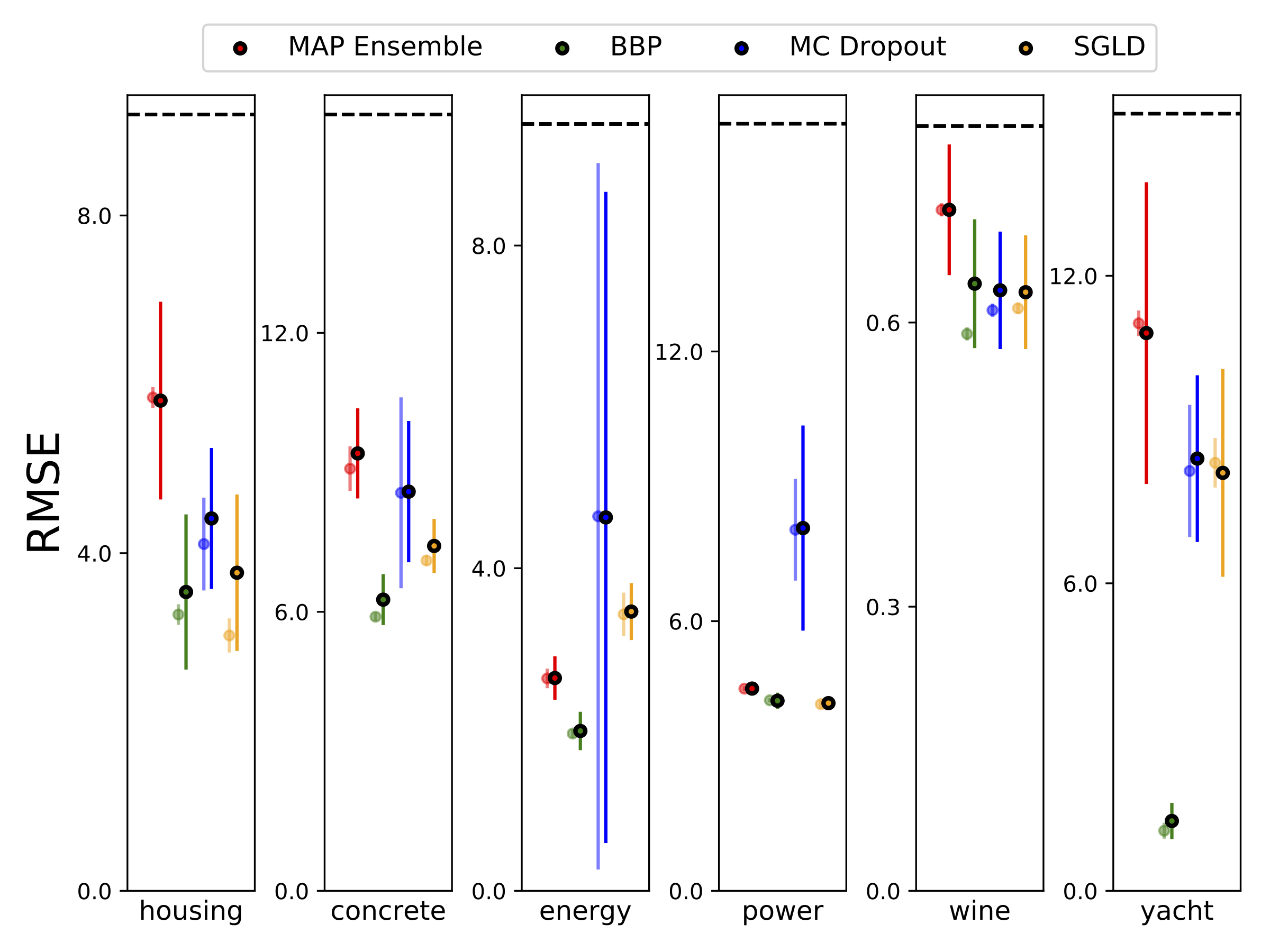
W wird mit 100 Proben der Gewichte für alle Modelle außer MAP marginalisiert, wobei nur ein Satz Gewichte verwendet wird.
| MNIST -Test | KARTE | Kartensemble | BBP Gaußsisch | BBP GMM | BBP Laplace | BBP Local Reparam | MC Dropout | SGLD | PSGLD |
|---|---|---|---|---|---|---|---|---|---|
| Log wie | -572.9 | -496.54 | -1100.29 | -1008.28 | -892.85 | -1086.43 | -435.458 | -828.29 | -661.25 |
| Fehler % | 1,58 | 1,53 | 2.60 | 2.38 | 2.28 | 2.61 | 1.37 | 1.76 | 1.76 |
MNIST -Testergebnisse für in Betracht gezogene Methoden. Es wurde noch nicht die estentenhyperparameter -Tunning durchgeführt. Wir approximieren die hintere Vorhersageverteilung mit 100 MC -Proben. Wir verwenden ein FC -Netzwerk mit zwei Relu -Schichten von 1200 Einheiten. Bei nicht spezifiziertem Prior ist Gaußsisch mit STD = 0,1. P-SGLD verwendet eine RMSProp-Vorkonditionierung.
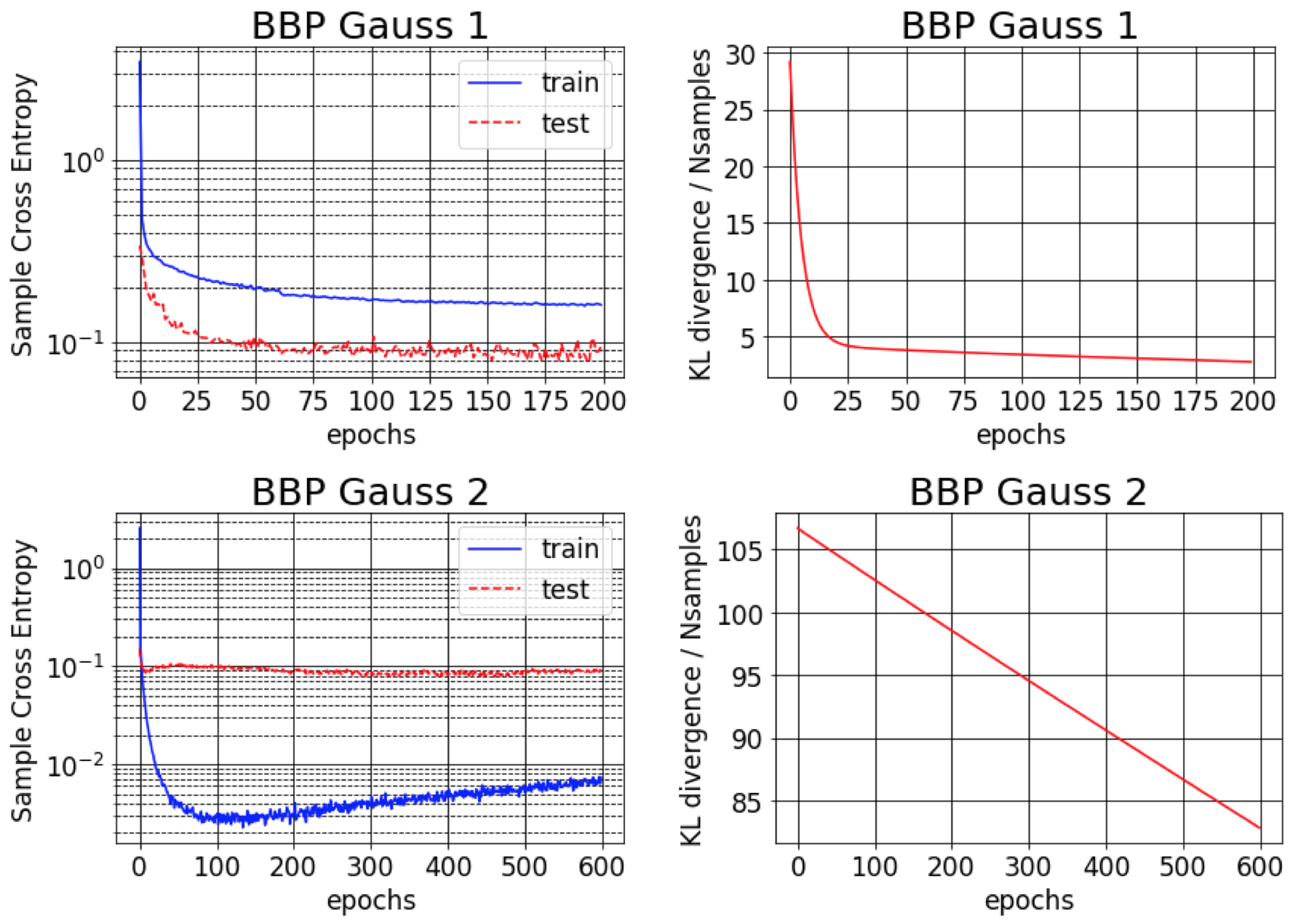
Das Originalpapier für Bayes By Backprop meldet einen Fehler von rund 1% bei MNIST. Wir stellen fest, dass dieses Ergebnis nur erreichbar ist, wenn ungefähre hintere Abweichungen als sehr klein (BBP Gauß 2) initialisiert werden. In diesem Szenario ähneln die Verteilungen über Gewichte Deltas und bieten eine gute prädiktive Leistung, aber schätzende Unsicherheitsschätzungen. Wenn wir jedoch die Varianzen für die Prior (BBP Gauß 1) initialisieren, erhalten wir die obigen Ergebnisse. Die Trainingskurven für diese beiden Hyperparameter -Konfigurationsschemata sind unten gezeigt:
Total-, aleatorische und epistemische Unsicherheiten, die bei der Erstellung von OOD -Proben erhalten wurden, indem der MNIST -Testsatz mit Rotationen erweitert wird:
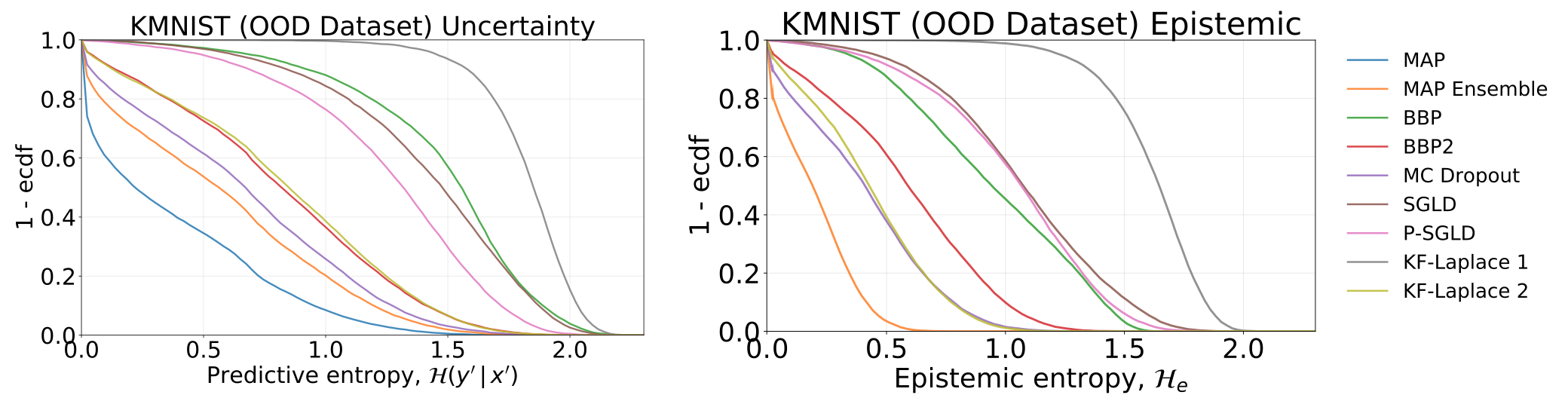
Gesamt- und epistemische Unsicherheiten, die durch das Testen unserer Modelle, die auf MNIST geschult wurden, erhalten wurden, auf dem KMNIST -Datensatz:
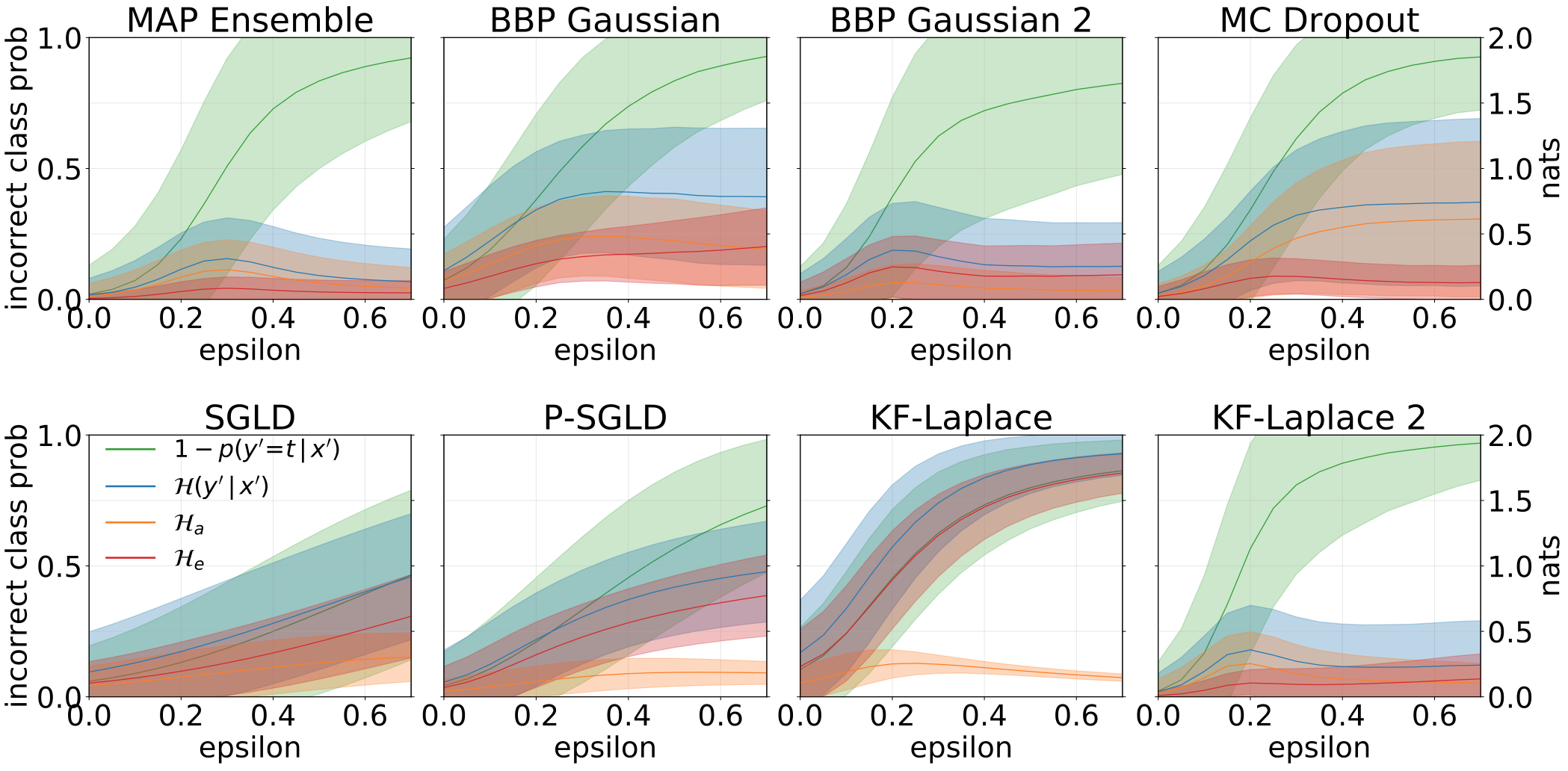
Gesamt-, aleatorische und epistemische Unsicherheiten, die bei der Fütterung unserer Modelle mit widersprüchlichen Proben (FGSM) erhalten wurden.
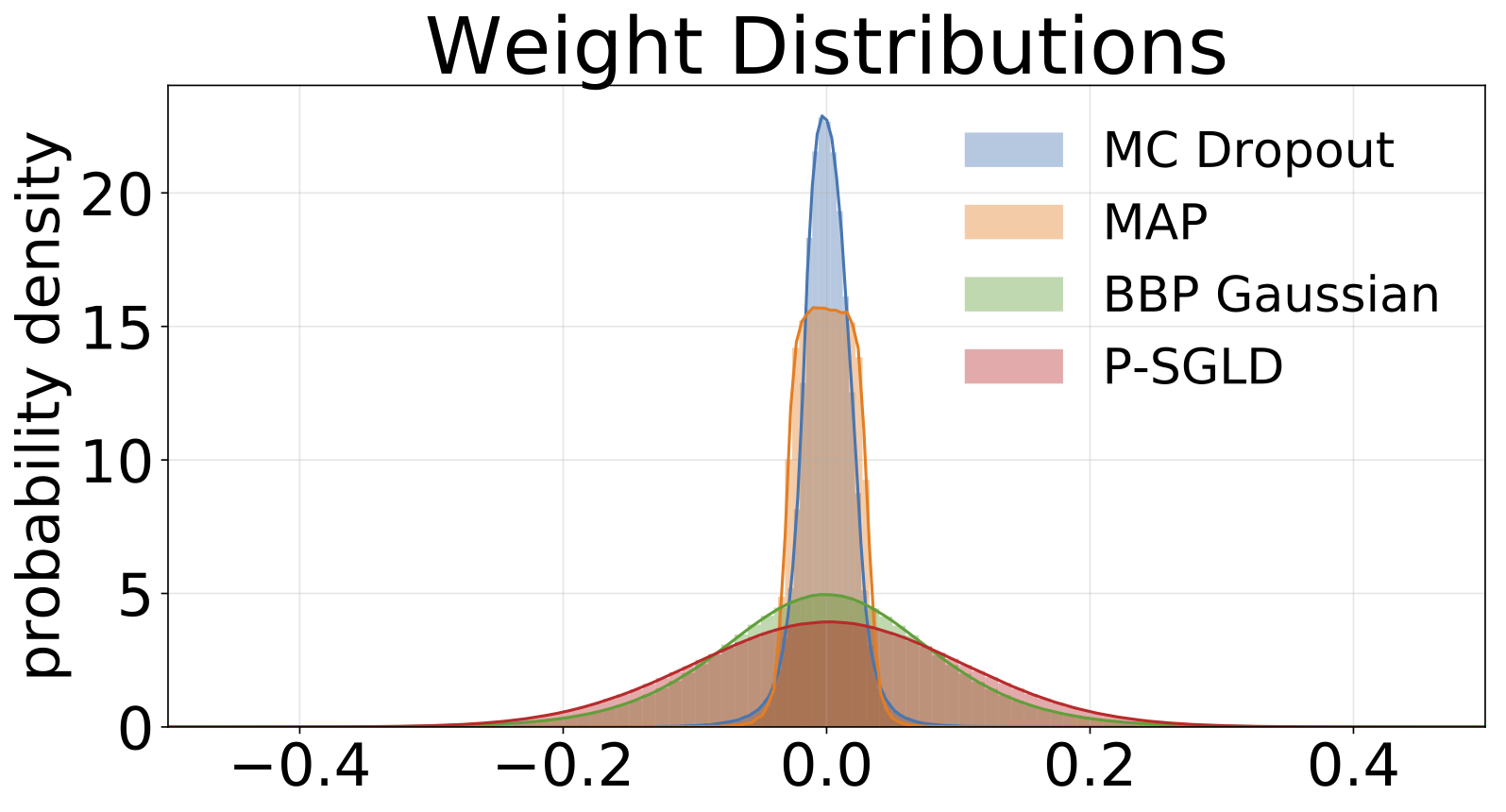
Histogramme von Gewichten, die aus jedem auf MNIST trainierten Modell abgetastet wurden. Wir zeichnen 10 Proben von W für jedes Modell.
#Todo