Implementações de Pytorch para os seguintes métodos aproximados de inferência:
Também fornecemos código para:
O projeto está escrito no Python 2.7 e Pytorch 1.0.1. Se o CUDA estiver disponível, ele será usado automaticamente. Os modelos também podem ser executados na CPU, pois não são excessivamente grandes.
Realizamos experiências de regressão homoscedásticas e heterocedásticas em conjuntos de dados de brinquedos, gerados com (Processo Gaussian, true fundamental), bem como em dados reais (seis conjuntos de dados da UCI).
Notebooks/Classificação/(ModelName) _ (ExperyType) .IPynb : Contém experimentos usando (ModelName) no (Experimentype), ou seja, homosdedastic/heteroscedástico. Os notebooks heterocedásticos contêm experimentos de conjunto de dados de brinquedo e UCI para um determinado (ModelName).
Também fornecemos notebooks do Google Colab. Isso significa que você pode executar em uma GPU (de graça!). Não são necessárias modificações -todas as dependências e conjuntos de dados são adicionados dentro dos notebooks -exceto para selecionar o tempo de execução -> Alterar o Type de tempo de execução -> Acelerador de hardware -> GPU.
TRIN_ (ModelName) _ (DataSet) .py : trens (ModelName) ON (DataSet). Métricas de treinamento e pesos do modelo serão salvos nos diretórios especificados.
SRC/ : Utilitários gerais e definições de modelo.
Notebooks/Classificação : Um coletor de notebooks que permitem treinamento para modelos, avaliação e execução de experimentos de incerteza de rotação de dígitos. Eles também permitem a plotagem de distribuição de peso e a poda de peso. Eles permitem o carregamento de modelos pré-treinados para experimentação.
(https://arxiv.org/abs/1505.05424)
Notebooks colab com modelos de regressão: BBP homoscedástico / heterocedástico
Treine um modelo no mnist:
python train_BayesByBackprop_MNIST.py [--model [MODEL]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para uma explicação dos argumentos do roteiro:
python train_BayesByBackprop_MNIST.py -hOs melhores resultados são obtidos com um Laplace antes.
(https://arxiv.org/abs/1506.02557)
Bayes por inferência de backprop, onde a média e a variação das ativações são calculadas em forma fechada. As ativações são amostradas em vez de pesos. Isso torna a variação da escala do estimador de Monte Carlo Elbo como 1/m, onde M é o tamanho do minibatch. Escalas de pesos de amostragem (m-1)/m. A divergência de KL entre gaussianos também pode ser calculada em forma fechada, reduzindo ainda mais a variação. O cálculo de cada época é mais rápido e a convergência também.
Treine um modelo no mnist:
python train_BayesByBackprop_MNIST.py --model Local_Reparam [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]](https://arxiv.org/abs/1506.02142)
Uma taxa de abandono fixa de 0,5 está definida.
Notebooks colab com modelos de regressão: MC abandonando heterocedástico homoscedástico
Treine um modelo no mnist:
python train_MCDropout_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para uma explicação dos argumentos do roteiro:
python train_MCDropout_MNIST.py -h(https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf)
Para convergir para o verdadeiro posterior sobre W, a taxa de aprendizado deve ser recozida de acordo com as condições de Robbins-Monro. Na prática, usamos uma taxa de aprendizado fixa.
Notebooks colab com modelos de regressão: SGLD homoscedástico / heterocedástico
Treine um modelo no mnist:
python train_SGLD_MNIST.py [--use_preconditioning [USE_PRECONDITIONING]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para uma explicação dos argumentos do roteiro:
python train_SGLD_MNIST.py -h(https://arxiv.org/abs/1512.07666)
SGLD com pré -condicionamento RMSPROP. Uma taxa de ensino superior deve ser usada do que para SGLD de baunilha.
Treine um modelo no mnist:
python train_SGLD_MNIST.py --use_preconditioning True [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Várias redes são treinadas em subamostras do conjunto de dados.
Notebooks colab com modelos de regressão: mapa homoscedástico / heterocedástico
Treine um conjunto no mnist:
python train_Bootrap_Ensemble_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--subsample [SUBSAMPLE]] [--n_nets [N_NETS]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para uma explicação dos argumentos do roteiro:
python train_Bootrap_Ensemble_MNIST.py -h(https://openreview.net/pdf?id=skdvd2xaz)
Treine uma rede de mapa e calcule uma série Taylor de segunda ordem Aproxiamtion para a curvatura em torno de um modo do posterior. Uma aproximação hessiana diagonal é usada, onde apenas as dependências intra-camadas são contabilizadas. O Hessian é aproxima -se ainda mais como o produto Kronecker da expectativa de fatores hessianos de um único datapoint. Aproximando -se do Hessiano pode demorar um pouco. Felizmente, isso só precisa ser feito uma vez.
Treine uma rede de mapa no MNIST e aproximadamente Hessian:
python train_KFLaplace_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--hessian_diag_sig [HESSIAN_DIAG_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para uma explicação dos argumentos do roteiro:
python train_KFLaplace_MNIST.py -hObserve que salvamos os fatores hessianos sem escalas e não invasores. Isso permitirá alterações computacionalmente baratas no tempo anterior de inferência, pois o Hessiano não precisará ser recomputado. A inferência exigirá inverter os fatores hessianos aproximados e a amostragem de uma distribuição normal da matriz. Isso é mostrado no Notebooks/kfac_laplace_mnist.ipynb
(https://arxiv.org/abs/1402.4102)
Implementamos a versão em escala adaptada desse algoritmo, proposto aqui para encontrar hiperparâmetros automaticamente durante a queima. Colocamos um gaussiano anterior aos pesos da rede e um hiperpriador gama sobre a precisão do gaussiano.
Execute sg-hmc-sa queima e amostrador, economizando pesos no arquivo especificado.
python train_SGHMC_MNIST.py [--epochs [EPOCHS]] [--sample_freq [SAMPLE_FREQ]] [--burn_in [BURN_IN]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para uma explicação dos argumentos do roteiro:
python train_SGHMC_MNIST.py -hA inferência do mapa fornece uma estimativa pontual dos valores dos parâmetros. Quando fornecidos com entradas fora da distribuição, como dígitos rotacionados, esses modelos fazem previsões erradas com alta confiança.
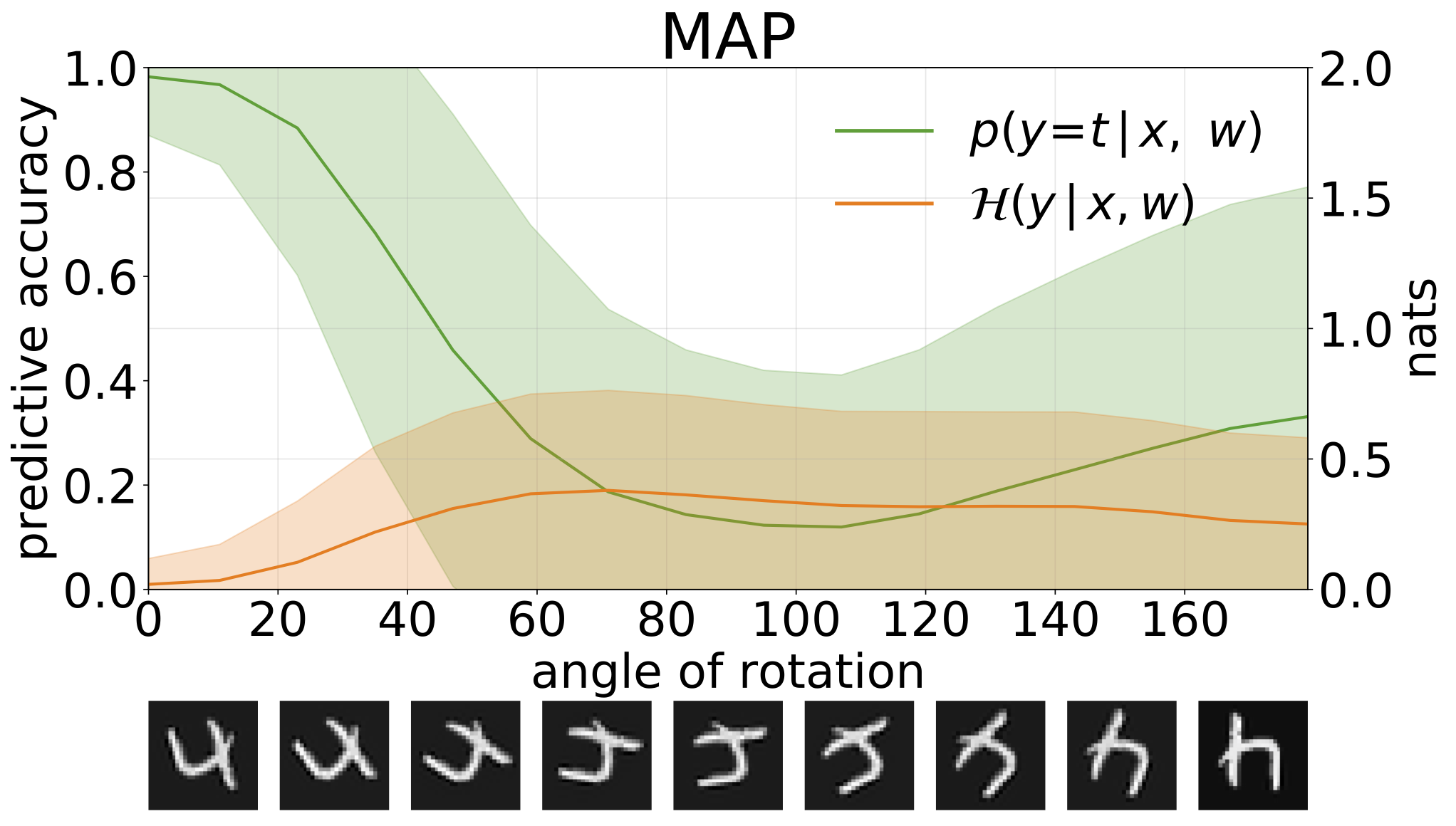
Podemos medir a incerteza nas previsões de nossos modelos por meio de entropia preditiva. Podemos decompor esse termo para distinguir entre 2 tipos de incerteza. A incerteza causada por ruído nos dados, ou incerteza aleatórica , pode ser quantificada como a entropia esperada das previsões do modelo. A incerteza do modelo ou a incerteza epistêmica pode ser medida como a diferença entre entropia total e entropia aleatórica.
Tarefa de regressão homosdedástica de brinquedo. Os dados são gerados por um GP com um kernel RBF (L = 1, σn = 0,3). Utilizamos uma rede FC de saída única com uma camada oculta de 200 unidades RelU para prever a média de regressão μ (x). Um log fixo σ é aprendido separadamente.
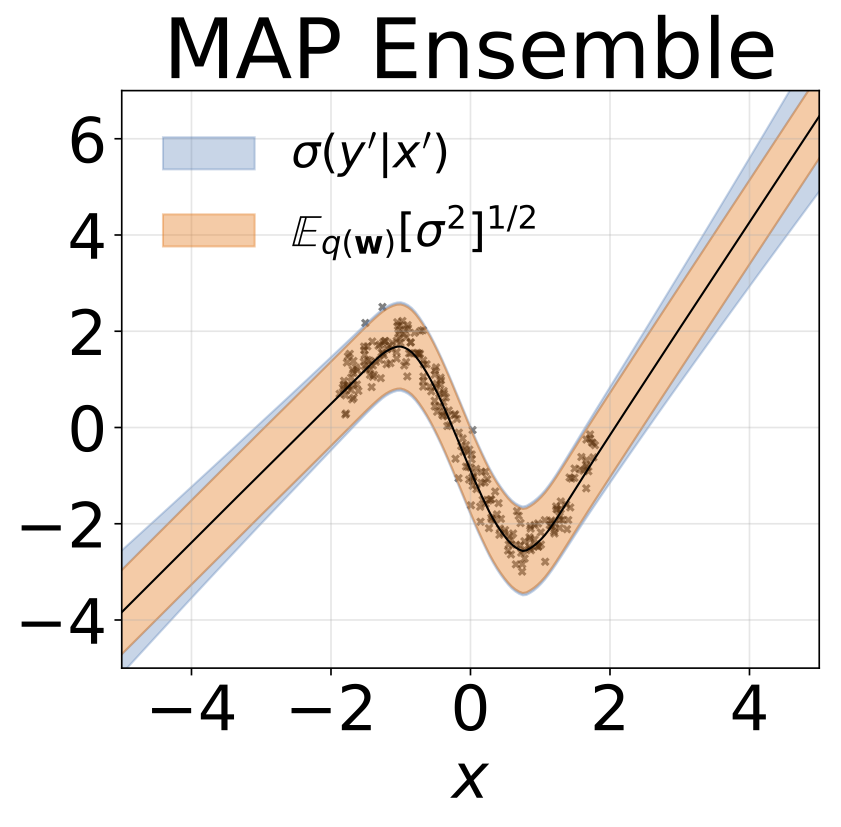
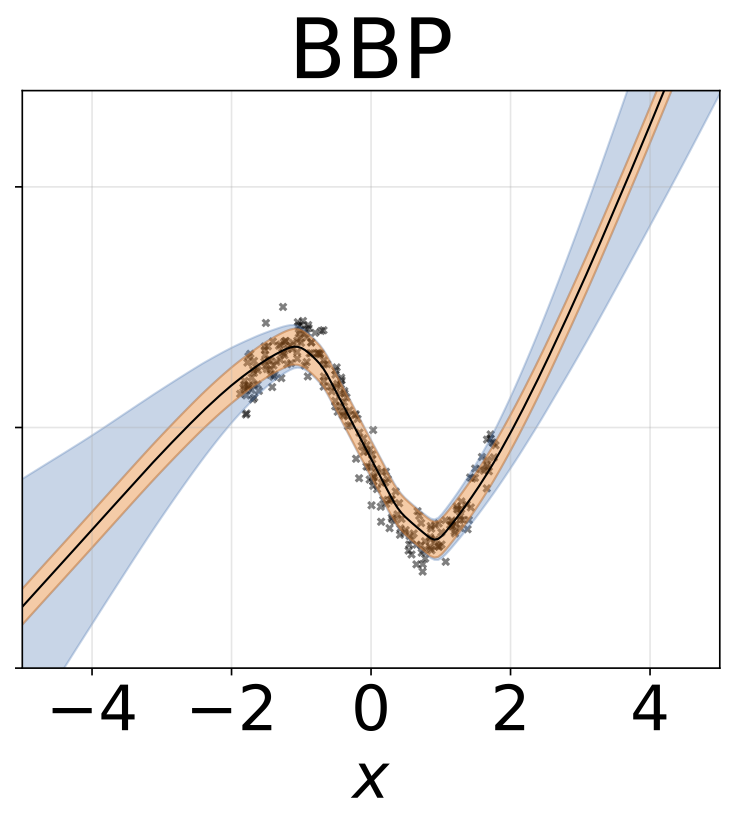
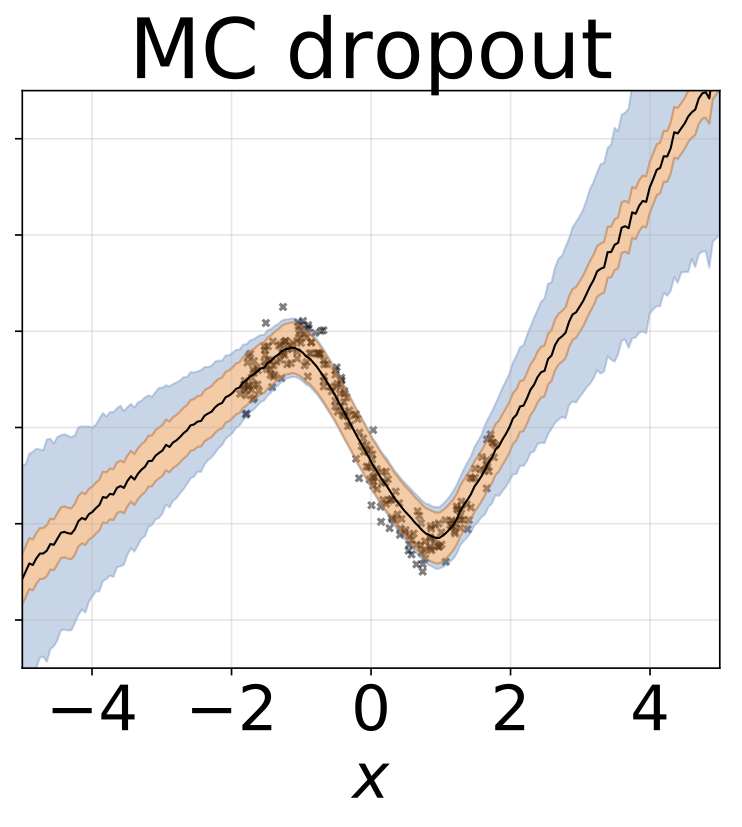
O mesmo cenário da seção anterior, mas o log σ (x) é previsto a partir da entrada.
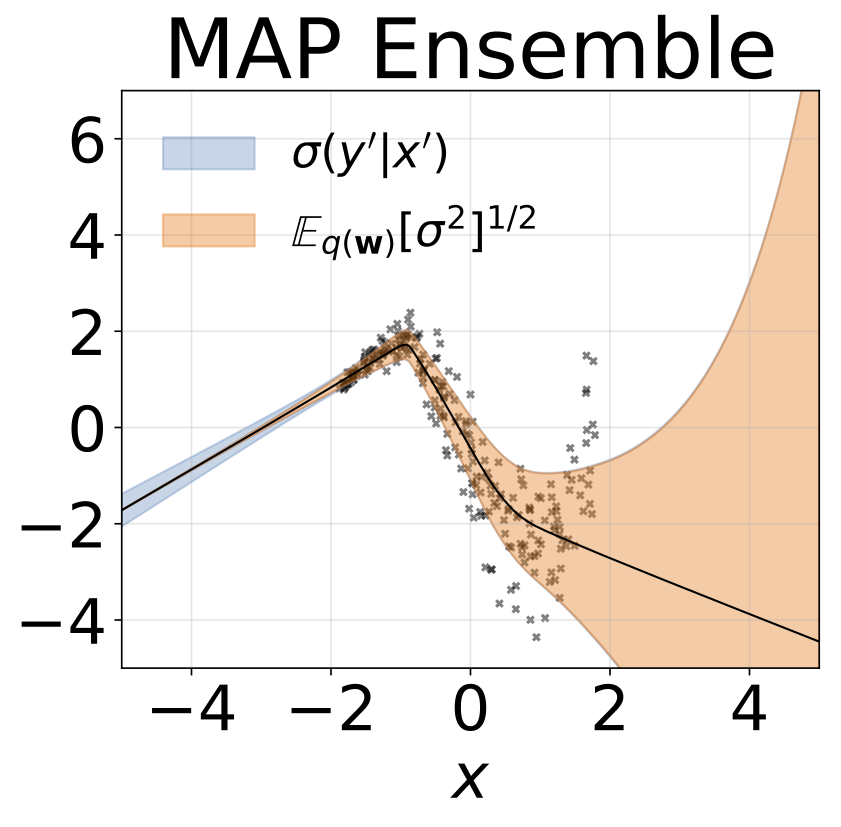
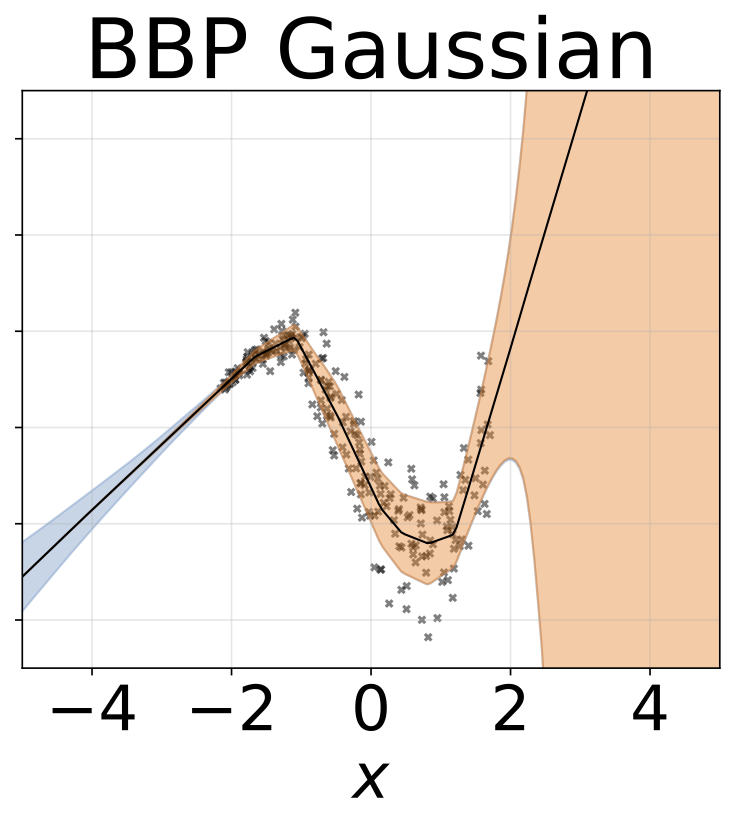
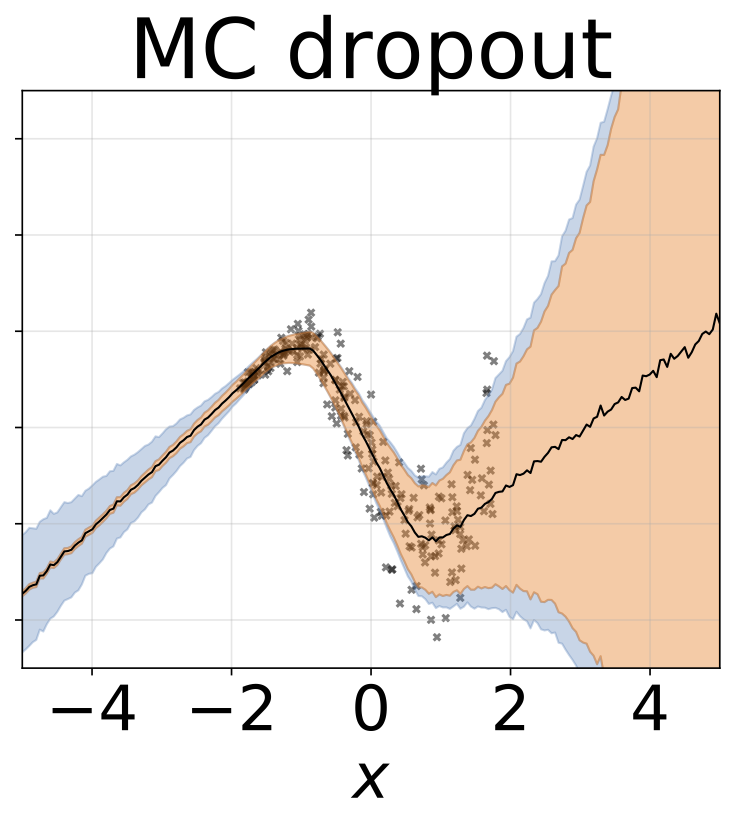
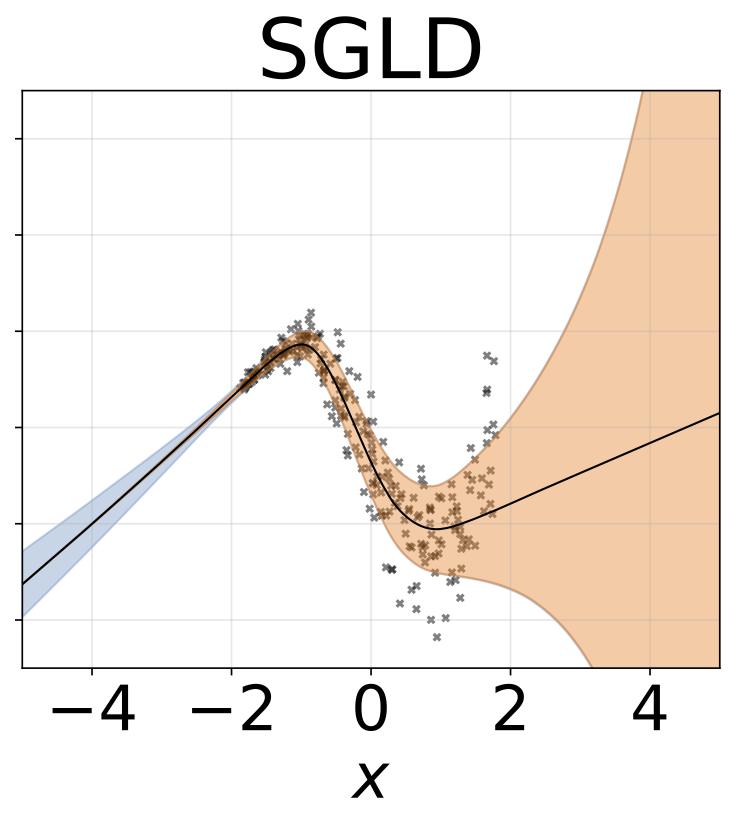
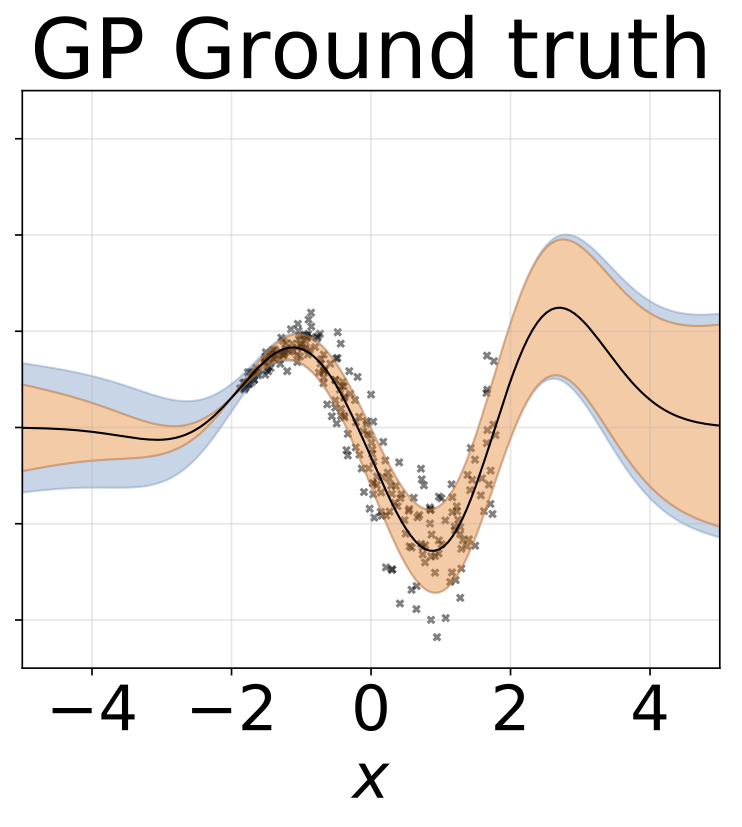
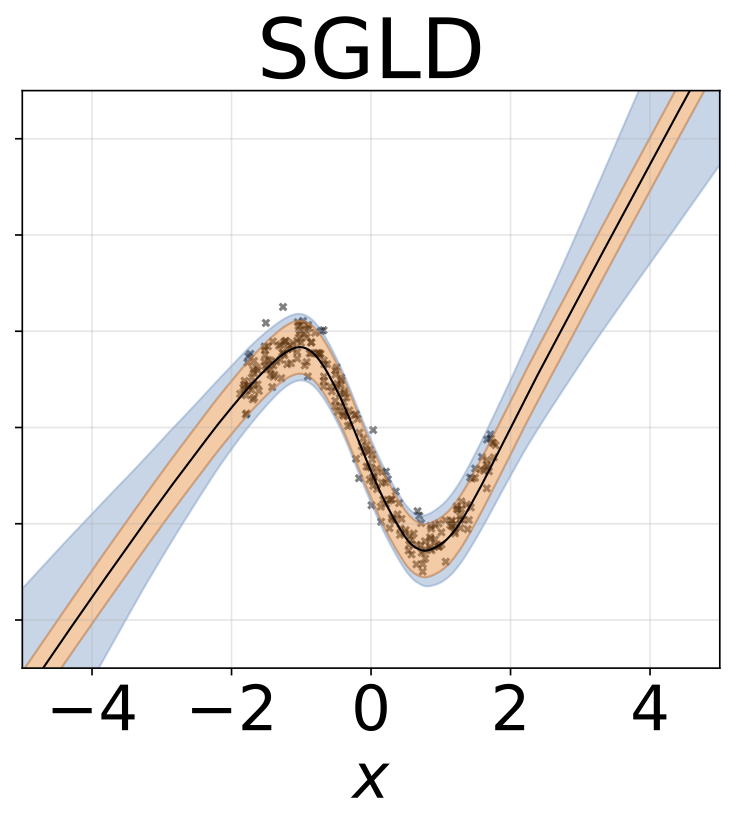
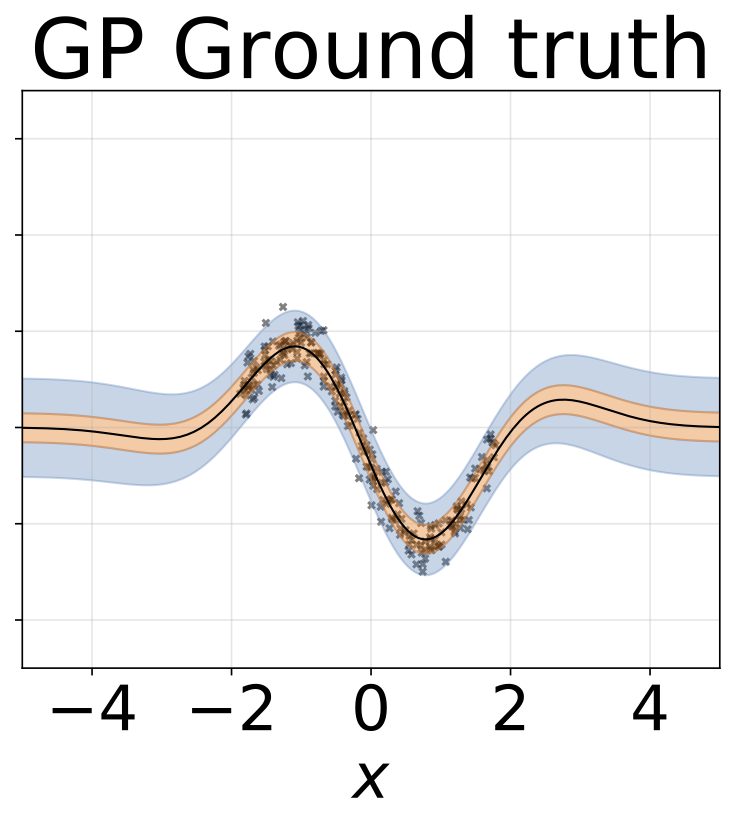
Tarefa de regressão heterocedástica de brinquedo. Os dados são gerados por um GP com um kernel RBF (L = 1 σn = 0,3 · | x + 2 |). Utilizamos uma rede de duas cabeças com 200 unidades RelU para prever a média de regressão μ (x) e log de desvio padrão do log σ (x).
Realizamos a regressão heterocedástica nos seis conjuntos de dados UCI (habitação, concreto, eficiência energética, usina, vinho tinto e conjuntos de dados de iate), usando a validação cruzada de 10 fontes. Todas essas experiências estão contidas nos notebooks heterocedásticos. Observe que os resultados dependem fortemente da seleção de hiperparâmetro. Os gráficos abaixo mostram Log-Likelincos e RMSes no trem (cor semi-transparente) e teste (cor sólida). Círculos e barras de erro correspondem à média de validação cruzada de 10 vezes e aos desvios padrão, respectivamente.
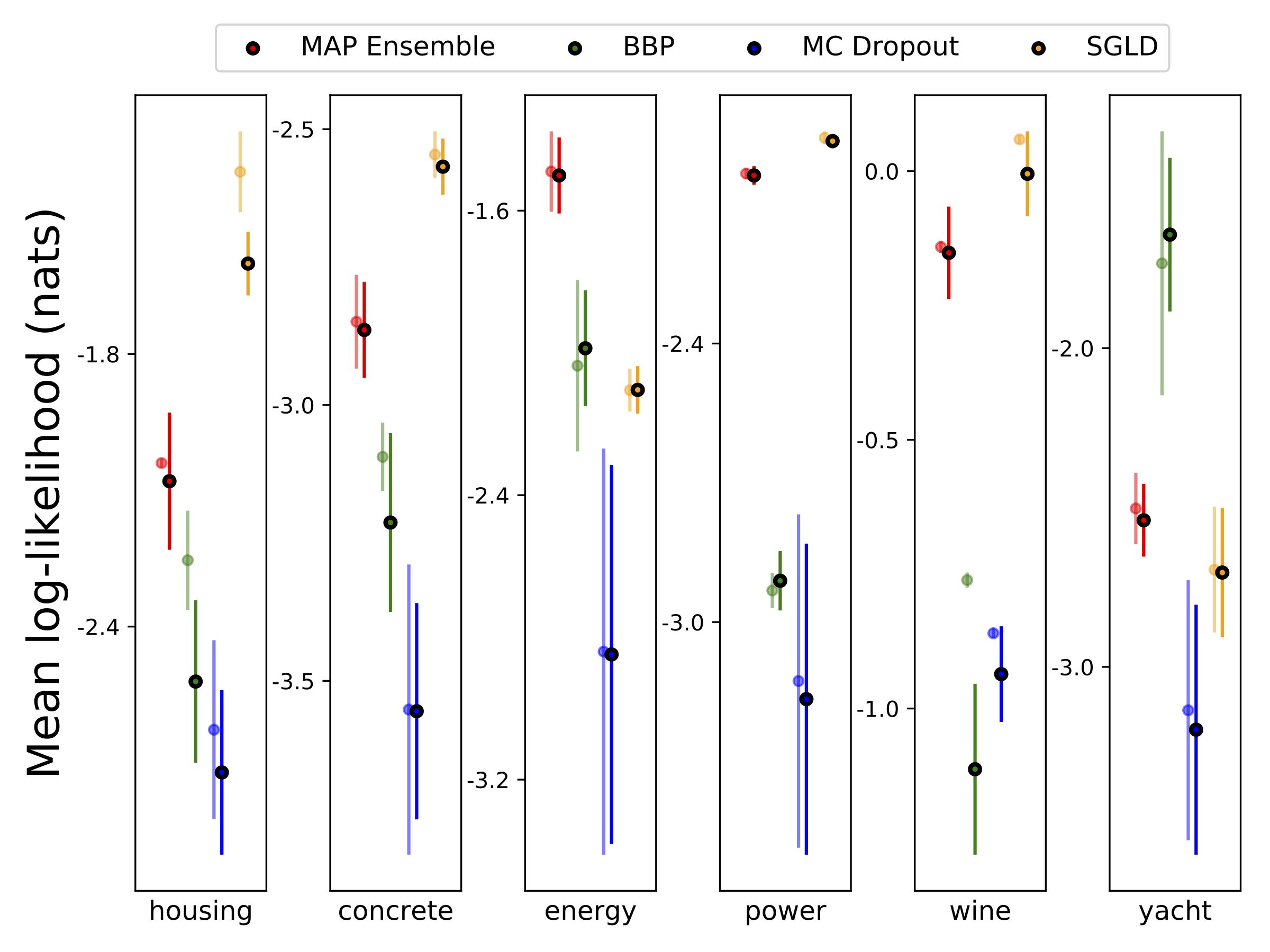
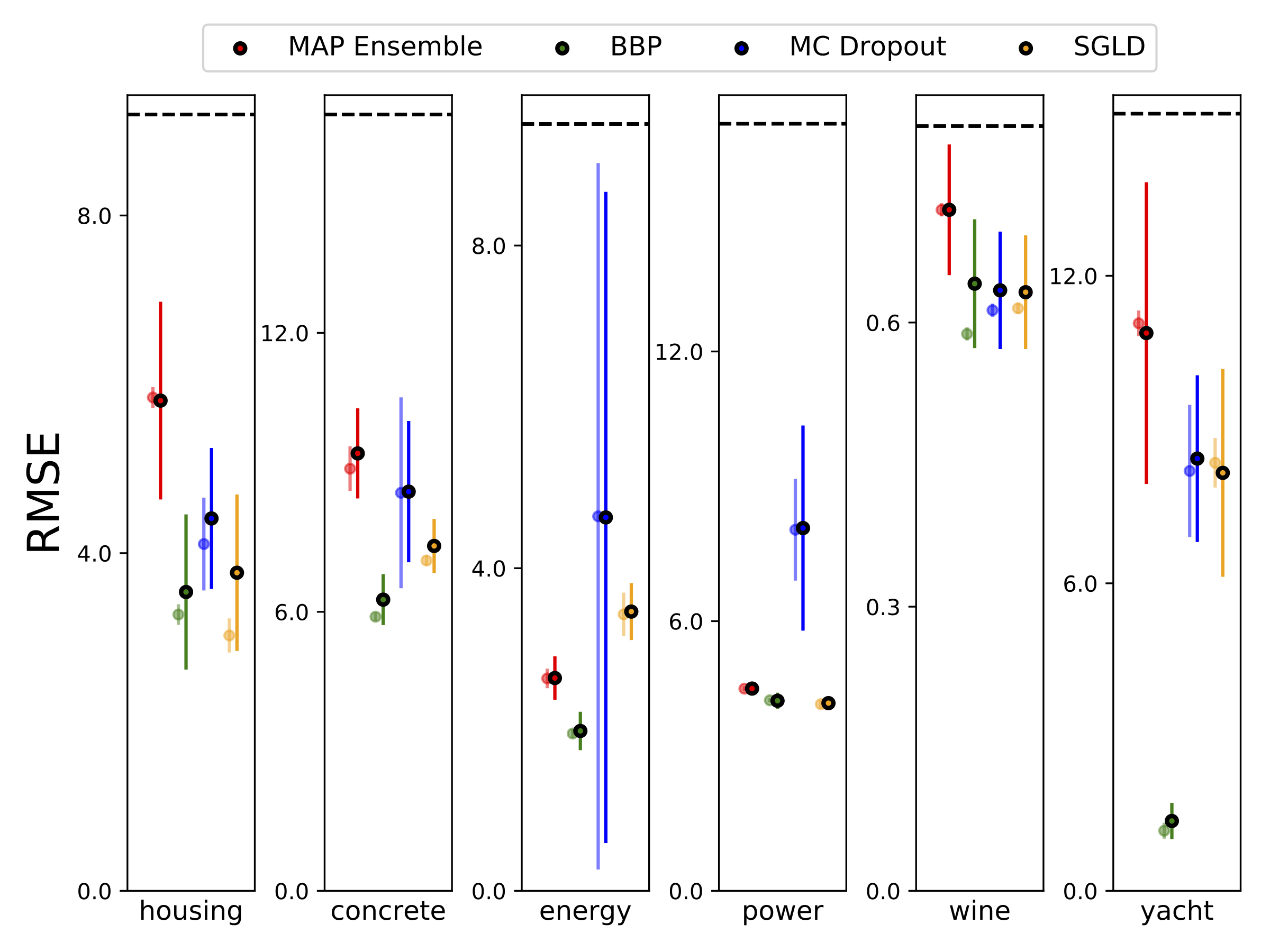
W é marginalizado com 100 amostras dos pesos para todos os modelos, exceto mapa, onde apenas um conjunto de pesos é usado.
| Teste mnist | MAPA | Ensemble de mapa | BBP Gaussian | BBP GMM | BBP Laplace | Reparam local do BBP | MC abandono | SGLD | PSGLD |
|---|---|---|---|---|---|---|---|---|---|
| Registro como | -572.9 | -496.54 | -1100.29 | -1008.28 | -892.85 | -1086.43 | -435.458 | -828.29 | -661.25 |
| Erro % | 1.58 | 1.53 | 2.60 | 2.38 | 2.28 | 2.61 | 1.37 | 1.76 | 1.76 |
Resultados do teste MNIST para métodos em consideração. O ajuste de hiperparâmetro estente não foi realizado. Nós aproximamos a distribuição preditiva posterior com 100 amostras de MC. Usamos uma rede FC com duas camadas de 1200 unidades RelU. Se não especificado, o anterior é gaussiano com std = 0,1. O P-SGLD usa o pré-condicionamento RMSPROP.
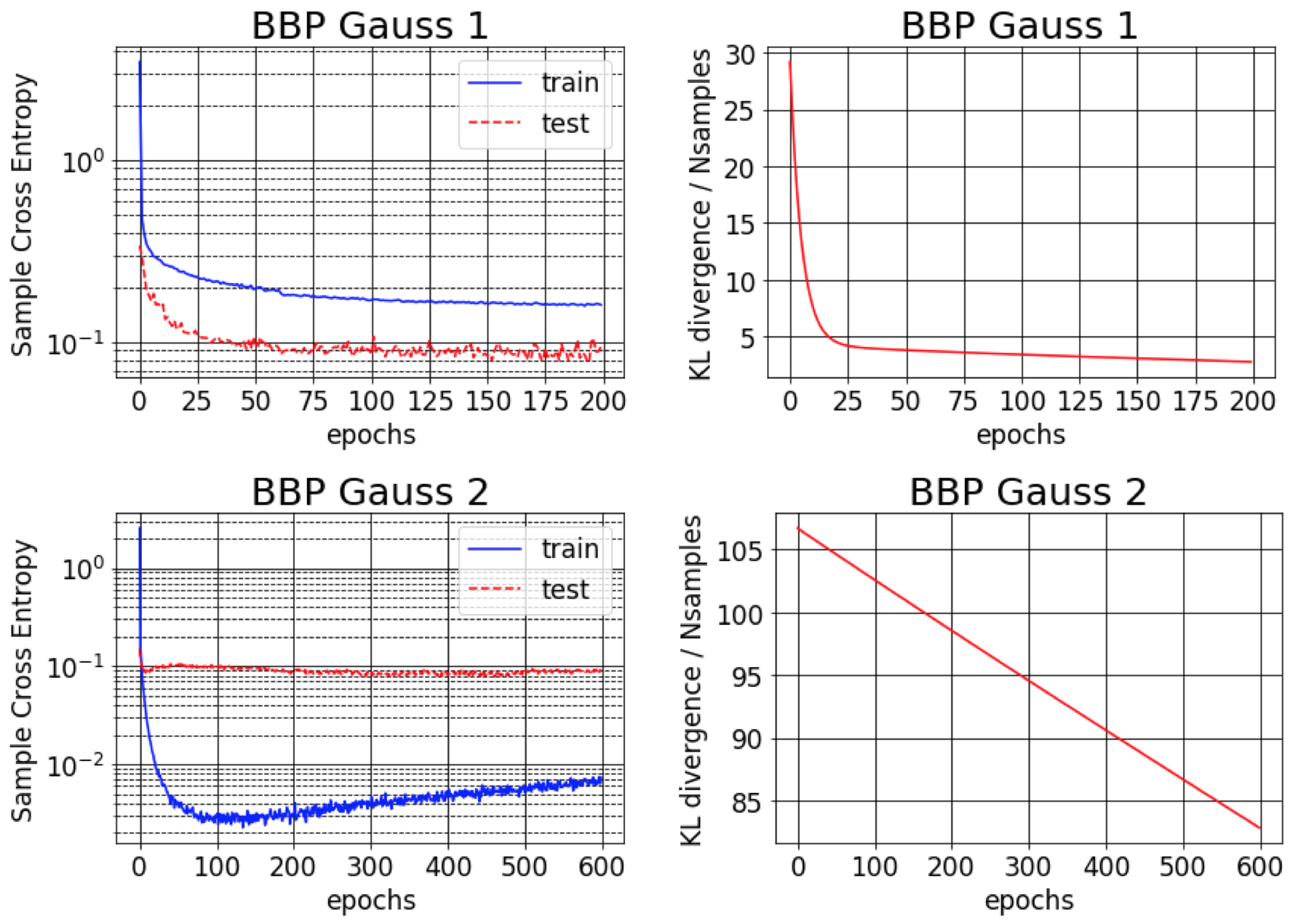
O artigo original de Bayes da BackProp relata cerca de 1% de erro no MNIST. Descobrimos que esse resultado é atingível apenas se as variações posteriores aproximadas forem inicializadas para serem muito pequenas (BBP Gauss 2). Nesse cenário, as distribuições sobre os pesos se assemelham a deltas, proporcionando um bom desempenho preditivo, mas estimativas ruins de incerteza. No entanto, ao inicializar as variações para corresponder ao anterior (BBP Gauss 1), obtemos os resultados acima. As curvas de treinamento para ambos os esquemas de configuração de hiperparâmetro são mostrados abaixo:
Incertezas totais, aleatóricas e epistêmicas obtidas ao criar amostras de Ood, aumentando o conjunto de testes do MNIST com rotações:
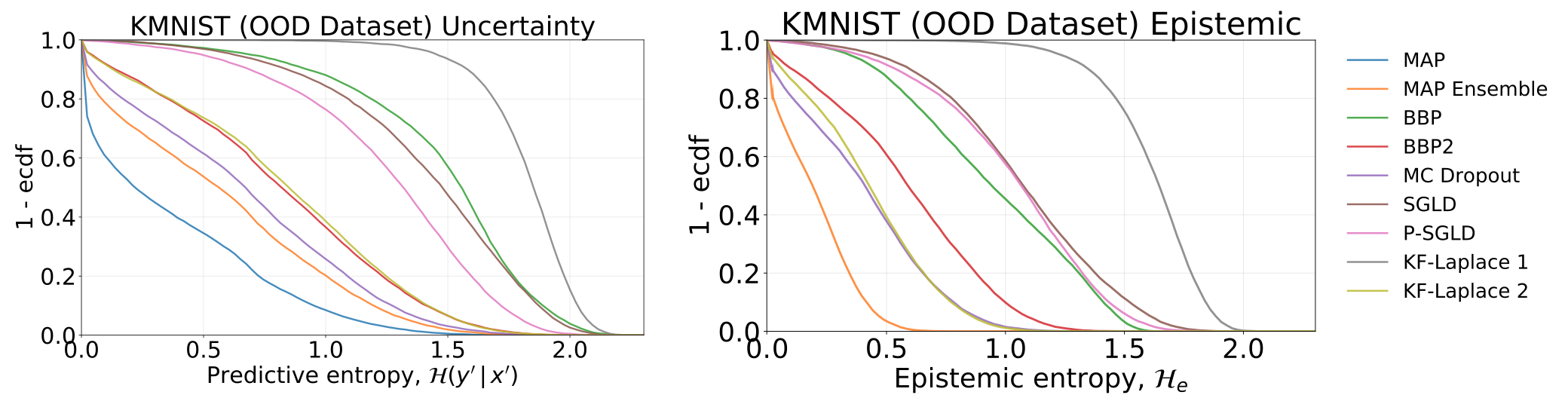
Incertezas totais e epistêmicas obtidas testando nossos modelos - que foram treinados no MNIST -, no conjunto de dados KMNIST:
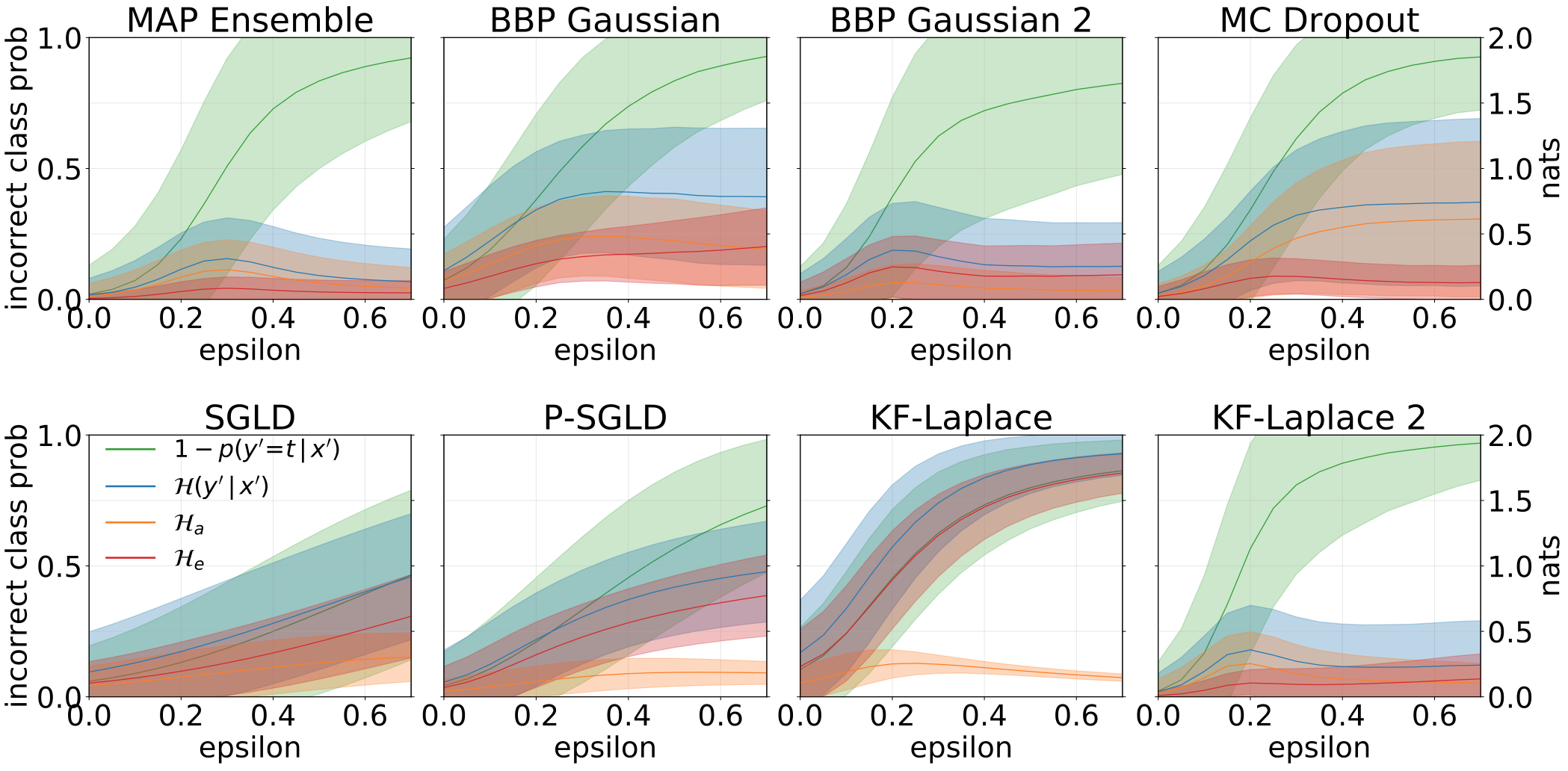
Incertezas totais, aleatóricas e epistêmicas obtidas ao alimentar nossos modelos com amostras adversárias (FGSM).
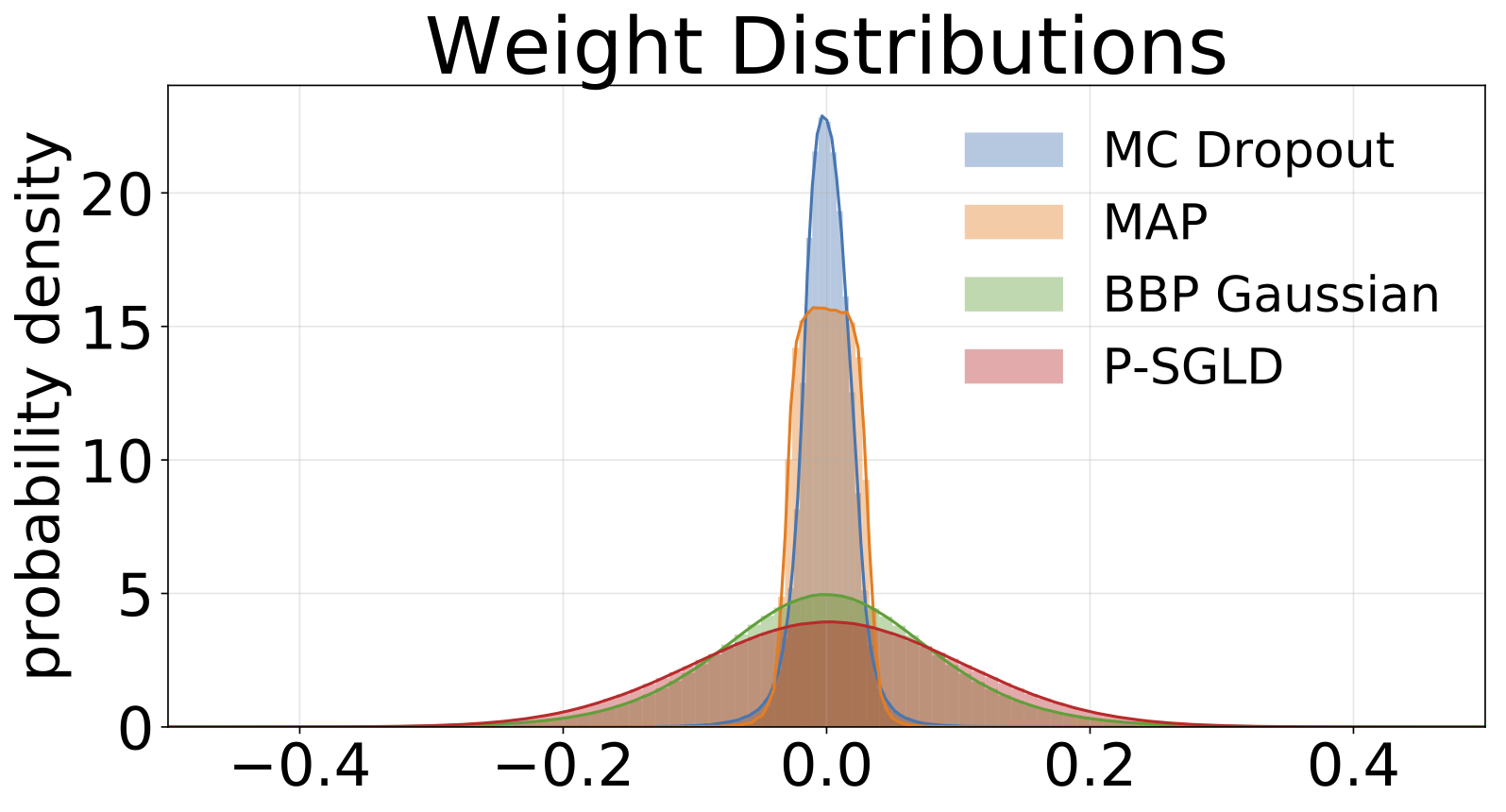
Histogramas de pesos amostrados de cada modelo treinado no MNIST. Desenhamos 10 amostras de W para cada modelo.
#PENDÊNCIA