تطبيقات Pytorch لطرق الاستدلال التقريبية التالية:
نقدم أيضًا رمزًا لـ:
تم كتابة المشروع في Python 2.7 و Pytorch 1.0.1. إذا كان CUDA متاحًا ، فسيتم استخدامه تلقائيًا. يمكن أن تعمل النماذج أيضًا على وحدة المعالجة المركزية لأنها ليست كبيرة بشكل مفرط.
لقد أجرينا تجارب الانحدار متماثلين ومتجانسة على مجموعات بيانات الألعاب ، التي تم إنشاؤها باستخدام (Gaussian Process Ground Truth) ، وكذلك على البيانات الحقيقية (ست مجموعات بيانات UCI).
دفاتر/تصنيف/(اسم نموذج) _ (التجربة) .IpyNB : يحتوي على تجارب باستخدام (نموذج) على (التجربة) ، أي محلية متجانسة/غير متجانسة. تحتوي دفاتر الملاحظات غير المتجانسة على كل من تجارب مجموعة بيانات Toy و UCI لـ A (ModelName).
نحن نقدم أيضًا أجهزة الكمبيوتر المحمولة Google Colab. هذا يعني أنه يمكنك الجري على وحدة معالجة الرسومات (مجانًا!). لا توجد تعديلات مطلوبة -تتم إضافة جميع التبعيات ومجموعات البيانات من داخل دفاتر الملاحظات -باستثناء تحديد وقت التشغيل -> تغيير نوع وقت التشغيل -> Accelerator Hardware -> GPU.
Train_ (ModelName) _ (DataSet) .py : Trains (ModelName) على (DataSet). سيتم حفظ مقاييس التدريب والأوزان النموذجية إلى الدلائل المحددة.
SRC/ : المرافق العامة وتعريفات النموذج.
دفاتر/تصنيف : مجموعة من أجهزة الكمبيوتر المحمولة التي تسمح بتدريب وتقييم وتشغيل تجارب عدم اليقين في دوران الأرقام. كما أنها تسمح بتخطيط توزيع الوزن وتشذيب الوزن. أنها تسمح بتحميل النماذج التي تم تدريبها مسبقًا للتجربة.
(https://arxiv.org/abs/1505.05424)
دفاتر كولاب مع نماذج الانحدار: BBP محدود متماثل / غير متجانسة
تدريب نموذج على Mnist:
python train_BayesByBackprop_MNIST.py [--model [MODEL]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]للحصول على شرح لحجج البرنامج النصي:
python train_BayesByBackprop_MNIST.py -hيتم الحصول على أفضل النتائج مع لابلاس قبل.
(https://arxiv.org/abs/1506.02557)
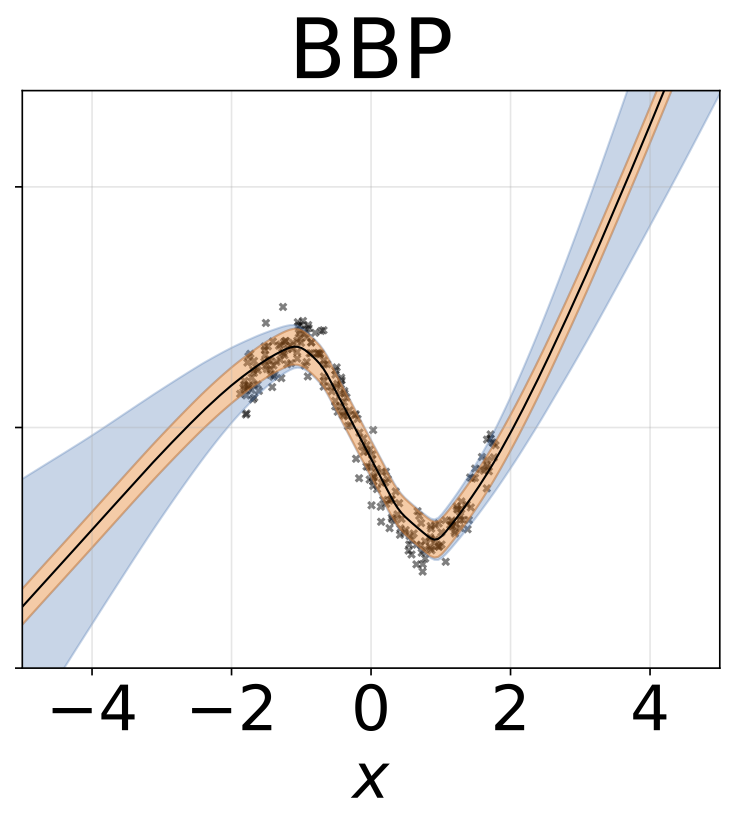
بايز عن طريق الاستدلال الخلفي حيث يتم حساب متوسط وتباين التنشيط في شكل مغلق. يتم أخذ عينات من التنشيط بدلا من الأوزان. هذا يجعل تباين مقياس مقدر مونت كارلو إلبو كـ 1/م ، حيث يكون M هو حجم الحصرة. عينة أوزان المقاييس (M-1)/م. يمكن أيضًا حساب اختلاف KL بين Gaussians في شكل مغلق ، مما يقلل من التباين. حساب كل عصر أسرع وكذلك التقارب.
تدريب نموذج على Mnist:
python train_BayesByBackprop_MNIST.py --model Local_Reparam [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]](https://arxiv.org/abs/1506.02142)
تم تعيين معدل تسرب ثابت قدره 0.5.
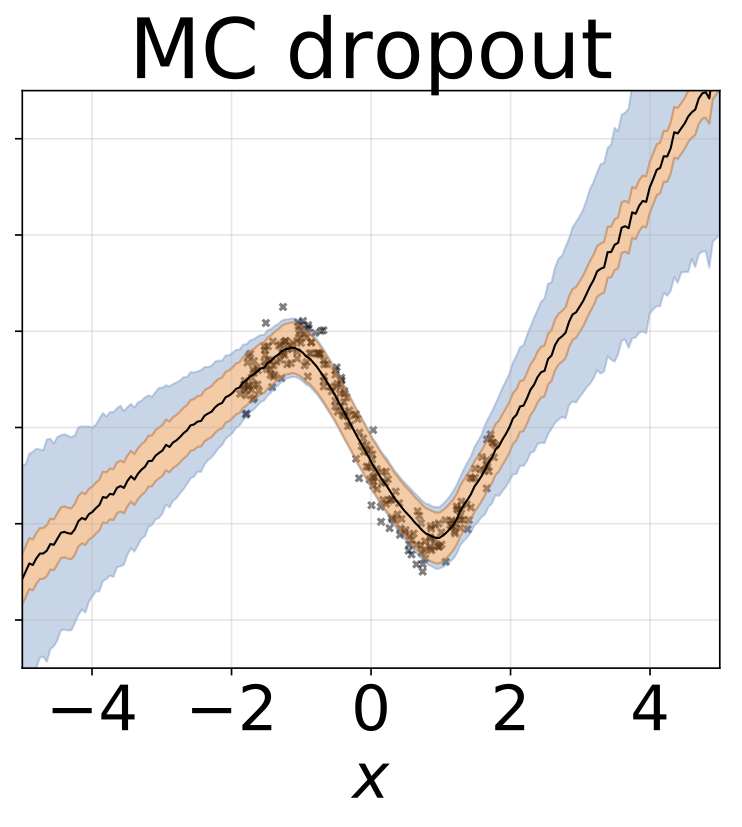
دفاتر كولاب مع نماذج الانحدار: MC المتسرب متجانسة متجانسة متجانسة
تدريب نموذج على Mnist:
python train_MCDropout_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]للحصول على شرح لحجج البرنامج النصي:
python train_MCDropout_MNIST.py -h(https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf)
من أجل التقارب مع الخلفي الحقيقي على W ، يجب أن يتم تلبيس معدل التعلم وفقًا لظروف روبنز مونرو. في الممارسة العملية ، نستخدم معدل التعلم الثابت.
دفاتر كولاب مع نماذج الانحدار: SGLD متماثلين / متغايرة متجانسة
تدريب نموذج على Mnist:
python train_SGLD_MNIST.py [--use_preconditioning [USE_PRECONDITIONING]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]للحصول على شرح لحجج البرنامج النصي:
python train_SGLD_MNIST.py -h(https://arxiv.org/abs/1512.07666)
SGLD مع الشروط المسبقة RMSPROP. يجب استخدام معدل التعليم العالي من الفانيليا SGLD.
تدريب نموذج على Mnist:
python train_SGLD_MNIST.py --use_preconditioning True [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]يتم تدريب شبكات متعددة على عينات فرعية من مجموعة البيانات.
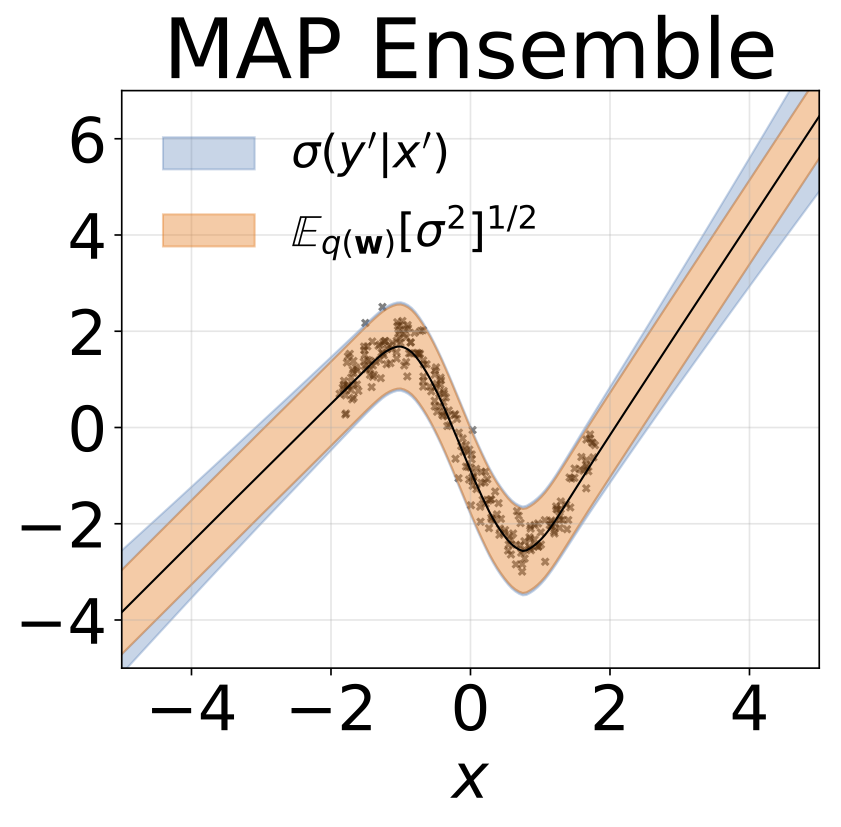
دفاتر كولاب مع نماذج الانحدار: MAP ENSEMBEL
تدريب مجموعة على Mnist:
python train_Bootrap_Ensemble_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--subsample [SUBSAMPLE]] [--n_nets [N_NETS]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]للحصول على شرح لحجج البرنامج النصي:
python train_Bootrap_Ensemble_MNIST.py -h(https://openreview.net/pdf؟id=skdvd2xaz)
قم بتدريب شبكة الخريطة ثم حساب سلسلة Taylor Series من الدرجة الثانية على الانحناء حول وضع الخلفي. يتم استخدام تقريب الهيسيان القطري ، حيث يتم حساب التبعيات داخل الطبقة فقط. يتم تقريب Hessian كمنتج Kronecker لتوقع عوامل Hessian الخاصة بوجود بيانات واحدة. تقريب Hessian يمكن أن يستغرق بعض الوقت. لحسن الحظ ، يجب القيام به مرة واحدة فقط.
تدريب شبكة خريطة على Mnist و Hessian التقريبي:
python train_KFLaplace_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--hessian_diag_sig [HESSIAN_DIAG_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]للحصول على شرح لحجج البرنامج النصي:
python train_KFLaplace_MNIST.py -hلاحظ أننا نوفر العوامل الهسانية غير المقيدة وغير المقيدة. سيسمح ذلك بإجراء تغييرات رخيصة حسابية على وقت الاستدلال السابق لأن Hessian لن يحتاج إلى إعادة حساب. سوف يتطلب الاستدلال قلب العوامل الهسوية التقريبية وأخذ العينات من التوزيع الطبيعي المصفوفة. يظهر هذا في دفاتر الملاحظات/KFAC_LAPLACE_MNIST.IPYNB
(https://arxiv.org/abs/1402.4102)
نقوم بتنفيذ النسخة التي تم تكييفها من هذه الخوارزمية ، المقترحة هنا للعثور على فرط البارامترات تلقائيًا أثناء الاحتراق. نحن نضع غاوسي سابقة على أوزان الشبكة وفرط غاما على دقة غاوسي.
قم بتشغيل SG-HMC-SA حرق وأخذ عينات ، وتوفير الأوزان في ملف محدد.
python train_SGHMC_MNIST.py [--epochs [EPOCHS]] [--sample_freq [SAMPLE_FREQ]] [--burn_in [BURN_IN]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]للحصول على شرح لحجج البرنامج النصي:
python train_SGHMC_MNIST.py -hيوفر استنتاج الخريطة تقديرًا لقيم المعلمة. عندما يتم توفيرها مع مدخلات التوزيع ، مثل الأرقام المدورة ، فإن هذه النماذج ثم تنبؤات خاطئة بثقة عالية.
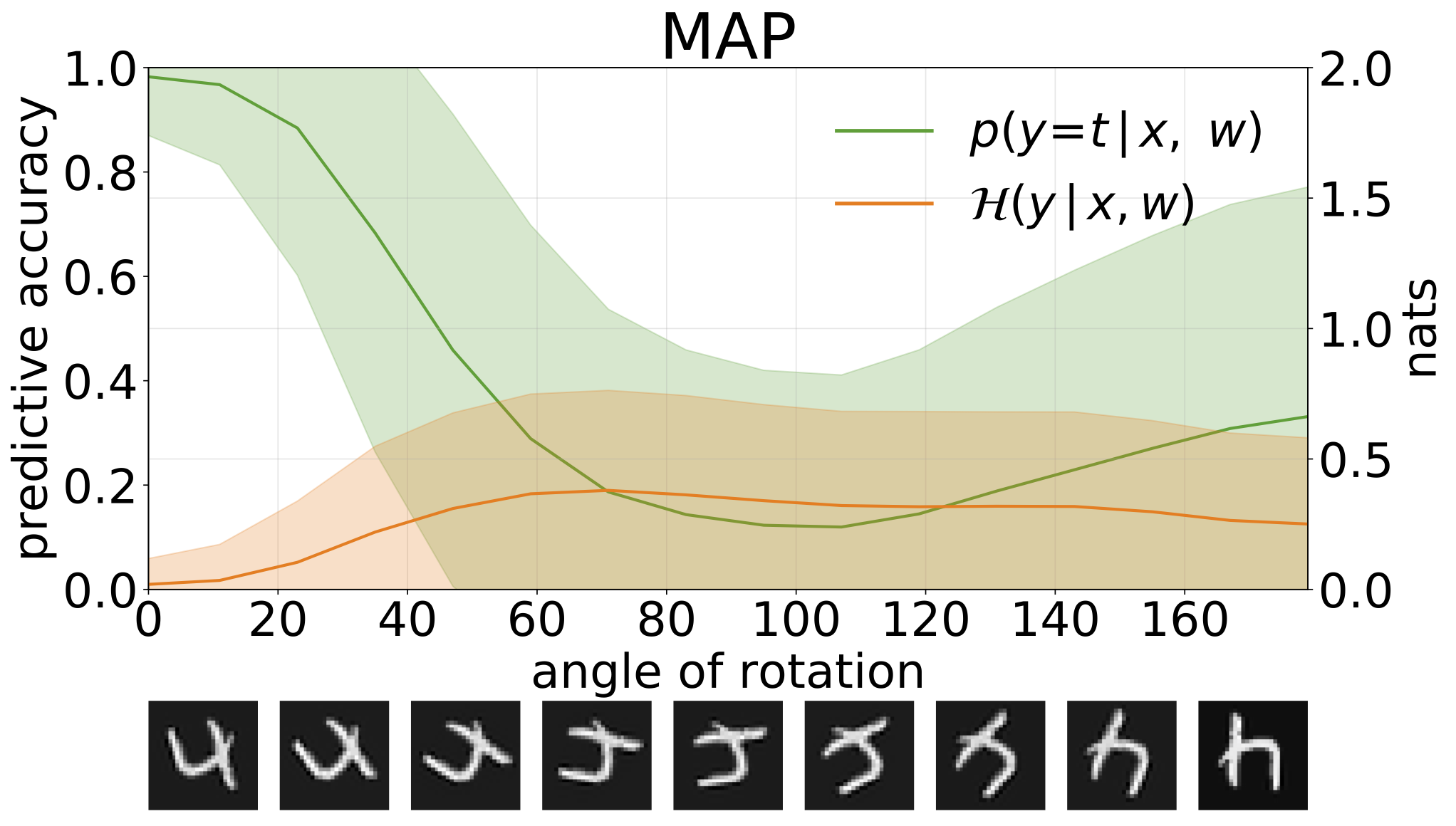
يمكننا قياس عدم اليقين في تنبؤات نماذجنا من خلال الانتروبيا التنبؤية. يمكننا أن نتحلل هذا المصطلح من أجل التمييز بين نوعين من عدم اليقين. يمكن قياس عدم اليقين الناجم عن الضوضاء في البيانات ، أو عدم اليقين aleatoric ، على أنها الانتروبيا المتوقعة للتنبؤات النموذجية. يمكن قياس عدم اليقين النموذج أو عدم اليقين المعرفي كفرق بين الانتروبيا الكلية والإنتروبيا aleatoric.
لعبة الانحدار متماثل التماثيل. يتم إنشاء البيانات بواسطة GP مع kernel RBF (L = 1 ، σn = 0.3). نستخدم شبكة FC واحدة من طراز Onterput مع طبقة مخفية واحدة من 200 وحدة RELU للتنبؤ بمعنى الانحدار μ (x). يتم تعلم سجل ثابت σ بشكل منفصل.
نفس السيناريو مثل القسم السابق ولكن السجل σ (x) يتم التنبؤ به من المدخلات.
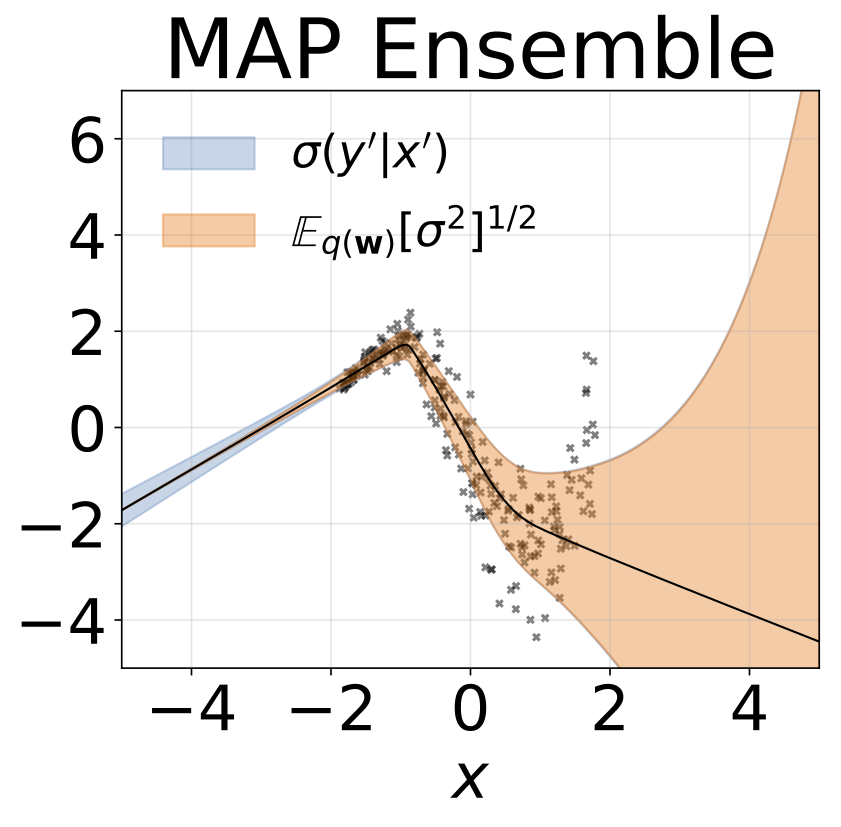
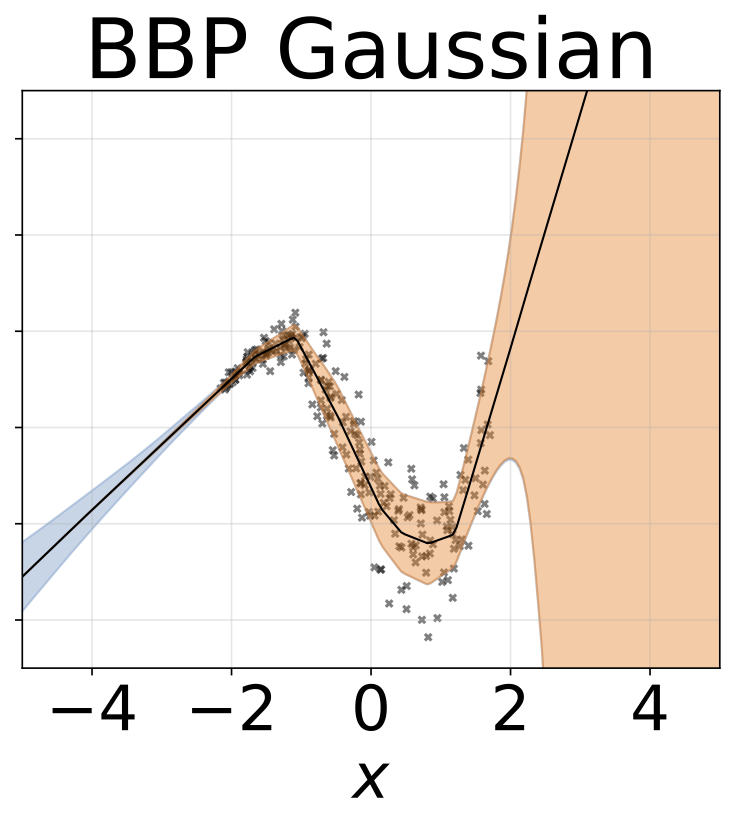
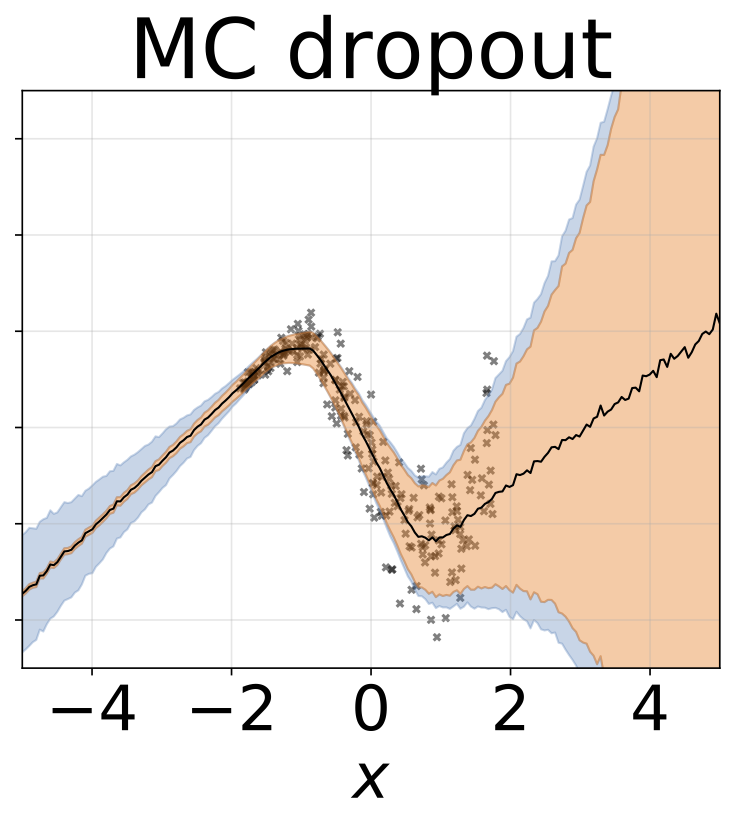
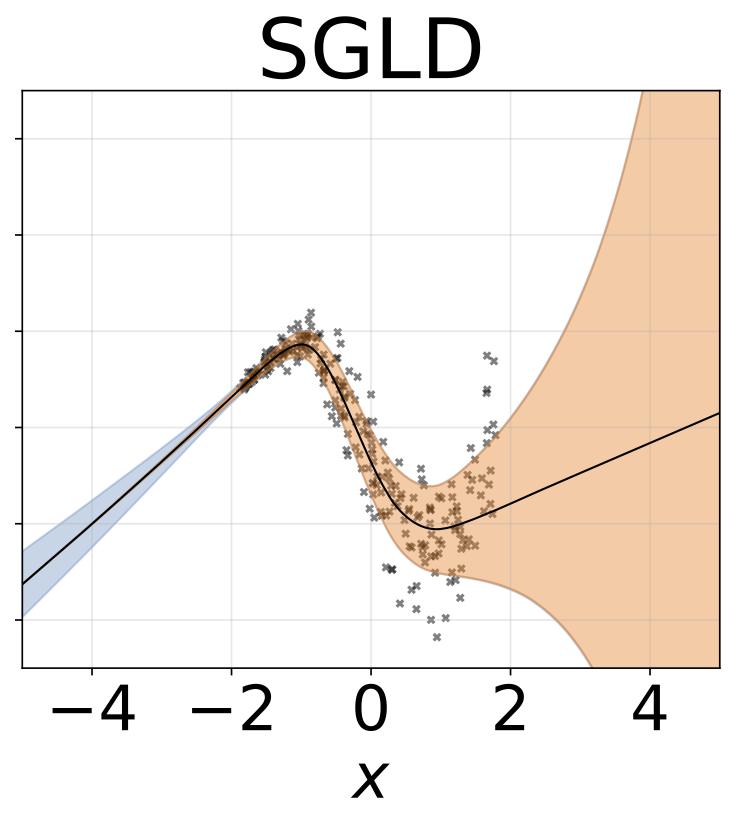
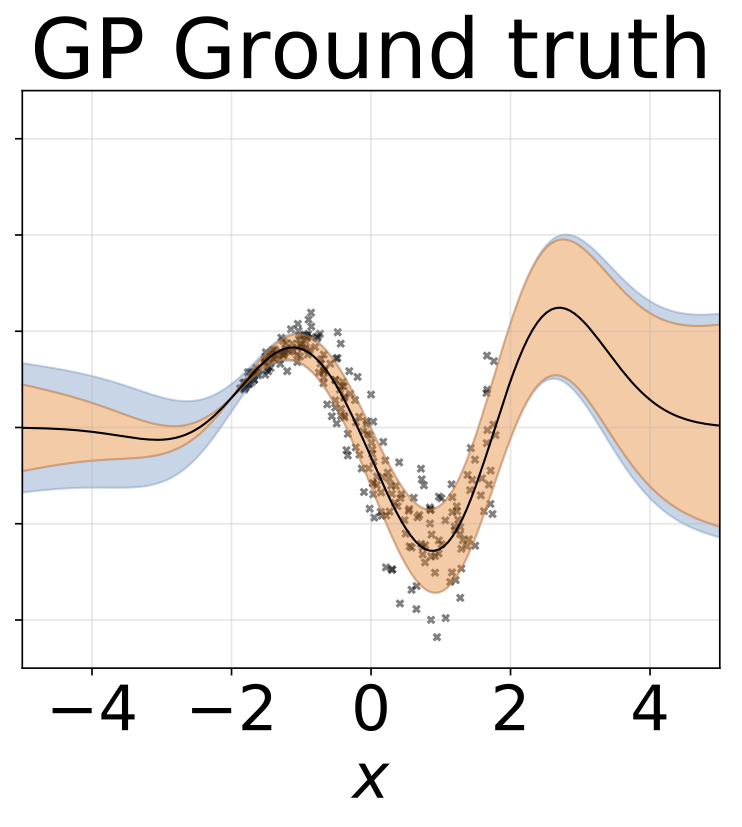
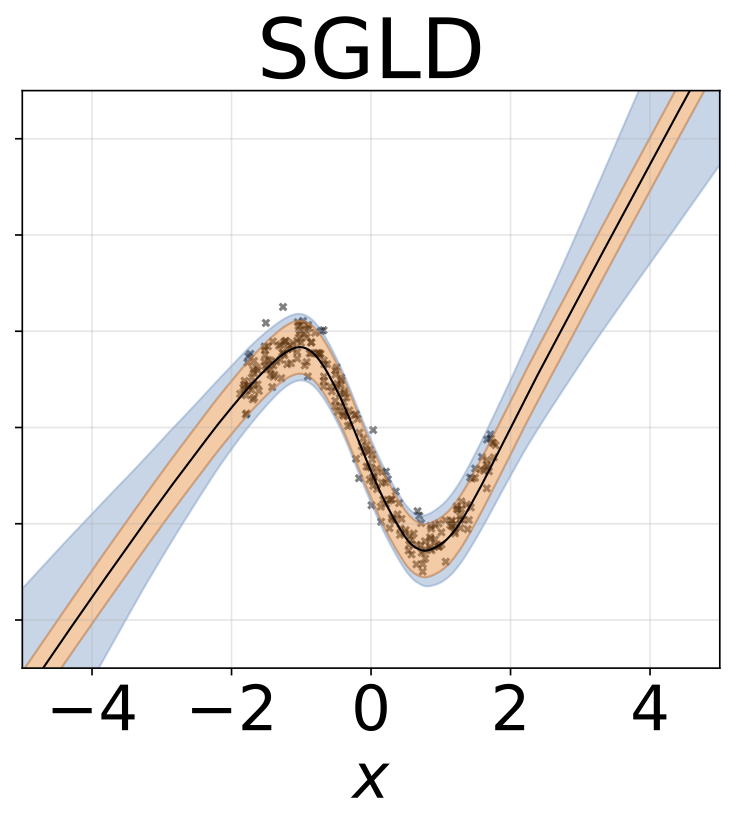
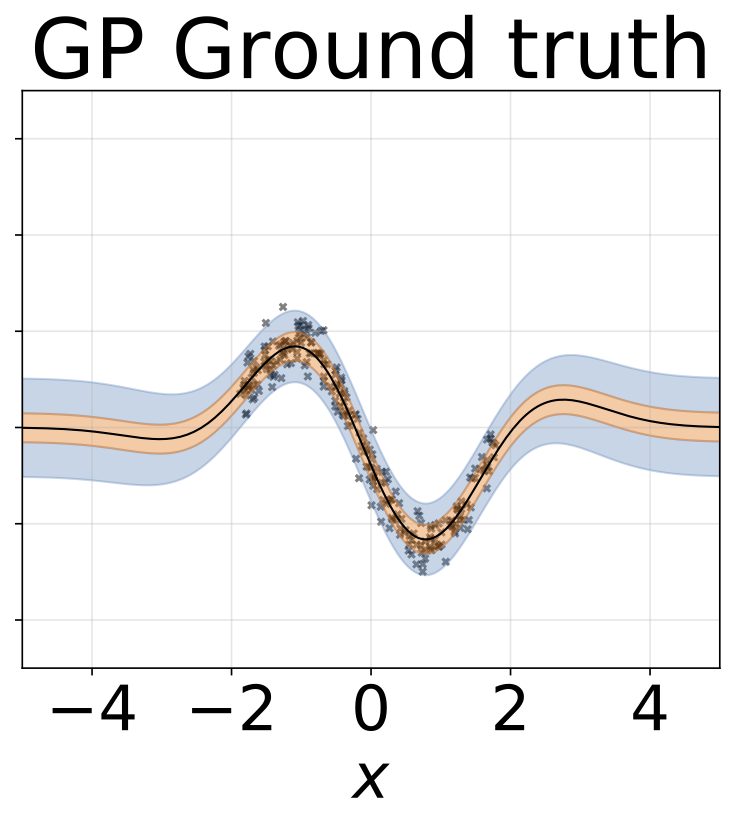
مهمة الانحدار متغاير التغاير. يتم إنشاء البيانات بواسطة GP مع kernel RBF (L = 1 σn = 0.3 · | x + 2 |). نحن نستخدم شبكة ثنائية الرؤوس مع 200 وحدة RELU للتنبؤ بمعدل الانحدار μ (x) وسجل الانحراف القياسي السجل σ (x).
أجرينا الانحدار غير المتجانس على مجموعات بيانات UCI الست (الإسكان ، والخرسانة ، وكفاءة الطاقة ، ومحطات الطاقة ، والنبيذ الأحمر واليخت) ، باستخدام التحقق من صحة 10-Foild. كل هذه التجارب موجودة في دفاتر الملاحظات غير المتجانسة. لاحظ أن النتائج تعتمد اعتمادًا كبيرًا على اختيار فرط البارامتر. تظهر المؤامرات أدناه احتمالات تسجيل الدخول و RMSEs على القطار (لون شبه شفاف) واختبار (لون صلب). تتوافق الدوائر وأشرطة الخطأ مع متوسط التحقق من صحة 10 أضعاف والانحرافات المعيارية على التوالي.
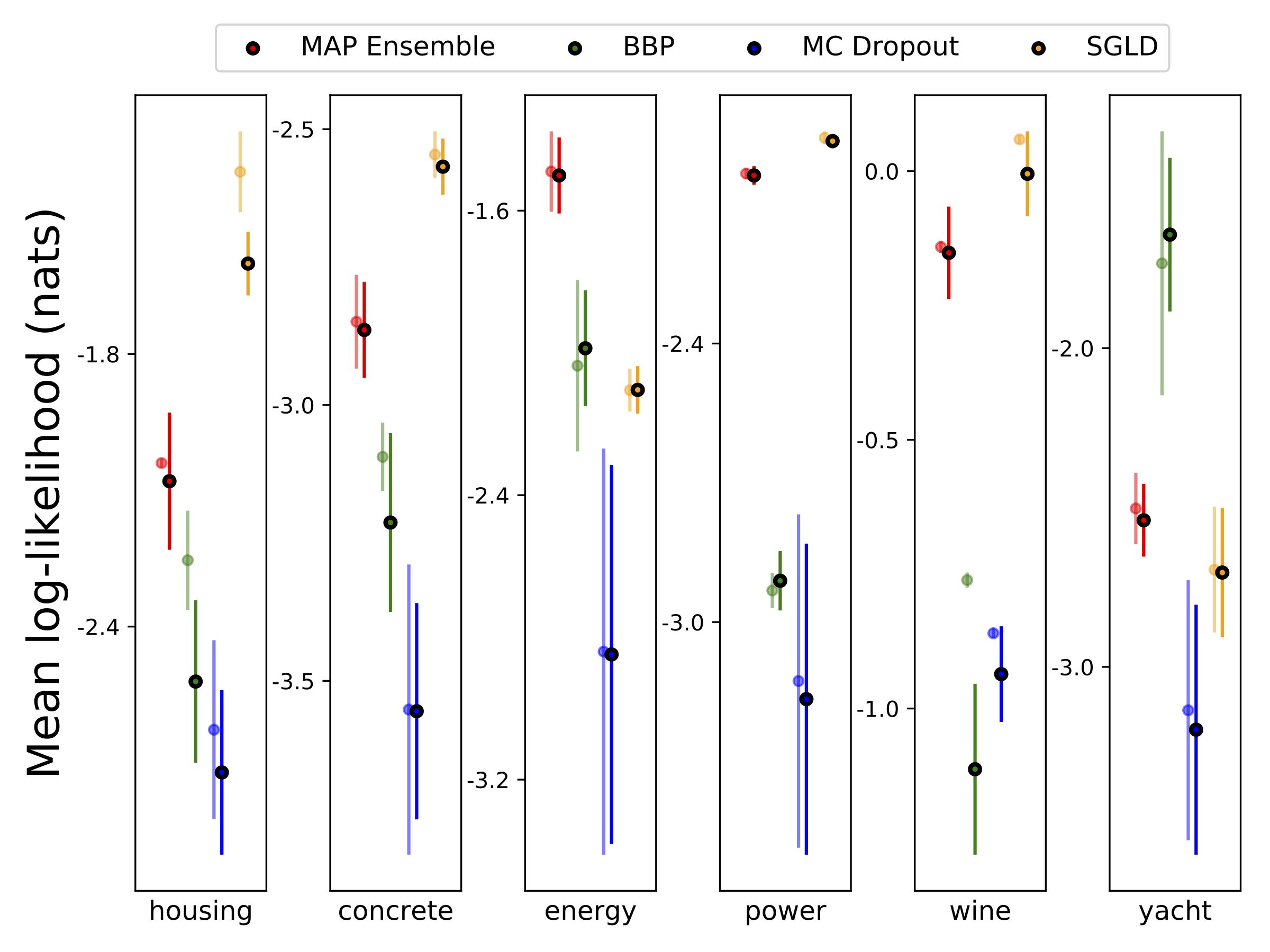
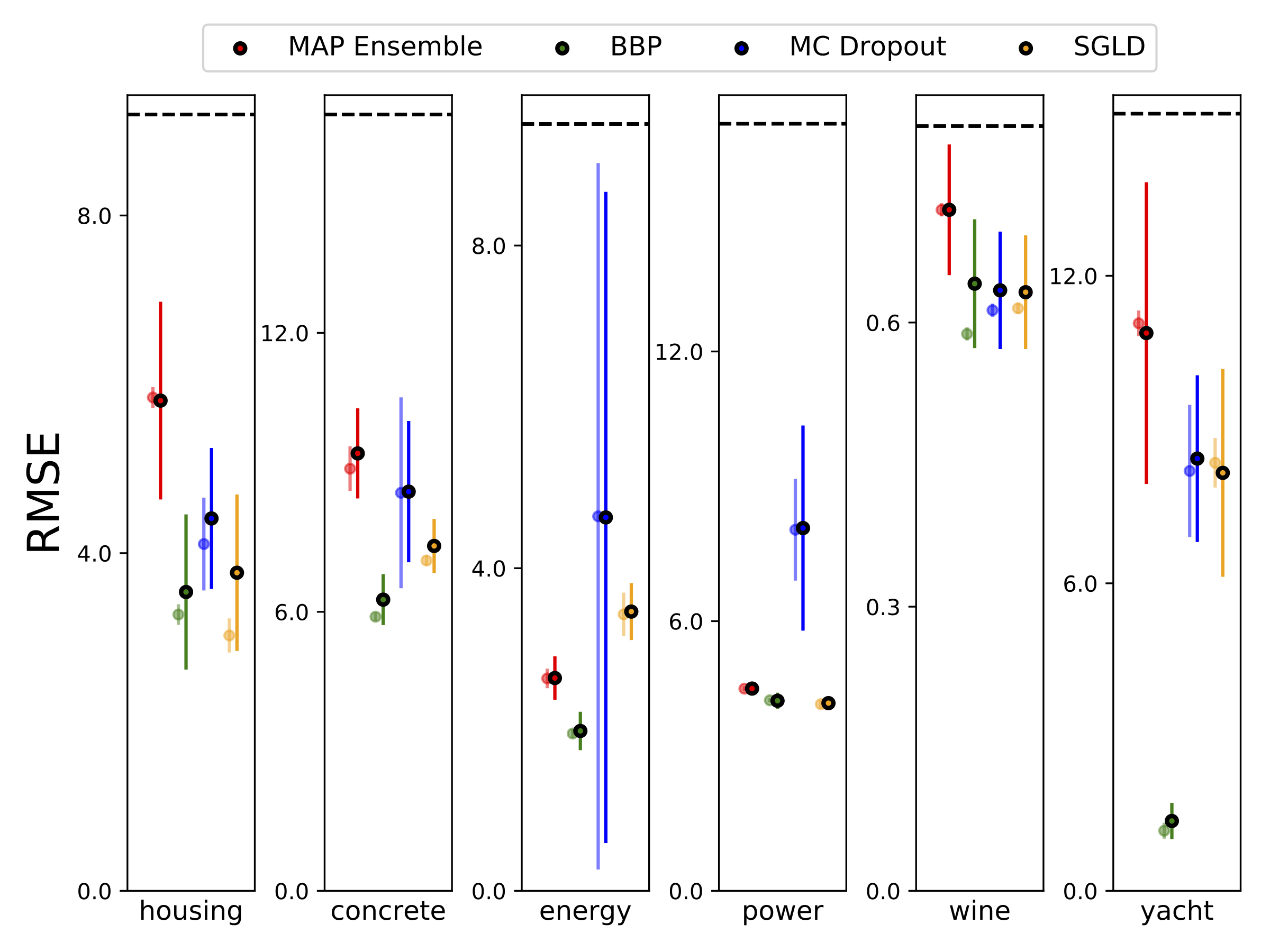
يتم تهميش W مع 100 عينة من الأوزان لجميع النماذج باستثناء الخريطة ، حيث يتم استخدام مجموعة واحدة فقط من الأوزان.
| اختبار mnist | رسم خريطة | خريطة فرقة | BBP Gaussian | BBP GMM | BBP لابلاس | BBP المحلي reparam | MC التسرب | SGLD | PSGLD |
|---|---|---|---|---|---|---|---|---|---|
| سجل مثل | -572.9 | -496.54 | -1100.29 | -1008.28 | -892.85 | -1086.43 | -435.458 | -828.29 | -661.25 |
| خطأ ٪ | 1.58 | 1.53 | 2.60 | 2.38 | 2.28 | 2.61 | 1.37 | 1.76 | 1.76 |
نتائج اختبار MNIST للطرق قيد النظر. لم يتم تنفيذ التنفق Hyperparameter. نحن نقرب التوزيع التنبئي الخلفي مع 100 عينة MC. نستخدم شبكة FC مع طبقتين من 1200 وحدة RELU. إذا كان غير محدد ، فإن السابق هو gaussian مع الأمراض المنقولة جنسيا = 0.1. يستخدم P-SGLD الشروح المسبقة RMSPROP.
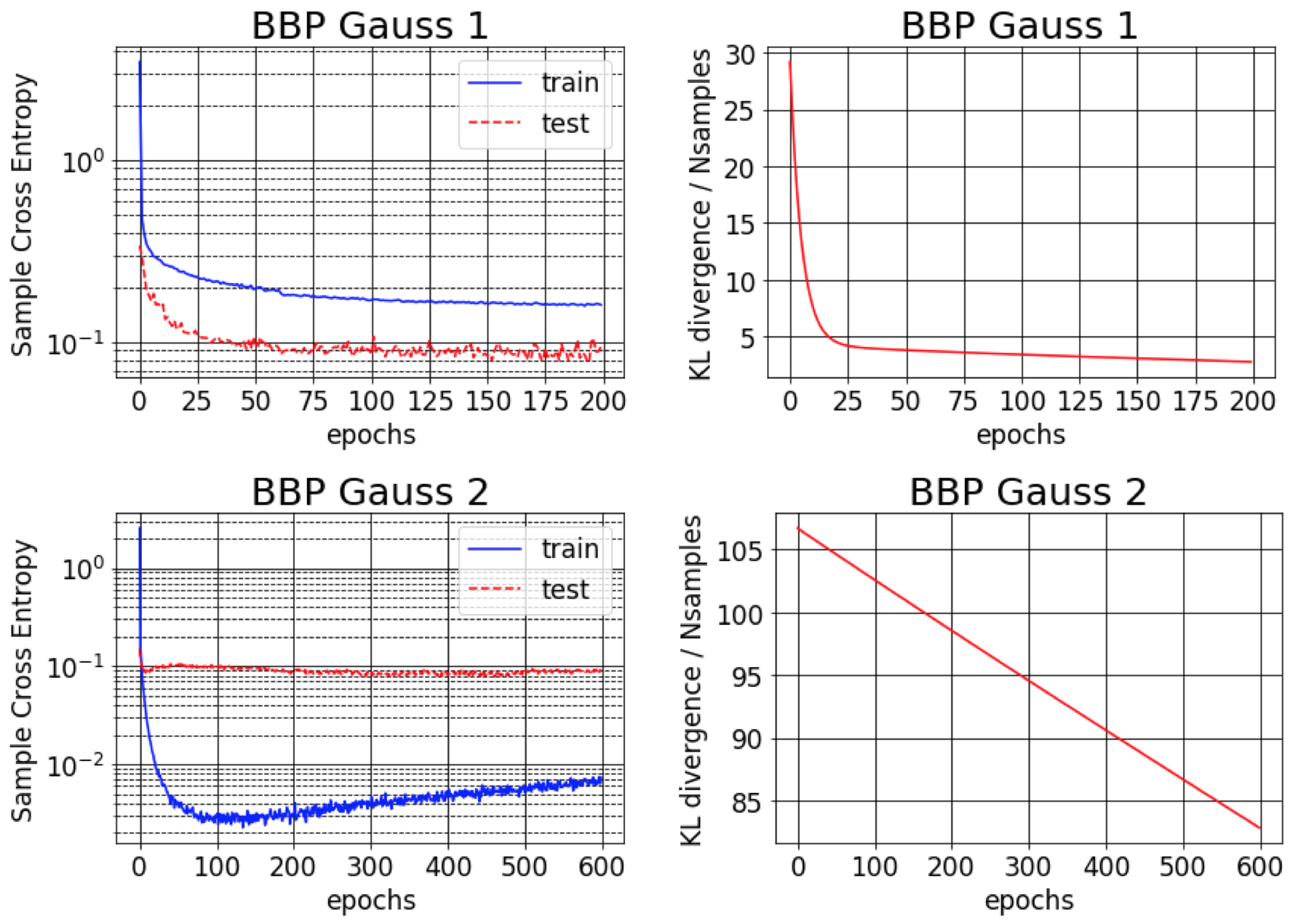
الورقة الأصلية لـ Bayes بواسطة Backprop تقارير حوالي 1 ٪ خطأ على MNIST. نجد أن هذه النتيجة لا يمكن تحقيقها إلا إذا تم تهيئة التباينات الخلفية التقريبية لتكون صغيرة جدًا (BBP Gauss 2). في هذا السيناريو ، تشبه التوزيعات على الأوزان الدلتا ، مما يعطي أداء تنبؤي جيد ولكن تقديرات عدم اليقين السيئة. ومع ذلك ، عند تهيئة التباينات لتتناسب مع السابق (BBP Gauss 1) ، نحصل على النتائج المذكورة أعلاه. فيما يلي منحنيات التدريب لكلا من مخططات التكوين المفرطة المفرطة:
إجمالي حالات عدم اليقين المعرفية والمعرفية التي تم الحصول عليها عند إنشاء عينات OOD عن طريق زيادة اختبار MNIST مع الدورات:
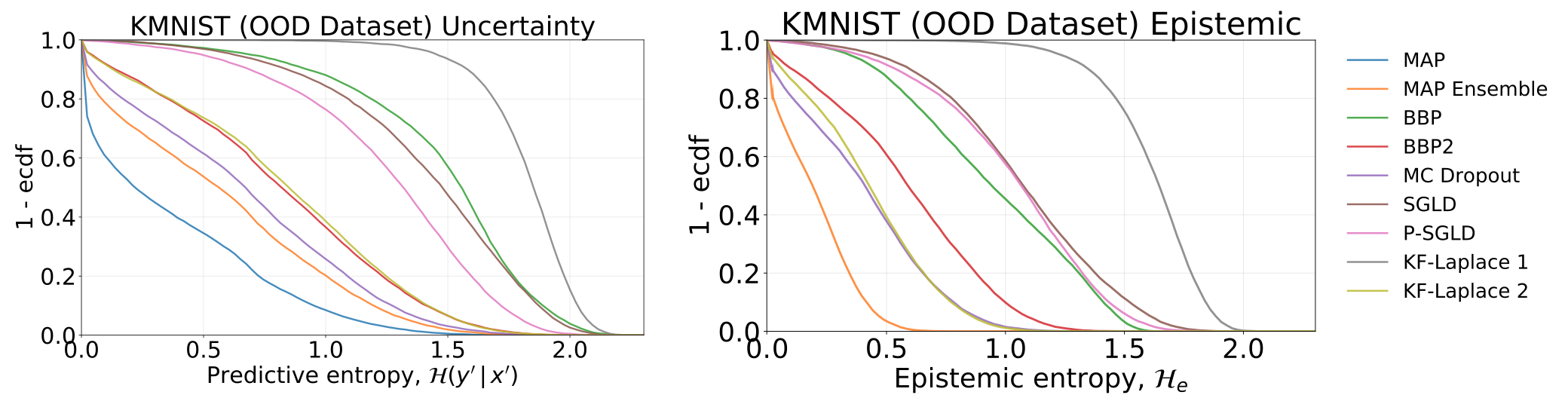
أوجه عدم اليقين الكلية والمعرفية التي تم الحصول عليها عن طريق اختبار نماذجنا ، والتي تم تدريبها على MNIST - على مجموعة بيانات KMNIST:
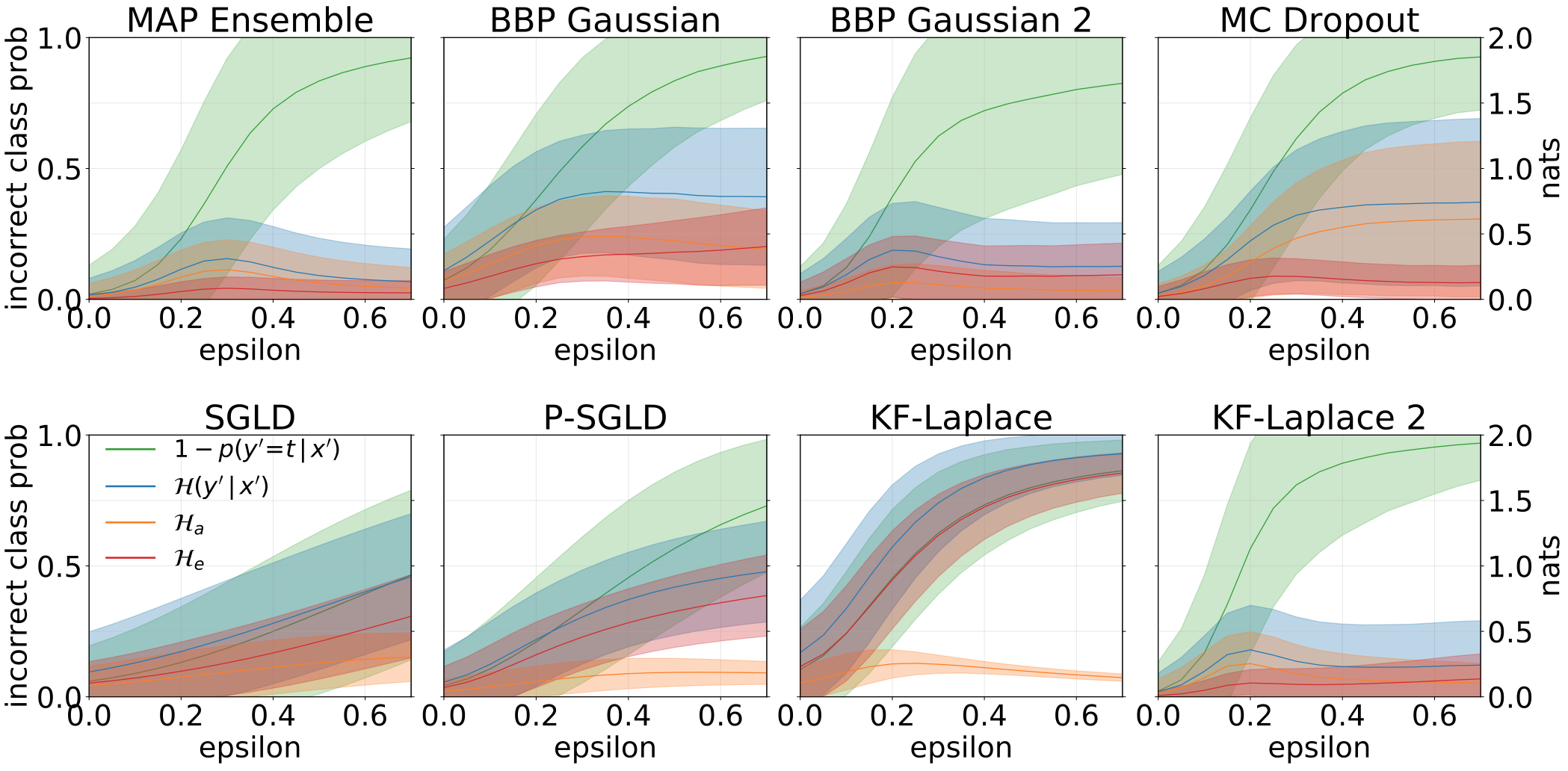
الكلي ، عدم اليقين aleatoric و exhiptemy التي تم الحصول عليها عند تغذية نماذجنا بعينات عدوانية (FGSM).
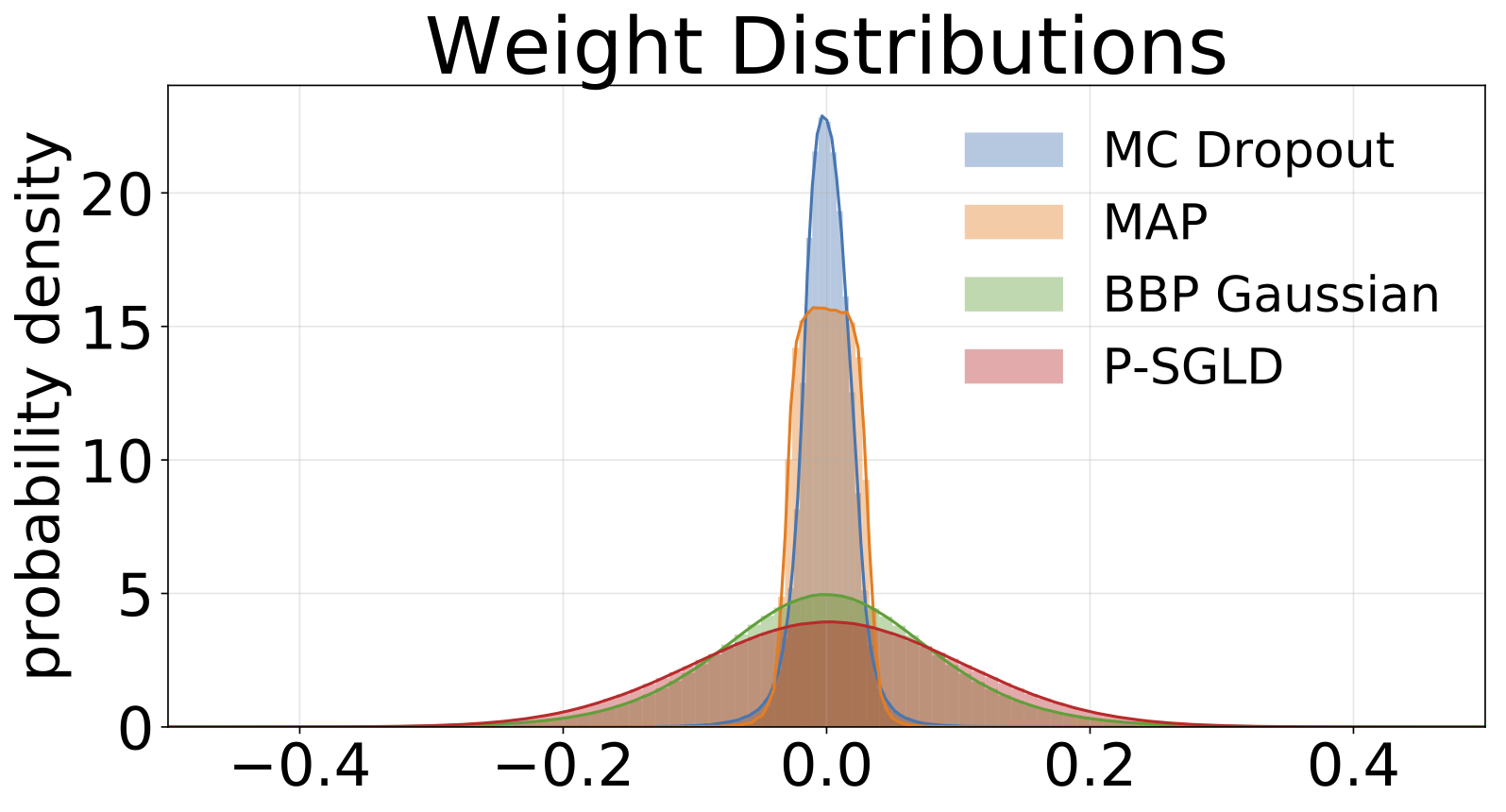
الرسوم البيانية للأوزان التي تم أخذ عينات منها من كل نموذج مدرب على MNIST. نرسم 10 عينات من W لكل نموذج.
#Todo