Implémentations de Pytorch pour les méthodes d'inférence approximatives suivantes:
Nous fournissons également du code pour:
Le projet est écrit dans Python 2.7 et Pytorch 1.0.1. Si CUDA est disponible, il sera utilisé automatiquement. Les modèles peuvent également fonctionner sur CPU car ils ne sont pas excessivement grands.
Nous avons réalisé des expériences de régression homoscédastique et hétéroscédastique sur les ensembles de données de jouets, générés avec (Gaussien Process Ground Truth), ainsi que sur les données réelles (six ensembles de données UCI).
Notes de carnet / classification / (ModelName) _ (expérimentType) .Ipynb : contient des expériences utilisant (ModelName) sur (expérimentalype), c'est-à-dire homoscédastique / hétéroscédastique. Les ordinateurs portables hétéroscédastiques contiennent des expériences de jeu de données Toy et UCI pour une donnée (nom ModelN).
Nous fournissons également des cahiers Google Colab. Cela signifie que vous pouvez courir sur un GPU (gratuitement!). Aucune modification requise - toutes les dépendances et ensembles de données sont ajoutés à partir des ordinateurs portables - sauf pour la sélection de l'exécution -> Modifier le type d'exécution -> Accélérateur matériel -> GPU.
Train_ (ModelName) _ (ensemble de données) .py : trains (ModelName) sur (ensemble de données). Les mesures de formation et les poids du modèle seront enregistrées dans les répertoires spécifiés.
SRC / : Utilitaires généraux et définitions de modèle.
Cahiers / classification : un asort de cahiers qui permettent la formation, l'évaluation et le fonctionnement des expériences d'incertitude de rotation des chiffres. Ils permettent également le traçage de distribution de poids et l'élagage du poids. Ils permettent le chargement de modèles pré-formés pour l'expérimentation.
(https://arxiv.org/abs/1505.05424)
Cahiers de colab avec modèles de régression: bbp homoscédastique / hétéroscédastique
Former un modèle sur MNIST:
python train_BayesByBackprop_MNIST.py [--model [MODEL]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Pour une explication des arguments du script:
python train_BayesByBackprop_MNIST.py -hLes meilleurs résultats sont obtenus avec un Laplace Prior.
(https://arxiv.org/abs/1506.02557)
Bayes par inférence de rétroprople où la moyenne et la variance des activations sont calculées en forme fermée. Les activations sont échantillonnées au lieu de poids. Cela rend la variance de l'échelle de l'estimateur de Monte Carlo Elbo comme 1 / m, où m est la taille du minibatch. Échantillonnage des échelles d'échelles (M-1) / m. La divergence de KL entre les Gaussiens peut également être calculée sous forme fermée, ce qui réduit encore la variance. Le calcul de chaque époque est plus rapide, tout comme la convergence.
Former un modèle sur MNIST:
python train_BayesByBackprop_MNIST.py --model Local_Reparam [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]](https://arxiv.org/abs/1506.02142)
Un taux d'abandon fixe de 0,5 est réglé.
Cadres de colab avec des modèles de régression: MC abandon
Former un modèle sur MNIST:
python train_MCDropout_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Pour une explication des arguments du script:
python train_MCDropout_MNIST.py -h(https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf)
Afin de converger vers le vrai postérieur sur W, le taux d'apprentissage doit être recuit selon les conditions de Robbins-Monro. En pratique, nous utilisons un taux d'apprentissage fixe.
Cadres de colab avec des modèles de régression: homoscédastique / hétéroscédastique SGLD
Former un modèle sur MNIST:
python train_SGLD_MNIST.py [--use_preconditioning [USE_PRECONDITIONING]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Pour une explication des arguments du script:
python train_SGLD_MNIST.py -h(https://arxiv.org/abs/1512.07666)
SGLD avec préconditionnement RMSProp. Un taux d'apprentissage plus élevé doit être utilisé que pour la vanille SGLD.
Former un modèle sur MNIST:
python train_SGLD_MNIST.py --use_preconditioning True [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Plusieurs réseaux sont formés sur des sous-échantillons de l'ensemble de données.
Cahiers de colab avec modèles de régression: carte l'ensemble homoscédastique / hétéroscédastique
Former un ensemble sur MNIST:
python train_Bootrap_Ensemble_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--subsample [SUBSAMPLE]] [--n_nets [N_NETS]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Pour une explication des arguments du script:
python train_Bootrap_Ensemble_MNIST.py -h(https://openreview.net/pdf?id=SKDVD2XAZ)
Former un réseau de carte, puis calculer une aproxiamtion de la série Taylor de second ordre à la courbure autour d'un mode de la postérieure. Une approximation de Hesse diagonale de bloc est utilisée, où seules les dépendances intra-couche sont prises en compte. La Hesse est en outre approximée en tant que produit Kronecker de l'attente des facteurs Hessian d'un seul point de données. Approximation de la Hesse peut prendre un certain temps. Heureusement, cela ne doit être fait qu'une seule fois.
Former un réseau de cartes sur MNIST et approximativement Hessian:
python train_KFLaplace_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--hessian_diag_sig [HESSIAN_DIAG_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Pour une explication des arguments du script:
python train_KFLaplace_MNIST.py -hNotez que nous économisons les facteurs de Hesse non à l'échelle et non inversés. Cela permettra des modifications bon marché en calcul de l'heure préalable au moment de l'inférence, car la Hessian n'aura pas besoin d'être recueillie. L'inférence nécessitera l'inversion des facteurs de Hesse approximés et l'échantillonnage d'une distribution normale de la matrice. Ceci est illustré dans les cahiers / kfac_laplace_mnist.ipynb
(https://arxiv.org/abs/1402.4102)
Nous mettons en œuvre la version adaptée à l'échelle de cet algorithme, proposé ici pour trouver automatiquement des hyperparamètres pendant Burn-In. Nous placons un primaire gaussien sur les poids du réseau et un hyperprior gamma sur la précision de la gaussienne.
Exécutez SG-HMC-SA Burn In et Sampler, en économisant des poids dans un fichier spécifié.
python train_SGHMC_MNIST.py [--epochs [EPOCHS]] [--sample_freq [SAMPLE_FREQ]] [--burn_in [BURN_IN]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Pour une explication des arguments du script:
python train_SGHMC_MNIST.py -hL'inférence de la carte fournit une estimation ponctuelle des valeurs des paramètres. Lorsqu'ils sont fournis avec des entrées hors distribution, telles que des chiffres tournés, ces modèles pour faire de mauvaises prédictions avec une grande confiance.
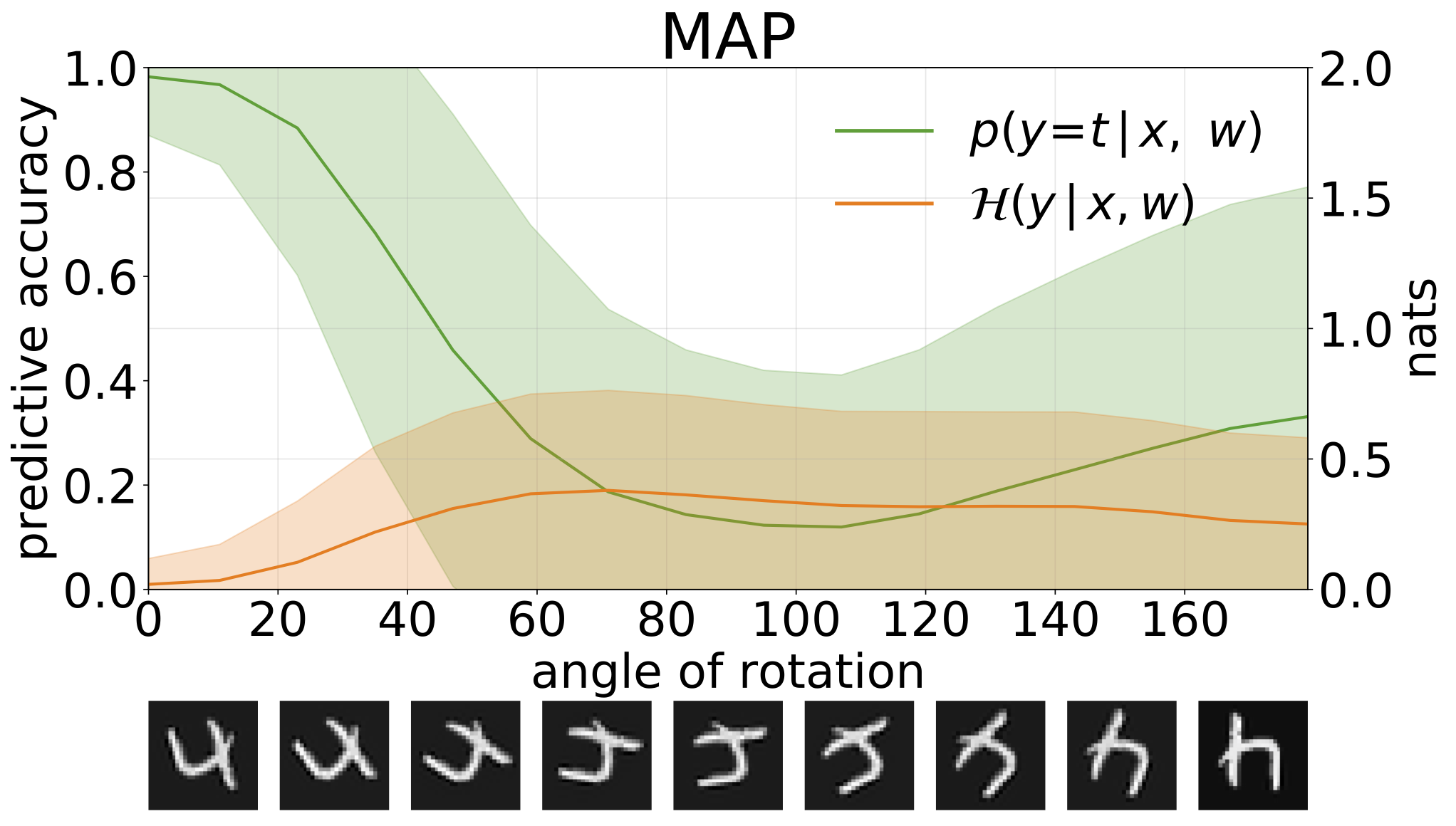
Nous pouvons mesurer l'incertitude dans les prévisions de nos modèles par l'entropie prédictive. Nous pouvons décomposer ce terme afin de distinguer 2 types d'incertitude. L'incertitude causée par le bruit dans les données, ou incertitude aléatorique , peut être quantifiée comme l'entropie attendue des prédictions du modèle. L'incertitude du modèle ou l'incertitude épistémique peut être mesurée comme la différence entre l'entropie totale et l'entropie aléatorique.
Tâche de régression homoscédastique jouet. Les données sont générées par un GP avec un noyau RBF (l = 1, σn = 0,3). Nous utilisons un réseau FC à sortie unique avec une couche cachée de 200 unités RELU pour prédire la moyenne de régression μ (x). Un log σ fixe est appris séparément.
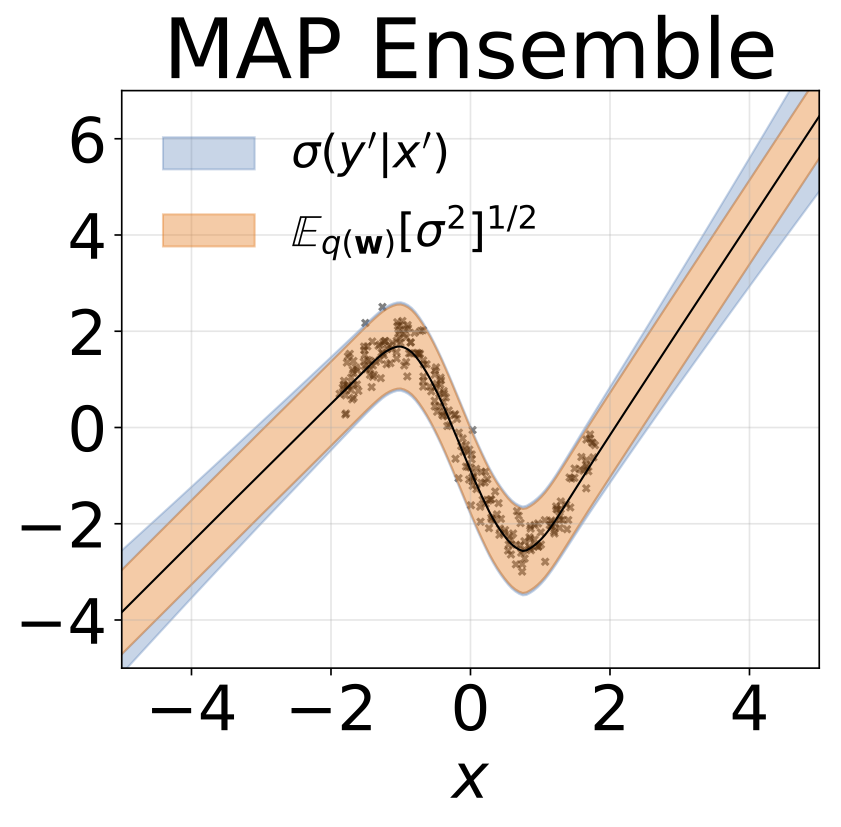
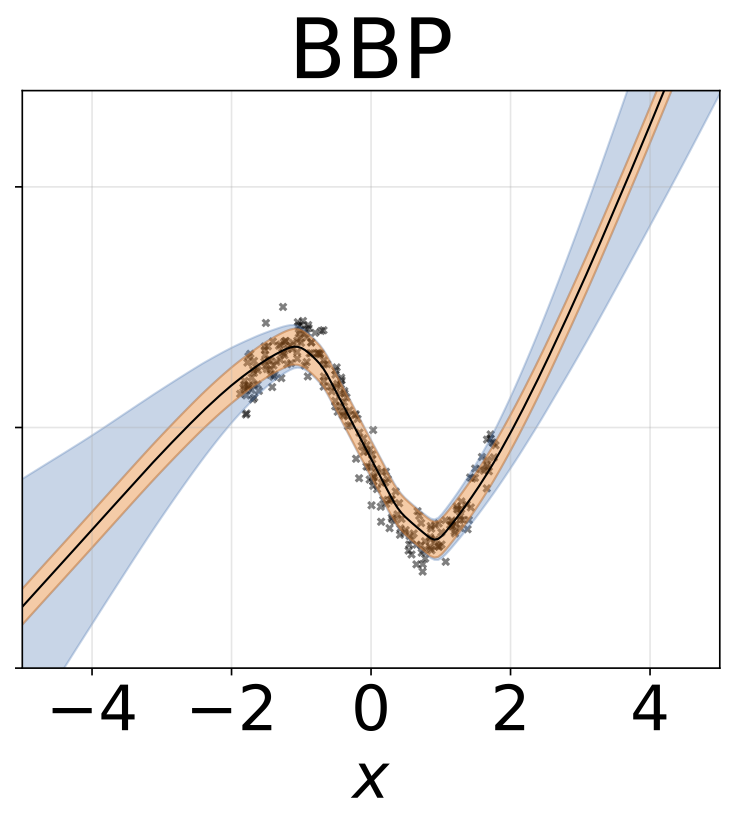
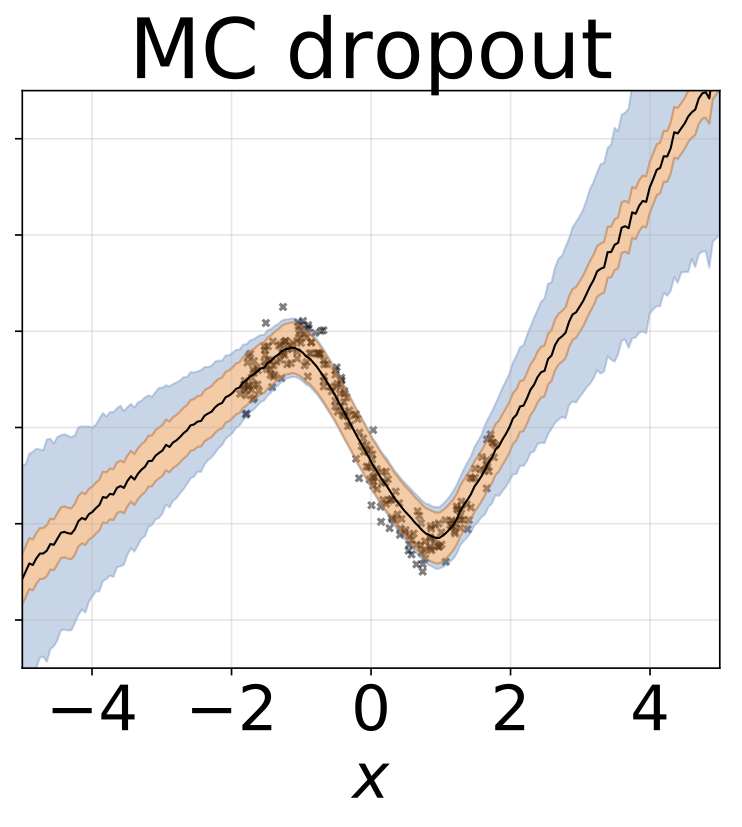
Même scénario que la section précédente mais log σ (x) est prédit à partir de l'entrée.
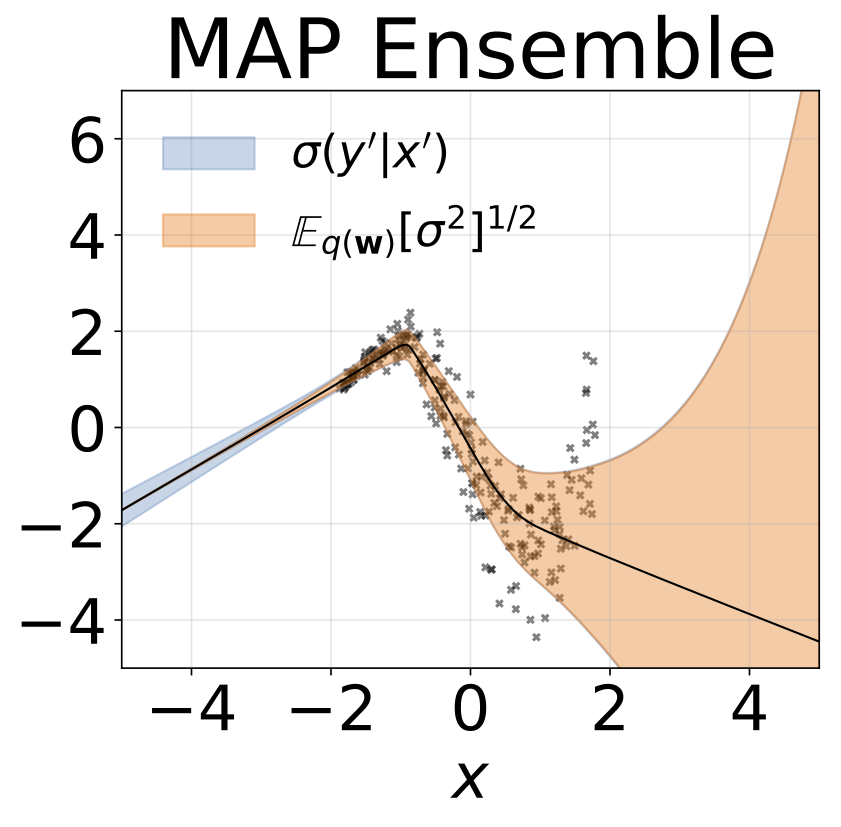
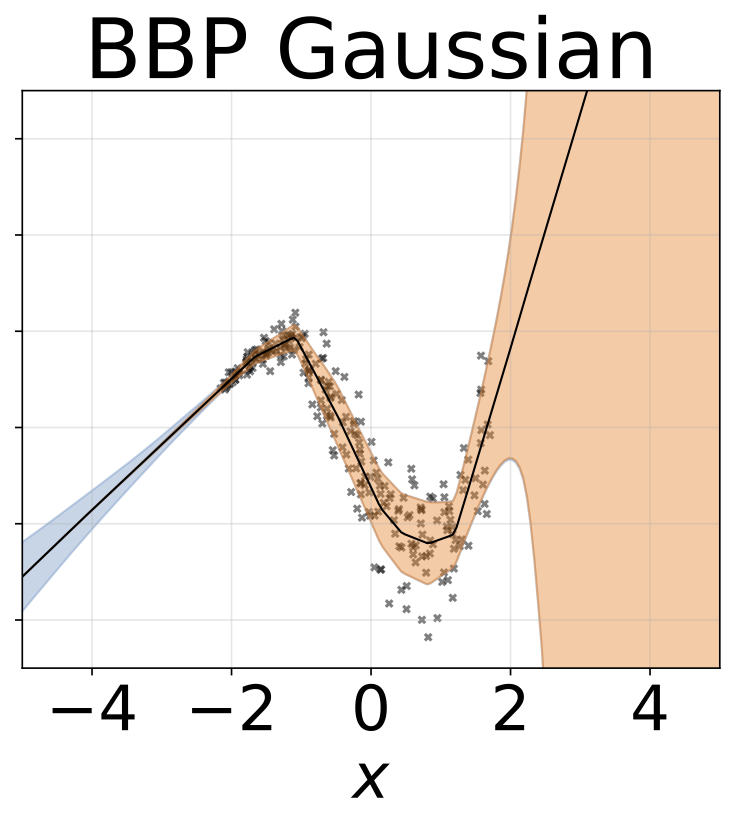
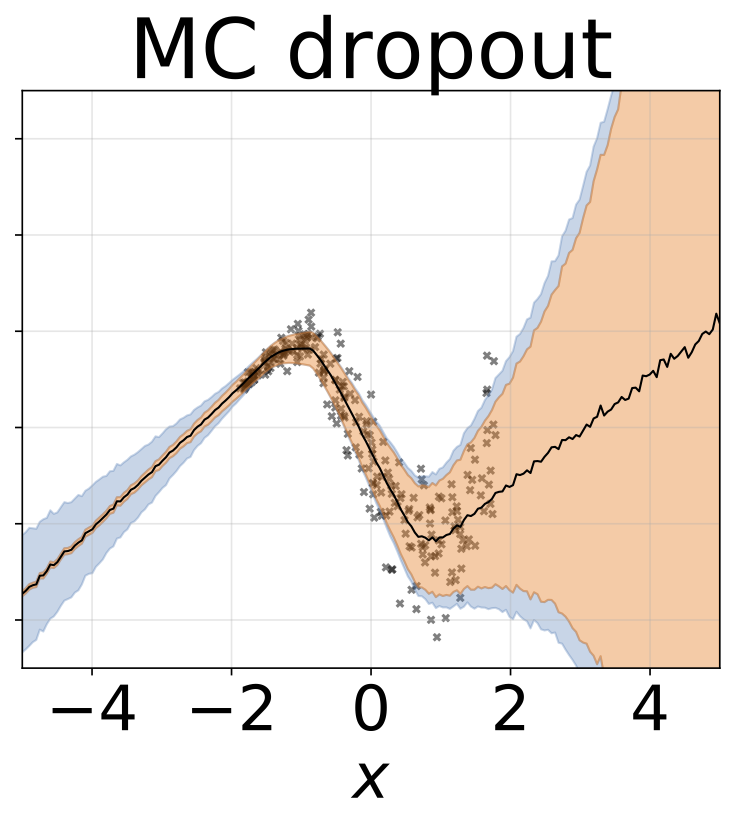
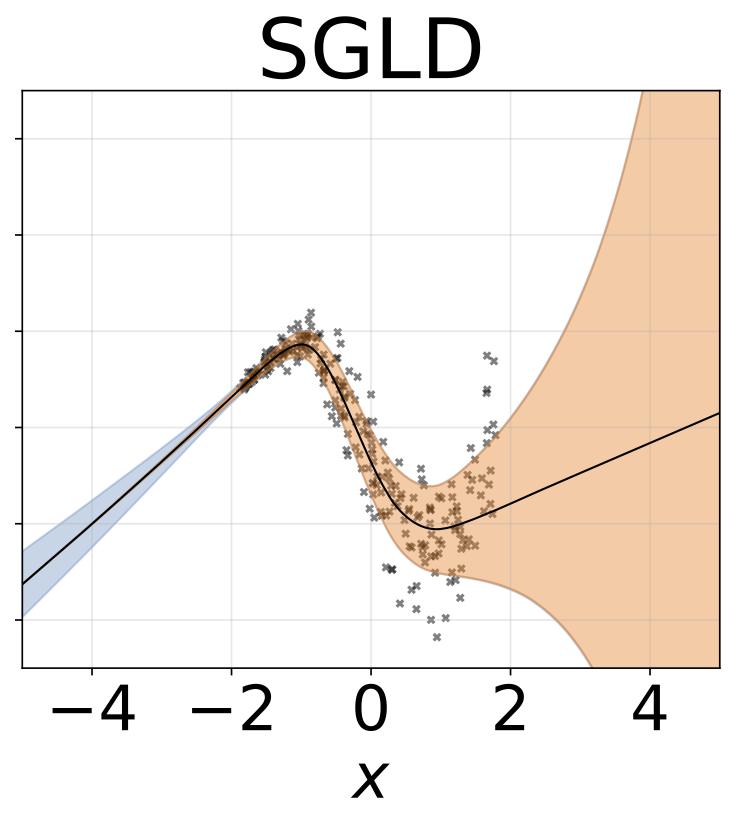
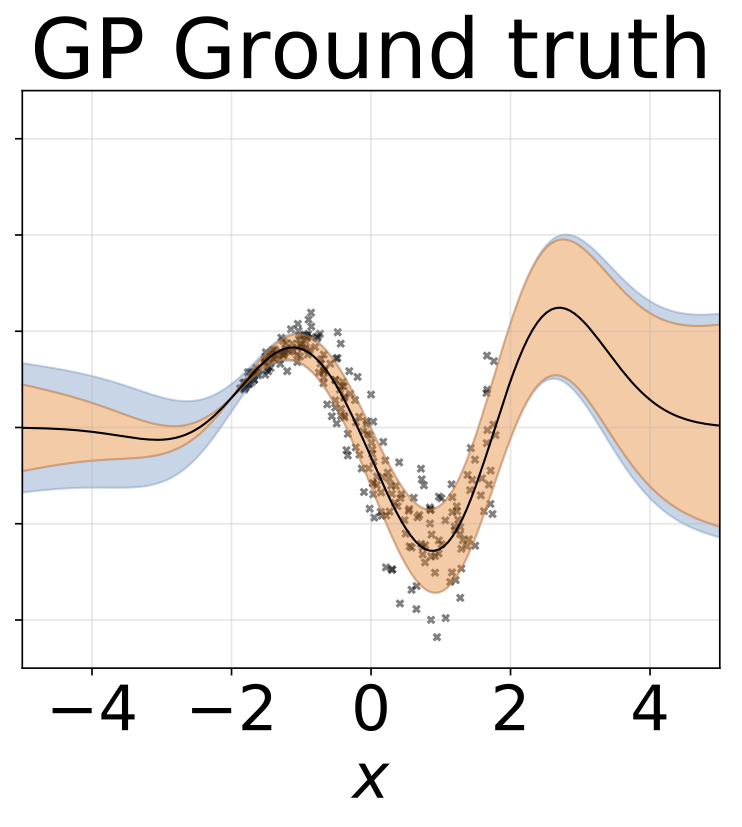
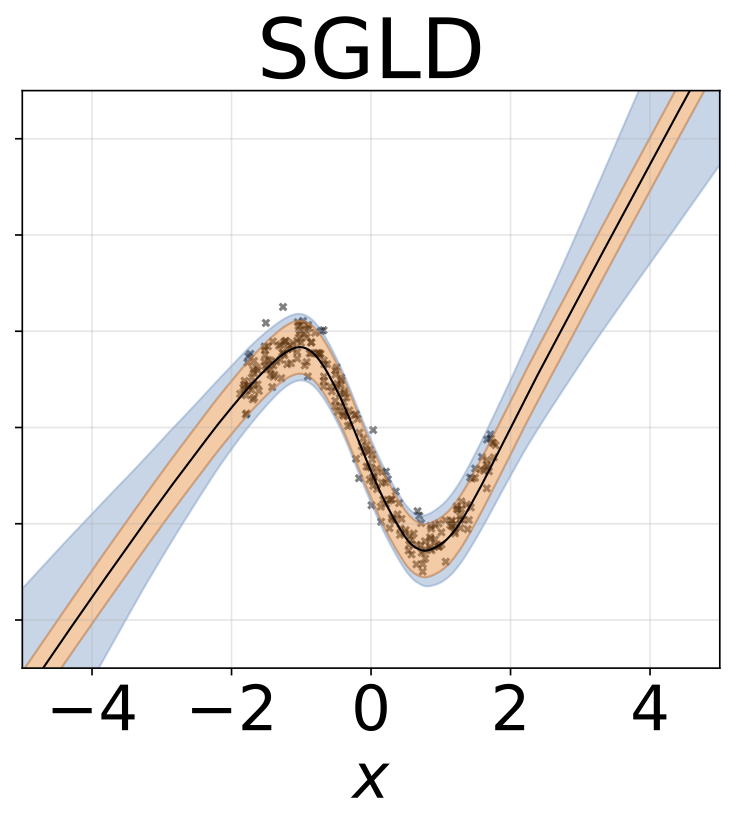
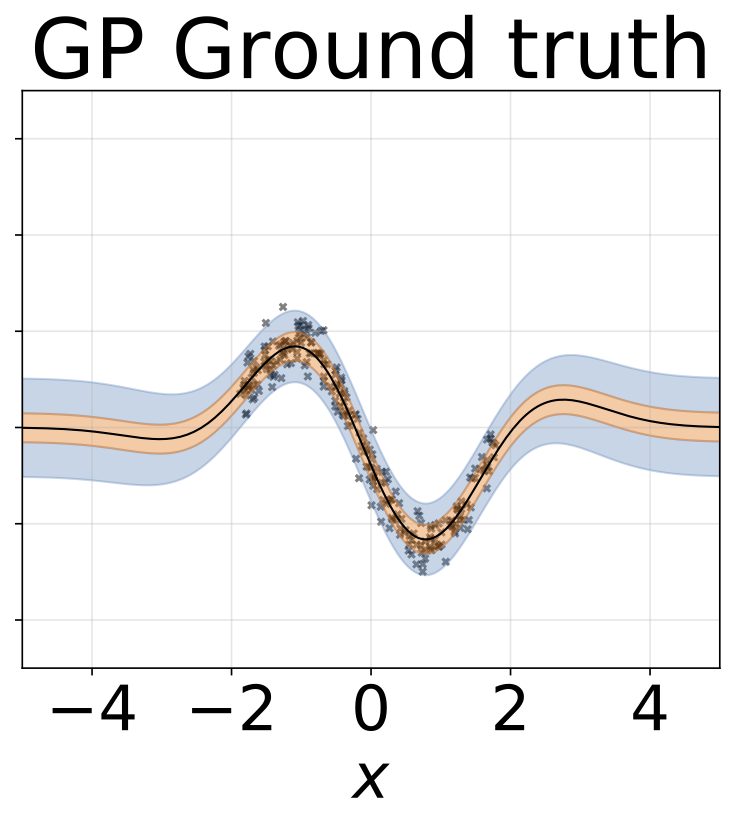
Tâche de régression hétéroscédastique jouet. Les données sont générées par un GP avec un noyau RBF (l = 1 σn = 0,3 · | x + 2 |). Nous utilisons un réseau à deux têtes avec 200 unités RELU pour prédire la moyenne de régression μ (x) et le log σ (x).
Nous avons effectué une régression hétéroscédastique sur les six ensembles de données UCI (boîtier, béton, efficacité énergétique, centrale électrique, vin rouge et jeux de données de yacht), en utilisant une validation croisée à 10 pieds. Toutes ces expériences sont contenues dans les cahiers hétéroscédastiques. Notez que les résultats dépendent fortement de la sélection des hyperparamètres. Les parcelles ci-dessous montrent des journaux log-vraiseaux et des RMSE dans le train (couleur semi-transparent) et test (couleur unie). Les cercles et les barres d'erreur correspondent respectivement à la moyenne de validation croisée de 10 fois respectivement.
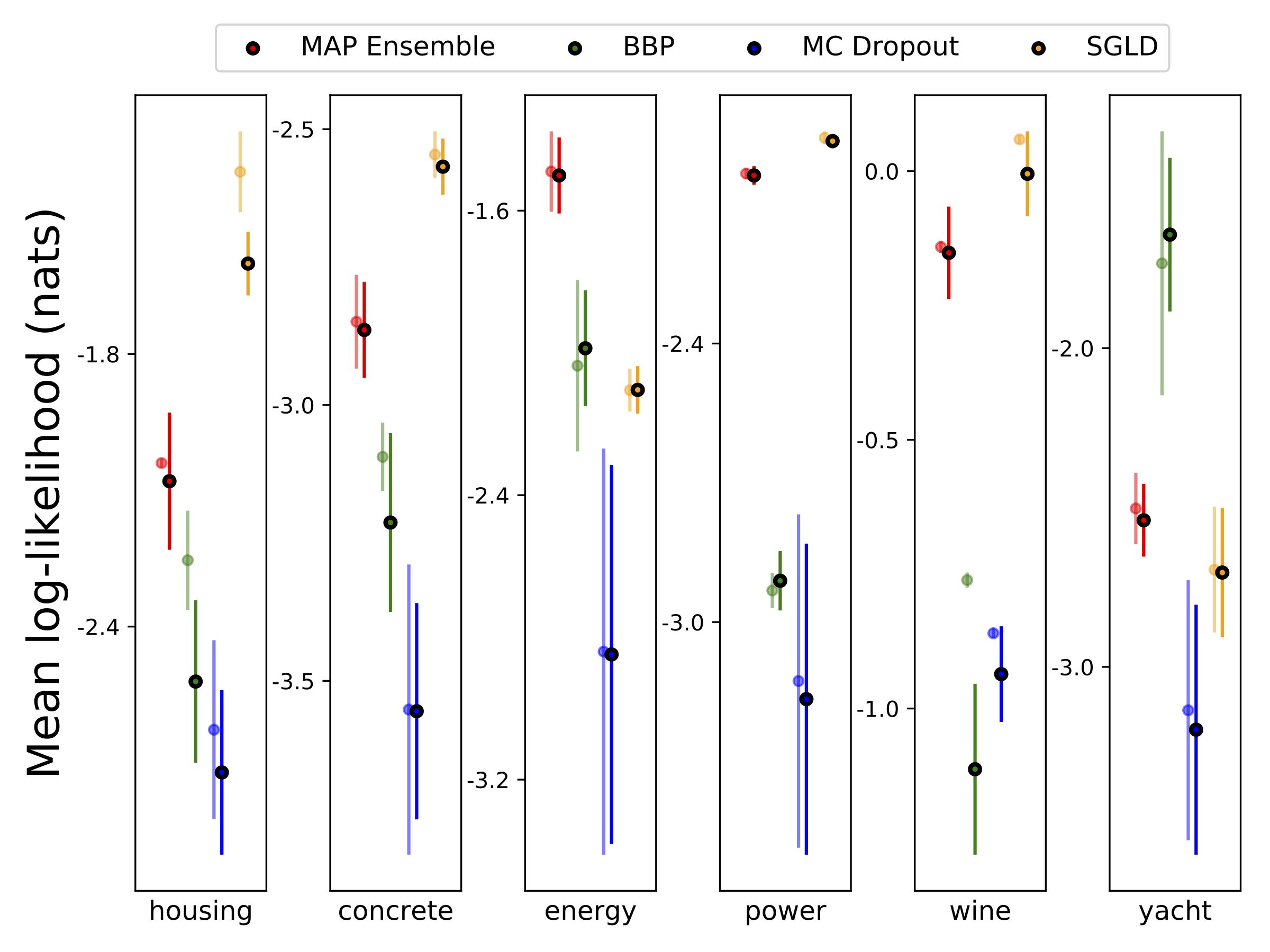
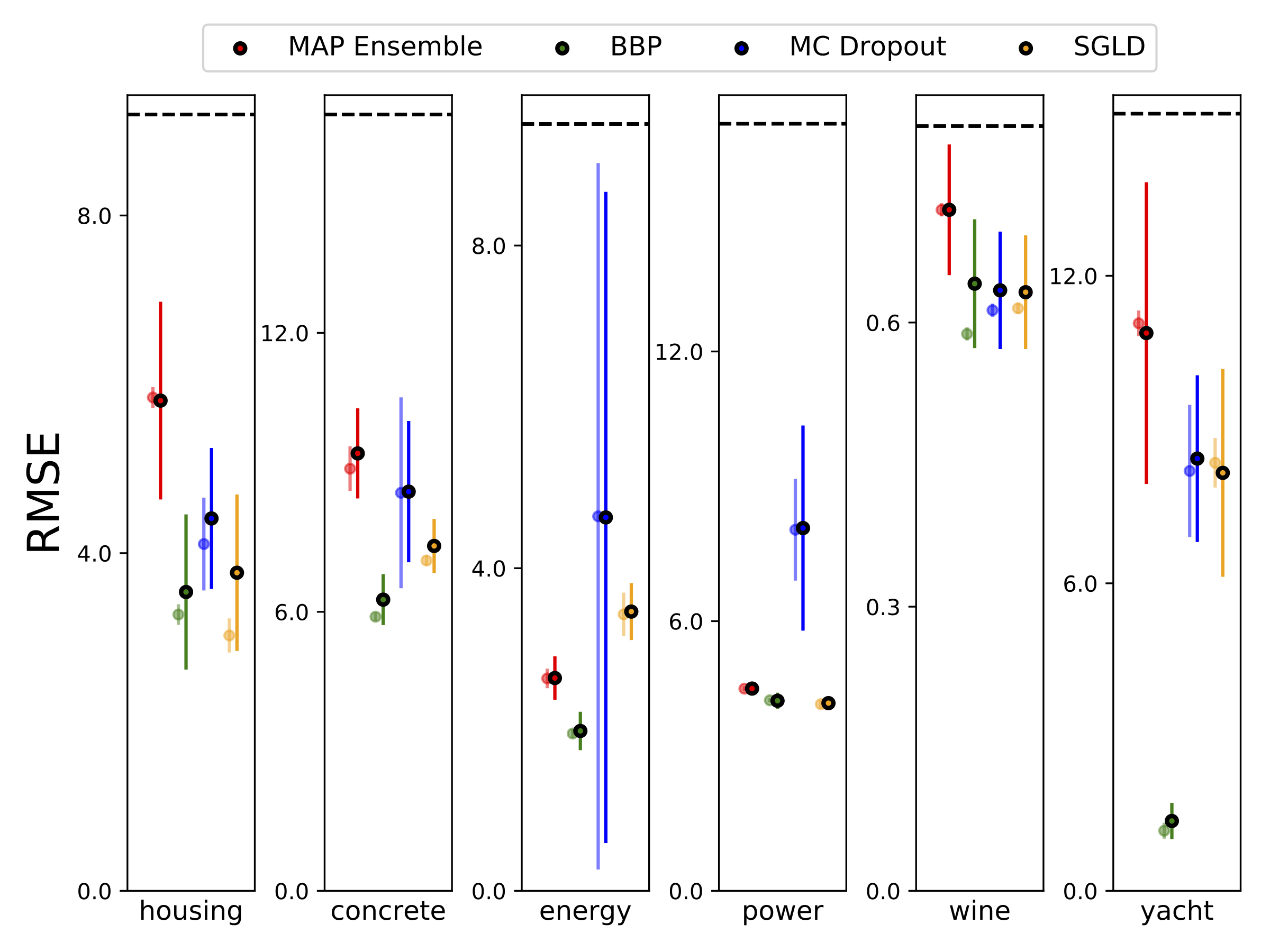
W est marginalisé avec 100 échantillons de poids pour tous les modèles sauf la carte, où un seul ensemble de poids est utilisé.
| Test MNIST | CARTE | Ensemble de cartes | BBP Gaussian | BBP GMM | BBP Laplace | BBP Reparam local | Décrocheur MC | SGLD | PSGLD |
|---|---|---|---|---|---|---|---|---|---|
| Se connecter comme | -572.9 | -496.54 | -1100.29 | -1008.28 | -892.85 | -1086.43 | -435.458 | -828.29 | -661.25 |
| Erreur % | 1.58 | 1.53 | 2.60 | 2.38 | 2.28 | 2.61 | 1.37 | 1.76 | 1.76 |
Résultats du test MNIST pour les méthodes considérées. L'un ouvrage hyperparamètre étendu n'a pas été effectué. Nous approximations de la distribution prédictive postérieure avec des échantillons de 100 mc. Nous utilisons un réseau FC avec deux couches RELU 1200 unitaires. S'il n'est pas spécifié, le prieur est gaussien avec STD = 0,1. P-SGLD utilise le préconditionnement RMSProp.
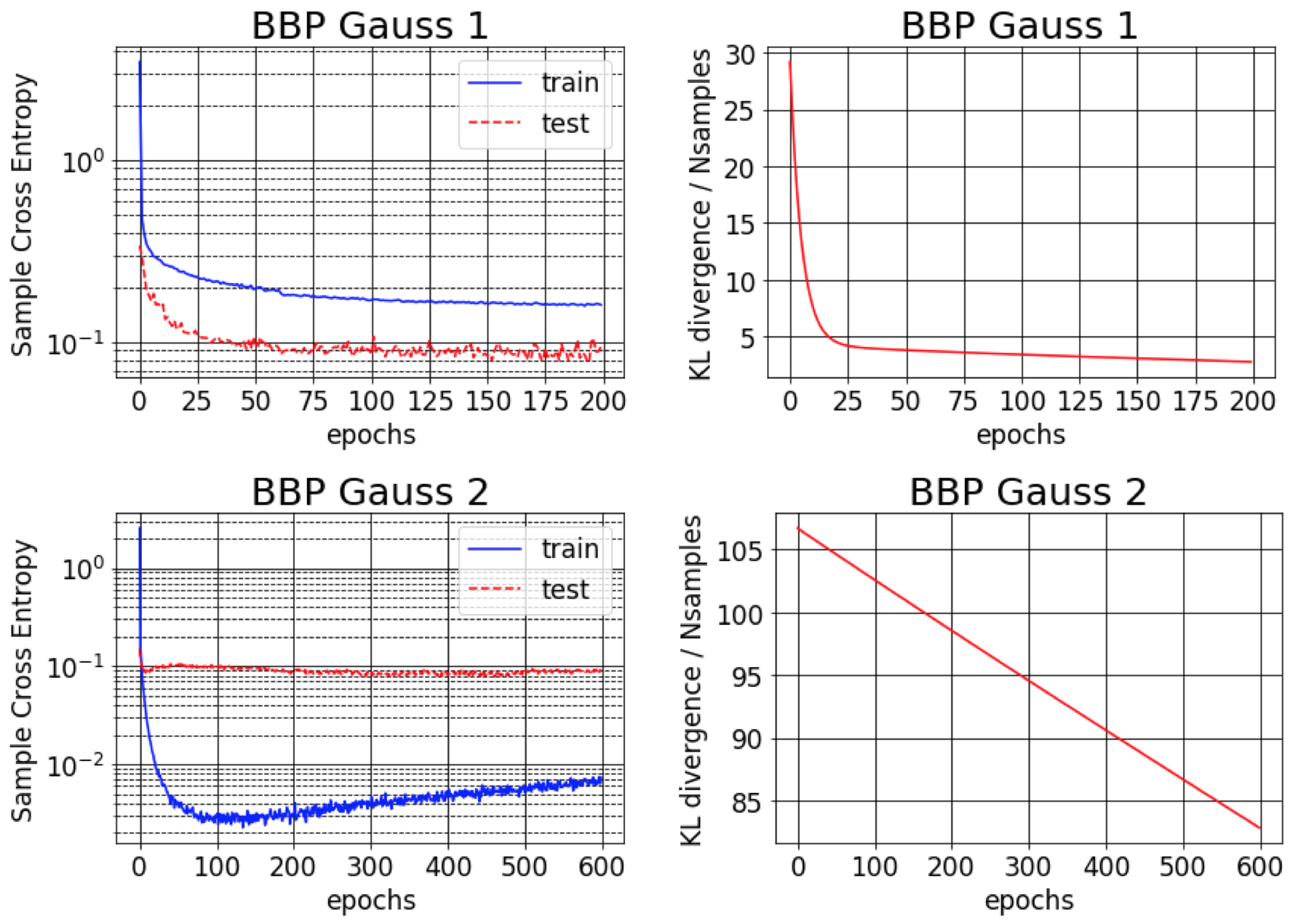
Le document d'origine pour Bayes by Backprop rapporte environ 1% d'erreur sur MNIST. Nous constatons que ce résultat ne peut être réalisable que si les variances postérieures approximatives sont initialisées pour être très petites (BBP Gauss 2). Dans ce scénario, les distributions sur les poids ressemblent à Deltas, donnant de bonnes performances prédictives mais de mauvaises estimations d'incertitude. Cependant, lors de l'initialisation des variances pour correspondre au préalable (BBP Gauss 1), nous obtenons les résultats ci-dessus. Les courbes de formation pour ces deux schémas de configuration d'hyperparamètre sont présentées ci-dessous:
Incertitudes totales, aléatoriques et épistémiques obtenues lors de la création d'échantillons OOD en augmentant l'ensemble de tests MNIST avec des rotations:
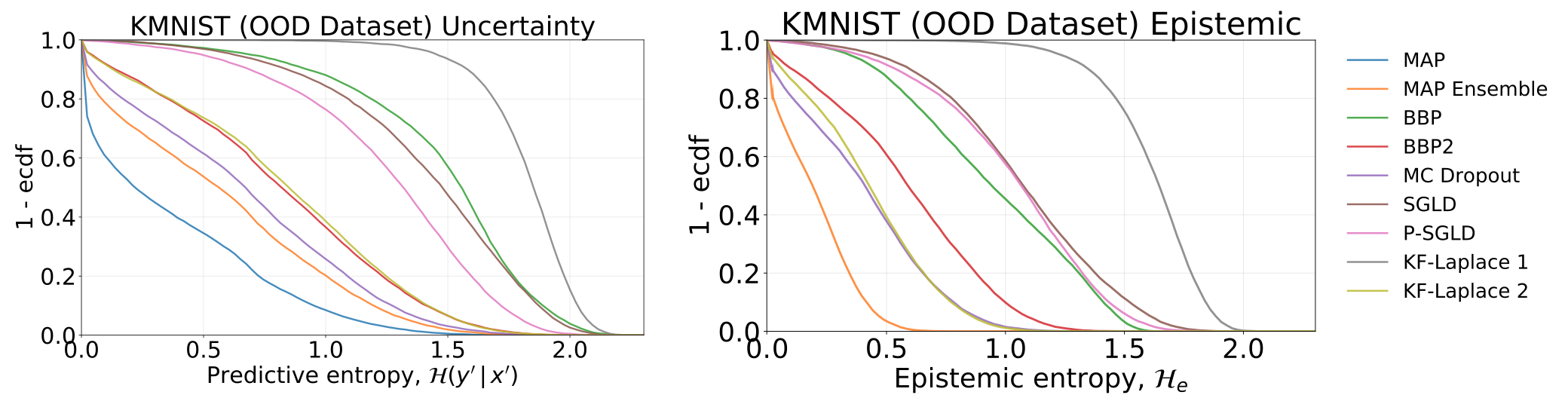
Incertitudes totales et épistémiques obtenues en testant nos modèles, - qui ont été formés sur MNIST -, sur l'ensemble de données KMNIST:
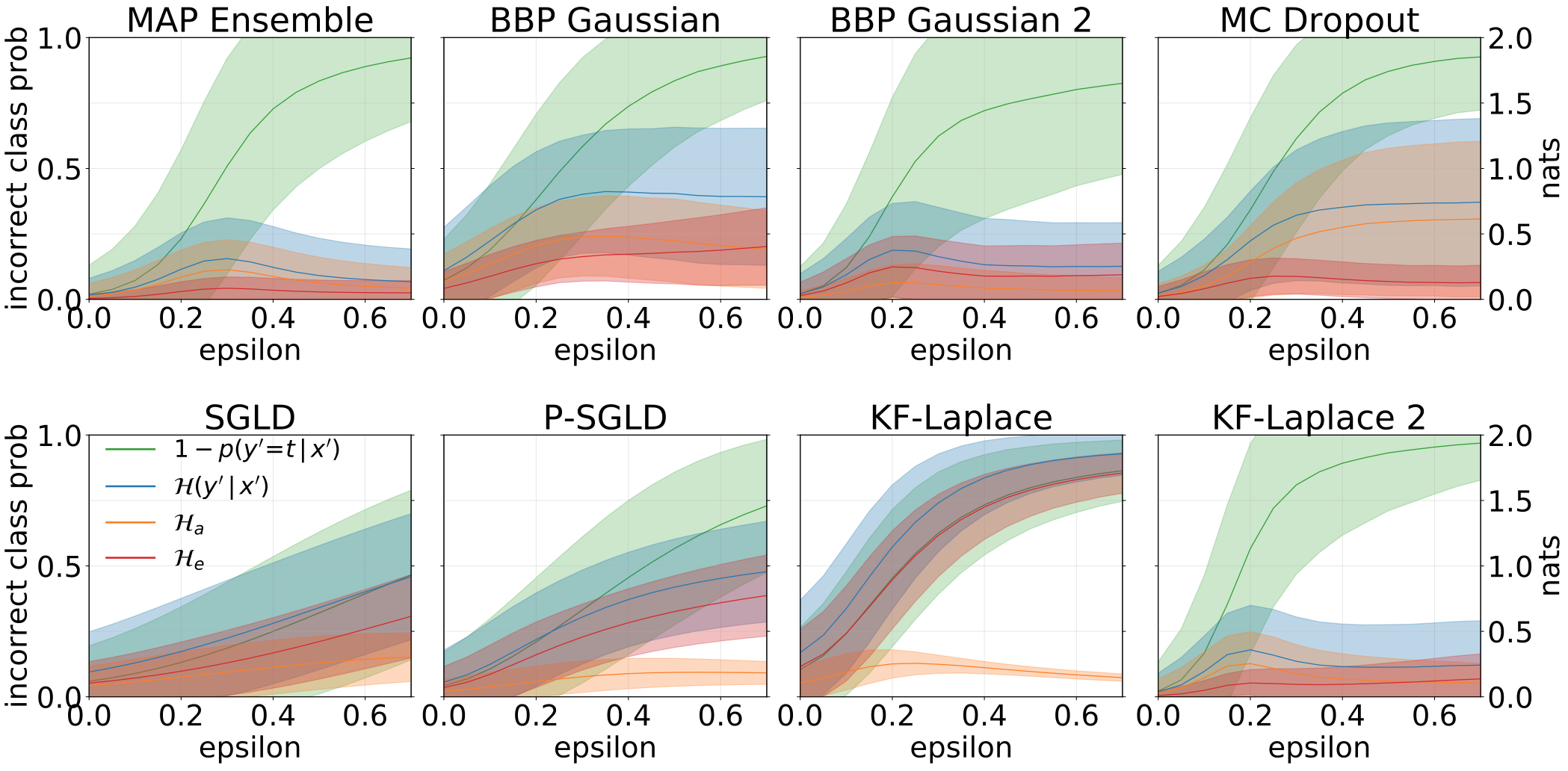
Incertitudes totales, aléatoriques et épistémiques obtenues lors de l'alimentation de nos modèles avec des échantillons adversaires (FGSM).
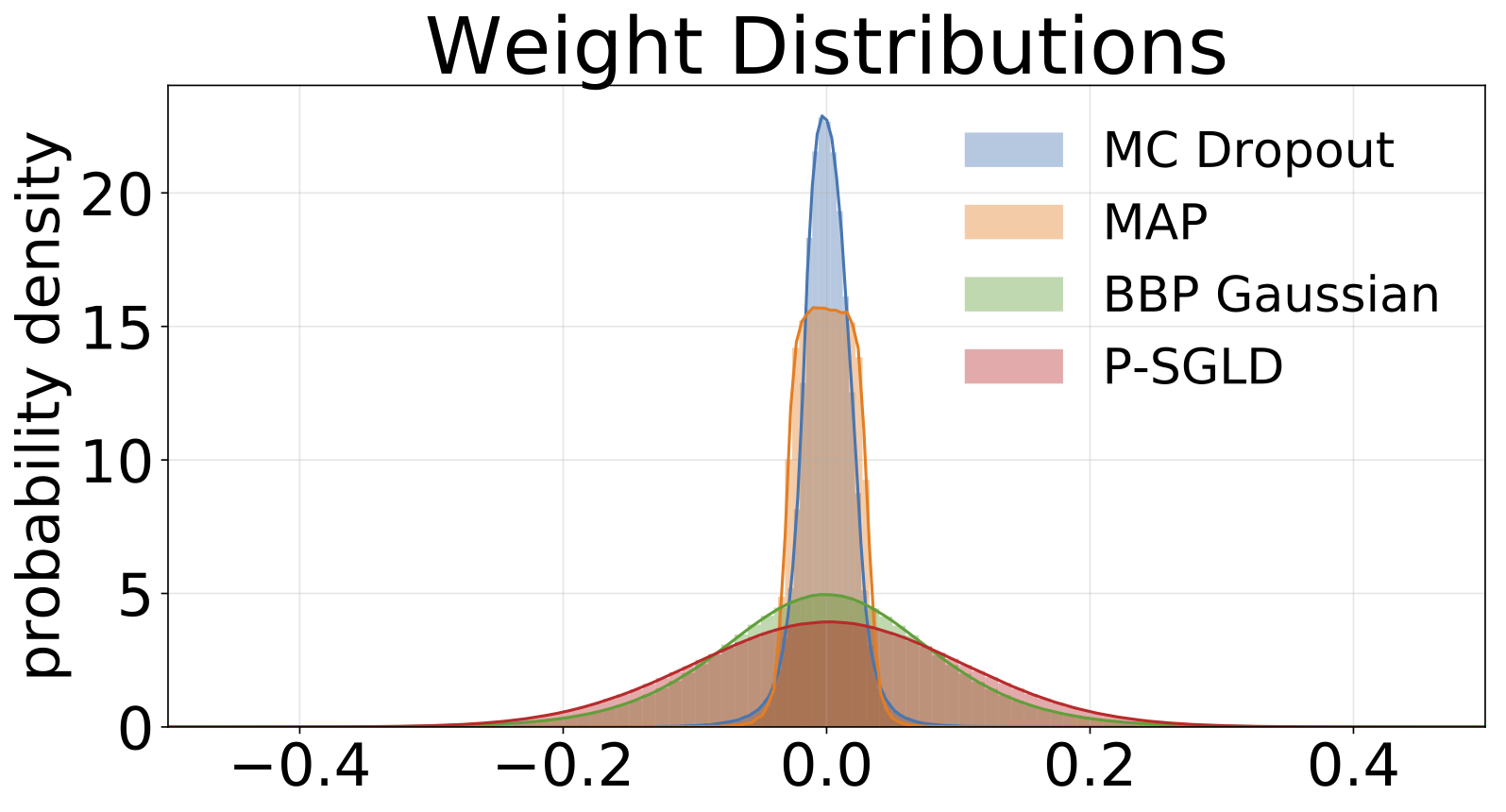
Des histogrammes de poids échantillonnés de chaque modèle formé sur MNIST. Nous dessions 10 échantillons de W pour chaque modèle.
#FAIRE