Implementaciones de Pytorch para los siguientes métodos de inferencia aproximada:
También proporcionamos código para:
El proyecto está escrito en Python 2.7 y Pytorch 1.0.1. Si CUDA está disponible, se usará automáticamente. Los modelos también pueden ejecutarse en CPU, ya que no son excesivamente grandes.
Llevamos a cabo experiencias de regresión homoscedástica y heteroscedástica en conjuntos de datos de juguetes, generados con (verdad gaussiana de tierra de proceso), así como en datos reales (seis conjuntos de datos UCI).
Cuadernos/clasificación/(ModelName) _ (ExperimentType) .IPYNB : Contiene experimentos utilizando (ModelName) ON (ExperimentType), es decir, homoscedastic/heteroscedastic. Los cuadernos heteroscedásticos contienen experimentos de conjuntos de datos de juguete y UCI para un dado (ModelName).
También proporcionamos cuadernos Google Colab. Esto significa que puedes ejecutar en una GPU (¡gratis!). No se requieren modificaciones: todas las dependencias y conjuntos de datos se agregan desde los cuadernos, excepto para seleccionar tiempo de ejecución -> Cambiar el tipo de tiempo de ejecución -> Acelerador de hardware -> GPU.
Train_ (ModelName) _ (DataSet) .py : Trains (ModelName) on (DataSet). Las métricas de capacitación y los pesos del modelo se guardarán en los directorios especificados.
SRC/ : Utilidades generales y definiciones de modelo.
Cuadernos/clasificación : un asort de cuadernos que permiten capacitación en modelos, evaluación y ejecución de experimentos de incertidumbre de rotación de dígitos. También permiten el trazado de distribución de peso y la poda de peso. Permiten la carga de modelos previamente capacitados para la experimentación.
(https://arxiv.org/abs/1505.05424)
Notebooks de Colab con modelos de regresión: BBP homoscedastic / heteroscedastic
Entrena un modelo en Mnist:
python train_BayesByBackprop_MNIST.py [--model [MODEL]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para una explicación de los argumentos del guión:
python train_BayesByBackprop_MNIST.py -hLos mejores resultados se obtienen con un Laplace anterior.
(https://arxiv.org/abs/1506.02557)
Bayes por inferencia backprop donde la media y la varianza de las activaciones se calculan en forma cerrada. Las activaciones se muestrean en lugar de pesos. Esto hace que la varianza de la escala del estimador de Monte Carlo elbo como 1/m, donde M es el tamaño del minibatch. Escalas de pesas de muestreo (M-1)/m. La divergencia de KL entre los gaussianos también se puede calcular en forma cerrada, reduciendo aún más la varianza. El cálculo de cada época es más rápido y también lo es la convergencia.
Entrena un modelo en Mnist:
python train_BayesByBackprop_MNIST.py --model Local_Reparam [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--n_samples [N_SAMPLES]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]](https://arxiv.org/abs/1506.02142)
Se establece una tasa de abandono fija de 0.5.
Notebooks Colab con modelos de regresión: MC Descarga Homoscedastic Heterocedastic
Entrena un modelo en Mnist:
python train_MCDropout_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para una explicación de los argumentos del guión:
python train_MCDropout_MNIST.py -h(https://www.ics.uci.edu/~welling/publications/papers/stoclangevin_v6.pdf)
Para converger a la verdadera posterior sobre W, la tasa de aprendizaje debe recocirse de acuerdo con las condiciones de Robbins-Monro. En la práctica, utilizamos una tasa de aprendizaje fija.
Notebooks de Colab con modelos de regresión: SGLD homoscedastic / heteroscedastic
Entrena un modelo en Mnist:
python train_SGLD_MNIST.py [--use_preconditioning [USE_PRECONDITIONING]] [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para una explicación de los argumentos del guión:
python train_SGLD_MNIST.py -h(https://arxiv.org/abs/1512.07666)
SGLD con preacondicionamiento RMSProp. Se debe usar una tasa de aprendizaje más alta que para el SGLD de vainilla.
Entrena un modelo en Mnist:
python train_SGLD_MNIST.py --use_preconditioning True [--prior_sig [PRIOR_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Múltiples redes están capacitadas en submuestras del conjunto de datos.
Notebooks de Colab con modelos de regresión: Maple Ensemble Homoscedastic / Heteroscedastic
Entrena un conjunto en Mnist:
python train_Bootrap_Ensemble_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--subsample [SUBSAMPLE]] [--n_nets [N_NETS]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para una explicación de los argumentos del guión:
python train_Bootrap_Ensemble_MNIST.py -h(https://openreview.net/pdf?id=skdvd2xaz)
Entrene una red de mapas y luego calcule una serie de la serie Taylor de segundo orden a la curvatura alrededor de un modo de la parte posterior. Se utiliza una aproximación de Hesse Diagonal de bloque, donde solo se tienen en cuenta las dependencias intra capazas. El Hessian se aproxima más como el producto Kronecker de la expectativa de los factores de Hesse de un solo punto de datos. Aproximarse al Hesse puede llevar un tiempo. Afortunadamente solo debe hacerse una vez.
Entrena una red de mapas en Mnist y aproximado de Hessian:
python train_KFLaplace_MNIST.py [--weight_decay [WEIGHT_DECAY]] [--hessian_diag_sig [HESSIAN_DIAG_SIG]] [--epochs [EPOCHS]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para una explicación de los argumentos del guión:
python train_KFLaplace_MNIST.py -hTenga en cuenta que salvamos los factores de Hessianos sin invertir y sin incluir. Esto permitirá cambios computacionalmente baratos en el anterior en el momento de la inferencia, ya que el Hessian no necesitará ser computado. La inferencia requerirá invertir los factores de hessia aproximados y el muestreo de una distribución normal de la matriz. Esto se muestra en cuadernos/kfac_laplace_mnist.ipynb
(https://arxiv.org/abs/1402.4102)
Implementamos la versión adaptada a la escala de este algoritmo, propuesta aquí para encontrar hiperparámetros automáticamente durante el quemado. Colocamos un gaussiano previo sobre pesas de red y un gamma hiperprior sobre la precisión del gaussiano.
Ejecute SG-HMC-SA Burn In y Sampler, guardando pesos en el archivo especificado.
python train_SGHMC_MNIST.py [--epochs [EPOCHS]] [--sample_freq [SAMPLE_FREQ]] [--burn_in [BURN_IN]] [--lr [LR]] [--models_dir [MODELS_DIR]] [--results_dir [RESULTS_DIR]]Para una explicación de los argumentos del guión:
python train_SGHMC_MNIST.py -hLa inferencia de mapas proporciona una estimación puntual de los valores de parámetros. Cuando se les proporciona entradas fuera de distribución, como dígitos girados, estos modelos para hacer predicciones equivocadas con alta confianza.
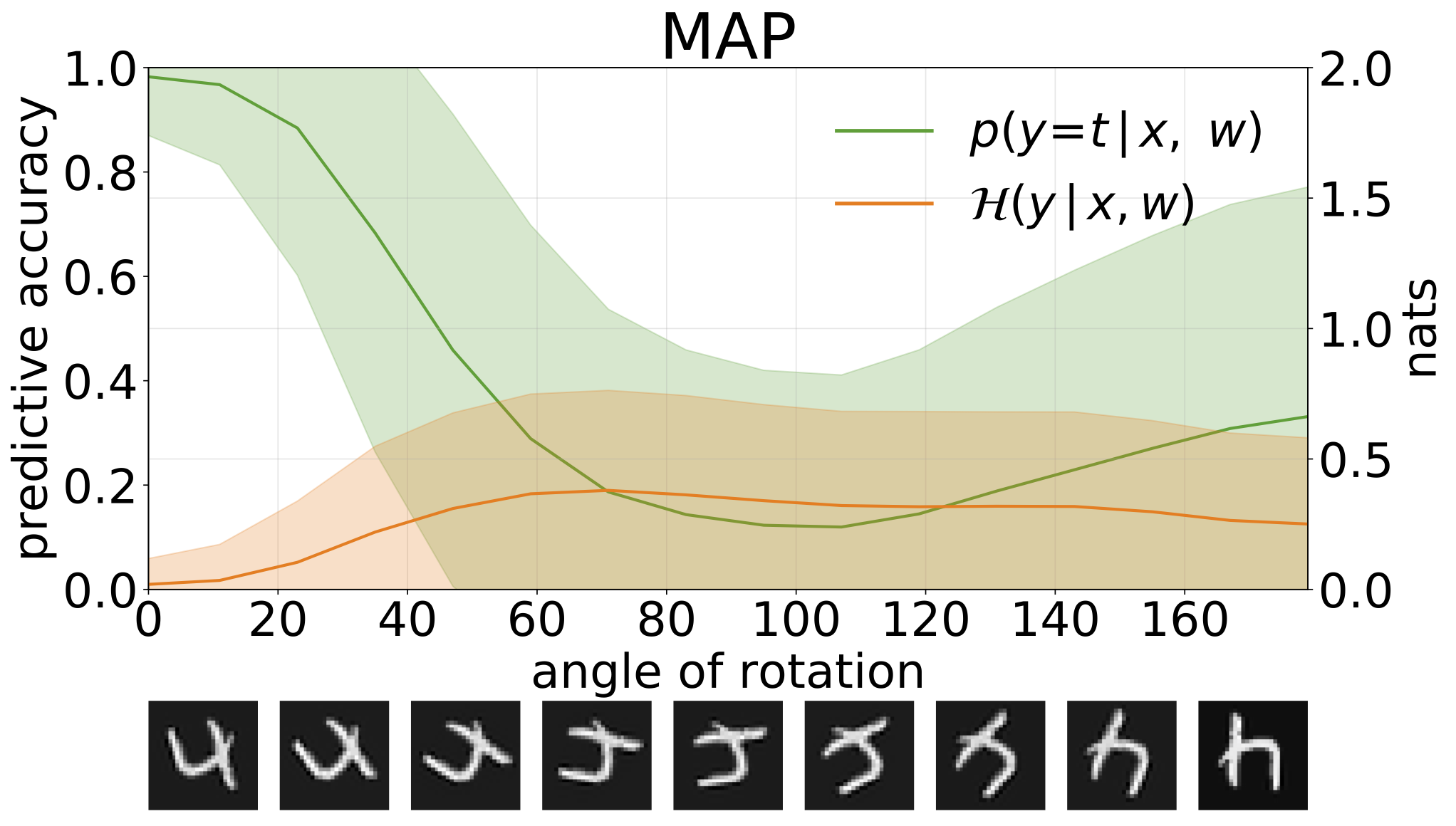
Podemos medir la incertidumbre en las predicciones de nuestros modelos a través de la entropía predictiva. Podemos descomponer este término para distinguir entre 2 tipos de incertidumbre. La incertidumbre causada por el ruido en los datos, o la incertidumbre aleatórica , puede cuantificarse como la entropía esperada de las predicciones del modelo. La incertidumbre del modelo o la incertidumbre epistémica se pueden medir como la diferencia entre la entropía total y la entropía aleatórica.
Tarea de regresión homoscedástica de juguete. Los datos son generados por un GP con un núcleo RBF (l = 1, σn = 0.3). Utilizamos una red FC de salida única con una capa oculta de 200 unidades RELU para predecir la media de regresión μ (x). Un registro fijo σ se aprende por separado.
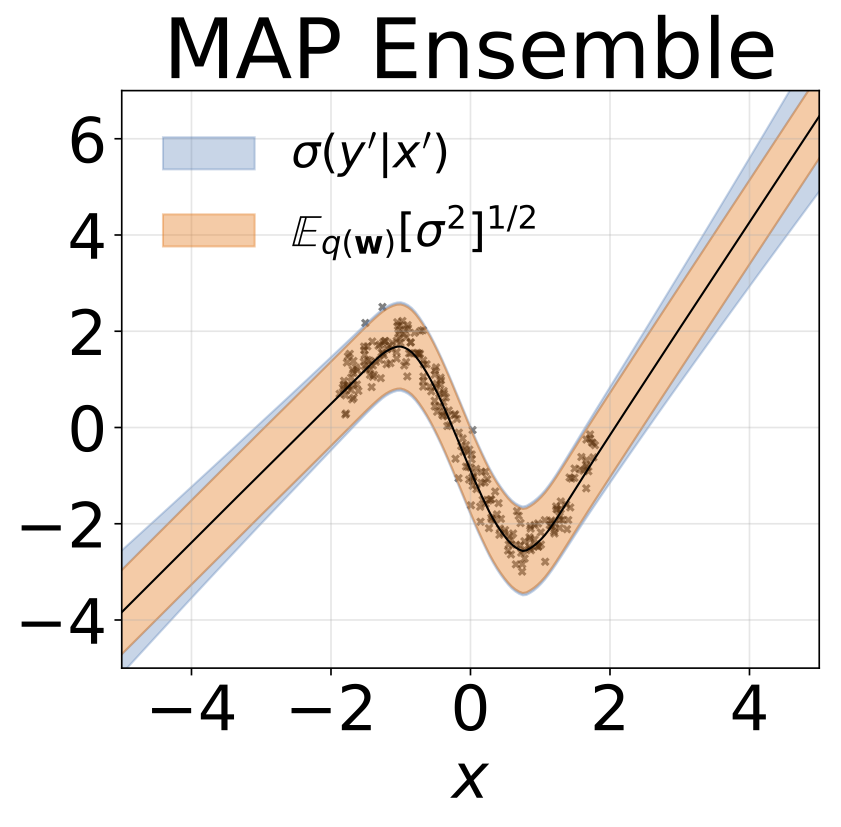
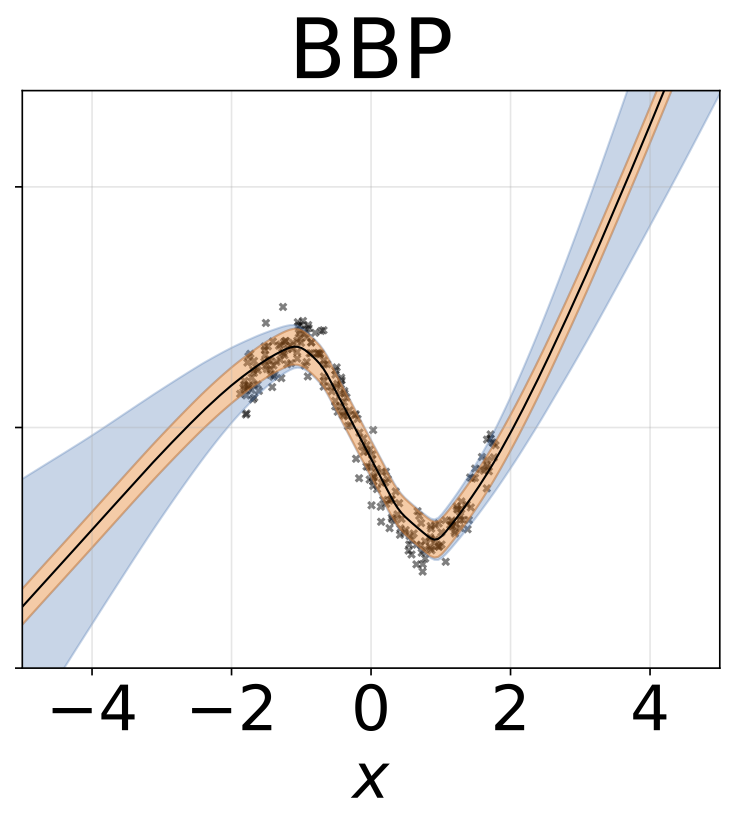
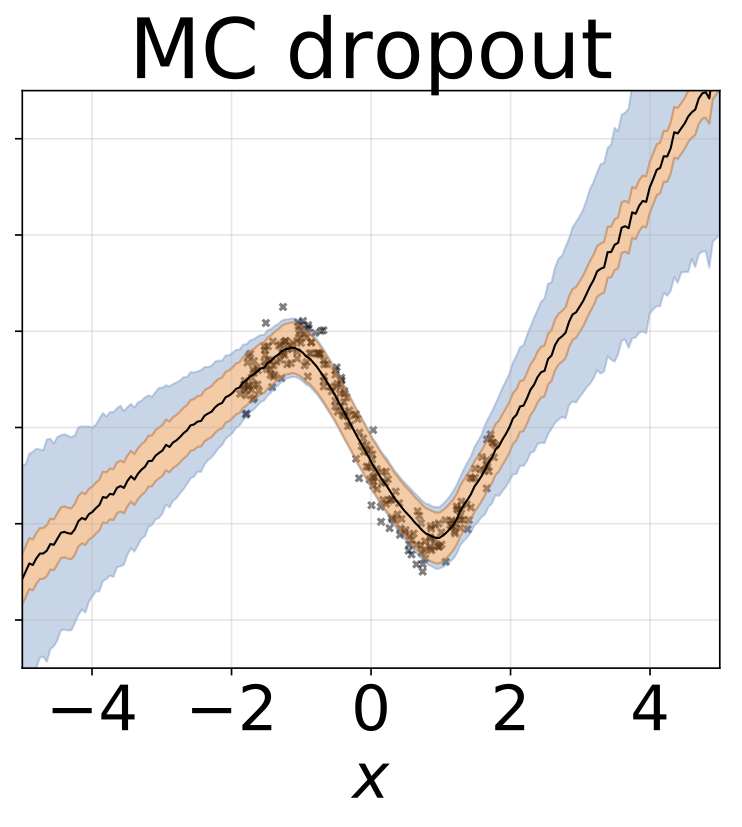
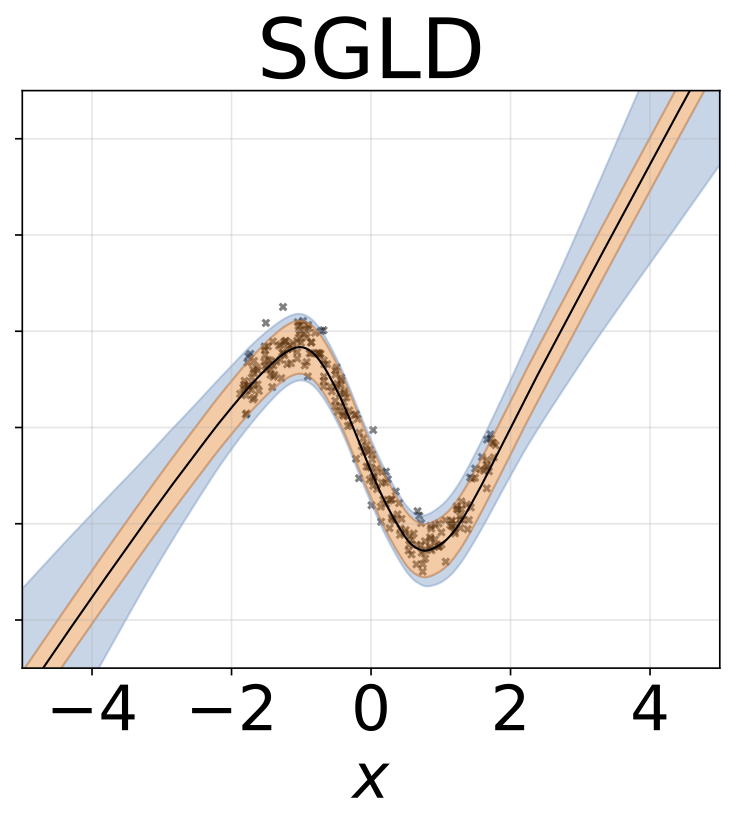
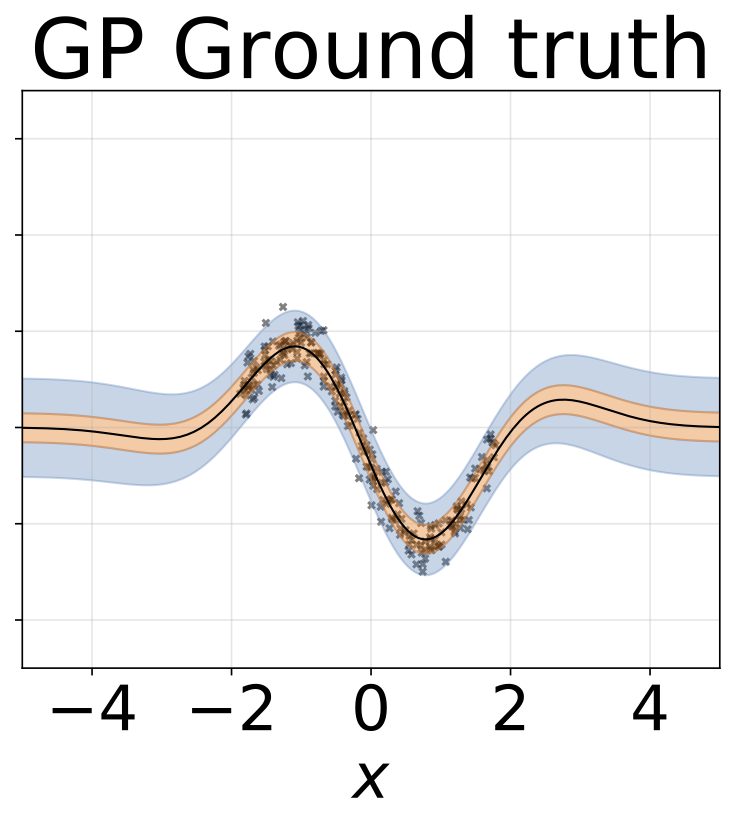
El mismo escenario que la sección anterior pero log σ (x) se predice a partir de la entrada.
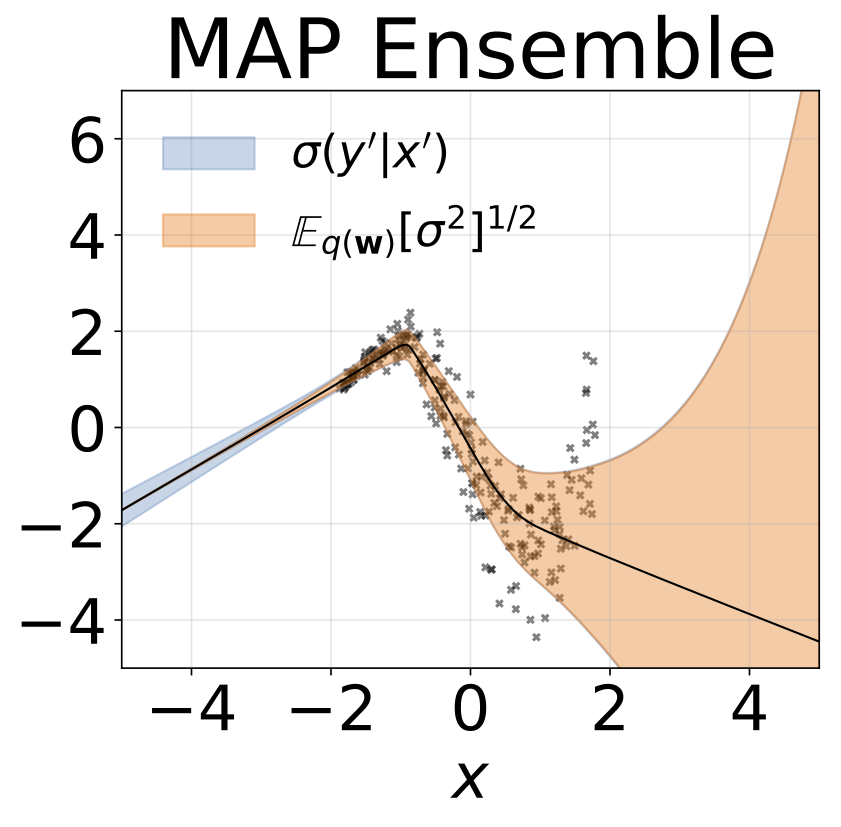
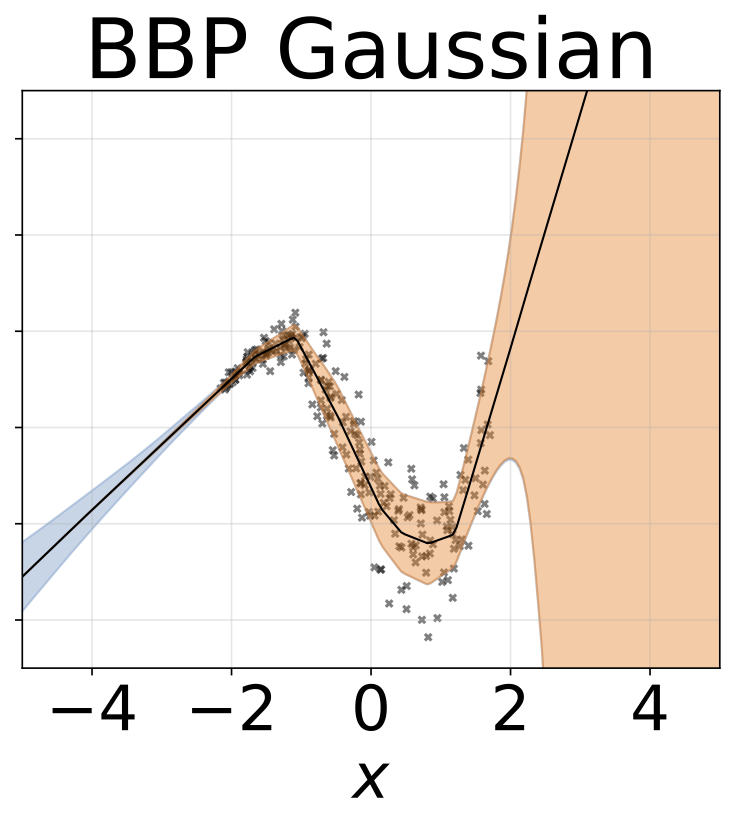
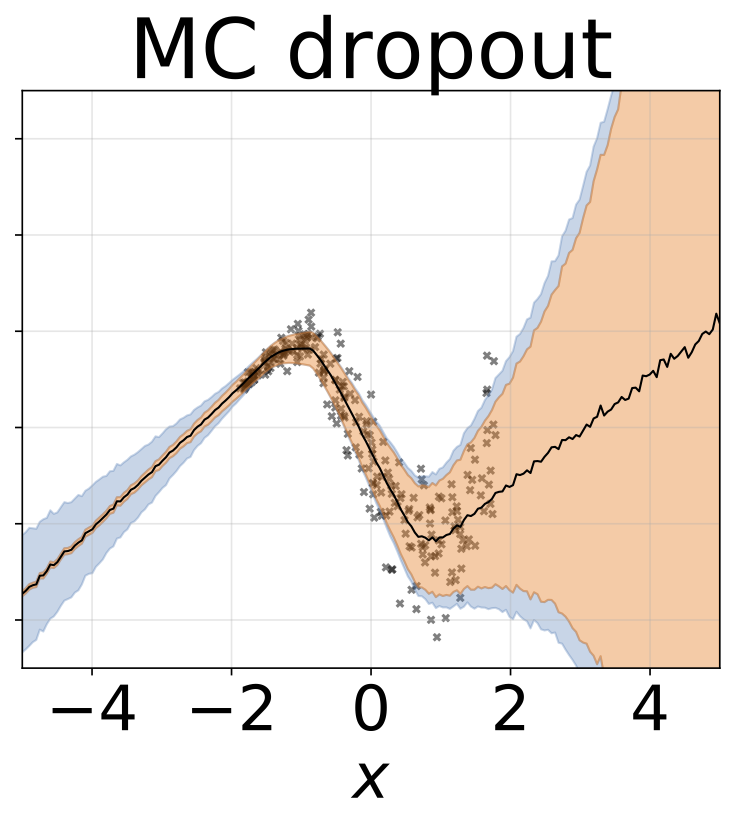
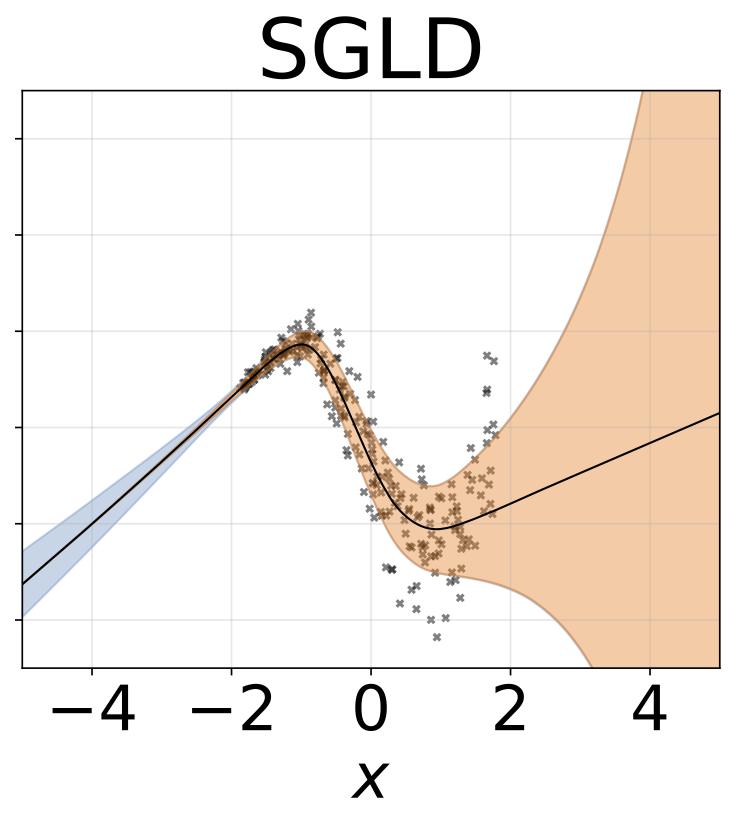
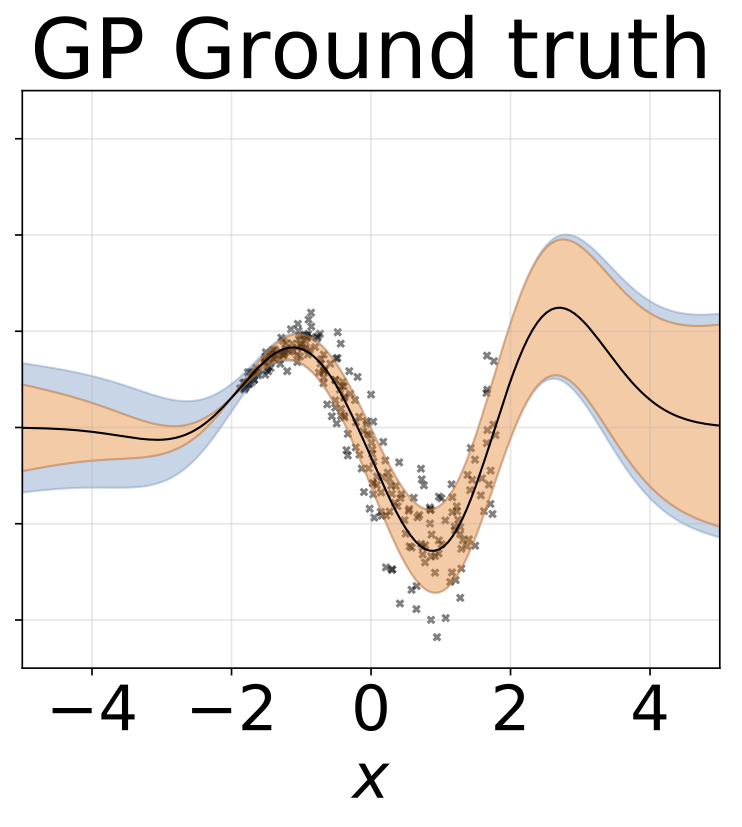
Tarea de regresión heteroscedástica de juguete. Los datos son generados por un GP con un núcleo RBF (l = 1 σn = 0.3 · | x + 2 |). Utilizamos una red de dos cabezas con 200 unidades RELU para predecir la media de regresión μ (x) y el registro de desviación estandilial σ (x).
Realizamos una regresión heteroscedástica en los seis conjuntos de datos UCI (alojamiento, concreto, eficiencia energética, planta de energía, vino tinto y conjuntos de datos de yates), utilizando validación cruzada de 10 valores. Todos estos experimentos están contenidos en los cuadernos heteroscedásticos. Tenga en cuenta que los resultados dependen en gran medida de la selección de hiperparameter. Las gráficas a continuación muestran log-Likelies y RMSE en el tren (color semitransparente) y prueba (color sólido). Los círculos y las barras de error corresponden a la media de validación cruzada de 10 veces y las desviaciones estándar, respectivamente.
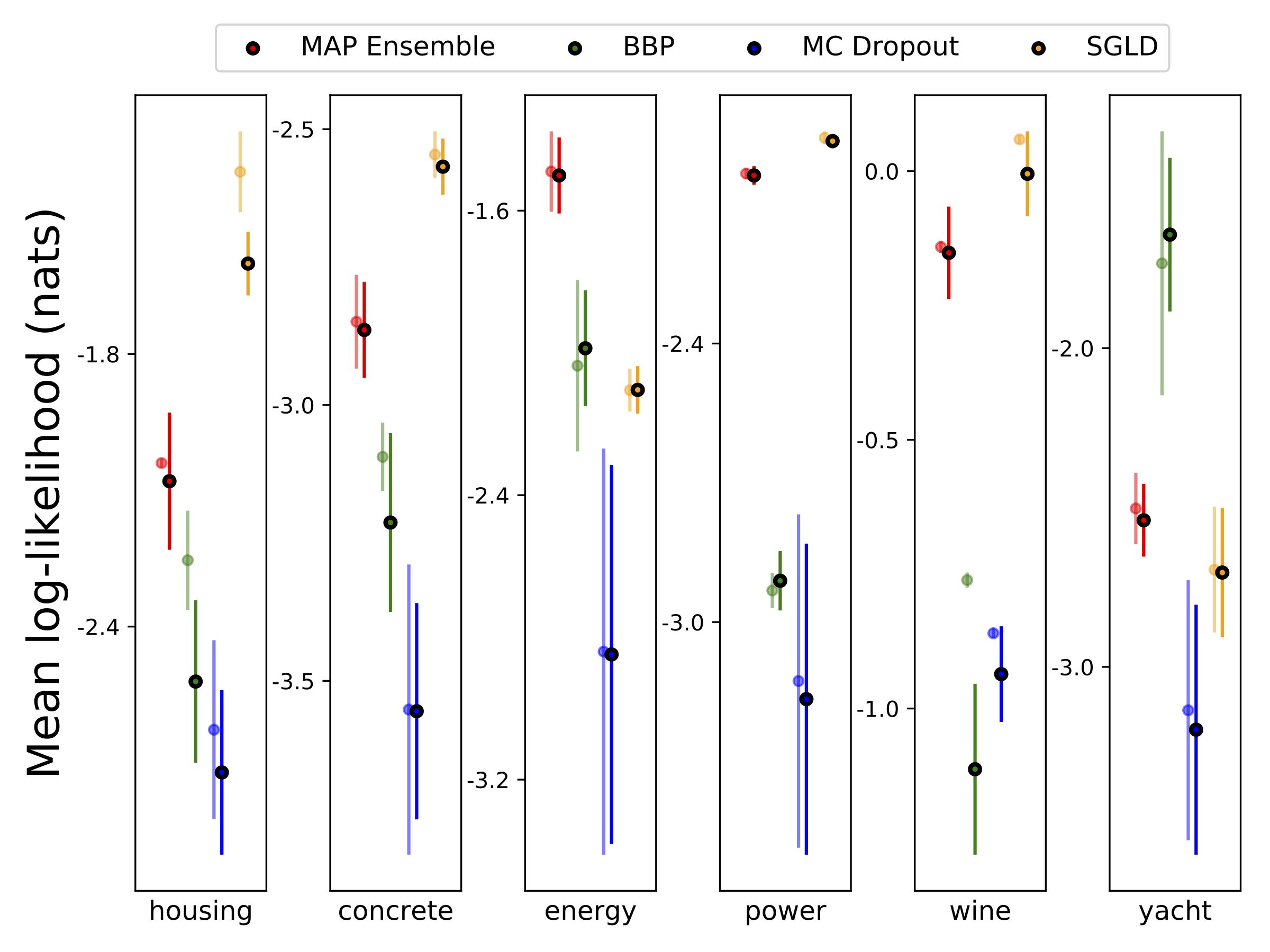
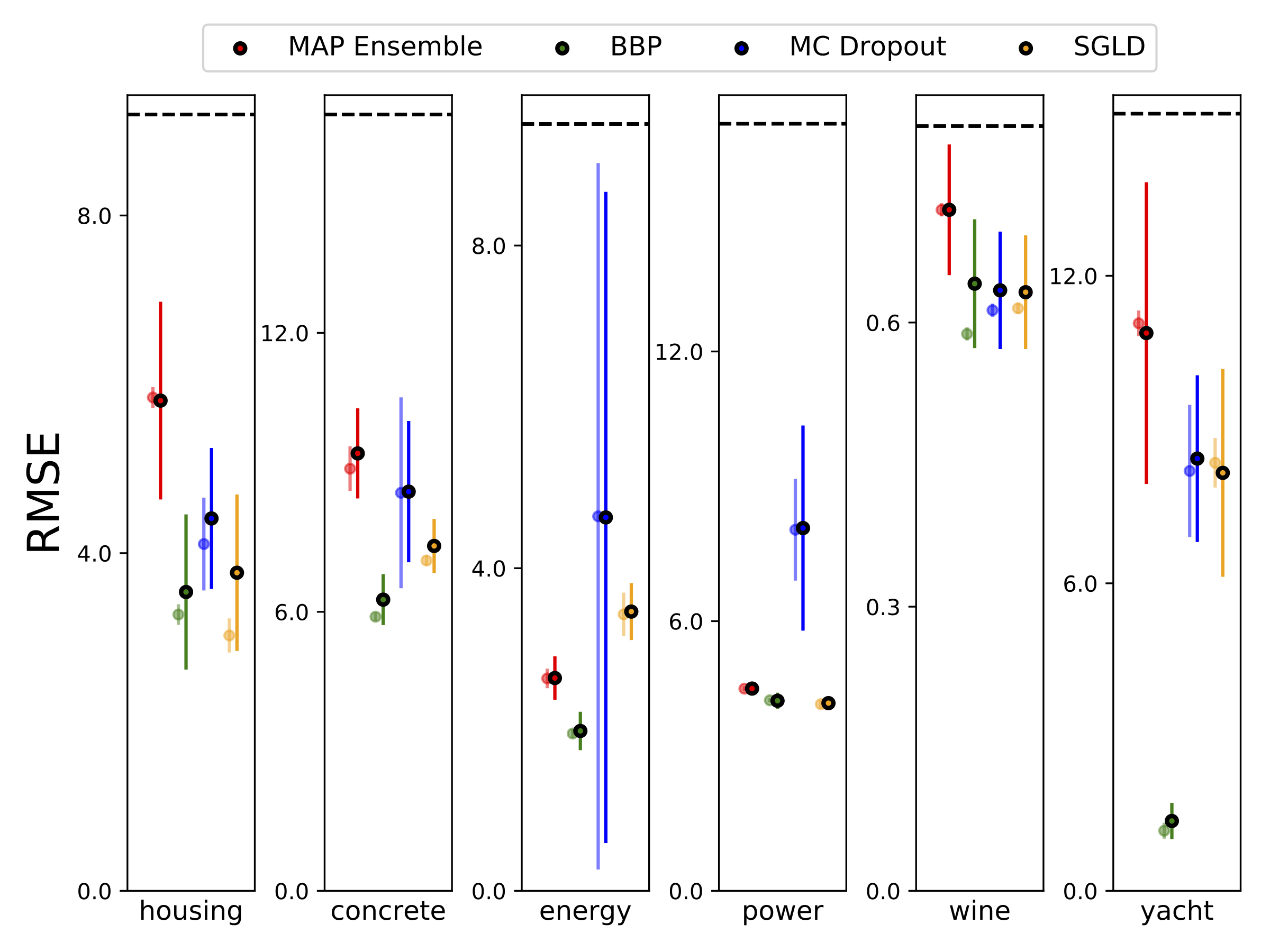
W está marginado con 100 muestras de los pesos para todos los modelos, excepto el mapa, donde solo se usa un conjunto de pesos.
| Prueba de mnist | MAPA | Conjunto de mapa | BBP Gaussian | BBP GMM | BBP Laplace | BBP Local Reparam | Desglose de MC | Sgld | PSGLD |
|---|---|---|---|---|---|---|---|---|---|
| Registrar como | -572.9 | -496.54 | -1100.29 | -1008.28 | -892.85 | -1086.43 | -435.458 | -828.29 | -661.25 |
| Error % | 1.58 | 1.53 | 2.60 | 2.38 | 2.28 | 2.61 | 1.37 | 1.76 | 1.76 |
Resultados de la prueba MNIST para métodos bajo consideración. No se ha realizado un sintonización de hiperparámetro estensivo. Aprovechamos la distribución predictiva posterior con 100 muestras de MC. Utilizamos una red FC con dos capas RELU de 1200 unidades. Si no se especifica, el anterior es gaussiano con STD = 0.1. P-SGLD utiliza preacondicionamiento RMSProp.
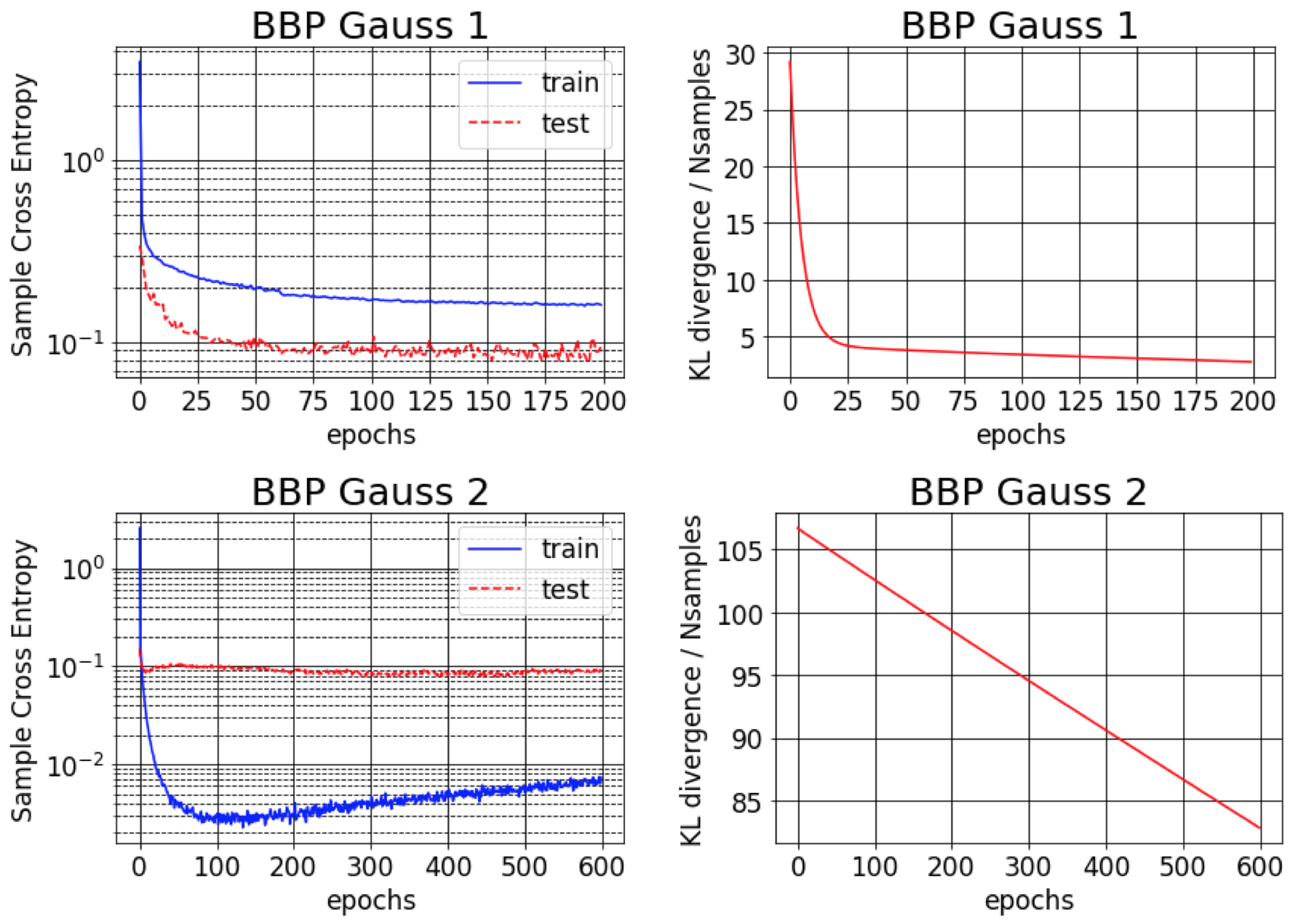
El documento original para Bayes de Backprop informa alrededor del 1% de error en MNIST. Encontramos que este resultado es posible solo si se inicializan las variaciones posteriores aproximadas para ser muy pequeñas (BBP Gauss 2). En este escenario, las distribuciones sobre pesos se asemejan a Deltas, dando un buen rendimiento predictivo pero estimaciones de mala incertidumbre. Sin embargo, al inicializar las variaciones para que coincidan con el anterior (BBP Gauss 1), obtenemos los resultados anteriores. Las curvas de entrenamiento para estos dos esquemas de configuración de hiperparameter se muestran a continuación:
Las incertidumbres totales, aleatóricas y epistémicas obtenidas al crear muestras de OOD aumentando el conjunto de pruebas MNIST con rotaciones:
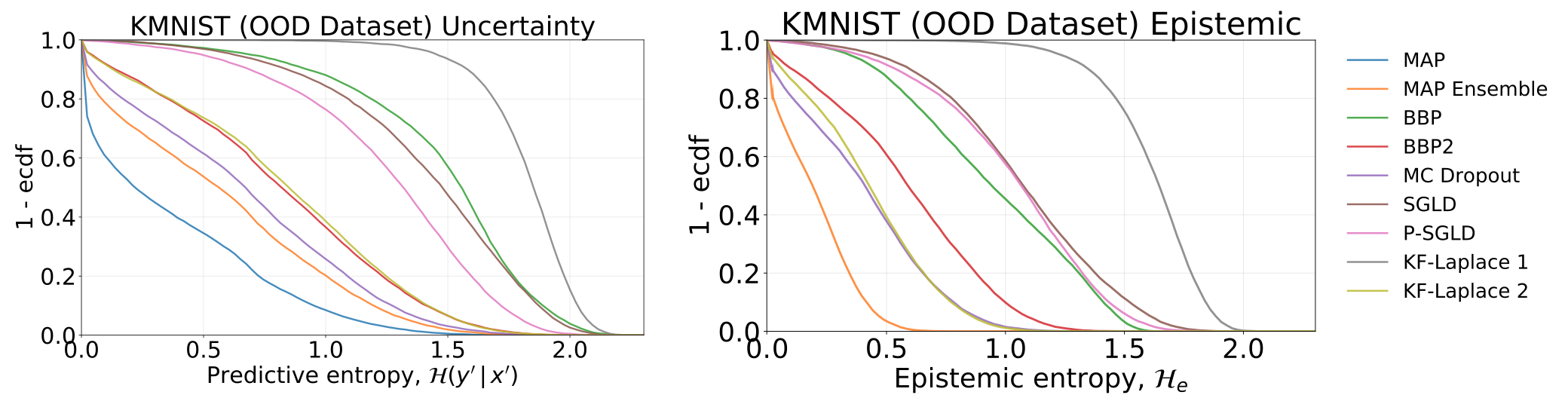
Incertidumbres totales y epistémicas obtenidas al probar nuestros modelos, que han sido capacitados en Mnist, en el conjunto de datos Kmnist:
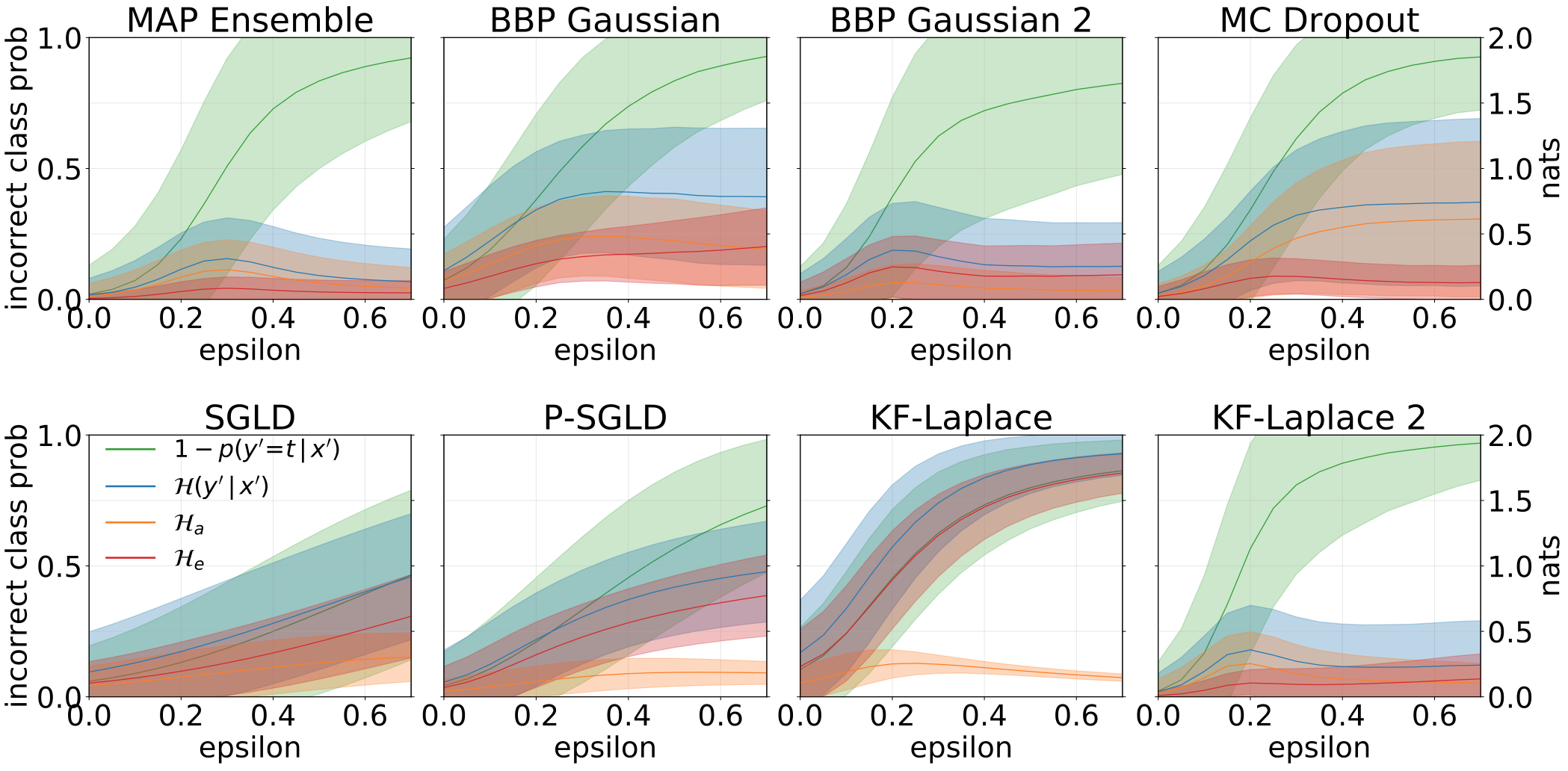
Las incertidumbres totales, aleatóricas y epistémicas obtenidas al alimentar nuestros modelos con muestras adversas (FGSM).
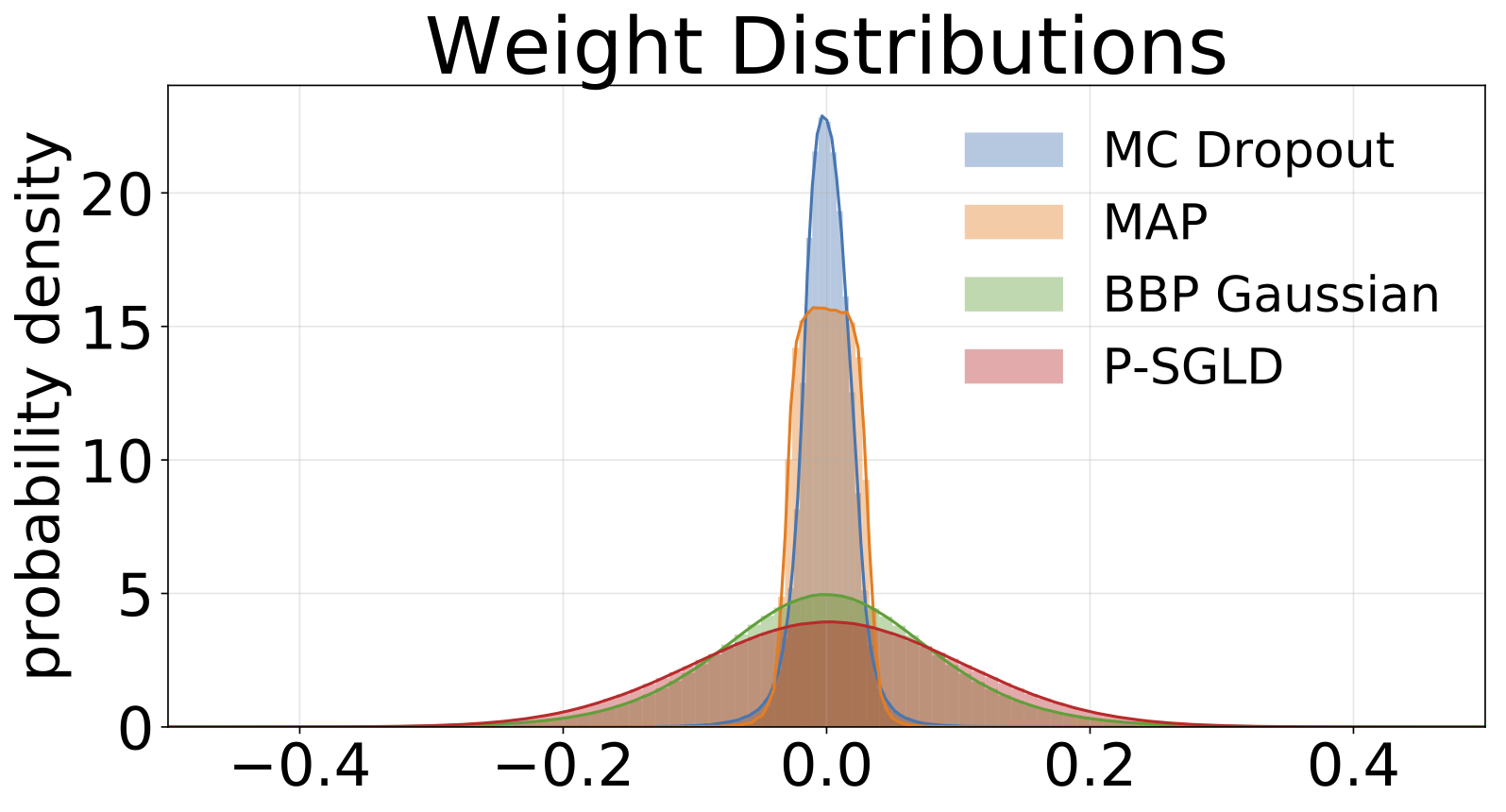
Histogramas de pesos muestreados de cada modelo entrenado en Mnist. Dibujamos 10 muestras de W para cada modelo.
#HACER