Nouvelles: Drunet
Performance de débrassement de pointe
Peut être utilisé pour la restauration d'images plug-and-play

https://github.com/cszn/dpir/blob/master/main_dpir_denizing.py
I recommend to use the PyTorch code for training and testing. The model parameters of MatConvnet and PyTorch are same.
main_train_dncnn.py
main_test_dncnn.py
main_test_dncnn3_deblocking.py
import torch
import torch . nn as nn
def merge_bn ( model ):
''' merge all 'Conv+BN' (or 'TConv+BN') into 'Conv' (or 'TConv')
based on https://github.com/pytorch/pytorch/pull/901
by Kai Zhang ([email protected])
https://github.com/cszn/DnCNN
01/01/2019
'''
prev_m = None
for k , m in list ( model . named_children ()):
if ( isinstance ( m , nn . BatchNorm2d ) or isinstance ( m , nn . BatchNorm1d )) and ( isinstance ( prev_m , nn . Conv2d ) or isinstance ( prev_m , nn . Linear ) or isinstance ( prev_m , nn . ConvTranspose2d )):
w = prev_m . weight . data
if prev_m . bias is None :
zeros = torch . Tensor ( prev_m . out_channels ). zero_ (). type ( w . type ())
prev_m . bias = nn . Parameter ( zeros )
b = prev_m . bias . data
invstd = m . running_var . clone (). add_ ( m . eps ). pow_ ( - 0.5 )
if isinstance ( prev_m , nn . ConvTranspose2d ):
w . mul_ ( invstd . view ( 1 , w . size ( 1 ), 1 , 1 ). expand_as ( w ))
else :
w . mul_ ( invstd . view ( w . size ( 0 ), 1 , 1 , 1 ). expand_as ( w ))
b . add_ ( - m . running_mean ). mul_ ( invstd )
if m . affine :
if isinstance ( prev_m , nn . ConvTranspose2d ):
w . mul_ ( m . weight . data . view ( 1 , w . size ( 1 ), 1 , 1 ). expand_as ( w ))
else :
w . mul_ ( m . weight . data . view ( w . size ( 0 ), 1 , 1 , 1 ). expand_as ( w ))
b . mul_ ( m . weight . data ). add_ ( m . bias . data )
del model . _modules [ k ]
prev_m = m
merge_bn ( m )
def tidy_sequential ( model ):
for k , m in list ( model . named_children ()):
if isinstance ( m , nn . Sequential ):
if m . __len__ () == 1 :
model . _modules [ k ] = m . __getitem__ ( 0 )
tidy_sequential ( m )Version Simplenn
Version dagnn
[Demos] Demo_test_DnCNN-.m
[Modèles] y compris les modèles qualifiés pour le débroussage gaussien; Un modèle unique pour le débroussage gaussien, la super-résolution d'image unique (SISR) et le désobloquerie.
[ensembles de tests] BSD68 et SET10 pour l'évaluation du débrotage gaussien; Ensembles de données SET5, SET14, BSD100 et URBAN100 pour l'évaluation SISR; Classic5 et Live1 pour l'évaluation de la désoblocation de l'image JPEG.
J'ai formé de nouveaux modèles DNCNN flexibles (FDNCNN) basés sur FFDNET.
FDNCNN peut gérer la plage de niveau de bruit de [0, 75] via un seul modèle.
Demo_fdncnn_gray.m
Demo_fdncnn_gray_clip.m
Demo_fdncnn_color.m
Demo_fdncnn_color_clip.m
Architecture de réseau
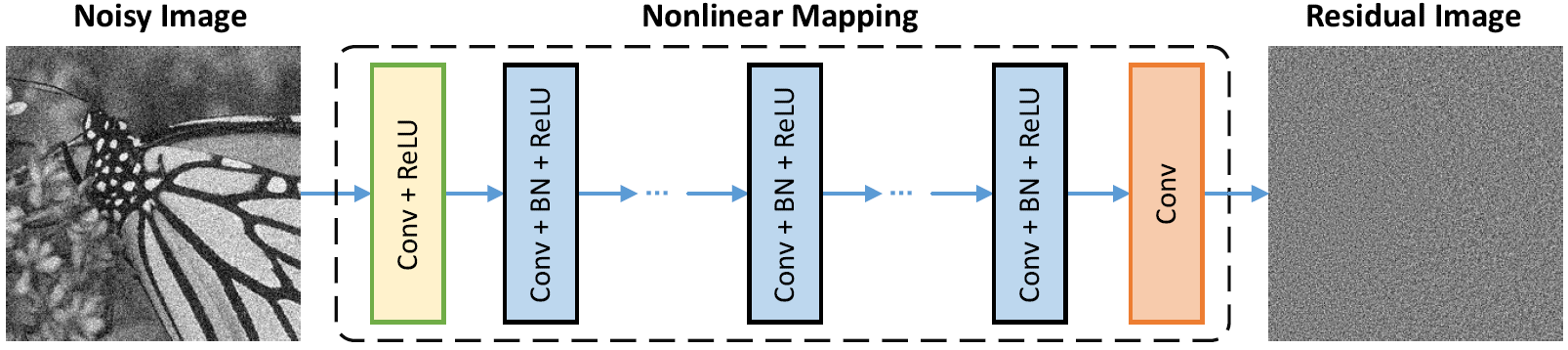
La normalisation par lots et l'apprentissage résiduel sont bénéfiques pour le débraillé gaussien (en particulier pour un seul niveau de bruit). Le résidu d'une image bruyante corrompue par le bruit gaussien blanc additif (AWGN) suit une distribution gaussienne constante qui stablise la normalisation par lots pendant l'entraînement.
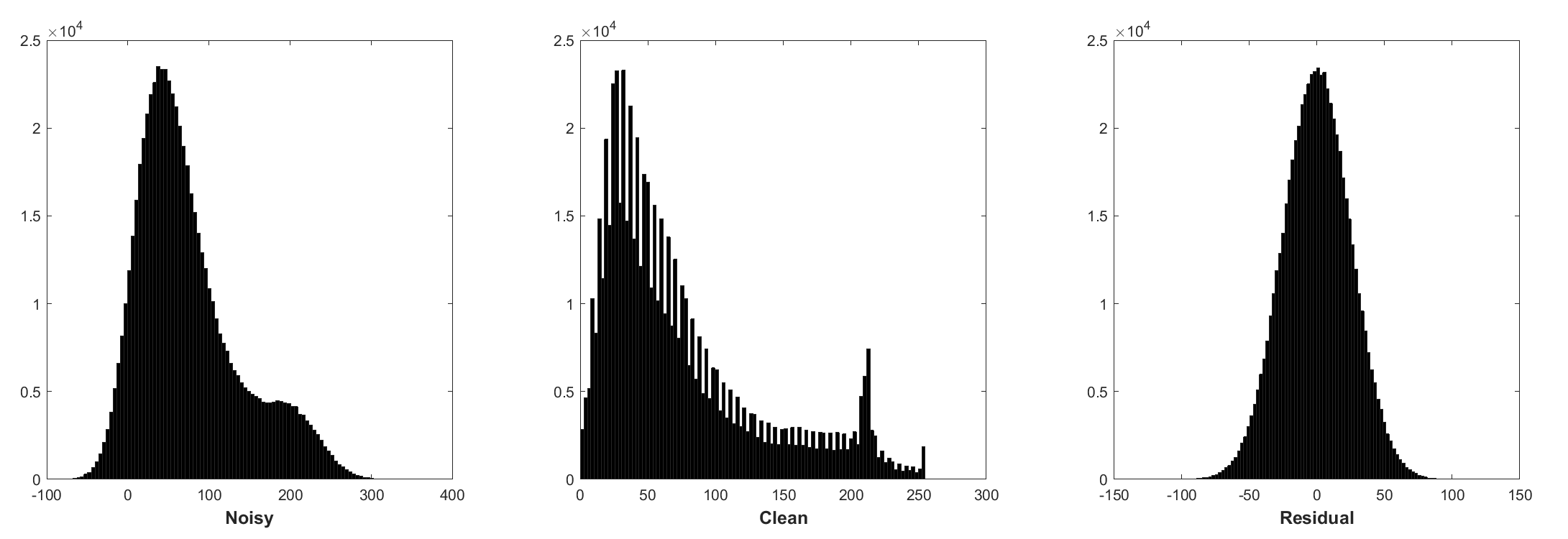
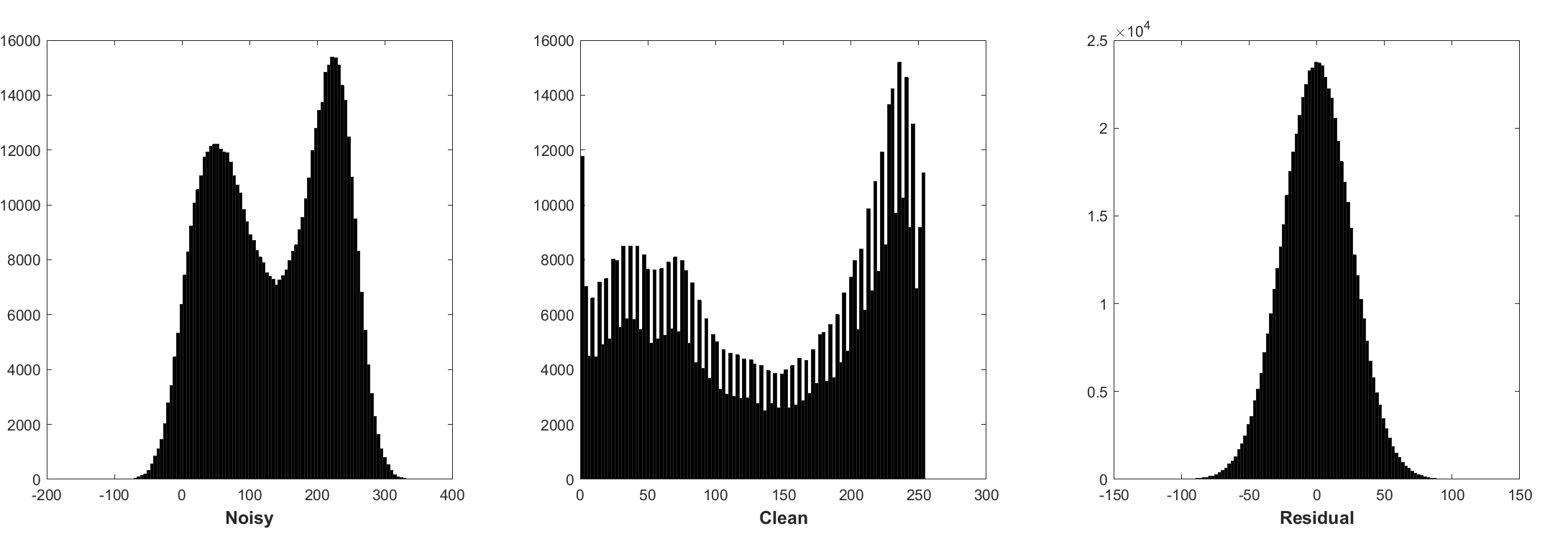
La prévision du résidu peut être interprétée comme effectuant une étape d'inférence de descente à un gradient au point de départ (c'est-à-dire, image bruyante).
Les paramètres dans DNCNN représentent principalement les priors d'image (indépendants des tâches), il est donc possible d'apprendre un modèle unique pour différentes tâches, telles que le débroussage d'image, la super-résolution d'image et le déblocation d'image JPEG.
La gauche est l'image d'entrée corrompue par différentes dégradations, la droite est l'image restaurée par DNCNN-3.


Les résultats PSNR (DB) moyens de différentes méthodes sur l'ensemble de données BSD68.
| Niveau de bruit | BM3d | Wnnm | EPLL | MLP | CSF | Tnrd | Dncnn | Dncnn-b | Fdncnn | Ruisseau |
|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 31.07 | 31.37 | 31.21 | - | 31.24 | 31.42 | 31.73 | 31.61 | 31.69 | 31.91 |
| 25 | 28.57 | 28.83 | 28.68 | 28.96 | 28.74 | 28.92 | 29.23 | 29.16 | 29.22 | 29.48 |
| 50 | 25,62 | 25.87 | 25.67 | 26.03 | - | 25.97 | 26.23 | 26.23 | 26.27 | 26.59 |
Résultats visuels
La gauche est l'image bruyante corrompue par AWGN, le milieu est l'image déborde par Dncnn, la droite est la truth au sol.









Résultats moyens PSNR (DB) / SSIM de différentes méthodes pour le débroussage gaussien avec le niveau de bruit 15, 25 et 50 sur le jeu de données BSD68, la super-résolution d'image unique avec des facteurs de mise à l'échelle 2, 3 et 40 sur SET5, SET14, BSD100 et Urban100 DataSets, JPEG Image DeBlocks avec des facteurs de qualité 10, 20, 30 et 40 sur Classic5 et Live11 Dataset.
| Ensemble de données | Niveau de bruit | BM3d | Tnrd | DNCNN-3 |
|---|---|---|---|---|
| 15 | 31.08 / 0.8722 | 31,42 / 0.8826 | 31,46 / 0,8826 | |
| BSD68 | 25 | 28,57 / 0,8017 | 28,92 / 0,8157 | 29.02 / 0.8190 |
| 50 | 25,62 / 0,6869 | 25,97 / 0,7029 | 26.10 / 0.7076 |
| Ensemble de données | Facteur de mise à l'échelle | Tnrd | Vdsr | DNCNN-3 |
|---|---|---|---|---|
| 2 | 36,86 / 0,9556 | 37,56 / 0,9591 | 37,58 / 0.9590 | |
| Set5 | 3 | 33,18 / 0.9152 | 33,67 / 0,9220 | 33,75 / 0,9222 |
| 4 | 30,85 / 0,8732 | 31,35 / 0.8845 | 31,40 / 0.8845 | |
| 2 | 32,51 / 0.9069 | 33,02 / 0.9128 | 33,03 / 0.9128 | |
| Set14 | 3 | 29,43 / 0,8232 | 29,77 / 0,8318 | 29,81 / 0.8321 |
| 4 | 27,66 / 0,7563 | 27,99 / 0,7659 | 28.04 / 0.7672 | |
| 2 | 31,40 / 0.8878 | 31,89 / 0.8961 | 31,90 / 0.8961 | |
| BSD100 | 3 | 28,50 / 0,7881 | 28,82 / 0.7980 | 28,85 / 0,7981 |
| 4 | 27.00 / 0.7140 | 27,28 / 0,7256 | 27.29 / 0.7253 | |
| 2 | 29,70 / 0.8994 | 30,76 / 0,9143 | 30,74 / 0.9139 | |
| Urbain100 | 3 | 26,42 / 0,8076 | 27.13 / 0.8283 | 27.15 / 0.8276 |
| 4 | 24,61 / 0.7291 | 25.17 / 0.7528 | 25,20 / 0,7521 |
| Ensemble de données | Facteur de qualité | AR-CNN | Tnrd | DNCNN-3 |
|---|---|---|---|---|
| Classique5 | 10 | 29.03 / 0.7929 | 29.28 / 0.7992 | 29.40 / 0.8026 |
| 20 | 31.15 / 0.8517 | 31,47 / 0,8576 | 31,63 / 0.8610 | |
| 30 | 32,51 / 0.8806 | 32,78 / 0,8837 | 32,91 / 0.8861 | |
| 40 | 33,34 / 0,8953 | - | 33,77 / 0,9003 | |
| Live1 | 10 | 28,96 / 0,8076 | 29.15 / 0.8111 | 29.19 / 0.8123 |
| 20 | 31.29 / 0.8733 | 31,46 / 0.8769 | 31,59 / 0,8802 | |
| 30 | 32,67 / 0,9043 | 32,84 / 0,9059 | 32,98 / 0.9090 | |
| 40 | 33,63 / 0,9198 | - | 33,96 / 0,9247 |
Ou simplement MATLAB R2015B pour tester le modèle.
Dncnn / demo_test_dncnn.m
Lignes 64 à 65 en 4A4B5B8
@article { zhang2017beyond ,
title = { Beyond a {Gaussian} denoiser: Residual learning of deep {CNN} for image denoising } ,
author = { Zhang, Kai and Zuo, Wangmeng and Chen, Yunjin and Meng, Deyu and Zhang, Lei } ,
journal = { IEEE Transactions on Image Processing } ,
year = { 2017 } ,
volume = { 26 } ,
number = { 7 } ,
pages = { 3142-3155 } ,
}
@article { zhang2020plug ,
title = { Plug-and-Play Image Restoration with Deep Denoiser Prior } ,
author = { Zhang, Kai and Li, Yawei and Zuo, Wangmeng and Zhang, Lei and Van Gool, Luc and Timofte, Radu } ,
journal = { arXiv preprint } ,
year = { 2020 }
}===========================================================.
@Inbook{zuo2018convolutional,
author={Zuo, Wangmeng and Zhang, Kai and Zhang, Lei},
editor={Bertalm{'i}o, Marcelo},
title={Convolutional Neural Networks for Image Denoising and Restoration},
bookTitle={Denoising of Photographic Images and Video: Fundamentals, Open Challenges and New Trends},
year={2018},
publisher={Springer International Publishing},
address={Cham},
pages={93--123},
isbn={978-3-319-96029-6},
doi={10.1007/978-3-319-96029-6_4},
url={https://doi.org/10.1007/978-3-319-96029-6_4}
}
Bien que le dénaison d'image pour la suppression d'AWGN ait été bien étudié, peu de travail a été effectué sur le débroussage réel de l'image. La principale difficulté résulte du fait que les bruits réels sont beaucoup plus complexes que AWGN et qu'il n'est pas facile d'évaluer soigneusement les performances d'un Dencher. La figure 4.15 montre quatre types de bruit typiques dans le monde réel. On peut voir que les caractéristiques de ces bruits sont très différentes et qu'un seul niveau de bruit peut ne pas être suffisant pour paramétrer ces types de bruit. Dans la plupart des cas, un Denoisi ne peut bien fonctionner que sous un certain modèle de bruit. Par exemple, un modèle de débraillé formé pour l'élimination de l'AWGN n'est pas efficace pour l'élimination du bruit gaussien mixte et de Poisson. Ceci est intuitivement raisonnable car les méthodes basées sur CNN peuvent être traitées comme un cas général de l'équation. (4.3) et le terme de fidélité des données important correspond au processus de dégradation. En dépit de cela, le débroussage de l'image pour la suppression de l'AWGN est précieux pour les raisons suivantes. Premièrement, il s'agit d'un banc d'essai idéal pour évaluer l'efficacité de différentes méthodes de débraillage basées sur CNN. Deuxièmement, dans l'inférence déroulée via des techniques de division variable, de nombreux problèmes de restauration d'images peuvent être résolus en résolvant séquentiellement une série de sous-problèmes de débraillage gaussien, qui élargissent encore les champs d'application.

Pour améliorer la praticabilité d'un CNN Denoisever, le moyen le plus simple est peut-être de capturer des quantités adéquates de véritables paires d'entraînement bruyantes pour la formation afin que le véritable espace de dégradation puisse être couvert. Cette solution a un avantage qu'il n'est pas nécessaire de connaître le processus de dégradation complexe. Cependant, la dérivation de l'image propre correspondante d'un bruyant n'est pas une tâche triviale en raison de la nécessité d'étapes prudentes de post-traitement, telles que l'alignement spatial et la correction de l'éclairage. Alternativement, on peut simuler le processus de dégradation réel pour synthétiser des images bruyantes pour une propreté. Cependant, il n'est pas facile de modéliser avec précision le processus de dégradation complexe. En particulier, le modèle de bruit peut être différent dans différentes caméras. Néanmoins, il est pratiquement préférable de modéliser à peu près un certain type de bruit pour la formation, puis d'utiliser le modèle CNN appris pour le débrage spécifique au type.
Outre les données de formation, l'architecture robuste et la formation robuste jouent également des rôles essentiels pour le succès d'un Denoisiment CNN. Pour l'architecture robuste, la conception d'un CNN multi-échelle profond qui implique une procédure grossière à la fin est une direction prometteuse. Un tel réseau devrait hériter des mérites de plusieurs échelles: (i) le niveau de bruit diminue à des échelles plus grandes; (ii) le bruit à basse fréquence omniprésent peut être atténué par la procédure à plusieurs échelles; et (iii) la réduction de l'image avant le débroussage peut effectivement agrandir le classé réceptif. Pour la formation robuste, l'efficacité du Denoisi formé avec des réseaux adversaires génératifs (GAN) pour le débroussage réel de l'image reste encore plus approfondie. L'idée principale du débrage à base de GAN est d'introduire une perte contradictoire pour améliorer la qualité perceptuelle de l'image déborde. En outre, un avantage distinctif de Gan est qu'il peut faire un apprentissage non supervisé. Plus précisément, l'image bruyante sans vérité au sol peut être utilisée dans la formation. Jusqu'à présent, nous avons fourni plusieurs solutions possibles pour améliorer la praticabilité d'un Denoisi CNN. Nous devons noter que ces solutions peuvent être combinées pour améliorer encore les performances.