Inicio>Relacionado con la programación>Pitón
Descargar

Dncnn

Más allá de un denoiser gaussiano: aprendizaje residual de CNN profunda para la renovación de imágenes

Noticias: Drunet

  • Rendimiento de descenso de última generación

  • Se puede usar para la restauración de imágenes con plug-and-play

  • https://github.com/cszn/dpir/blob/master/main_dpir_denoising.py

Código de entrenamiento y prueba de Pytorch - 18/12/2019

I recommend to use the PyTorch code for training and testing. The model parameters of MatConvnet and PyTorch are same.

  • main_train_dncnn.py

  • main_test_dncnn.py

  • main_test_dncnn3_deblowing.py

Fusionar la normalización por lotes (Pytorch) 

 import torch
import torch . nn as nn


def merge_bn ( model ):
    ''' merge all 'Conv+BN' (or 'TConv+BN') into 'Conv' (or 'TConv')
    based on https://github.com/pytorch/pytorch/pull/901
    by Kai Zhang ([email protected]) 
    https://github.com/cszn/DnCNN
    01/01/2019
    '''
    prev_m = None
    for k , m in list ( model . named_children ()):
        if ( isinstance ( m , nn . BatchNorm2d ) or isinstance ( m , nn . BatchNorm1d )) and ( isinstance ( prev_m , nn . Conv2d ) or isinstance ( prev_m , nn . Linear ) or isinstance ( prev_m , nn . ConvTranspose2d )):

            w = prev_m . weight . data

            if prev_m . bias is None :
                zeros = torch . Tensor ( prev_m . out_channels ). zero_ (). type ( w . type ())
                prev_m . bias = nn . Parameter ( zeros )
            b = prev_m . bias . data

            invstd = m . running_var . clone (). add_ ( m . eps ). pow_ ( - 0.5 )
            if isinstance ( prev_m , nn . ConvTranspose2d ):
                w . mul_ ( invstd . view ( 1 , w . size ( 1 ), 1 , 1 ). expand_as ( w ))
            else :
                w . mul_ ( invstd . view ( w . size ( 0 ), 1 , 1 , 1 ). expand_as ( w ))
            b . add_ ( - m . running_mean ). mul_ ( invstd )
            if m . affine :
                if isinstance ( prev_m , nn . ConvTranspose2d ):
                    w . mul_ ( m . weight . data . view ( 1 , w . size ( 1 ), 1 , 1 ). expand_as ( w ))
                else :
                    w . mul_ ( m . weight . data . view ( w . size ( 0 ), 1 , 1 , 1 ). expand_as ( w ))
                b . mul_ ( m . weight . data ). add_ ( m . bias . data )

            del model . _modules [ k ]
        prev_m = m
        merge_bn ( m )


def tidy_sequential ( model ):
    for k , m in list ( model . named_children ()):
        if isinstance ( m , nn . Sequential ):
            if m . __len__ () == 1 :
                model . _modules [ k ] = m . __getitem__ ( 0 )
        tidy_sequential ( m )

Entrenamiento (Matconvnet)

  • Versión simple

    • Dncnn_trainingcodes_v1.1

  • Versión de Dagnn

    • Dncnn_trainingcodes_dagnn_v1.1

Prueba (MatConvnet o Matlab)

  • [Demos] Demo_test_DnCNN-.m .

  • [modelos] incluyendo los modelos entrenados para la renovación gaussiana; Un solo modelo para la denoización gaussiana, la super resolución de una sola imagen (SISR) y el desbloqueo.

  • [TestSets] BSD68 y SET10 para la evaluación gaussiana de desociones; SET5, SET14, BSD100 y URBAN100 DATASTS conjuntos para evaluación SISR; Classic5 y Live1 para JPEG Image Desbloking Evaluation.

Nuevos modelos FDNCNN

He entrenado nuevos modelos DNCNN (FDNCNN) flexibles basados ​​en FFDNET.

FDNCNN puede manejar el rango de nivel de ruido de [0, 75] a través de un solo modelo.

Demo_fdncnn_gray.m

Demo_fdncnn_gray_clip.m

Demo_fdncnn_color.m

Demo_fdncnn_color_clip.m

Arquitectura de red y lápidas de diseño

  • Arquitectura de red

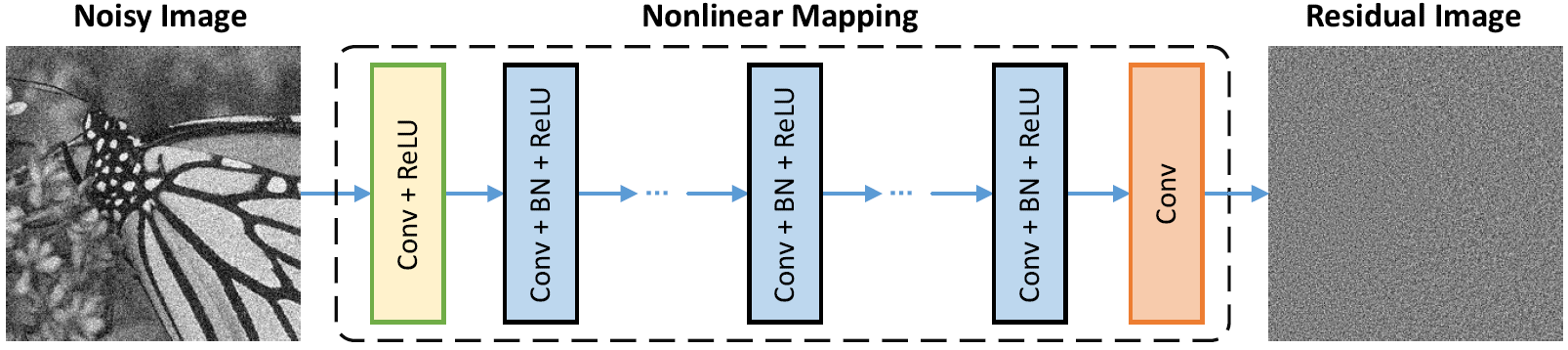
  • La normalización por lotes y el aprendizaje residual son beneficiosos para la renovación gaussiana (especialmente para un solo nivel de ruido). El residuo de una imagen ruidosa corrompida por el ruido gaussiano blanco aditivo (AWGN) sigue una distribución gaussiana constante que estabiliza la normalización por lotes durante el entrenamiento.

    • Histograma de parches ruidosos, parches limpios y parches residuales (ruido) de un lote de entrenamiento. El nivel de ruido es 25, el tamaño del parche es 40x40, el tamaño de lote es 128.
    • Histograma de parches ruidosos, parches limpios y parches residuales (ruido) de otro lote de entrenamiento. El nivel de ruido es 25, el tamaño del parche es 40x40, el tamaño de lote es 128.
    • La super-resolución de imagen libre de ruido no tiene esta propiedad.

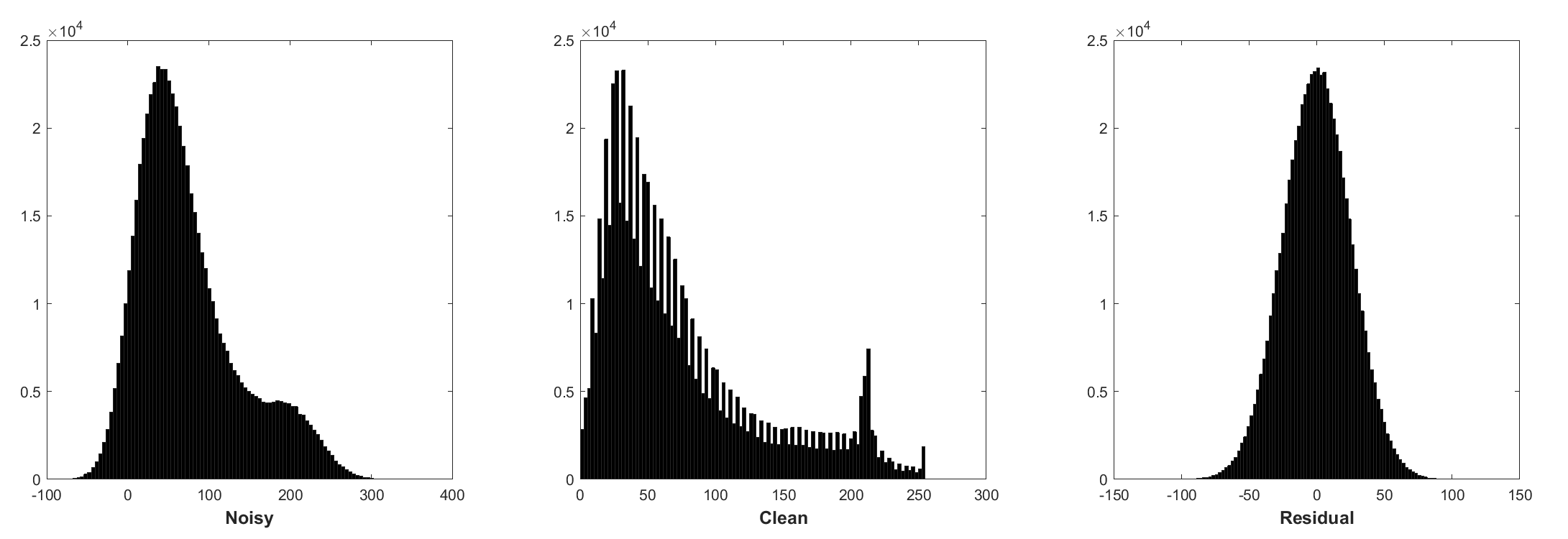
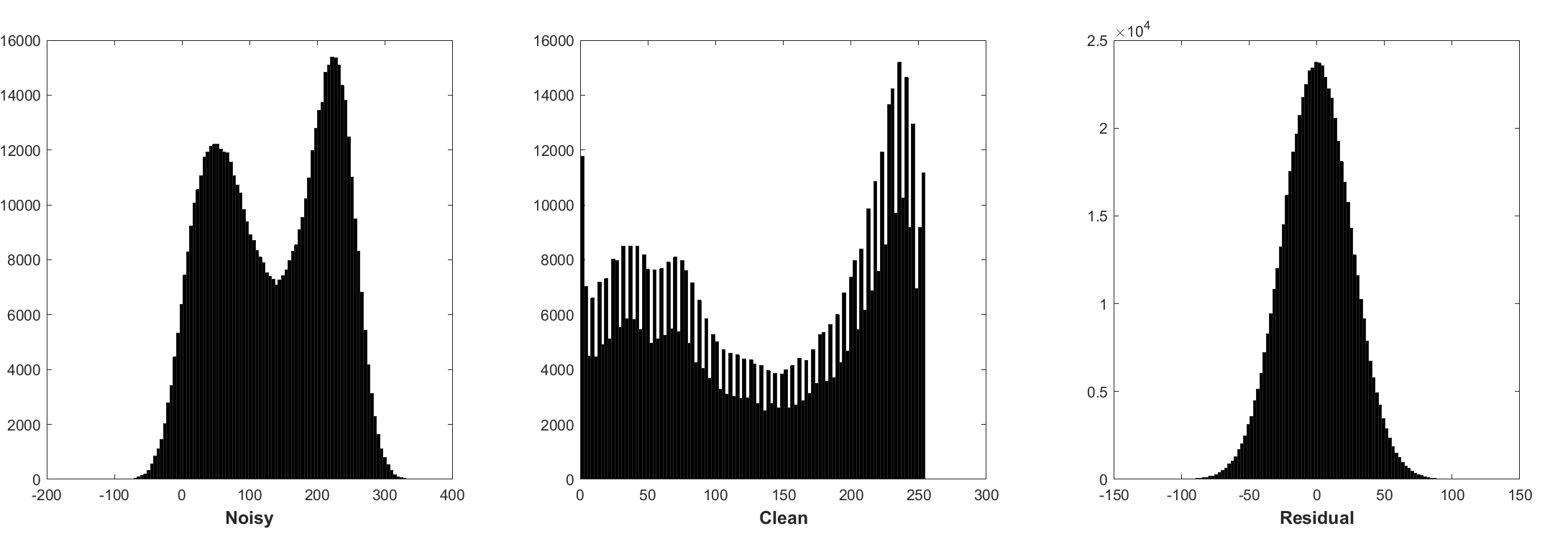
  • La predicción del residual puede interpretarse como una realización de inferencia de descenso de gradiente en el punto de partida (es decir, imagen ruidosa).

    • Los parámetros en DNCNN representan principalmente los antecedentes de la imagen (independientes de la tarea), por lo tanto, es posible aprender un modelo único para diferentes tareas, como la cenanización de imágenes, la súper resolución de la imagen y el desbloqueo de imágenes JPEG.

    • La izquierda es la imagen de entrada corrompida por diferentes degradaciones, la derecha es la imagen restaurada por DNCNN-3.

Resultados

Denoiseing gaussiano

Los resultados promedio de PSNR (DB) de diferentes métodos en el conjunto de datos BSD68.

Nivel de ruido BM3D WNNM EPLL MLP CSF TNRD Dncnn Dncnn-b Fdncnn Drunet
15 31.07 31.37 31.21 - 31.24 31.42 31.73 31.61 31.69 31.91
25 28.57 28.83 28.68 28.96 28.74 28.92 29.23 29.16 29.22 29.48
50 25.62 25.87 25.67 26.03 - 25.97 26.23 26.23 26.27 26.59

Resultados visuales

La izquierda es la imagen ruidosa corrompida por AWGN, el medio es la imagen denocada de DNCNN, la derecha es la verdad en tierra.

Denoising Gaussian, resolución de imágenes individuales y JPEG Image Desblocking a través de un solo modelo (DNCNN-3)

Resultados promedio de PSNR (DB)/SSIM de diferentes métodos para la renovación gaussiana con el nivel de ruido 15, 25 y 50 en el conjunto de datos BSD68, la súper resolución de la imagen única con factores de escala 2, 3 y 40 en SET5, SET14, BSD100 y conjuntos de datos Urban100, imagen de imagen JPEG con factores de calidad 10, 20 y 40 en los datos clásicos de clásicos5 y vivos11.

Denoiseing gaussiano

Conjunto de datos Nivel de ruido BM3D TNRD DNCNN-3
15 31.08 / 0.8722 31.42 / 0.8826 31.46 / 0.8826
BSD68 25 28.57 / 0.8017 28.92 / 0.8157 29.02 / 0.8190
50 25.62 / 0.6869 25.97 / 0.7029 26.10 / 0.7076

SUGEN SUPER SUPERROLUCIÓN

Conjunto de datos Factor de mejora TNRD VDSR DNCNN-3
2 36.86 / 0.9556 37.56 / 0.9591 37.58 / 0.9590
Set5 3 33.18 / 0.9152 33.67 / 0.9220 33.75 / 0.9222
4 30.85 / 0.8732 31.35 / 0.8845 31.40 / 0.8845
2 32.51 / 0.9069 33.02 / 0.9128 33.03 / 0.9128
Set14 3 29.43 / 0.8232 29.77 / 0.8318 29.81 / 0.8321
4 27.66 / 0.7563 27.99 / 0.7659 28.04 / 0.7672
2 31.40 / 0.8878 31.89 / 0.8961 31.90 / 0.8961
BSD100 3 28.50 / 0.7881 28.82 / 0.7980 28.85 / 0.7981
4 27.00 / 0.7140 27.28 / 0.7256 27.29 / 0.7253
2 29.70 / 0.8994 30.76 / 0.9143 30.74 / 0.9139
Urbano100 3 26.42 / 0.8076 27.13 / 0.8283 27.15 / 0.8276
4 24.61 / 0.7291 25.17 / 0.7528 25.20 / 0.7521

Desbloqueo de imágenes JPEG

Conjunto de datos Factor de calidad AR-CNN TNRD DNCNN-3
Classic5 10 29.03 / 0.7929 29.28 / 0.7992 29.40 / 0.8026
20 31.15 / 0.8517 31.47 / 0.8576 31.63 / 0.8610
30 32.51 / 0.8806 32.78 / 0.8837 32.91 / 0.8861
40 33.34 / 0.8953 - 33.77 / 0.9003
Live1 10 28.96 / 0.8076 29.15 / 0.8111 29.19 / 0.8123
20 31.29 / 0.8733 31.46 / 0.8769 31.59 / 0.8802
30 32.67 / 0.9043 32.84 / 0.9059 32.98 / 0.9090
40 33.63 / 0.9198 - 33.96 / 0.9247

Requisitos y dependencias

  • MATLAB R2015B
  • CUDA-8.0 y CUDNN V-5.1
  • Matconvnet

O simplemente MATLAB R2015B para probar el modelo.

Dncnn/demo_test_dncnn.m

Líneas 64 a 65 en 4A4B5B8

res = vl_simplenn ( net , input , [], [], ' ConservemEmemory ' , verdadero , ' Modo ' , ' Test ' );
% res = simplenn_matlab (net, entrada); %%% Use esto si no instaló MatConvnet.

Citación 

 @article { zhang2017beyond ,
  title = { Beyond a {Gaussian} denoiser: Residual learning of deep {CNN} for image denoising } ,
  author = { Zhang, Kai and Zuo, Wangmeng and Chen, Yunjin and Meng, Deyu and Zhang, Lei } ,
  journal = { IEEE Transactions on Image Processing } ,
  year = { 2017 } ,
  volume = { 26 } , 
  number = { 7 } , 
  pages = { 3142-3155 } , 
}
@article { zhang2020plug ,
  title = { Plug-and-Play Image Restoration with Deep Denoiser Prior } ,
  author = { Zhang, Kai and Li, Yawei and Zuo, Wangmeng and Zhang, Lei and Van Gool, Luc and Timofte, Radu } ,
  journal = { arXiv preprint } ,
  year = { 2020 }
}

=========================================================================================================

Redes neuronales convolucionales para la rango y restauración de imágenes 

 @Inbook{zuo2018convolutional,
author={Zuo, Wangmeng and Zhang, Kai and Zhang, Lei},
editor={Bertalm{'i}o, Marcelo},
title={Convolutional Neural Networks for Image Denoising and Restoration},
bookTitle={Denoising of Photographic Images and Video: Fundamentals, Open Challenges and New Trends},
year={2018},
publisher={Springer International Publishing},
address={Cham},
pages={93--123},
isbn={978-3-319-96029-6},
doi={10.1007/978-3-319-96029-6_4},
url={https://doi.org/10.1007/978-3-319-96029-6_4}
}

Desafíos y posibles soluciones (del capítulo del libro anterior)

Si bien la imagen de la eliminación de la imagen para la eliminación de AWGN ha sido bien estudiada, se ha trabajado poco en la renovación de imágenes reales. La principal dificultad surge del hecho de que los ruidos reales son mucho más complejos que AWGN y no es una tarea fácil evaluar a fondo el rendimiento de un Denoiser. La figura 4.15 muestra cuatro tipos de ruido típicos en el mundo real. Se puede ver que las características de esos ruidos son muy diferentes y un solo nivel de ruido puede no ser suficiente para parametrizar esos tipos de ruido. En la mayoría de los casos, un Denoiser solo puede funcionar bien bajo un cierto modelo de ruido. Por ejemplo, un modelo de renovación entrenado para la eliminación de AWGN no es efectivo para la eliminación de ruido de Gausson y Poisson mixto. Esto es intuitivamente razonable porque los métodos basados ​​en CNN pueden tratarse como un caso general de la ecuación. (4.3) y el importante término de fidelidad de datos corresponde al proceso de degradación. A pesar de esto, la imagen que se deneización para la eliminación de AWGN es valiosa debido a las siguientes razones. Primero, es un lecho de prueba ideal para evaluar la efectividad de los diferentes métodos de renovación basados ​​en CNN. En segundo lugar, en la inferencia desenrollada a través de técnicas de división variable, se pueden abordar muchos problemas de restauración de imágenes resolviendo secuencialmente una serie de subproblemas de renovación gaussiana, que amplía aún más los campos de aplicación.

Para mejorar la práctica de un Denoiser de CNN, quizás la forma más directa es capturar cantidades adecuadas de pares de entrenamiento ruidosos reales para el entrenamiento para que el espacio de degradación real pueda estar cubierto. Esta solución tiene la ventaja de que no hay necesidad de conocer el complejo proceso de degradación. Sin embargo, derivar la imagen limpia correspondiente de una ruidosa no es una tarea trivial debido a la necesidad de cuidadosos pasos posteriores al procesamiento, como la alineación espacial y la corrección de iluminación. Alternativamente, se puede simular el proceso de degradación real para sintetizar imágenes ruidosas para una limpia. Sin embargo, no es fácil modelar con precisión el proceso de degradación complejo. En particular, el modelo de ruido puede ser diferente en diferentes cámaras. Sin embargo, es prácticamente preferible modelar aproximadamente un cierto tipo de ruido para el entrenamiento y luego usar el modelo CNN aprendido para la renovación específica de tipo.

Además de los datos de capacitación, la arquitectura robusta y la capacitación robusta también juegan roles vitales para el éxito de un Denoiser de CNN. Para la arquitectura robusta, diseñar un CNN multiescala profundo que implica un procedimiento grueso a fines es una dirección prometedora. Se espera que dicha red hereda los méritos de la multiescala: (i) el nivel de ruido disminuye a escalas más grandes; (ii) el ruido ubicuo de baja frecuencia puede aliviarse mediante procedimiento multiescala; y (iii) reducción de muestras de la imagen antes de la renovación puede ampliar efectivamente el receptivo archivado. Para la sólida capacitación, la efectividad del Denoiser entrenado con redes adversas generativas (GaN) para la renovación de imágenes reales sigue siendo una mayor investigación. La idea principal de Denoising basado en GaN es introducir una pérdida de adversaria para mejorar la calidad perceptiva de la imagen de Denoiseed. Además, una ventaja distintiva de GaN es que puede hacer un aprendizaje sin supervisión. Más específicamente, la imagen ruidosa sin verdad en tierra se puede usar en el entrenamiento. Hasta ahora, hemos proporcionado varias soluciones posibles para mejorar la práctica de un Denoiser CNN. Debemos tener en cuenta que esas soluciones se pueden combinar para mejorar aún más el rendimiento.

Expandir
Información adicional
Aplicaciones relacionadas
Recomendado para ti
Información relacionada Todo