Neslib.MultipRecision添加了另外两种供Delphi使用的浮点类型。这些提供的精度最高4倍,比Double类型的精度高4倍。
Neslib.MultipRecision建立在QD 2.3.22之上,并在以下操作:
用于这些类型的算法是由David H. Bailey,Yozo Hida和Xiaoye S. Li开发的。如果您对详细信息感兴趣,请查看C子目录中的QD.pdf文件。
安装:
> git clone https://github.com/neslib/Neslib.MultiPrecision该库对其他库没有依赖性。也没有运行时间依赖性。使用对象文件或静态库将基础C/C ++ QD库链接到可执行文件中。
该库定义了另外两种浮点类型:
DoubleDouble :这是一种128位类型,其精度是Double类型的两倍。QuadDouble :这是一种256位类型,其精度是Double类型的四倍。两种类型的范围与双重类型相同(大约±10 308 ),但精度更高。与Single和Double相比:
| 类型 | 指数 位 | 尾数 位 | 精确 (十进制数字) |
|---|---|---|---|
| 单身的 | 9 | 24 | 7 |
| 双倍的 | 12 | 53 | 16 |
| doubleduble | 12 | 106 | 32 |
| QuadDouble | 12 | 212 | 64 |
名称
DoubleDouble和QuadDouble来自基础QD库。我考虑使用这些Float128和Float256命名,但是已经有针对此类(硬件)类型的官方IEEE规格。而且由于这些与DoubleDouble和QuadDouble不兼容,所以我不想增加混乱。
基础QD库不使用仿真来计算。取而代之的是,它使用CPU的现有浮点功能使用2或4个Double值来提高精度。结果,这些类型的速度比使用相同精度的其他任意/高精度数学库快得多。同样,与许多其他库相反,这些类型不需要动态内存分配,这进一步有助于性能并减少记忆力碎片。
DoubleDouble和QuadDouble类型的使用方式与Double类型大致相同。他们支持通常的操作员( + , - , * , / , = , <> , < , <= , >和>= ),以及可用于Double类型的记录助手( IsNan , IsInfinity ,isInfinity,isnegatientInfinity, IsNegativeInfinity ,IseponiverInfinity,ispostiveinfinity,tostring, IsPositiveInfinity , ToString , Parse和TryParse )。有一些方法和运算符可以转换为Double , DoubleDouble , QuadDouble和String 。
由于Delphi语言不允许您在源代码中输入高精度浮点文字,因此必须以其他方式初始化DoubleDouble或QuadDouble变量的值。有多种选项(假设DD在此处类型为DoubleDouble ):
Init过载之一。例如, DD.Init(1.23);初始化Double的DoubleDouble 。DD := DoubleDouble(1.23); 。DD := DoubleDouble.Pi; 。DD := '3.1415926535897932384626433832795'; 。我没有添加隐式运算符,例如
DD := 1.23;,由于这些可能导致无意的转换会影响性能。
在执行任何DoubleDouble / QuadDouble计算之前,您必须调用MultiPrecisionInit 。这为高精度数学准备了FPU/CPU。您可以使用MultiPrecisionReset将FPU/CPU恢复为先前的状态。
库的默认配置适用于大多数应用程序。这种配置为提高速度而牺牲了一些精度。如果出于您的目的,精度比速度更重要,则可以使用MP_ACCURATE定义编译库。这将使许多计算更慢,但更准确。
基础QD库(以及此库)支持各种常见的数学函数。此外,neslib.MultipRecision库增加了系统中发现的功能的许多等效物。系统性和系统。
| 姓名 | 描述 |
|---|---|
| strtodoubeduble,strtoquadduble, strtodoubledef,strtoquaddoubledef, Trystrtofloat | 转换为字符串 |
| floattostr,floattostrf | 转换为字符串 |
| 逆 | 计算倒数 |
| REM | 计算剩余,四舍五入到最近 |
| Divrem | 计算划分的结果,包括剩余 |
| fmod | 计算剩余,朝零舍入 |
| SQRT,SQR | 平方根和正方形 |
| 毛,地板,天花板,圆形 | 各种舍入方法 |
| 腹肌 | 绝对值 |
| 最小值 | 返回最小值或最大值 |
| inrange,nerurange | 比较范围 |
| samevalue | 近似平等检查 |
| 功率,intpower,nroot,ldexp,exp | 指数函数 |
| LN,LNXP1,LOG2,LOG10,LOGN | 对数函数 |
| 罪,cos,sincos,棕褐色 | 三角函数 |
| Arcsin,Arccos,Arctan,Arctan2 | 反三角函数 |
| Sinh,Cosh,Sincosh,Tanh | 双曲线功能 |
| Arcsinh,Arccosh,Arctanh | 逆双曲函数 |
| Cotan,Cot,Secant,Sec,Cosecant,CSC | 相互三角函数 |
| Coth,Sech,Csch | 相互双曲线功能 |
| Arccot,arcsec,arccsc | 相互逆三角函数 |
| Arccoth,Arcsech,Arccsch | 相互逆双曲函数 |
| radtodeg,radtograd,radtocycle | 从弧度转换 |
| degtorad,Degtograd,degtocycle | 转换为学位 |
| Gradtorad,Gradtodeg,Gradtocycle | 从毕业生转换 |
| 环源性,环发行,环胎 | 从周期转换 |
证明高精度数学的一种有趣方法是计算Mandelbrot分形。当您放大分形时,您需要越来越精确。样品子目录包含一个firemonkey应用程序,该应用程序以4个级别的精度( Single , Double , DoubleDouble和QuadDouble )生成mandelbrot分形。
以下图像显示了分形的一小部分,使用1倍的倍倍(10 15 ,又称欧洲的一个台球)和Double精度:
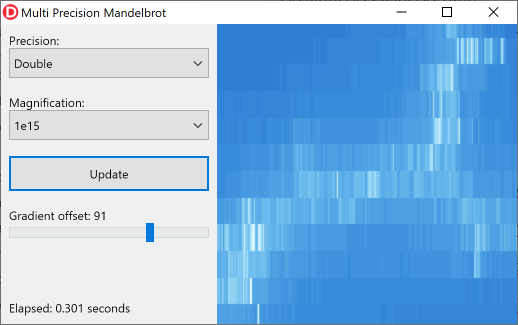
您可以清楚地看到, Double类型在此放大级别上不能提供足够的精度。 DoubleDouble类型提供了足够的精度:
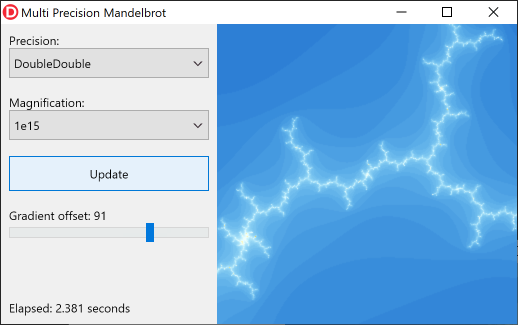
直到您达到10 31的放大率,您才需要切换到QuadDouble 。
neslib。多重分配要比上述更大。有关更多详细信息,您可以查看已记录的Neslib.MultiPrecision.pas源文件。可以在Unitests子目录和Mandelbrot样本应用程序中找到其他用法样本。
如果您对这些类型的技术细节和算法感兴趣,可以查看C子目录中的QD.pdf文件。
如上所述,该库建在QD库的顶部。这是一个C/C ++库,使用对象文件或静态库链接到您的Delphi可执行文件中。如果您自己需要或想自己构建这些对象文件和静态库,请查看C子目录中的readme.txt文件以获取说明。
Neslib.MultipRecision已根据简化的BSD许可获得许可。有关详细信息,请参见License.txt。
底层QD库是根据BSD-LBNL许可证获得许可的。有关详细信息,请参见C子目录中的文档BSD-LBNL-LICENSE.DOC。