Unduhan Neslib.MultiPrecision - Neslib.MultiPrecision download kode sumber

Neslib.MultiPrecision

Kode sumber Delphi

1.0.0

Unduh

Neslib.multiprecision

Jenis poin floating presisi tinggi untuk Delphi

Neslib.multiprecision menambahkan dua jenis titik mengambang tambahan untuk digunakan dengan Delphi. Ini menawarkan ketepatan yang hingga 4 kali lebih besar dari jenis Double .

Neslib.multiprecision dibangun di atas QD 2.3.22 dan bekerja di:

Windows (32-bit dan 64-bit)
MacOS (64-bit)
iOS (64-bit, tanpa simulator)
Android (32-bit dan 64-bit)

Algoritma yang digunakan untuk jenis ini dikembangkan oleh David H. Bailey, Yozo Hida dan Xiaoye S. Li. Lihatlah file QD.pdf di subdirektori C jika Anda tertarik dengan detailnya.

Instalasi

Untuk menginstal:

 > git clone https://github.com/neslib/Neslib.MultiPrecision

Perpustakaan ini tidak memiliki ketergantungan di perpustakaan lain. Juga tidak ada dependensi run-time. Perpustakaan C/C ++ QD yang mendasari ditautkan ke yang dapat dieksekusi menggunakan file objek atau pustaka statis.

Dua jenis titik mengambang baru

Perpustakaan ini mendefinisikan dua jenis titik mengambang tambahan:

DoubleDouble : Ini adalah tipe 128-bit yang memiliki dua kali presisi dari tipe Double .
QuadDouble : Ini adalah tipe 256-bit yang memiliki empat kali ketepatan tipe Double .

Kedua jenis memiliki kisaran yang sama dengan tipe ganda (sekitar ± 10 ³⁰⁸ ) tetapi presisi yang jauh lebih tinggi. Dibandingkan dengan Single dan Double :

Jenis	Eksponen Bit	Mantissa Bit	Presisi (Digit Desimal)
Lajang	9	24	7
Dobel	12	53	16
Doubledouble	12	106	32
Quaddouble	12	212	64

Nama -nama DoubleDouble dan QuadDouble berasal dari perpustakaan QD yang mendasarinya. Saya menganggap penamaan Float128 dan Float256 ini sebagai gantinya, tetapi sudah ada spesifikasi IEEE resmi untuk jenis (perangkat keras) tersebut. Dan karena ini tidak kompatibel dengan DoubleDouble dan QuadDouble , saya tidak ingin menambahkan kebingungan.

Perpustakaan QD yang mendasari tidak menggunakan emulasi untuk perhitungan. Sebaliknya, ia menggunakan kemampuan titik mengambang yang ada dari CPU untuk menggunakan 2 atau 4 nilai Double untuk meningkatkan presisi. Akibatnya, tipe ini jauh lebih cepat daripada perpustakaan matematika sewenang -wenang/presisi tinggi lainnya menggunakan presisi yang sama. Juga, sebagai lawan dari banyak perpustakaan lain, jenis ini tidak memerlukan alokasi memori dinamis, yang selanjutnya membantu kinerja dan juga mengurangi fragmentasi memori.

Penggunaan

Jenis DoubleDouble dan QuadDouble dapat digunakan dengan cara yang sama seperti tipe Double . Mereka mendukung operator yang biasa ( + , - , * , / , = , <> , < , <= , > dan >= ) serta sebagian besar metode yang tersedia untuk pembantu rekaman untuk tipe Double ( IsNan , IsInfinity , IsNegativeInfinity , IsPositiveInfinity , ToString , Parse dan TryParse ). Ada metode dan operator untuk dikonversi ke dan dari Double , DoubleDouble , QuadDouble dan String .

Karena bahasa Delphi tidak memungkinkan Anda untuk memasukkan literal floating-point presisi tinggi dalam kode sumber, nilai variabel DoubleDouble atau QuadDouble harus diinisialisasi dengan cara lain. Ada berbagai opsi (dengan asumsi DD adalah tipe DoubleDouble di sini):

Gunakan salah satu Init overloads. Misalnya, DD.Init(1.23); untuk menginisialisasi DoubleDouble dari Double .
Gunakan gips eksplisit, seperti pada DD := DoubleDouble(1.23); .
Gunakan salah satu konstanta yang telah ditentukan, seperti pada DD := DoubleDouble.Pi; .
Atau mungkin cara termudah adalah dengan hanya menetapkan nilai string, seperti dalam DD := '3.1415926535897932384626433832795'; .

Saya tidak menambahkan operator implisit , seperti DD := 1.23; , karena itu dapat menyebabkan konversi yang tidak disengaja yang berdampak pada kinerja.

Penting bagi Anda untuk memanggil MultiPrecisionInit sebelum melakukan perhitungan DoubleDouble / QuadDouble . Ini mempersiapkan FPU/CPU untuk matematika presisi tinggi. Anda dapat menggunakan MultiPrecisionReset untuk mengembalikan FPU/CPU ke keadaan sebelumnya.

Kustomisasi

Konfigurasi default perpustakaan cocok untuk sebagian besar aplikasi. Konfigurasi ini mengorbankan sedikit akurasi untuk meningkatkan kecepatan. Jika akurasi lebih penting daripada kecepatan untuk tujuan Anda, maka Anda dapat mengkompilasi perpustakaan dengan definisi MP_ACCURATE . Ini akan membuat banyak perhitungan sedikit lebih lambat tetapi lebih akurat.

Fungsi Matematika

Perpustakaan QD yang mendasari (dan dengan demikian perpustakaan ini) mendukung berbagai fungsi matematika yang umum. Selain itu, perpustakaan neslib.multiprecision menambahkan banyak ekuivalen fungsi yang ditemukan di sistem System.sysutils dan System.math.

Nama	Keterangan
Strtodoubledouble, strtoquaddouble, Strtodoublobledef, strtoquaddoubledef, Trystrtofloat	Konversi dari string
Floattostr, floattostrf	Konversi ke String
Terbalik	Hitung timbal balik
Rem	Hitung sisa, berbulat ke terdekat
Divrem	Hitung hasil pembagian, termasuk sisa
Fmod	Hitung sisa, bulat menuju nol
SQRT, SQR	Akar kuadrat dan persegi
Trunc, lantai, langit -langit, bulat	Berbagai metode pembulatan
Abs	Nilai absolut
Min, Max	Mengembalikan nilai minimum atau maksimum
Inrange, Ensurerange	Bandingkan dengan rentang
Samevalue	Perkiraan pemeriksaan kesetaraan
Daya, intpower, nroot, ldexp, exp	Fungsi eksponensial
LN, LNXP1, LOG2, LOG10, LOGN	Fungsi Logaritmik
Dosa, cos, sincos, tan	Fungsi trigonometri
Arcsin, Arccos, Arctan, Arctan2	Fungsi trigonometri terbalik
Sinh, cosh, Sincosh, Tanh	Fungsi hiperbolik
Arcsinh, Arccosh, Arctanh	Fungsi hiperbolik terbalik
Cotan, cot, secant, sec, cosecant, csc	Fungsi trigonometri timbal balik
Coth, sech, csch	Fungsi hiperbolik timbal balik
ARCCOT, ARCSEC, ARCCSC	Fungsi trigonometri terbalik timbal balik
Arccoth, Arcsech, Arccsch	Fungsi hiperbolik terbalik timbal balik
Radtodeg, Radtograd, Radtocycle	Konversi dari radian
Degtorad, degtograd, degtocycle	Konversi dari derajat
Gradtorad, Gradtodeg, GradTocycle	Konversi dari lulusan
Cycletorad, cycletodeg, cycletograd	Konversi dari siklus

Sampel

Cara yang menyenangkan untuk menunjukkan matematika presisi tinggi adalah dengan menghitung fraktal mandelbrot. Saat Anda memperbesar fraktal, Anda membutuhkan lebih banyak dan lebih presisi. Subdirektori sampel berisi aplikasi firemonkey yang menghasilkan fraktal mandelbrot pada 4 tingkat presisi ( Single , Double , DoubleDouble dan QuadDouble ).

Gambar berikut menunjukkan bagian kecil fraktal menggunakan pembesaran satu kuadrillion (10 ¹⁵ , alias satu biliar di Eropa) dan presisi Double :

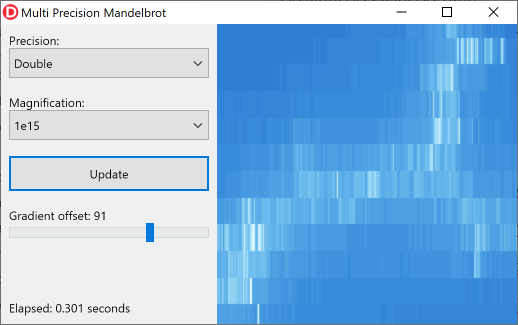
Anda dapat dengan jelas melihat bahwa tipe Double tidak memberikan presisi yang cukup pada tingkat pembesaran ini. Jenis DoubleDouble menawarkan lebih dari cukup presisi:

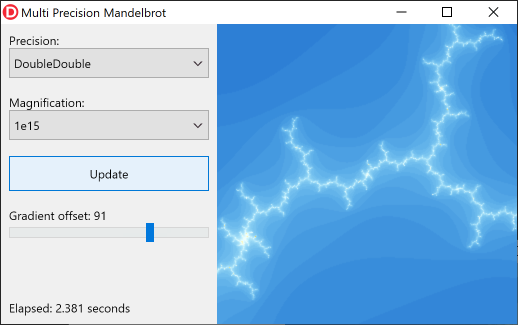
Tidak sampai Anda mencapai tingkat pembesaran 10 ³¹ , Anda perlu beralih ke QuadDouble .

Informasi lebih lanjut

Ada lebih banyak neslib.multiprecision daripada yang dijelaskan di atas. Untuk detail lebih lanjut Anda dapat melihat file sumber Neslib.MultiPrecision.pas yang terdokumentasi dengan baik. Sampel penggunaan tambahan dapat ditemukan di subdirektori Unittests dan aplikasi sampel Mandelbrot.

Jika Anda tertarik dengan detail teknis dan algoritma yang digunakan untuk jenis ini, Anda dapat melihat file QD.pdf di subdirektori C.

Membangun Perpustakaan C/C ++

Seperti yang dikatakan, perpustakaan ini dibangun di atas perpustakaan QD. Ini adalah pustaka C/C ++ yang ditautkan ke Delphi Anda yang dapat dieksekusi menggunakan file objek atau pustaka statis. Jika Anda membutuhkan atau ingin membuat file objek ini dan perpustakaan statis sendiri, maka lihatlah file readme.txt di subdirektori C untuk instruksi.